Учебное пособие
"Моделирование электрических цепей в системе
MathCAD
"
Введение
Большинство проблем, связанных с анализом схем электрических цепей, решается в два этапа. Первый этап заключается в составлении уравнений электрической цепи в форме, позволяющей использовать законы Кирхгофа и характеристики элементов, входящих в схему. Полученные на этом этапе уравнения представляют математическую модель цепи. Второй этап заключается в решении этих уравнений путем подходящих аналитических или численных методов. При машинном анализе электрических схем оба этапа могут выполняться ЭВМ, а программу общего анализа часто называют машинной моделью.
В настоящее время имеется достаточно много пакетов программ (PSpice, ElectronicWorkbench, P-Cad) для решения электрических (электронных) схем.
Любая такая программа машинного анализа схем признает и допускает лишь базовый на6ор схемных элементов, для которых она была разработана.
Чем больший базовый набор допускает программа, тем более многофункциональной она становится.
В случае, если схема содержит элементы, не входящие в базовый набор, следует заменить каждый такой элемент некоторой «эквивалентной схемой» на основе базовых элементов. Это часто невозможно, однако, в большинстве практических случаев считается возможным заменить каждый не допускаемый элемент «почти эквивалентной схемой», называемой схемной моделью. При разработке схемной модели необходимо, чтобы она имела такое же количество полюсов, что и рассматриваемый элемент, состояла лишь из элементов, входящих в базовый набор, чтобы результирующая схема аппроксимировала характеристики соответствующего элемента с переменной точностью.
Выбор наиболее подходящей модели зависит от ее правильного соответствия режима работы цепи: динамическому переходному режиму, установившемуся синусоидальному режиму или режиму постоянного тока.
Для синтеза нелинейных моделей по переменному току возможны два подхода, которые качественно согласуются с режимом работы реальных элементов: это физический метод и метод «черного ящика».
В физическом методе делается попытка преобразовать физическую структуру и механизм работы данного прибора (элемента) в схемную модель.
Реклама

В методе «черного ящика» полная характеристика схемной модели и моделируемого элемента, полученная экспериментально, должны совпадать с заданной степенью точности. При этом сначала строится статическая модель, а затем для построения модели по переменному току к ней добавляются паразитные ёмкости и индуктивности в существенно важных местах и нет необходимости понимать внутренний физический механизм работы прибора.
Успешное моделирование элементов цепи и создание их схемных моделей позволяет разработать электрическую схему, состоящую только из базовых элементов, которая используется при формировании математической модели (системы уравнений, адекватно описывающей процессы рассматриваемой цепи).
Использование пакета MathCAD в практикуме по решению задач электрических цепей позволяет при освоении курса разделить этапы формирования уравнений и численного их решения, избавляя от рутинных вычислений.
Самостоятельное формирование (моделирование) уравнений, основанных на топологии, способствует их успешному освоению, а возможность изменения численных методов их решения – подходящему их выбору.
Такой подход может быть плодотворным при освоении методов анализа электрических цепей и разработке новых.
1. Элементы теории матриц
1.1
Определение матрицы
Матрица
– это прямоугольная таблица чисел. Элемент с номерами ij
матрицы А,
а
ij
находится на пересечении i
-й строки и j
-го столбца:
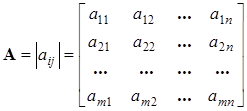 . (1.1) . (1.1)
Матрица размера (m
´n
) (или m
´n
– матрица) имеет m
строк и n
столбцов. У квадратной матрицы m
=
n
. Если а
ij
=0 при i
≠
j
, то квадратная матрица диагональная. Если в диагональной матрице все диагональные элементы равны 1, матрица называется единичной:
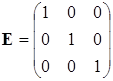 . (1.2) . (1.2)
Если у квадратной матрицы расположенные выше (ниже) главной диагонали элементы равны нулю, то матрица – нижне – (верхне-) треугольная:
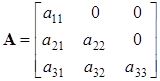 . (1.3) . (1.3)
Если у матрицы лишь один столбец или строка, в этом случае она называется столбцовой или строчной, или вектор-столбец, или вектор-строка, или просто вектор.
Вектор-столбец:
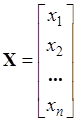 . (1.4) . (1.4)
Вектор-строка:
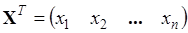 . (1.5) . (1.5)
Матрица А
Т
называется транспонированной к А
, если элемент а
ij
матрицы А
равен элементу а
ji
матрицы А
Т
для всех i
и j
Пример 1.1.
Если 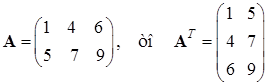 . .
Матрица А
называется симметричной, если А
=А
Т
, в противном случае – несимметричной.
При А
=-А
Т
– матрица кососимметричная.
1.2 Арифметические операции над матрицами
Реклама

1.2.1 Сложение
Сумма матриц А
и В
С = А + В
(1.6)
получается сложением каждого элемента матриц А
и В
одного размера m
´n
, т.е. 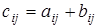 для всех i
и j
. для всех i
и j
.
Операция сложения матриц коммутативна
А + В = В + А
(1.7)
и ассоциативна
А + (В + С) = (А + В) + С,
(1.8)
а также
(А + В)Т
= АТ
+ ВТ
.
(1.9)
1.2.2 Умножение матриц
Произведение С = А
×
В
может быть получено тогда и только тогда, когда число столбцов матрицы А
равно числу строк матрицы В
.
Если А
размера m
´t
и В
размера t
´n
, то матрица С = А
×
В
определяется формулой
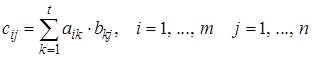 . (1.10) . (1.10)
Заметим, что в общем случае А
×
В ≠ В
×
А
.
Если А
×
В=В
×
А
, то матрицы коммутирующие или перестановочные.
Умножение обладает свойствами:
А
×
(В
×
С) = (А
×
В)
×
С
(1.11)
ассоциативности и
(А+В)
×
С=А
×
С+В
×
С и А
×
(В+С)=А
×
В+А
×
С
(1.12)
дистрибутивности.
1.2.3 Умножение на скаляр
Умножение матрицы (А)
на скаляр b
означает, что каждый элемент матрицы умножается на скаляр
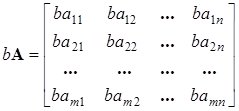 (1.13) (1.13)
1.2.4. Вычисление определителей
Пусть А
– квадратная матрица порядка n
, n
>
1:
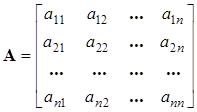 . .
Определителем квадратной матрицы А
порядка n
,
n
>1 называется число
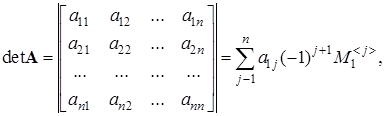
где 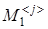 – определитель квадратной матрицы порядка n
-1, полученной из матрицы А
вычеркиванием первой строки и j
-того столбца. – определитель квадратной матрицы порядка n
-1, полученной из матрицы А
вычеркиванием первой строки и j
-того столбца.
Формулу 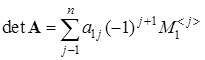 называют формулой вычисления определителя разложением по первой строке
. Число называют формулой вычисления определителя разложением по первой строке
. Число 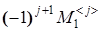 называется алгебраическим дополнением элемента a
1
j
. называется алгебраическим дополнением элемента a
1
j
.
1.2.5 Обращение матрицы
Если А
и В-
две квадратные матрицы порядка n
, такие, что
А
×
В=Е,
(1.14)
то говорят, что В
-матрица, обратная к А,
и обозначается через
В=А
-1
,(1.15)
заметим, что А
×
А-
1
=А-
1
×
А=Е,
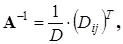 (1.16) (1.16)
где D
=detА
(определитель матрицы А
); 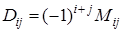 – алгебраическое дополнение элемента а
ij
.
, а Мij
минор к элементу aij
(определитель, полученный из А
удалением i-й строки и j-ого столбца. – алгебраическое дополнение элемента а
ij
.
, а Мij
минор к элементу aij
(определитель, полученный из А
удалением i-й строки и j-ого столбца.
Обращение обладает свойствами:
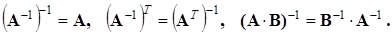 (1.17) (1.17)
А
-1
существует, если detA
¹0.
Если detA
=0, то матрица особенная.
1.3 Матричное представление линейных уравнений
Система линейных уравнений может быть записана в виде матричного уравнения:
А
×
Х=В
. (1.18)
Ее решение получаем, умножая обе части равенства слева на А
-1
:
А
-1
×А
×
Х
=1×Х
=А
-1
×В
,
то есть:
Х
=А
-1
×В
. (1.19)
Это удобный способ выразить решение Х
, но существуют методы решения значительно лучше, чем явное формирование матрицы А
-1
и умножение ее на В
.
1.4 Используемые инструменты
MathCAD
Большинство вычислений с матрицами, как и другие вычисления в Mathcad, можно выполнить тремя способами: с помощью панелей инструментов, выбором операции в меню или обращением к соответствующей функции.
Панель операций с матрицами и векторами в Matrix
открывается щелчком по кнопке  в панели математических инструментов. За кнопками панели закреплены следующие функции: в панели математических инструментов. За кнопками панели закреплены следующие функции:
 – определение размеров матрицы; – определение размеров матрицы;
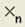 – ввод нижнего индекса; – ввод нижнего индекса;
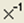 – вычисление обратной матрицы; – вычисление обратной матрицы;
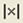 – вычисление определителя матрицы: – вычисление определителя матрицы: 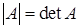 ; ;
вычисление длины вектора |х
|, |х
|2
=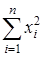 ; ;
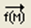 – поэлементные операции с матрицами: если А
={а
ij
}, B
={bij
}, то – поэлементные операции с матрицами: если А
={а
ij
}, B
={bij
}, то 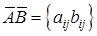 ; ;
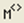 – определение столбца матрицы: М
<
j
>
– j
-й столбец матрицы; – определение столбца матрицы: М
<
j
>
– j
-й столбец матрицы;
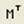 – транспонирование матрицы: М
={mij
}, MT
={mji
}, – транспонирование матрицы: М
={mij
}, MT
={mji
},
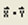 – вычисление скалярного произведения векторов: – вычисление скалярного произведения векторов: 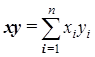 ; ;
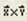 – вычисление векторного произведения двух векторов: a
´b
=(a
2
b
2
– a
3
b
2
–a
2
b
1
–a
1
b
2
–a
2
b
1
); – вычисление векторного произведения двух векторов: a
´b
=(a
2
b
2
– a
3
b
2
–a
2
b
1
–a
1
b
2
–a
2
b
1
);
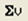 – вычисление суммы компонент вектора: – вычисление суммы компонент вектора: 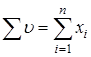 ; ;
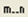 – определение диапазона изменения индекса переменной; – определение диапазона изменения индекса переменной;
 – визуализация цифровой информации, сохраненной в матрице. – визуализация цифровой информации, сохраненной в матрице.
Для того, чтобы выполнить какую-либо операцию с помощью панели инструментов, нужно выделить матрицу и щелкнуть в панели по кнопке операции либо щелкнуть по кнопке в панели и ввести в помеченной позиции для матрицы.
Функции определения матриц и операции с блоками матриц:
matrix
(
m
,
n
,
f
)
– создает и заполняет матрицу размерности m´n, элемент которой, расположенный в i
-й строке, j
-м столбце, равен значению f
(
i
,
j
)
функции f
(
x
,
y
)
;
diag
(
v
)
– создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v
;
identity
(
n
)
– создает единичную матрицу порядка n;
augment
(
A
,
B
)
– формирует матрицу, в первых столбцах которой содержится матрица А
, а в последних – матрица В
(матрицы А
и В
должны иметь одинаковое число строк);
sta
с
k
(А, В)
– формирует матрицу, в первых строках которой содержится матрица А
, а в последних – матрица В
(матрицы А
и В
должны иметь одинаковое число столбцов);
submatrix
(
A
,
ir
,
jr
,
ic
,
jc
)
– формирует матрицу, которая является блоком матрицы А
, расположенным в строках с ir
по jr
и в столбцах с ic
по jc
,
ir
£
jr
, ic
£
jc
.
Номер первой строки (столбца) матрицы или первой компоненты вектора хранится в Mathcad в переменной ORIGIN. По умолчанию в Mathcad координаты векторов, столбцы и строки матрицы нумеруются, начиная с 0 (ORIGIN=0). Поскольку в математической записи чаще используется нумерация с 1, здесь и в дальнейшем перед началом работы с матрицами будем определять значение переменной ORIGIN равным 1, т.е. будем прежде всего выполнять команду ORIGIN=1.
Функции вычисления числовых характеристик матриц:
last
(
v
)
– вычисление номера последней компоненты вектора v
;
legth
(
v
)
– вычисление количества компонент вектора v
;
rows
(
A
)
– вычисление числа строк в матрице А
;
cols
(
A
)
– вычисление числа столбцов в матрице А
;
max
(
A
)
– вычисление наибольшего элемента в матрице А
;
min
(
A
)
– вычисление наименьшего элемента в матрице А
;
tr
(
A
)
– вычисление следа квадратной матрицы А
*
;
rank
(
A
)
– вычисление ранга матрицы А
;
norm
1 (
A
),
norm
2 (
A
),
norme
(
A
),
normi
(
A
)
– вычисление норм квадратной матрицы А
.
Функции, реализующие численные алгоритмы решения задач линейной алгебры:
rref
(
A
)
– приведение матрицы к ступенчатому виду с единичным базисным минором (выполняет элементарные операции со строками матрицы);
eigenvals
(
A
)
– вычисление собственных значений квадратной матрицы А
;
eigenvecs
(
A
)
– вычисление собственных векторов квадратной матрицы А
; значением функции является матрица, столбцы которой есть собственные векторы матрицы А
, порядок следования которых отвечает порядку следования собственных значений, вычисленных функцией eigenvals
(
A
);
eigenvec
(
A
,
l
)
– вычисление собственного вектора матрицы А
, отвечающего собственному значению l;
lsolve
(
A
,
b
)
– решение системы линейных уравнений Ax
=
b
.
Задание 1.
Определить матрицу А
размером 3´3 с помощью панели Matrix и трансформировать ее.
Создать матрицу В
размером 3´3 с помощью функции Matrix.
Вычислить суммы А+В
и В+А
, произведения АВ
и ВА
, исследовать матрицы на симметричность.
Задать единичную матрицу Е
3-го порядка, вычислить произведения ЕА
и АЕ
.
Сформировать вектор v
, представляющий 2-й столбец матрицы А,
и диагональную матрицу diag
(
v
).
Определить матрицы С
иD
, используя функции augment
(
A
,
V
)
и sta
с
k
(
A
,
VT
).
Решить систему АХ=
V
, используя обратную матрицу А
-1
и функцию isolve
(
A
,
b
).
2. Основные элементы схемы и понятия
2.1 Двухполюсные пассивные элементы
Основными пассивными (двухполюсными) элементами схемы являются сосредоточенные, не зависящие от времени резисторы, индуктивности и емкости.
Резистором
называют элемент, для которого текущий ток i
и приложенное напряжение u
связаны законом Ома:
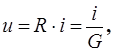 (2.1) (2.1)
где R
– сопротивление резистора, измеряемое в Омах (Ом), а G
– проводимость, измеряемая в Сименсах (См). Напряжение u
измеряется в Вольтах (В), а ток i
в Амперах (А).
Положительное направление показано на рис. 2.1:
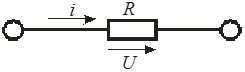
Рис. 2.1
Индуктивность
обозначается L
и измеряется в Генри (Гн):
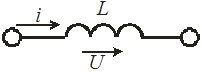
Рис. 2.2
Для линейной индуктивности напряжение и ток связаны соотношением
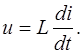 (2.2) (2.2)
Емкость обозначается с
и измеряется в Фарадах (Ф):
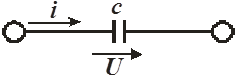
Рис. 2.3
Напряжение и ток в емкости описываются уравнением
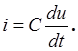 (2.3) (2.3)
Соотношения (2.1), (2.2), (2.3) определяют характеристики компонент (схемы), их называют компонентными уравнениями.
Следует заметить, что дифференциальные соотношения (2.2), (2.3) между токами и напряжениями на индуктивности и емкости преобразованием Лапласа преобразуются в алгебраические:
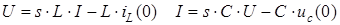 . .
Начальные значения токов в индуктивностях и напряжений на емкостях учитываются дополнительными источниками.
Индуктивные и емкостные сопротивления определяются следующим образом:
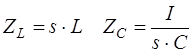 . (2.4) . (2.4)
Для расчета установившегося режима в линейных цепях при синусоидальном воздействии полагаем S
=
jω
и пренебрегаем начальными токами iL
(0+)=0 и напряжениями uc
(0+)=0.
2.2 Независимые источники
Независимый источник напряжения (ЭДС) обеспечивает заданное значение напряжения на его полюсах независимо от того, какой ток течет через него (рис 2.4):
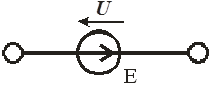
Рис. 2.4
Независимый источник тока создает заданный ток, а напряжение на его полюсах зависит от цепи, подключенной к источнику (рис 2.5):
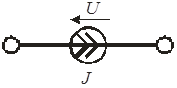
Рис. 2.5
2.3 Схемы замещения реальных источников
Независимые источники идеальны и физически нереализуемы. Однако они могут быть использованы для моделирования реальных источников при добавлении других идеальных элементов. Одна из моделей источника напряжений, показанная на рис. 2.6, а, называется схемой Тавенена. Здесь Zb
моделирует внутреннее сопротивление источника (U
=
E
при I
=0,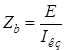 ,
гдеI
кз
- ток при U
=0). ,
гдеI
кз
- ток при U
=0).
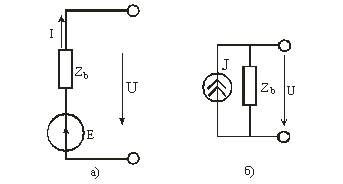
Рис. 2.6
Модель реального источника на рис. 2.6, б, где сопротивление Zb
включен параллельно идеальному источнику тока, называется схемой Нортона, а 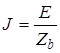 – ток источника тока. – ток источника тока.
2.4 Зависимые источники
1. Источник напряжения, управляемый напряжением или идеальный усилитель (ИНУН). Уравнения этого четырехполюсника:
i
1
=0 u
2
=
Ku
×
u
1
,
где К
u
– коэффициент передачи по напряжению
В матричной форме:
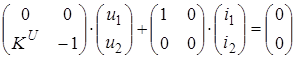 (2.5) (2.5)
На рис. 2.7 приведена схема ИНУН:
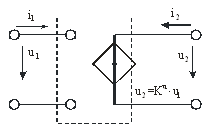
Рис. 2.7.
2. Источник тока, управляемый напряжением (ИТУН). Уравнения этого четырехполюсника:
i
1
=0 i
2
=
g
×
u
1
,
где g
– передаточная проводимость.
В матричной форме:
 . (2.6) . (2.6)
Его схема приведена на рис. 2.8:
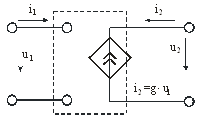
Рис. 2.8.
3. Источник напряжения, управляемый током (ИНУТ). Его уравнения:
u
1
=0 u
2
=
r
×
i
1
или
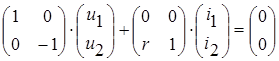 , (2.7) , (2.7)
где r
–
передаточное сопротивление.
На рис. 2.9 приведена схема ИНУТ:
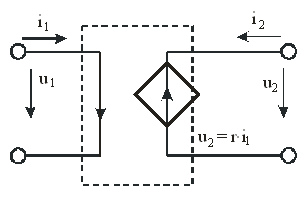
Рис. 2.9.
4. Источник тока, управляемый током (ИТУТ) или идеальный усилитель тока (рис. 2.10). Его уравнения:
u
1
=
0 i
2
= К
i
i
1
или
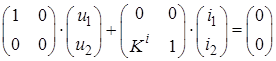 , (2.8) , (2.8)
где К
i
– коэффициент передачи по току.
На рис. 2.10 приведена схема ИТУТ:

Рис. 2.10
2.5 Элементарные четырехполюсники
1. Идеальный трансформатор определяется с помощью уравнений
U
1
=
±
n
×
U
2
, I
1
=
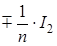
или
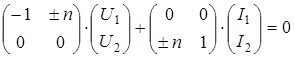 (2.9) (2.9)
На рис. 2.11 приведена схема трансформатора (а) и его эквивалентная схема (б):
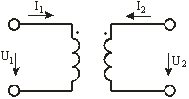 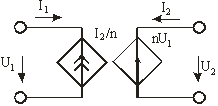
(а) Рис. 2.11 (б)
Гиратор определяется как четырехполюсник, для которого справедливы уравнения:
I
1
=-
g
2
×
U
2
I
2
=
g
1
×
U
1
.
(2.10)
Гиратор можно представить с помощью двух ИТУН (рис. 2.12):

Рис. 2.12
Если постоянные гирации равны, т.е. g
1
=
g
2
=
g
, то гиратор называется идеальным. Уравнения (2.10) можно переписать в форме:
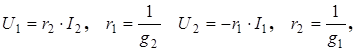 (2.11) (2.11)
а схема гиратора приведена на рис. 2.13:
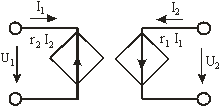
Рис. 2.13.
2.6 Операционный усилитель
К активным многополюсникам относится операционный усилитель (ОУ), имеющий дифференциальный вход с очень большим входным сопротивлением, малое выходное сопротивление и высокий коэффициент усиления. Условное обозначение ОУ и его схема замещения приведены на рис. 2.14:
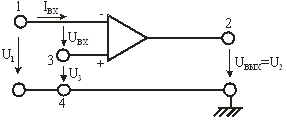

Рис. 2.14.
2.7 Законы электрических цепей
Ток 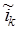 и напряжение и напряжение 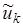 относятся к некоторой обобщенной
k
-ой ветви, содержащей источник тока и источник ЭДС
(рис. 2.15): относятся к некоторой обобщенной
k
-ой ветви, содержащей источник тока и источник ЭДС
(рис. 2.15):
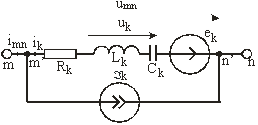
Рис. 2.15.
Согласно первому закону Кирхгофа применительно к узлу m
’ (или n
’) на рисунке, имеем:
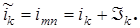 (2.12)
(2.12)
Согласно второму закону Кирхгофа для контура, проходящего по проводникам ветви k
от узла m
к n
, и по внешнему пространству – от узла n
к m
, имеем:
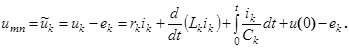 (2.13) (2.13)
Последние выражения связывают токи и напряжения в обобщенных ветвях графа, изображаемых в графе схемы отрезками, с токами и напряжениями ветвей и источниками тока и ЭДС, когда таковые содержатся в исходной схеме.
При записи уравнений, согласно законам Кирхгофа для графа схемы будем иметь в виду, что в эти уравнения войдут токи и напряжения обобщенных ветвей схемы цепи. Следовательно, для графа схемы можно написать:
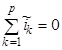 и и 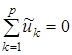 или или 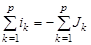 и и 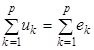 . (2.14) . (2.14)
В случае установившихся процессов мгновенные значения токов и напряжений заменяются их комплексными действующими значениями, при применении преобразования Лапласа их операторными изображениями (хотя в последнем случае необходимо начальные условия токов на индуктивностях и напряжения на емкостях учитывать дополнительными источниками), и в этом случае уравнения (2.14) принимают вид:
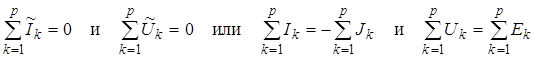 .(2.14а) .(2.14а)
2.8 Функции цепи. Полюсы и нули
Функции цепи определяются для схем, не имеющих начальных напряжений на емкостях и токов в индуктивностях.
Используя символические выражения ZL
=
s
×
L
,
YC
=s×C
и допуская, что существует единственный источник, определяем функции цепи следующим образом:
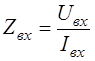 – входное сопротивление; (2.15) – входное сопротивление; (2.15)
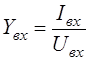 – входная проводимость; (2.16) – входная проводимость; (2.16)
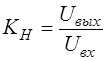 – коэффициент передачи по напряжению; (2.17) – коэффициент передачи по напряжению; (2.17)
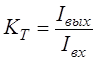 – коэффициент передачи по току; (2.18) – коэффициент передачи по току; (2.18)
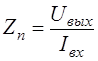 – передаточное сопротивление; (2.19) – передаточное сопротивление; (2.19)
 – передаточная проводимость. (2.20) – передаточная проводимость. (2.20)
Если цепь состоит из сосредоточенных элементов, то все функции цепи представляют собой рациональные функции от S
:
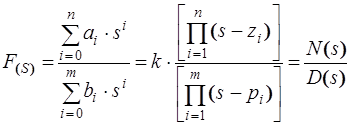 . (2.21) . (2.21)
Полином в числителе имеет n
корней zi
, называемых нулями, а полином в знаменателе – m
корней р
i
,
называемых полюсами.
С точностью до постоянного множителя k
расположение нулей и полюсов на комплексной плоскости полностью определяет свойства функции цепи.
Отклик линейной схемы на синусоидальное воздействие можно рассчитать, положив в выражении для функции цепи S
=
j
w
, тогда
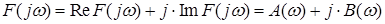 , (2.22) , (2.22)
где А(ω)
– четная, а В(ω)
– нечетная функции ω
.
Модуль функции F
:
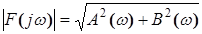 . (2.23) . (2.23)
Фазовый сдвиг определяется по формуле:
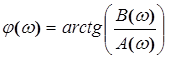 . (2.24) . (2.24)
Выражение (2.22) можно записать в виде
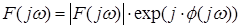 . (2.25) . (2.25)
Когда частоту w
рассматривают, как независимую переменную, 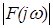 и f
(
w
)
называют амплитудной и фазовой характеристиками цепи. и f
(
w
)
называют амплитудной и фазовой характеристиками цепи.
Групповая задержка определяется следующим образом:
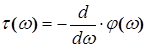 . (2.26) . (2.26)
3. Формирование уравнений цепи на основе теории графов
3.1 Граф схемы и некоторые его подграфы
При разработке машинных методов анализа электрических цепей можно определить некоторые их свойства, рассматривая только структуры цепи. Теория графов является для этого удобным средством.
Для описания топологии (структуры) цепи заменим каждую ветвь схемы отрезком линии, называемым ветвью графа, а узлы точками – узлами (вершинами) графа.
Эта совокупность ветвей и узлов, представляющая топологию цепи, называется графом.
Графы называют изоморфными, если их топологические свойства одинаковы.
Графы, у которых все ветви ориентированы, называют ориентированными. В противном случае граф считают неориентированным. Планарным называют граф, который в результате изоморфных преобразований может быть изображен на плоскости без пересечения ветвей. Планарной электрической схеме соответствует планарный граф. На рис. 3.1 показана схема электрической цепи (а) и ее ориентированный граф (б):
 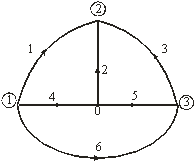
(а) (б)
Рис. 3.1
Подграфом графа называют часть графа. Подграфом может быть одна ветвь, узел или множество ветвей и узлов, содержащееся в данном графе.
Путь – упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются в этом пути только один раз (4–2–3).
Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути (1–2–4). На рис. 3.1 один из контуров содержит ветви 1, 2, 4.
Если между любой парой узлов графа существует путь, то граф называют связным.
Деревом связного графа называют связный подграф, содержащий все узлы графа, но не содержащий ни одного контура.
Примеры деревьев графа на рис. 3.1, б приведены на рис. 3.2:
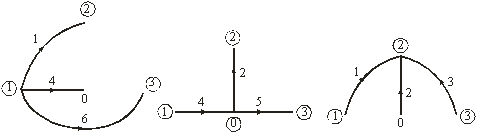
Рис. 3.2
Ветви графа, которые дополняют дерево до исходного графа, называют ветвями связи (хордами). Ветви графа, входящие в дерево, называют ребрами. Если граф содержит р
ветвей и q
узлов, то число ветвей любого дерева d
=
q
-
1, а число ветвей связи k
=
p
-
q
+
1.
Ветви связи деревьев графа на рис. 3.1, б приведены на рис. 3.3:
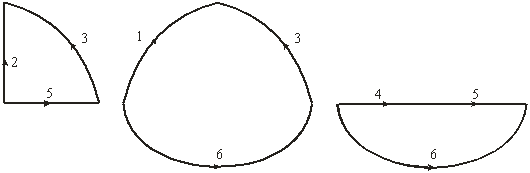
Рис. 3.3
Сечением графа называют множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых в частном случае может быть изолированным узлом.
Например, ветви графа 1–4–6, 3–2–4–6, 3–5–6 образуют сечения (рис. 3.4):
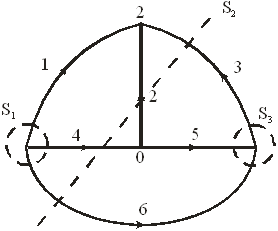
Рис. 3.4
Главным контуром называют контур, состоящий из ветвей дерева и только одной ветви связи. Другими словами, при соединении любой ветви связи с деревом образуется главный контур. Главным сечением считается сечение, состоящее из ветвей связи и только одной ветви дерева. Каждая ветвь дерева позволяет образовать одно сечение.
На рис. 3.5 показаны главные сечения, главные контуры для выделенного дерева графа (рис. 3.1, б):
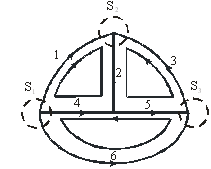
Рис. 3.5
3.2 Топологические матрицы графа
3.2.1 Матрица соединений
Матрица соединений (инциденций) А
– это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа (ЗКТ) для узлов.
Строки этой матрицы соответствуют узлам, столбцы – ветвям. Элементы а
ij
матрицы А
определяются следующим образом:
aij
=
1, если ветвь j
соединена с узлом i
и направлена от узла;
aij
=
-1, если ветвь j
соединена с узлом i
и направлена к узлу;
aij
=0, если ветвь j
не соединена с узлом i
.
Число строк матрицы А
равно числу независимых узлов g
=
q
-
1.
3.2.2 Матрица сечений
Матрица сечений D
– это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа (ЗКТ) для сечений. Строки матрицы D
соответствуют сечениям, столбцы – ветвям.
Элемент dij
матрицы D
=[dij
] определяется следующим образом:
dij
=1, если ветвь j
содержится в сечении i
и направлена согласно с направлением сечения;
dij
=-
1, если ветвь j
содержится в сечении i
и направлена противоположно направлению сечения;
dij
=
0, если ветвь j
не содержится в сечении i
.
Если матрица D
составлена для главных сечений, то ее называют матрицей главных сечений. При этом за положительное направление сечения обычно принимают направление ветви дерева данного сечения. Число строк матрицы D
равно числу независимых сечений g
.
Закон Кирхгофа для сечений в матричной форме записывают следующим образом (ЗКТ):
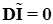 (3.3) (3.3)
Если матрицу напряжений ветвей дерева (ребер) обозначить через Ug
, то
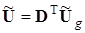 , (3.4)
, (3.4)
т.е. напряжения ветвей схемы, определяют через напряжения ветвей дерева (ребер).
Если ветвям дерева присвоены первые номера, то матрица главных сечений может быть разложена на две подматрицы:
D
=
[1
F
],
(3.5)
где 1
– единичная подматрица порядка q
-
1, столбцы которой соответствуют ребрам;
F
– подматрица, столбцы которой соответствуют ветвям связи (хордам).
3.2.3 Матрица контуров
Матрица контуров С
– это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа (ЗКН). Строки матрицы С
соответствуют контурам, столбцы – ветвям.
Элементы с
ij
матрицы С
=[с
ij
]
определяются следующим образом:
с
ij
=
1, если ветвь j
содержится в контуре i
и направление ветви совпадает с направлением обхода контура;
с
ij
=-1, если ветвь j
содержится в контуре i
и направление ветви противоположно направлению обхода контура;
с
ij
= 0, если ветвьj
не содержится в контуре i
.
Матрицу С
, записанную для главных контуров, называют матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура.
Второй закон Кирхгофа для напряжений в матричной форме записывают следующим образом (ЗКН):
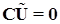 (3.6) (3.6)
Токи всех обобщенных ветвей могут быть выражены как линейные комбинации токов обобщенных ветвей связи (контурных токов)
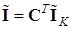 (3.7) (3.7)
где I
К
– столбовая матрица контурных токов.
Если ветвям дерева присвоены первые номера, то матрица главных контуров состоит из двух подматриц:
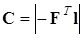 (3.8) (3.8)
гдеF
– подматрица матрицы сечений C
, составленная на основании того же самого дерева;
1
– единичная подматрица порядка k
=р-
q
+l.
Таким образом, в матричной форме могут быть записаны:
– первый закон Кирхгофа (ЗКТ):
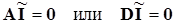 (3.9)
(3.9)
– второй закон Кирхгофа (ЗКН):
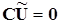
3.3 Полная система уравнений электрических цепей
Законы Кирхгофа применительно к графу схемы или электрической цепи характеризуют систему в целом без учета характеристик ее элементов. Матричные уравнения
Ai
=-
A
Á
(или Di
=-
D
Á
) и Cu
=
Ce
(3.10)
определяют систему из р
отдельных уравнений. Такая система недостаточна для описания процессов в электрических цепях, так как не известны р
токов и р
напряжений.
Чтобы дополнить систему уравнений, необходимо определить (или задать) еще р
уравнений. Эти уравнения должны отражать свойства элементов системы – ветвей электрической цепи. Очевидно, что такие связи должны быть записаны для р
ветвей цепи. В матричной форме запишем эти уравнения в виде
i
=
f
(
u
)
или u
=
j
(
i
),
т.е.
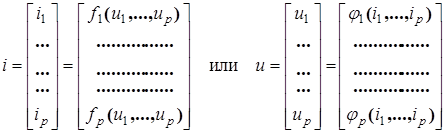 (3.11) (3.11)
В зависимости от характера функций fk
и j
k
(
k
=1…р)
системы уравнений электрических цепей могут быть линейными – для линейных электрических цепей, т.е. для цепей, у которых r
,
L
, С
и М
не зависят от значений и направлений токов и напряжений в цепи, и нелинейными – для нелинейных электрических цепей, т.е. для цепей, у которых r
,
L
, С
или М
хотя бы одного из участков зависят от значений или от направлений токов и напряжений в этом участке цепи.
Каждая ветвь линейной цепи может содержать сопротивление, индуктивность, емкость, идеальный источник ЭДС и идеальный источник тока (рис. 3.9).
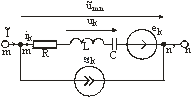
Рис. 3.9
Ток в сопротивлении ветви 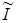 и падение напряжения ветви U
связаны законом Ома. и падение напряжения ветви U
связаны законом Ома.
U
=
Z
×
I
,
где сопротивление ветви 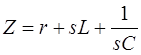 . Эти соотношения для всех ветвей можно записать в матричной форме: . Эти соотношения для всех ветвей можно записать в матричной форме:
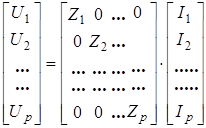
или кратко
U
=
Z
×
I
,
(3.12)
где Z
– диагональная матрица сопротивлений ветвей;
U
, I
, J
, E
– соответственно векторы напряжений и токов ветвей, токов источников тока и ЭДС ветвей.
Это матричная форма закона Ома.
Замечание
:
Матрица Z
диагональна лишь в случае, когда ток k
-ой ветви создает напряжение на сопротивлении Z
, k
-ой ветви. В цепях со взаимной индукцией Z
имеет элементы вне главной диагонали Zij
=
Zji
=
±
sMij
.
М
-сопротивления индуктивной связи i
-ой и j
-
ой ветвей. Они положительны (отрицательны), если ориентация i
-ой и j
-ой ветвей по отношению одноименных зажимов одинакова (противоположна).
Уравнения закона Ома можно представить в другой форме:
I
=
Y
×
U
,
(3.13)
где Y
=
Z
-
1
– матрица проводимостей, обратная матрице сопротивлений ветвей.
Если в функции fk
и j
k
входят производные токов и напряжений, то процессы в этой линейной или нелинейной электрической цепи будут характеризоваться системой, соответственно, линейных или нелинейных дифференциальных уравнений. При отсутствии производных в функциях fk
и j
k
процессы в этой линейной или нелинейной электрической цепи будут характеризоваться системой, соответственно, линейных или нелинейных алгебраических уравнений.
Система из 2 р
уравнений, включающая в себя уравнения, записанные согласно законам Кирхгофа, и уравнения, характеризующие связи между токами и напряжениями элементов электрической цепи, и есть полная система уравнений электрической цепи, или полная математическая модель этой цепи.
3.4 Узловые уравнения
Для формирования системы уравнений относительно узловых напряжений выразим 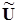 через параметры пассивных и активных элементов обобщенных ветвей: через параметры пассивных и активных элементов обобщенных ветвей:
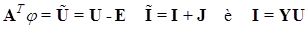 . .
Согласно первому закону Кирхгофа, для узлов графа
AI
=-
AJ
или AYU
=-
AJ
.
Теперь напряжение на ветвях определим через узловые потенциалы:
U
=
A
T
×
j
+Е
.
Таким образом, получаются уравнения
AY
×
A
T
×
j
=
AJ
-
AY
×
E
, (3.14)
которые называют узловыми уравнениями.
Если ввести обозначения
– Y
y
=
AY
×
AT
– матрица узловых проводимостей,
– J
y
=
AJ
-
AY
×
E
– матрица узловых токов,
то узловые уравнения запишутся кратко:
Yy
j
=
Jy
.
(3.14a)
При выполнении узлового анализа на ЭВМ обычно не строятся матрицы A
и Y
и не выполняют матричные умножения, а непосредственно пользуются правилами составления узловых уравнений:
1. Диагональные элементы матрицы Y
у
положительны и Yjj
равны сумме проводимостей ветвей, подключенных к j
-муузлу.
2. Внедиагональные элементы матрицы Yy
отрицательны и Yjk
равны сумме проводимостей ветвей, включенных между j
-м иk
-
м узлами.
3. Произвольный элемент вектора тока Jy
с номеромj
J
j
равны суммеузловых токов, втекающих в j
-
узел.
Тогда l-я ветвь, направленная от узла j
к узлу k
, приводит к следующему вкладу в матрицы Yy
и Jy
:
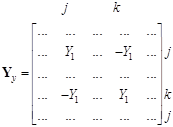 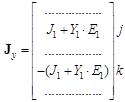
Так составляются уравнения по методу узловых потенциалов последовательным перебором топологического списка ветвей схемы.
Потенциалы узлов j
k
равны напряжениям Vk
между q
-1 узлом и опорным узлом.
3.5 Контурные уравнения
Уравнения на основе второго закона Кирхгофа
CU
=
CE
,
уравнение закона Ома
U
=
Z
×
I
и соотношение
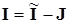
подставим в контурное уравнение и получим:
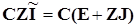 . .
Токи в обобщенных ветвях определим через контурные токи:
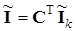 . .
Так получаются контурные уравнения:
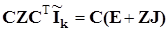 . (3.15) . (3.15)
Если ввести обозначения
Zk
=С
Z
×
С
T
– матрица контурных сопротивлений,
Ek
= С
E
-С
Z
×
J
– матрица контурных ЭДС, то контурные уравнения запишутся в виде:
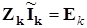 . (3.15а) . (3.15а)
В матричной форме решения для контурных токов
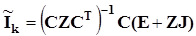 (3.16) (3.16)
выражают принцип наложения.
3.6 Независимые токи и напряжения
Запишем уравнения ЗКТ, используя матрицу главных сечений:
D
×
I
=0,
где I
– вектор токов ветвей.
Разделив матрицу на блоки, получим: 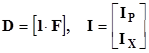
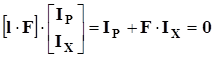
или
IP
= –
F
×
IX
.
(3.17)
Токи ребер графа выражаются через токи хорд:
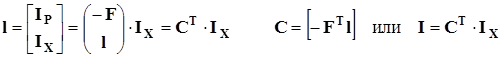 (3.17а) (3.17а)
Токи хорд можно рассматривать как независимые переменные.
Уравнения, составленные по ЗКН,
CU
=0
,
где U
– вектор напряжений на всех ветвях, использовав блочное представление матрицы С
, запишем:
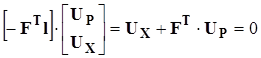 . .
Напряжение на ветвях хорд выражаются через напряжения на ветвях ребер:
UX
=
FT
×
UP
.
(3.18)
Напряжение на ветвях можно представить:
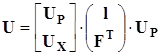 . .
Из последнего, с учетом D
=[
l
×
F
],
следует:
U
=
DT
×
UP
. (3.18а)
Напряжения, соответствующие ребрам графа, можно рассматривать как независимые переменные.
3.7 Типы ветвей
Y
-ветвью
называют ветвь, представленную проводимостью и описываемую компонентными уравнениями для токов. Ветвь включает проводимости, ветвь ИТУН, ветвь ИТУТ, независимые источники тока (рис. 3.10).
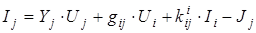 , ,
где  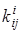 -
коэффициент передачи по току;
-
коэффициент передачи по току;
gij
– передаточная проводимость.
В матричной форме уравнения для Y ветвей:
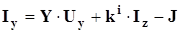 . (3.19) . (3.19)
В матрицу проводимостей Y
включены проводимости ветвей и и передаточные проводимости. К этим уравнениям присоединяются уравнения многополюсников в Y-форме.
IM
=
YM
×
UM
.
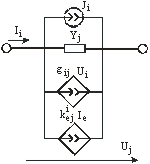
Рис. 3.10.
Z
-ветви
характеризуются сопротивлениями и описываются напряжениями.
Обобщенная 2-полюсная Z-ветвь показана на рис. 3.11:
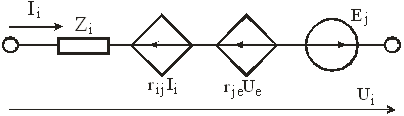
Рис. 3.11.
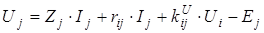 , ,
где rji
– передаточное сопротивление;
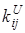 – коэффициент передачи по напряжению. – коэффициент передачи по напряжению.
Уравнение Z-ветвей в матричной форме имеет вид:
UZ
=Z
×
IZ
+KU
×
UY
-E.
(3.20)
В Z
матрицу входят сопротивления ветвей и передаточные сопротивления. Уравнения Z-ветвей дополняются уравнениями многополюсников в Z-форме.
UM
=
ZM
×
IM
Компонентные уравнения обобщенных ветвей:
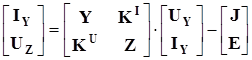 . (3.21) . (3.21)
3.8 Модифицированный метод узловых потенциалов
(Расширенное узловое уравнение)
В расширенном узловом уравнении переменными являются потенциалы узлов и токи Z-ветвей.
Компонентные уравнения, связывающие токи и напряжения Y- и Z-ветвей:
IY
=Y
×
UY
+KI
×
IZ
-J
UZ
=
Z
×
IZ
+
KU
×
UY
-
E
.
Если первые номера присваиваются Y-, а последующие Z-ветвям, то матрица соединений и вектор-столбец токов могут быть представлены двумя подматрицами:
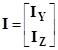 ; ; 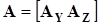 , ,
а уравнение по первому закону Кирхгофа примет вид:
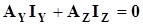 . (3.22) . (3.22)
Преобразуем это уравнение с учетом закона Ома для Y-ветвей:
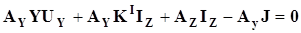 . .
Тогда, принимая во внимание 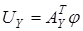 , получим: , получим:
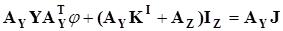 . (3.23) . (3.23)
Закон Ома для Z-ветвей:
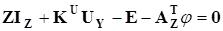
с учетом 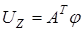 приводит к уравнению приводит к уравнению
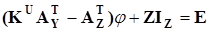 . (3.24) . (3.24)
Уравнения (3.23) и (3.24) объединяются в одно уравнение, получаем расширенное узловое уравнение (РУУ):
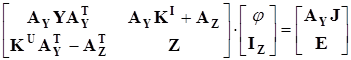 . (3.25) . (3.25)
Поставив I
1
и I
3
в первое уравнение, получим расширенное узловое уравнение:
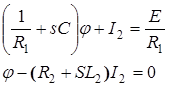
или в матричной форме:
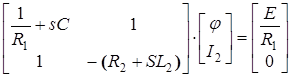 . .
Учитывая, что ветви 1, 2, 3, 4 – Y-ветви, а 5, 6 – Z-ветви, запишем матрицу соединений, разделив ее на Ay
- и Az
-подматрицы:
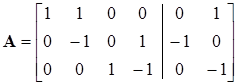 = [Ay
,
Az
]. = [Ay
,
Az
].
Приведем матрицы проводимостей ветвей Y, сопротивлений Z и коэффициентов передачи КI
и КU
:
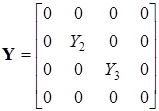 , , 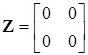 , , 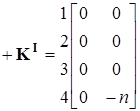 , , 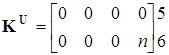 . .
Найдем необходимые произведения матриц:
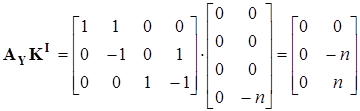
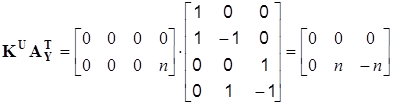 . .
Теперь расширенные узловые уравнения: имеют вид:
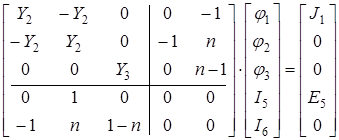 . .
3.9 Вычисления с комплексными числами в
MathCAD
В MathCAD определена мнимая единица j
:  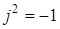 , , 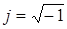 и, следовательно, определены комплексные числа и операции с ними. Для того, чтобы ввести в MathCAD мнимую единицу, следует набрать на клавиатуре <1
><j
> (в рабочем документе будет отображен символ i
, который MathCAD при таком способе ввода воспринимает как мнимую единицу). и, следовательно, определены комплексные числа и операции с ними. Для того, чтобы ввести в MathCAD мнимую единицу, следует набрать на клавиатуре <1
><j
> (в рабочем документе будет отображен символ i
, который MathCAD при таком способе ввода воспринимает как мнимую единицу).
Комплексные числа записывают в MathCAD в общепринятой математической нотации. Это означает, что выражение z
=
a
+
bj
, где а
и b
– действительные числа, воспринимается как комплексное число, действительная часть которого равна а
, а мнимая – b
.
В MathCAD можно определять комплексные числа в алгебраической, тригонометрической и показательной форме; однако при символьных вычислениях (с помощью знака символьных преобразований ® или ключевого слова complex) комплексное число все равно отображается в алгебраической форме.
Для вычислений с комплексными числами в MathCAD определены все арифметические операции, а также специфические для комплексной арифметики операции:
- Re(z
) – действительная часть комплексного числа z
;
- Im(z
) – мнимая часть комплексного числа z
;
- аrg(z
) – главное значение аргумента комплексного числа z
;
- 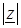 – модуль – модуль 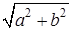 комплексного числа Z
; комплексного числа Z
;
- 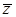 =
a
-
jb
– число, комплексно сопряженное к числу z
. =
a
-
jb
– число, комплексно сопряженное к числу z
.
В MathCAD можно вычислять значения элементарных функций, как действительного, так и комплексного аргумента. Однако при вычислении значений многозначных функций вычисляются только главные значения. Для того, чтобы вычислить все значения многозначных функций, пользователь должен определить их в рабочем документе соответствующими выражениями.
Если уравнение имеет комплексные корни, то MathCAD вычисляет не только действительные, но и комплексные корни.
3.10 Расчет электрических цепей с трансформаторами
Уравнения двухобмоточного трансформатора
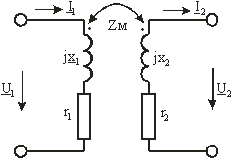
Рис. 3.14
могут быть представлены в виде уравнений четырехполюсника в Z-форме:
 (3.26) (3.26)
При выбранном направлении токов и напряжений
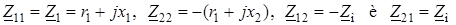 . .
Цепь с каскадным соединением трансформаторов
Если известно сопротивление вторичной цепи 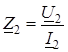 , можно из второго уравнения (3.26) выразить I
2
через I
1
и таким образом пересчитать сопротивление вторичной цепи в первичную: , можно из второго уравнения (3.26) выразить I
2
через I
1
и таким образом пересчитать сопротивление вторичной цепи в первичную:
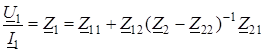 . (3.27) . (3.27)
Пересчет сопротивления Z
2
из вторичной цепи в первичную дает возможность при известном напряжении на входе трансформатора определить ток первичной цепи. Для определения тока и напряжения вторичной цепи можно воспользоваться уравнением четырехполюсника в В-форме:
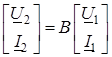 , (3.28) , (3.28)
Литература
1. Теоретические основы электротехники: В 3 т. Учебник для вузов. Том 1, 2. – 4-е изд. / К.С. Демирчян, Л.Р. Нейман, Н.В. Коровкин, В.Л. Чечурин. – СПБ Питер, 2004. – 463, 576 с.
2. Основы теории цепей: Учебник для вузов. Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. – 5-е изд., перераб. – М.: Энергоатомиздат, 1989. – 528 с.
3. К.С. Демирчян, П.А. Бутырин. «Моделирование и машинный расчет электрических цепей». – М.: ВШ., 1988. – 335 с.
4. И. Влах, К. Сингхал. Машинные методы анализа и проектирование электронных схем. – М.: Радиосвязь, 1988. – 560 с.
5. Данилов Л.В. и др. Теория нелинейных электрических цепей (Л.В. Данилов, П.Н. Матханов, Е.С. Филиппов). – Л.: Энергоатомиздат, Ленинград. отд-ие, 1999. – 256 с.
6. Леон О. Чуа и Пен-Мин Лиин. Машинный анализ электронных схем (алгоритмы и вычислительные методы). – М.: Энергия, 1980. – 640 с.
7. Плис А.И., Сливина Н.А. MathCAD. Математический практикум для инженеров и экономистов: учеб. Пособие – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2003. – 656 с.
8. Шабалин В.Д. Машинное моделирование электрических цепей. – Кострома: Изд. Костромской ГСХА, 200. – 80 с.
9. Шабалин В.Д. Пересчет сопротивления нагрузки трехфазной цепи, содержащей трансформатор. / Актуальные проблемы науки в агропромышленном комплексе: материалы 58-й международной научно-практической конференции: в 3 т. Т. 3. – Кострома: КГСХА, 2007. с. 184–185.
|