РЕФЕРАТ
Пояснительная записка содержит: 43 страницы, 8 рисунков, 5 формул.
Цель – закрепление знаний, полученных при изучении технологии программирования гибких компьютеризированных систем; приобретение практических навыков в создании программных проектов с использованием среды программирования MSVisualStudio; изучение принципов и методов создания приложений с использованием библиотеки MicrosoftFoundationalClasses (MFC), изучение основ теории нечетких множеств, в частности функций принадлежности.
Результат – исполняемое приложение, реализующее построение функций принадлежности и определение степени принадлежности выбранной точки.
Ключевые слова: НЕЧЕТКОЕ МНОЖЕСТВО, ФУНКЦИЯ ПРИНАДЛЕЖНОСТИ, СТЕПЕНЬ ПРИНАДЛЕЖНОСТИ, ПРОГРАММА, C++, MFC, MICROSOFTVISUALSTUDIO.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. АНАЛИЗ ТЕХНИЧЕСКОГО ЗАДАНИЯ
2. АНАЛИЗ ТЕХНИЧЕСКИХ РЕШЕНИЙ
2.1 Библиотека MFC
2.2 Нечеткая логика – математические основы
2.3 Применение нечеткой логики
3.ПРОЕКТИРОВАНИЕ ФУНКЦИОНАЛЬНОЙ СТРУКТУРЫ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
4.ПРОГРАММНАЯ РЕАЛИЗАЦИЯ
ВЫВОДЫ
ПЕРЕЧЕНЬ ССЫЛОК
Приложение А. Исходный текст программы
ВВЕДЕНИЕ
Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств и классической формальной логики. Данные понятия были впервые предложены американским ученым Лотфи Заде (Lotfi Zadeh) в статье "Fuzzy Sets" (Нечеткие Множества) в 1965 году в журнале Information and Control. Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.
Идея, лежащая в основе теории нечетких множеств, заключается в том, что человек в своей повседневной жизни мыслит и принимает решения на основе нечетких понятий. Создание теории нечетких множеств ‑ это попытка формализовать человеческий способ рассуждений. Развитие вычислительной техники позволяет в настоящее время создавать на базе теории нечетких множеств системы нечеткой логики, которые копируют способ рассуждений человека.[2]
Прежде чем нечеткий подход к моделированию сложных систем получил признание во всем мире, прошло не одно десятилетие с момента зарождения теории нечетких множеств. И на этом пути развития нечетких систем принято выделять три периода[5].
Реклама

Первый период (конец 60-х – начало 70 гг.) характеризуется развитием теоретического аппарата нечетких множеств (Л. Заде, Э. Мамдани, Беллман). Во втором периоде (70–80-е годы) появляются первые практические результаты в области нечеткого управления сложными техническими системами (парогенератор с нечетким управлением). Одновременно стало уделяться внимание вопросам построения экспертных систем, построенных на нечеткой логике, разработке нечетких контроллеров. Нечеткие экспертные системы для поддержки принятия решений находят широкое применение в медицине и экономике. Наконец, в третьем периоде, который длится с конца 80-х годов и продолжается в настоящее время, появляются пакеты программ для построения нечетких экспертных систем, а области применения нечеткой логики заметно расширяются. Она применяется в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятия управленческих решений и многих других.
Триумфальное шествие нечеткой логики по миру началось после доказательства в конце 80-х Бартоломеем Коско знаменитой теоремы FAT (Fuzzy Approximation Theorem). В бизнесе и финансах нечеткая логика получила признание после того как в 1988 году экспертная система на основе нечетких правил для прогнозирования финансовых индикаторов единственная предсказала биржевой крах. И количество успешных фаззи-применений в настоящее время исчисляется тысячами.
В гибких компьютеризированных системах, как правило, обрабатываемые данные носят четкий, числовой характер. Однако иногда могут присутствовать неточности и неопределенности, часто приходится находить разумный компромисс между понятиями "точность" и "важность". В этом случае на помощь приходит концепция нечеткой логики.
1.АНАЛИЗ ТЕХНИЧЕСКОГО ЗАДАНИЯ
Целью работы является разработка исполняемого Win32 приложения с визуальным интерфейсом, обеспечивающим построение функций принадлежности. Для реализации отмеченной функциональности необходимо:
а) спроектировать визуальный интерфейс приложения, включающий в себя кнопки доступа к функциям построения графика, выбора типа функции принадлежности, полей ввода исходных данных;
б) определить область отображения графика;
в) реализовать построение функций принадлежности таких типов: треугольная, трапециидальная, гауссовская, расширенная гауссовская, сигмоидальная с учетом масштаба;
Реклама

г) реализовать возможность определения степени принадлежности точки для заданного типа функции принадлежности;
д) произвести тестирование приложения на множестве исходных данных.
В целях сокращения времени на разработку визуального интерфейса в операционной системе MicrosoftWindows, целесообразно использовать функциональные возможности динамически исполняемой библиотеки MFC в среде разработки MicrosoftVisualStudio 6. Библиотека имеет собственную иерархическую организацию программных компонент, позволяющих создавать различные визуальные элементы управления.
Таким образом, выполнение технического задания требует программной реализации приложения с визуальным интерфейсом для построения функций принадлежности по исходным данным.
2. АНАЛИЗ ТЕХНИЧЕСКИХ РЕШЕНИЙ
2.1 Библиотека MFC
Система MicrosoftWindows была разработана до того времени, когда идея объектно-ориентированного программирования нашла свое отражение в языке C++. Приложения на языке С реализовывались с применением функций программного интерфейса, называемых иногда функциями API (ApplicationProgrammingInterface). Однако идеи объектно-ориентированного программирования требуют и наличия средств, позволяющих, с одной стороны, программировать в терминах классов, а с другой – сохранить возможность использования в приложениях функций API. Именно такой объектно-ориентированный интерфейс для Windows обеспечивает библиотека классов MFC (Microsoft Foundation Classes), входящая в состав пакета Visual C++.
Эта библиотека классов позволяет:
а) значительно сократить усилия по написанию программного кода приложений Windows;
б) уменьшить размер программного кода;
в) обрабатывать сообщения непосредственно методами класса без программирования цикла обработки сообщений;
г) выполнять непосредственный вызов любой функции Windows С;
д) легко преобразовывать Си-приложения в приложения на языке C++;
е) использовать все функции Windows API;
ж) легче адаптировать приложения к различным платформам, использовать как статически, так и динамически подключаемые библиотеки MFC;
з) значительно упростить применение таких возможностей, как элементы управления OLE, работа с базами данных, средства печати, управление наборами инструментария;
и) более эффективно использовать объектную ориентированность языка C++.

Рисунок 2.1 – Иерархия классов в библиотеке MFC
Следует отметить, что MFC инкапсулирует функции API в форме C++. Эта библиотека классов позволяет работать в терминах различных элементов Windows, таких, как окна, диалоги, элементы управления, а также в терминах графического интерфейса: контекст устройства, кисть и перо. Библиотека MFC создана как иерархический набор классов, позволяющих реализовывать Windows-приложения различных типов: диалоги, приложения с SDI или MDI интерфейсом, приложения, поддерживающие работу с базами данных, OLE-приложения. Базовым классом большинства классов библиотеки является класс CObject. В этом классе инкапсулированы общие методы работы с объектами: использование дампа объектов класса при отладке приложения, доступ к информации о классе объекта времени выполнения, сохранение и восстановление объектов класса. Большую часть библиотеки составляют классы, наследуемые от CObject и реализующие архитектуру приложения (рисунок 2.1)[1]: CWinThread, CWinApp, CDoc-Template, CDocument, CFrameWnd, CView и др.
2.2 Нечеткая логика ‑ математические основы
Нечеткое множество ‑ это пара (A, m), где A ‑ имя нечеткого множества, например: БОЛЬШОЙ, МОЛОДОЙ, ОТРИЦАТЕЛЬНО МАЛЫЙ, а m ‑ функция m:X-->L, называемая функцией принадлежности и обозначаемая обычно греческой буквой m. Часто полагается L = [0,1], а в качестве X используется некоторое множество вещественных чисел. m(x) интерпретируется как степень принадлежности элемента x из X нечеткому множеству A.
Характеристикой нечеткого множества выступает функция принадлежности (Membership Function)[4]. Обозначим через MFc
(x) – степень принадлежности к нечеткому множеству C, представляющей собой обобщение понятия характеристической функции обычного множества. Тогда нечетким множеством С называется множество упорядоченных пар вида C={MFc
(x)/x}, MFc
(x) [0,1]. Значение MFc
(x)=0 означает отсутствие принадлежности к множеству, 1 – полную принадлежность.
Проиллюстрируем это на простом примере. Формализуем неточное определение 'горячий чай'. В качестве x (область рассуждений) будет выступать шкала температуры в градусах Цельсия. Очевидно, что она будет изменяется от 0 до 100 градусов. Нечеткое множество для понятия 'горячий чай' может выглядеть следующим образом:
C={0/0; 0/10; 0/20; 0,15/30; 0,30/40; 0,60/50; 0,80/60; 0,90/70; 1/80; 1/90; 1/100}.
Так, чай с температурой 60 С принадлежит к множеству 'Горячий' со степенью принадлежности 0,80. Для одного человека чай при температуре 60 С может оказаться горячим, для другого – не слишком горячим. Именно в этом и проявляется нечеткость задания соответствующего множества.
Для нечетких множеств, как и для обычных, определены основные логические операции[5]. Самыми основными, необходимыми для расчетов, являются пересечение и объединение.
Пересечение двух нечетких множеств (нечеткое "И"): AÈB: MFAB(x)=min(MFA(x), MFB(x)).
Объединение двух нечетких множеств (нечеткое "ИЛИ"): AÇB: MFAB(x)=max(MFA(x), MFB(x)).
В теории нечетких множеств разработан общий подход к выполнению операторов пересечения, объединения и дополнения, реализованный в так называемых треугольных нормах и конормах. Приведенные выше реализации операций пересечения и объединения – наиболее распространенные случаи t-нормы и t-конормы.
Для описания нечетких множеств вводятся понятия нечеткой и лингвистической переменных.[4]
Нечеткая переменная описывается набором (N,X,A), где N – это название переменной, X – универсальное множество (область рассуждений), A – нечеткое множество на X.
Значениями лингвистической переменной могут быть нечеткие переменные, т.е. лингвистическая переменная находится на более высоком уровне, чем нечеткая переменная. Каждая лингвистическая переменная состоит из:
- названия;
- множества своих значений, которое также называется базовым терм-множеством T. Элементы базового терм-множества представляют собой названия нечетких переменных;
- универсального множества X;
- синтаксического правила G, по которому генерируются новые термы с применением слов естественного или формального языка;
- семантического правила P, которое каждому значению лингвистической переменной ставит в соответствие нечеткое подмножество множества X.
Рассмотрим такое нечеткое понятие как 'Цена акции'. Это и есть название лингвистической переменной. Сформируем для нее базовое терм-множество, которое будет состоять из трех нечетких переменных: 'Низкая', 'Умеренная', 'Высокая' и зададим область рассуждений в виде X=[100;200] (единиц). Последнее, что осталось сделать – построить функции принадлежности для каждого лингвистического терма из базового терм-множества T.
Существует свыше десятка типовых форм кривых для задания функций принадлежности.[2] Наибольшее распространение получили: треугольная, трапецеидальная и гауссовская функции принадлежности.
Треугольная функция (рисунок 2.2) принадлежности определяется тройкой чисел (a,b,c), и ее значение в точке x вычисляется согласно выражению:
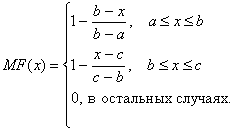 (2.1) (2.1)
При (b-a)=(c-b) имеем случай симметричной треугольной функции принадлежности, которая может быть однозначно задана двумя параметрами из тройки (a,b,c).
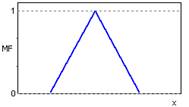
Рисунок 2.2 – Треугольная функция принадлежности
Аналогично для задания трапецеидальной функции (рисунок 2.3) принадлежности необходима четверка чисел (a,b,c,d):
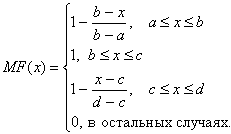 (2.2) (2.2)
При (b-a)=(d-c) трапецеидальная функция принадлежности принимает симметричный вид.
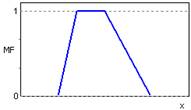
Рисунок 2.3 – Трапециидальная функция принадлежности
Функция принадлежности гауссова типа(рисунок 2.4) описывается формулой
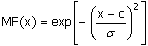 (2.3) (2.3)
и оперирует двумя параметрами. Параметр c обозначает центр нечеткого множества, а параметр s отвечает за крутизну функции.
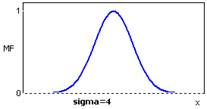
Рисунок 2.4 – Гауссовская функция принадлежности
Расширенная функция принадлежности гауссова типа(рисунок 2.5) описывается формулой
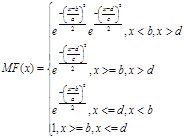 (2.4) (2.4)
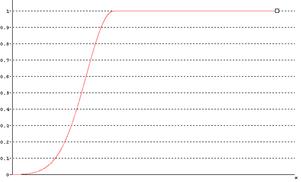
Рисунок 2.5 – Расширенная гауссовская функция принадлежности
Сигмоидальная функция принадлежности (рисунок 2.6) описывается формулой
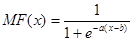 (2.5) (2.5)
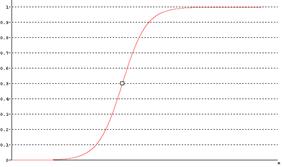
Рисунок 2.6 – Сигмоидальная функция принадлежности
2.3 Применение нечеткой логики
Гибридизация методов интеллектуальной обработки информации – девиз, под которым прошли 90-е годы у западных и американских исследователей. В результате объединения нескольких технологий искусственного интеллекта появился специальный термин – 'мягкие вычисления' (soft computing), который ввел Л. Заде в 1994 году. В настоящее время мягкие вычисления объединяют такие области как[5]: нечеткая логика, искусственные нейронные сети, вероятностные рассуждения и эволюционные алгоритмы. Они дополняют друг друга и используются в различных комбинациях для создания гибридных интеллектуальных систем.
Влияние нечеткой логики оказалось, пожалуй, самым обширным. Подобно тому, как нечеткие множества расширили рамки классической математическую теорию множеств, нечеткая логика 'вторглась' практически в большинство методов Data Mining, наделив их новой функциональностью. Ниже приводятся наиболее интересные примеры таких объединений.
Нечеткие нейронные сети. Нечеткие нейронные сети (fuzzy-neural networks) осуществляют выводы на основе аппарата нечеткой логики, однако параметры функций принадлежности настраиваются с использованием алгоритмов обучения НС. Поэтому для подбора параметров таких сетей применим метод обратного распространения ошибки, изначально предложенный для обучения многослойного персептрона. Для этого модуль нечеткого управления представляется в форме многослойной сети. Нечеткая нейронная сеть как правило состоит из четырех слоев: слоя фазификации входных переменных, слоя агрегирования значений активации условия, слоя агрегирования нечетких правил и выходного слоя.
Наибольшее распространение в настоящее время получили архитектуры нечеткой НС вида ANFIS и TSK. Доказано, что такие сети являются универсальными аппроксиматорами.
Быстрые алгоритмы обучения и интерпретируемость накопленных знаний – эти факторы сделали сегодня нечеткие нейронные сети одним из самых перспективных и эффективных инструментов мягких вычислений.
Адаптивные нечеткие системы. Классические нечеткие системы обладают тем недостатком, что для формулирования правил и функций принадлежности необходимо привлекать экспертов той или иной предметной области, что не всегда удается обеспечить. Адаптивные нечеткие системы (adaptive fuzzy systems) решают эту проблему. В таких системах подбор параметров нечеткой системы производится в процессе обучения на экспериментальных данных. Алгоритмы обучения адаптивных нечетких систем относительно трудоемки и сложны по сравнению с алгоритмами обучения нейронных сетей, и, как правило, состоят из двух стадий:
- генерация лингвистических правил;
- корректировка функций принадлежности. Первая задача относится к задаче переборного типа, вторая – к оптимизации в непрерывных пространствах. При этом возникает определенное противоречие: для генерации нечетких правил необходимы функции принадлежности, а для проведения нечеткого вывода – правила. Кроме того, при автоматической генерации нечетких правил необходимо обеспечить их полноту и непротиворечивость.
Значительная часть методов обучения нечетких систем использует генетические алгоритмы. В англоязычной литературе этому соответствует специальный термин – Genetic Fuzzy Systems.
Значительный вклад в развитие теории и практики нечетких систем с эволюционной адаптацией внесла группа испанских исследователей во главе с Ф. Херрера (F. Herrera).
Нечеткие запросы. Нечеткие запросы к базам данных (fuzzy queries) – перспективное направление в современных системах обработки информации. Данный инструмент дает возможность формулировать запросы на естественном языке, например: 'Вывести список недорогих предложений о съеме жилья близко к центру города', что невозможно при использовании стандартного механизма запросов. Для этой цели разработана нечеткая реляционная алгебра и специальные расширения языков SQL для нечетких запросов. Большая часть исследований в этой области принадлежит западноевропейским ученым Д. Дюбуа и Г. Праде.
Нечеткие ассоциативные правила. Нечеткие ассоциативные правила (fuzzy associative rules) – инструмент для извлечения из баз данных закономерностей, которые формулируются в виде лингвистических высказываний. Здесь введены специальные понятия нечеткой транзакции, поддержки и достоверности нечеткого ассоциативного правила.
Нечеткие когнитивные карты. Нечеткие когнитивные карты (fuzzy cognitive maps) были предложены Б. Коско в 1986 г. и используются для моделирования причинных взаимосвязей, выявленных между концептами некоторой области. В отличие от простых когнитивных карт, нечеткие когнитивные карты представляют собой нечеткий ориентированный граф, узлы которого являются нечеткими множествами. Направленные ребра графа не только отражают причинно-следственные связи между концептами, но и определяют степень влияния (вес) связываемых концептов. Активное использование нечетких когнитивных карт в качестве средства моделирования систем обусловлено возможностью наглядного представления анализируемой системы и легкостью интерпретации причинно-следственных связей между концептами. Основные проблемы связаны с процессом построения когнитивной карты, который не поддается формализации. Кроме того, необходимо доказать, что построенная когнитивная карта адекватна реальной моделируемой системе. Для решения данных проблем разработаны алгоритмы автоматического построения когнитивных карт на основе выборки данных.
Нечеткая кластеризация. Нечеткие методы кластеризации, в отличие от четких методов (например, нейронные сети Кохонена), позволяют одному и тому же объекту принадлежать одновременно нескольким кластерам, но с различной степенью. Нечеткая кластеризация во многих ситуациях более 'естественна', чем четкая, например, для объектов, расположенных на границе кластеров. Наиболее распространены: алгоритм нечеткой самоорганизации c-means и его обобщение в виде алгоритма Густафсона-Кесселя.
Список можно продолжить и дальше: нечеткие деревья решений, нечеткие сети Петри, нечеткая ассоциативная память, нечеткие самоорганизующиеся карты и другие гибридные методы.
3. ПРОЕКТИРОВАНИЕ ФУНКЦИОНАЛЬНОЙ СТРУКТУРЫ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
Проектирование приложений с использованием библиотеки MFC основывается на предопределенной структуре иерархии взаимодействия стандартных классов (рисунок 2.1). Для реализации необходимой функциональности приложения достаточным является использование обычного диалогового окна. При этом основная структура приложения будет определяться двумя классами:
- класс CFuzzyApp, обеспечивающий функциональность динамического исполнения приложения в целом, порожденный от базового MFC-классаCWinApp;
- класс CFuzzyDlg, обеспечивающий работу с визуальными компонентами операционной среды MicrosoftWindows, порожденный от базового MFC-классаCDialog;
Класс CFuzzyApp наследуется от класса приложения CWinApp. Основной перегружаемым виртуальным методом данного класса является метод CFuzzyApp::InitInstance(). Перегрузка метода необходима для инициализации вспомогательных компонент приложения, а также для реализации связи визуального окна компонентов MSWindows с исполняемым приложением. В целом, метод CFuzzyApp::InitInstance() готовит приложение к работе.
Как известно [3], программы, работающие в среде MSWindows, имеют графический интерфейс пользователя (GUI – GraphicalUserInterface). Исходные данные поступают в программу через диалоговое окно. Например, пользователь может сообщить приложению о выборе функции, включив один из переключателей (класс CButton(BS_RADIOBUTTON, …)) или выполнив некоторое действие с другими элементами управления. Для каждого диалогового окна в приложении есть две вещи, которые необходимо разработать, – ресурсы окна и класс окна.
Ресурсы окна используются программой для того, чтобы вывести на экран его изображение и изображения элементов управления, которые входят в него. В класс окна включены его параметры и методы, ответственные за вывод окна на экран. Они работают совместно для достижения общей цели – обеспечить максимально эффективное взаимодействие пользователя и программы.
Ресурсы диалогового окна создаются посредством редактора ресурсов, с помощью которого возможно включать в состав окна необходимые элементы управления и размещать их в пространстве окна желаемым образом. Помощь в создании класс окна может оказать ClassWizard, встроенный в стандартом наборе MSVisualStudio. Как правило, класс конкретного диалогового окна в проекте является производным от базового класса CDialog, имеющегося в составе MFC. Обычно каждый элемент управления, включенный в состав ресурсов окна, имеет в классе окна соответствующий член класса. Для того чтобы вывести диалоговое окно на экран, необходимо вызвать метод его класса. Для того, чтобы установить значения по умолчанию для элементов управления перед выводом окна на экран или считать состояние элементов управления после завершения работы пользователя, необходимо обращаться к членам класса.
Таким образом, первым шагом проектирования MFC-приложения является формирование ресурса окна, который служит своего рода шаблоном для MSWindows. Когда MSWindows обнаруживает ресурс окна в программе, она использует команды из этого ресурса для конструирования работающего окна.
Далее в редакторе ресурсов в диалоговое окно должны быть добавлены необходимые элементы управления – кнопки, радиокнопки, поля ввода, текстовые метки, декоративные элементы (GroupBox) и элемент Picture.
Проектируемый интерфейс изображен на рисунке 3.1.

Рисунок 3.1 – Проектируемый интерфейс
Когда сформированы ресурсы окна и подготовлен класс CFuzzyDlg для окна приложения, можно создавать объект этого класса в самой программе и выводить на экран связанное с ним диалоговое окно. В рассматриваемом случае, достаточно в методе CFuzzyApp::InitInstance() вывести диалоговое окно на экран сразу после запуска приложения, используя базовый метод CDialog::DoModal() класса диалогового окна CDialog.
Отображение результатов построения функции производится в элемент Picture. Для вывода графики в Windows и в Visual C++ используется понятие контекста устройства (device context). Контекст устройства ‑ это объект класса CDC, содержащий все методы для построения изображения в окне.
Таким образом спроектированная структура программного обеспечения является адекватной решению поставленной в техническом задании задачи.
4. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ ПОСТАВЛЕННОЙ ЗАДАЧИ
Программная реализация разработанной выше структуры приложения состоит в разработке исполняемого Win32-приложения в среде визуального программирования MSVisualStudio. Проект программного обеспечения состоит из трех классов – CFuzzyApp, CFuzzyDlg, CFuzzy_.
В классе CFuzzy_ выполняются непосредственные расчеты значений функций неопределенности. Расчеты выполняются функциями-членами[6] этого класса:
- CFuzzy_::fisTriangleMf (double x, double *params) – вычисление значений треугольной функции принадлежности;
- CFuzzy_::fisTrapezoidMf(doublex, double *params) – вычисление значений трапециидальной функции принадлежности;
- CFuzzy_::fisGaussianMf(doublex, double *params) – вычисление значений гауссовской функции принадлежности;
- CFuzzy_::fisGaussian2Mf(doublex, double *params) – вычисление значений расширенной гауссовской функции принадлежности;
- CFuzzy_::fisSigmoidMf(doublex, double *params) – вычисление значений сигмоидальной функции принадлежности.
Например, функция CFuzzy_::fisTrapezoidMf(double x, double *params):
/* Trapezpoidal membership function */
double CFuzzy_::fisTrapezoidMf(double x, double *params)
{
double a = params[0], b = params[1], c = params[2], d = params[3];
double y1 = 0, y2 = 0;
if (a>b) {
fisError("Illegal parameters in fisTrapezoidMf() --> a > b");
}
if (b>c)
{
fisError("Illegal parameters in fisTrapezoidMf() --> b > c");
}
if (c>d) {
fisError("Illegal parameters in fisTrapezoidMf() --> c > d");
}
if (b <= x)
y1 = 1;
else if (x < a)
y1 = 0;
else if (a != b)
y1 = (x-a)/(b-a);
if (x <= c)
y2 = 1;
else if (d < x)
y2 = 0;
else if (c != d)
y2 = (d-x)/(d-c);
return(MIN(y1, y2));
}
Так же в классе CFuzzy_ находится функция-член fisError(char *msg), которая реализует выдачу сообщения об ошибке, если пользователь ввел неправильные данные. Само сообщение передается в функцию fisError(char *msg) в качестве параметра из функций, вычисляющих значение функций принадлежности.
В классе CFuzzyApp реализована базовая функциональность стандартного MFC-приложения. В частности, переопределен виртуальный метод базового класса CWinApp::InitInstance():
BOOL CFuzzyApp::InitInstance()
{
AfxEnableControlContainer();
#ifdef _AFXDLL
Enable3dControls();
#else
Enable3dControlsStatic();
#endif
CFuzzyDlg dlg;
m_pMainWnd = &dlg;
dlg.DoModal();
returnFALSE;
}
В результате исполняемый код приложения был связан со спроектированным ранее визуальным интерфейсом (рисунок 3.1). В качестве члена в классе CFuzzyApp была введена переменная[6] dlg типа CFuzzyDlg. Она обеспечивает непосредственную связь приложения с интерфейсом, предоставляемого пользователю.
В классе CFuzzyDlg выполняется инициализация диалога и элементов управления.
BOOL CFuzzyDlg::OnInitDialog()
{
CDialog::OnInitDialog();
SetIcon(m_hIcon, TRUE);
SetIcon(m_hIcon, FALSE);
par_a.SetWindowText("1");
par_b.SetWindowText("3");
par_c.SetWindowText("5");
par_d.SetWindowText("9");
R_Tri=(CButton*)GetDlgItem(IDC_RADIO1);
R_Tra=(CButton*)GetDlgItem(IDC_RADIO2);
R_Ga=(CButton*)GetDlgItem(IDC_RADIO3);
R_Ga2=(CButton*)GetDlgItem(IDC_RADIO4);
R_Sig=(CButton*)GetDlgItem(IDC_RADIO5);
param = new double[3];
WIDTH = 600;
HEIGHT = 400;
return TRUE;
}
С помощью элементов управления, являющимися объектами класса CEdit – par_a, par_b, par_c, par_d реализуется ввод параметров для функций принадлежности.
В классе CFuzzyDlgимеются функции для построения координатных осей (функция CFuzzyDlg::Axis()) и отображения графика функции принадлежности (одна из функций CFuzzyDlg::PlotTriangle(), CFuzzyDlg::PlotTrapezoid(), CFuzzyDlg::PlotGaussian(),CFuzzyDlg::PlotGaussian2(), CFuzzyDlg::PlotSigmoid() в зависимости от типа функции, выбранной пользователем). Вывод графика осуществляется с помощью класса CDC, который
При нажатии пользователем кнопки «Построить!!» происходит выполнение функции CFuzzyDlg::OnButton1(), из которой вызываются функции построения осей и функции принадлежности, выбранной пользователем или, если не был выбран тип функции, выдается сообщение «Выберите тип функции!!».
Функции для построения координатных осей (функция CFuzzyDlg::Axis()) и отображения графика функции принадлежности (одна из функций CFuzzyDlg::PlotTriangle(), CFuzzyDlg::PlotTrapezoid(), CFuzzyDlg::PlotGaussian(),CFuzzyDlg::PlotGaussian2(), CFuzzyDlg::PlotSigmoid() в зависимости от типа функции, выбранной пользователем) вызываются так же при перерисовке окна (обработка сообщения WM_PAINT с помощью функции CFuzzyDlg::OnPaint()).
void CFuzzyDlg::OnPaint()
{
CDialog::OnPaint();
Axis();
if (function==GAUSSIAN)
PlotGaussian();
else
if (function==TRIANGLE)
PlotTriangle();
else
if (function==TRAPEZOID)
PlotTrapezoid();
else
if (function==GAUSSIAN2)
PlotGaussian2();
else
if (function==SIGMOID)
PlotSigmoid();
}
Для того чтобы определить значение данной функции распределения в конкретной точке, в класс CFuzzyDlg была добавлена функция обработки сообщения перемещения манипулятора «Мышь» WM_MOUSEMOVE ‑ CFuzzyDlg::OnMouseMove(UINT nFlags, CPoint point). При перемещении мыши выводится значение точки x (с учетом масштаба) и степень принадлежности (значение данной функции принадлежности) этой точки x.
void CFuzzyDlg::OnMouseMove(UINT nFlags, CPoint point)
{
if (point.x>10 && point.x<WIDTH && point.y>10 && point.y<HEIGHT)
{
CDC *dc = m_grapho.GetDC();
CPen SolidPen;
SolidPen.CreatePen(PS_SOLID,1,RGB(255,255,255));
CBrush brush;
brush.CreateSolidBrush(RGB(255,255,255));
dc->SelectObject(brush);
dc->SelectObject(SolidPen);
dc->Rectangle(350,10,580,30);
double _tmp;
char crds[15];
CString coords;
_tmp=(point.x-36)*1000/kX+_par;
itoa((int)(_tmp),crds,10);
coords=crds;
itoa(ABS((int)(_tmp*100)%100),crds,10);
(ABS((int)(_tmp*100)%100)<10)?coords+=".0":coords+=".";
coords+=crds;
if (function==GAUSSIAN)
gcvt(fuzzy.fisGaussianMf(_tmp,param),2,crds);
else
if (function==TRIANGLE)
gcvt(fuzzy.fisTriangleMf(_tmp,param),2,crds);
else
if (function==TRAPEZOID)
gcvt(fuzzy.fisTrapezoidMf(_tmp,param),2,crds);
else
if (function==GAUSSIAN2)
gcvt(fuzzy.fisGaussian2Mf(_tmp,param),2,crds);
else
if (function==SIGMOID)
gcvt(fuzzy.fisSigmoidMf(_tmp,param),2,crds);
else
crds[0]='\0';
CFont *font = new CFont();
font->CreateFont(14, 10, 0, 0, FW_NORMAL, 0, 0, 0, ANSI_CHARSET, OUT_DEFAULT_PRECIS,
CLIP_DEFAULT_PRECIS,DEFAULT_QUALITY, DEFAULT_PITCH | FF_SWISS, "Courier");
dc->SelectObject(font);
dc->TextOut(50,10,"Точка x:"+coords+" Степеньпринадлежности:"+crds);
}
CDialog::OnMouseMove(nFlags, point);
}
Результат выполнения программы изображен на рисунке 4.1. В данном случае построена сигмоидальная функция принадлежности.
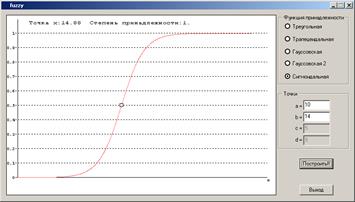
Рисунок 4.1 – Результат выполнения программы – сигмоидальная функция принадлежности
ВЫВОДЫ
Результатом работы является исполняемое Win32-приложение, позволяющее строить следующие функции принадлежности:
- треугольную;
- трапециидальную;
- гауссовскую;
- расширенную гауссовскую;
- сигмоидальную.
Так же программа позволяет определять значение степени принадлежности заданной точки x.
В ходе разработки приложения были изучены структура и возможности набора классов MFC, принципы проектирования визуального интерфейса пользователя в операционной среде MSWindows с использованием среды разработки MSVisualStudio. Было замечено, что классы MFC существенно ускоряют процесс создания приложений для операционной системы MicrosoftWindows.
Так же были изучены основы теории нечетких множеств, в частности функции принадлежности.
ПЕРЕЧЕНЬ ССЫЛОК
1. Microsoft Developer Network Library ‑ April 2003
2. Васильев В.И., Ильясов Б.Г. Интеллектуальные системы управления с использованием нечеткой логики: Учеб. пособие / Уфимск. гос. авиац. техн. ун-т. -Уфа, 1995. -80 c
3. Грегори К. Использование VisualC++ 6. Специальное издание.: Пер. с англ. – М.: СПб.; К.: Издательский дом «Вильямс», 2003. – 849 с.
4. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. – М.: Мир, 1976.
5. Нечеткая логика ‑ математические основы ‑ BaseGroupLabs
http://www.basegroup.ru/fuzzylogic/math_print.htm
6. Страуструп Бьярн Язык программирования C++ Второе издание. – К.: ДиаСофт, 1993. – 480 с.
ПРИЛОЖЕНИЕ
ПриложениеА
Листингпрограммы
// Fuzzy_.h: interface for the CFuzzy_ class.
class CFuzzy_
{
public:
void fisError(char *msg);
CFuzzy_();
virtual ~CFuzzy_();
double CFuzzy_::fisTriangleMf(double x, double *params);
double fisTrapezoidMf(double x, double *params);
double fisGaussianMf(double x, double *params);
double fisGaussian2Mf(double x, double *params);
double fisSigmoidMf(double x, double *params);
};
// Fuzzy_.cpp: implementation of the CFuzzy_ class.
#include "stdafx.h"
#include "fuzzy.h"
#include "Fuzzy_.h"
#include <math.h>
#ifndef ABS
# define ABS(x) ( (x) > (0) ? (x): (-(x)) )
#endif
#ifndef MAX
# define MAX(x,y) ( (x) > (y) ? (x) : (y) )
#endif
#ifndef MIN
# define MIN(x,y) ( (x) < (y) ? (x) : (y) )
#endif
CFuzzy_::CFuzzy_()
{
}
CFuzzy_::~CFuzzy_()
{
}
/* Triangular membership function */
double CFuzzy_::fisTriangleMf(double x, double *params)
{
double a = params[0], b = params[1], c = params[2];
if (a>b)
{fisError("Illegal parameters in fisTriangleMf() --> a > b");return -1;}
if (b>c)
{fisError("Illegal parameters in fisTriangleMf() --> b > c");return -1;}
if (a == b && b == c)
return(x == a);
if (a == b)
return((c-x)/(c-b)*(b<=x)*(x<=c));
if (b == c)
return((x-a)/(b-a)*(a<=x)*(x<=b));
return(MAX(MIN((x-a)/(b-a), (c-x)/(c-b)), 0));
}
/* Trapezpoidal membership function */
double CFuzzy_::fisTrapezoidMf(double x, double *params)
{
double a = params[0], b = params[1], c = params[2], d = params[3];
double y1 = 0, y2 = 0;
if (a>b) {
fisError("Illegal parameters in fisTrapezoidMf() --> a > b");
}
if (b>c)
{
fisError("Illegal parameters in fisTrapezoidMf() --> b > c");
}
if (c>d) {
fisError("Illegal parameters in fisTrapezoidMf() --> c > d");
}
if (b <= x)
y1 = 1;
else if (x < a)
y1 = 0;
else if (a != b)
y1 = (x-a)/(b-a);
if (x <= c)
y2 = 1;
else if (d < x)
y2 = 0;
else if (c != d)
y2 = (d-x)/(d-c);
return(MIN(y1, y2));
}
/* Gaussian membership function */
double CFuzzy_::fisGaussianMf(double x, double *params)
{
double sigma = params[0], c = params[1];
double tmp;
if (sigma==0)
fisError("Illegal parameters in fisGaussianMF() --> sigma = 0");
tmp = (x-c)/sigma;
return(exp(-tmp*tmp/2));
}
/* Extended Gaussian membership function */
double CFuzzy_::fisGaussian2Mf(double x, double *params)
{
double sigma1 = params[0], c1 = params[1];
double sigma2 = params[2], c2 = params[3];
double tmp1, tmp2;
if ((sigma1 == 0) || (sigma2 == 0))
fisError("Illegal parameters in fisGaussian2MF() --> sigma1 or sigma2 is zero");
tmp1 = x >= c1? 1:exp(-pow((x-c1)/sigma1, 2.0)/2);
tmp2 = x <= c2? 1:exp(-pow((x-c2)/sigma2, 2.0)/2);
return(tmp1*tmp2);
}
/* Sigmoidal membership function */
double CFuzzy_::fisSigmoidMf(double x, double *params)
{
double a = params[0], c = params[1];
return(1/(1+exp(-a*(x-c))));
}
void CFuzzy_::fisError(char *msg)
{
MessageBox(NULL,msg,"Error",MB_OK|MB_ICONSTOP);
}
// fuzzy.h : main header file for the FUZZY application CFuzzyApp
#include "resource.h"
class CFuzzyApp : public CWinApp
{
public:
CFuzzyApp();
// Overrides
// ClassWizard generated virtual function overrides
//{{AFX_VIRTUAL(CFuzzyApp)
public:
virtual BOOL InitInstance();
//}}AFX_VIRTUAL
// Implementation
//{{AFX_MSG(CFuzzyApp)
// NOTE - the ClassWizard will add and remove member functions here.
// DO NOT EDIT what you see in these blocks of generated code !
//}}AFX_MSG
DECLARE_MESSAGE_MAP()
};
// fuzzy.cpp : Defines the class behaviors for the application. CFuzzyApp
#include "stdafx.h"
#include "fuzzy.h"
#include "fuzzyDlg.h"
BEGIN_MESSAGE_MAP(CFuzzyApp, CWinApp)
//{{AFX_MSG_MAP(CFuzzyApp)
// NOTE - the ClassWizard will add and remove mapping macros here.
// DO NOT EDIT what you see in these blocks of generated code!
//}}AFX_MSG
ON_COMMAND(ID_HELP, CWinApp::OnHelp)
END_MESSAGE_MAP()
CFuzzyApp::CFuzzyApp()
{
}
CFuzzyApp theApp;
// CFuzzyApp initialization
BOOL CFuzzyApp::InitInstance()
{
AfxEnableControlContainer();
#ifdef _AFXDLL
Enable3dControls();
#else
Enable3dControlsStatic();
#endif
CFuzzyDlg dlg;
m_pMainWnd = &dlg;
dlg.DoModal();
// Since the dialog has been closed, return FALSE so that we exit the
// application, rather than start the application's message pump.
return FALSE;
}
// fuzzyDlg.h : header file
// CFuzzyDlg dialog
class CFuzzyDlg : public CDialog
{
// Construction
public:
void PlotTrapezoid();
void PlotTriangle();
void PlotGaussian();
void PlotSigmoid();
void PlotGaussian2();
void Axis();
CButton *R_Tri, *R_Tra, *R_Ga, *R_Ga2, *R_Sig;
CFuzzyDlg(CWnd* pParent = NULL);// standard constructor
// Dialog Data
//{{AFX_DATA(CFuzzyDlg)
enum { IDD = IDD_FUZZY_DIALOG };
CEditpar_d;
CEditpar_c;
CEditpar_b;
CEditpar_a;
CStaticm_grapho;
//}}AFX_DATA
// ClassWizard generated virtual function overrides
//{{AFX_VIRTUAL(CFuzzyDlg)
protected:
virtual void DoDataExchange(CDataExchange* pDX);// DDX/DDV support
//}}AFX_VIRTUAL
// Implementation
protected:
HICON m_hIcon;
// Generated message map functions
//{{AFX_MSG(CFuzzyDlg)
virtual BOOL OnInitDialog();
afx_msg void OnPaint();
afx_msg HCURSOR OnQueryDragIcon();
afx_msg void OnButton1();
afx_msg void OnMouseMove(UINT nFlags, CPoint point);
afx_msg void OnRadio1();
afx_msg void OnRadio2();
afx_msg void OnRadio3();
afx_msg void OnRadio4();
afx_msg void OnRadio5();
//}}AFX_MSG
DECLARE_MESSAGE_MAP()
};
// fuzzyDlg.cpp : implementation file
//
#include "stdafx.h"
#include "fuzzy.h"
#include "fuzzyDlg.h"
#include "fuzzy_.h"
#ifndef ABS
# define ABS(x) ( (x) > (0) ? (x): (-(x)) )
#endif
#ifndef MAX
# define MAX(x,y) ( (x) > (y) ? (x) : (y) )
#endif
#ifndef MIN
# define MIN(x,y) ( (x) < (y) ? (x) : (y) )
#endif
CFuzzy_ fuzzy;
double *param, x, y=0, kX=1000, _par=0;
int WIDTH, HEIGHT;
byte function=0;
const byte TRIANGLE = 1;
const byte TRAPEZOID = 2;
const byte GAUSSIAN = 3;
const byte GAUSSIAN2 = 4;
const byte SIGMOID = 5;
/////////////////////////////////////////////////////////////////////////////
// CFuzzyDlg dialog
CFuzzyDlg::CFuzzyDlg(CWnd* pParent /*=NULL*/)
: CDialog(CFuzzyDlg::IDD, pParent)
{
//{{AFX_DATA_INIT(CFuzzyDlg)
//}}AFX_DATA_INIT
// Note that LoadIcon does not require a subsequent DestroyIcon in Win32
m_hIcon = AfxGetApp()->LoadIcon(IDR_MAINFRAME);
}
void CFuzzyDlg::DoDataExchange(CDataExchange* pDX)
{
CDialog::DoDataExchange(pDX);
//{{AFX_DATA_MAP(CFuzzyDlg)
DDX_Control(pDX, IDC_EDITD, par_d);
DDX_Control(pDX, IDC_EDITC, par_c);
DDX_Control(pDX, IDC_EDITB, par_b);
DDX_Control(pDX, IDC_EDITA, par_a);
DDX_Control(pDX, IDC_GRAPHO, m_grapho);
//}}AFX_DATA_MAP
}
BEGIN_MESSAGE_MAP(CFuzzyDlg, CDialog)
//{{AFX_MSG_MAP(CFuzzyDlg)
ON_WM_PAINT()
ON_WM_QUERYDRAGICON()
ON_BN_CLICKED(IDC_BUTTON1, OnButton1)
ON_WM_MOUSEMOVE()
ON_BN_CLICKED(IDC_RADIO1, OnRadio1)
ON_BN_CLICKED(IDC_RADIO2, OnRadio2)
ON_BN_CLICKED(IDC_RADIO3, OnRadio3)
ON_BN_CLICKED(IDC_RADIO4, OnRadio4)
ON_BN_CLICKED(IDC_RADIO5, OnRadio5)
//}}AFX_MSG_MAP
END_MESSAGE_MAP()
/////////////////////////////////////////////////////////////////////////////
// CFuzzyDlg message handlers
BOOL CFuzzyDlg::OnInitDialog()
{
CDialog::OnInitDialog();
SetIcon(m_hIcon, TRUE);// Set big icon
SetIcon(m_hIcon, FALSE);
par_a.SetWindowText("1");
par_b.SetWindowText("3");
par_c.SetWindowText("5");
par_d.SetWindowText("9");
R_Tri=(CButton*)GetDlgItem(IDC_RADIO1);
R_Tra=(CButton*)GetDlgItem(IDC_RADIO2);
R_Ga=(CButton*)GetDlgItem(IDC_RADIO3);
R_Ga2=(CButton*)GetDlgItem(IDC_RADIO4);
R_Sig=(CButton*)GetDlgItem(IDC_RADIO5);
param = new double[3];
WIDTH = 600;
HEIGHT = 400;
// Set small icon
return TRUE; // return TRUE unless you set the focus to a control
}
// If you add a minimize button to your dialog, you will need the code below
// to draw the icon. For MFC applications using the document/view model,
// this is automatically done for you by the framework.
void CFuzzyDlg::OnPaint()
{
CDialog::OnPaint();
Axis();
if (function==GAUSSIAN)
PlotGaussian();
else
if (function==TRIANGLE)
PlotTriangle();
else
if (function==TRAPEZOID)
PlotTrapezoid();
else
if (function==GAUSSIAN2)
PlotGaussian2();
else
if (function==SIGMOID)
PlotSigmoid();
}
// The system calls this to obtain the cursor to display while the user drags
// the minimized window.
HCURSOR CFuzzyDlg::OnQueryDragIcon()
{
return (HCURSOR) m_hIcon;
}
void CFuzzyDlg::OnButton1()
{
Axis();
if (R_Tri->GetState()==1)
{
PlotTriangle();
} else
if (R_Tra->GetState()==1)
{
PlotTrapezoid();
} else
if (R_Ga->GetState()==1)
{
PlotGaussian();
}
else
if (R_Ga2->GetState()==1)
{
PlotGaussian2();
} else
if (R_Sig->GetState()==1)
{
PlotSigmoid();
}
else AfxMessageBox("Выберите тип функции!!", MB_ICONWARNING|MB_OK, 0);
}
void CFuzzyDlg::OnMouseMove(UINT nFlags, CPoint point)
{
if (point.x>10 && point.x<WIDTH && point.y>10 && point.y<HEIGHT)
{
CDC *dc = m_grapho.GetDC();
CPen SolidPen;
SolidPen.CreatePen(PS_SOLID,1,RGB(255,255,255));
CBrush brush;
brush.CreateSolidBrush(RGB(255,255,255));
dc->SelectObject(brush);
dc->SelectObject(SolidPen);
dc->Rectangle(350,10,580,30);
double _tmp;
char crds[15];
CString coords;
_tmp=(point.x-36)*1000/kX+_par;
itoa((int)(_tmp),crds,10);
coords=crds;
itoa(ABS((int)(_tmp*100)%100),crds,10);
(ABS((int)(_tmp*100)%100)<10)?coords+=".0":coords+=".";
coords+=crds;
if (function==GAUSSIAN)
gcvt(fuzzy.fisGaussianMf(_tmp,param),2,crds);
else
if (function==TRIANGLE)
gcvt(fuzzy.fisTriangleMf(_tmp,param),2,crds);
else
if (function==TRAPEZOID)
gcvt(fuzzy.fisTrapezoidMf(_tmp,param),2,crds);
else
if (function==GAUSSIAN2)
gcvt(fuzzy.fisGaussian2Mf(_tmp,param),2,crds);
else
if (function==SIGMOID)
gcvt(fuzzy.fisSigmoidMf(_tmp,param),2,crds);
else
crds[0]='\0';
CFont *font = new CFont();
font->CreateFont(14, 10, 0, 0, FW_NORMAL, 0, 0, 0, ANSI_CHARSET, OUT_DEFAULT_PRECIS,
CLIP_DEFAULT_PRECIS,DEFAULT_QUALITY, DEFAULT_PITCH | FF_SWISS, "Courier");
dc->SelectObject(font);
dc->TextOut(50,10,"Точка x:"+coords+" Степень принадлежности:"+crds);
}
CDialog::OnMouseMove(nFlags, point);
}
void CFuzzyDlg::OnRadio1()
{
par_d.EnableWindow(false);
}
void CFuzzyDlg::OnRadio2()
{
par_c.EnableWindow(true);
par_d.EnableWindow(true);
}
void CFuzzyDlg::OnRadio3()
{
par_c.EnableWindow(false);
par_d.EnableWindow(false);
}
void CFuzzyDlg::OnRadio4()
{
par_c.EnableWindow(true);
par_d.EnableWindow(true);
}
void CFuzzyDlg::OnRadio5()
{
par_c.EnableWindow(false);
par_d.EnableWindow(false);
}
void CFuzzyDlg::Axis()
{
CDC *_dc = m_grapho.GetDC();
CPen DotPen;
DotPen.CreatePen(PS_DOT,1,RGB(0,0,0));
CPen SolidPen;
SolidPen.CreatePen(PS_SOLID,1,RGB(0,0,0));
CBrush brush;
brush.CreateSolidBrush(RGB(255,255,255));
_dc->SelectObject(brush);
_dc->Rectangle(0,0,WIDTH, HEIGHT);
_dc->SelectObject(SolidPen);
_dc->MoveTo(25,10);
_dc->LineTo(25, HEIGHT-40);
_dc->MoveTo(20,HEIGHT-40);
_dc->LineTo(WIDTH-20, HEIGHT-40);
_dc->SelectObject(DotPen);;
CFont *font = new CFont();
font->CreateFont(12, 7, 0, 0, FW_NORMAL, 0, 0, 0, ANSI_CHARSET, OUT_DEFAULT_PRECIS,
CLIP_DEFAULT_PRECIS,DEFAULT_QUALITY, DEFAULT_PITCH | FF_SWISS, "Courier");
_dc->SelectObject(font);
_dc->TextOut(1,360-5,CString(" 0"));
for (int q=1;q<=10;q++)
{
_dc->MoveTo(20,360-q*32);
_dc->LineTo(580,360-q*32);
char iY[5];
gcvt(q*0.1,2,iY);
(q!=10)?_dc->TextOut(1,360-q*32-5,iY,3):_dc->TextOut(1,360-q*32-5,CString(" 1"));
}
_dc->TextOut(580,360,"x");
}
void CFuzzyDlg::PlotTriangle()
{
function=TRIANGLE;
CDC *dc = m_grapho.GetDC();
double tmp;
CString par_tmp;
par_a.GetWindowText(par_tmp);
param[0]=atof(par_tmp);
par_b.GetWindowText(par_tmp);
param[1]=atof(par_tmp);
par_c.GetWindowText(par_tmp);
param[2]=atof(par_tmp);
kX = 520000/ABS(param[2]-param[0]);
_par=param[0];
for (x=param[0];x<param[2];x+=ABS(param[2]-param[0])/8000)
{
tmp = fuzzy.fisTriangleMf(x,param);
tmp*=320;
dc->SetPixel((int)(((x)-param[0])*kX/1000+25),HEIGHT-40-(int)tmp, RGB(255,100,120));
}
dc->Rectangle((int)((param[0]-param[0])*kX/1000+25-4),HEIGHT-40-0*320-4,
(int)((param[0]-param[0])*kX/1000+25+4),HEIGHT-40-0*320+4);
dc->Rectangle((int)((param[1]-param[0])*kX/1000+25-4),HEIGHT-40-1*320-4,
(int)((param[1]-param[0])*kX/1000+25+4),HEIGHT-40-1*320+4);
dc->Rectangle((int)((param[2]-param[0])*kX/1000+25-4),HEIGHT-40-0*320-4,
(int)((param[2]-param[0])*kX/1000+25+4),HEIGHT-40-0*320+4);
}
void CFuzzyDlg::PlotTrapezoid()
{
function=TRAPEZOID;
CDC *dc = m_grapho.GetDC();
double tmp;
CString par_tmp;
par_a.GetWindowText(par_tmp);
param[0]=atof(par_tmp);
par_b.GetWindowText(par_tmp);
param[1]=atof(par_tmp);
par_c.GetWindowText(par_tmp);
param[2]=atof(par_tmp);
par_d.GetWindowText(par_tmp);
param[3]=atof(par_tmp);
kX = 520000/ABS(param[3]-param[0]);
_par=param[0];
for (x=param[0];x<param[3];x+=ABS(param[3]-param[0])/8000)
{
tmp = fuzzy.fisTrapezoidMf(x,param);
tmp*=320;
dc->SetPixel((int)(((x-param[0]))*kX/1000+25),HEIGHT-40-(int)tmp, RGB(255,100,100));
}
dc->Rectangle((int)((param[0]-param[0])*kX/1000+25-4),HEIGHT-40-0*320-4,
(int)((param[0]-param[0])*kX/1000+25+4),HEIGHT-40-0*320+4);
dc->Rectangle((int)((param[1]-param[0])*kX/1000+25-4),HEIGHT-40-1*320-4,
(int)((param[1]-param[0])*kX/1000+25+4),HEIGHT-40-1*320+4);
dc->Rectangle((int)((param[2]-param[0])*kX/1000+25-4),HEIGHT-40-1*320-4,
(int)((param[2]-param[0])*kX/1000+25+4),HEIGHT-40-1*320+4);
dc->Rectangle((int)((param[3]-param[0])*kX/1000+25-4),HEIGHT-40-0*320-4,
(int)((param[3]-param[0])*kX/1000+25+4),HEIGHT-40-0*320+4);
}
void CFuzzyDlg::PlotGaussian()
{
function=GAUSSIAN;
CDC *dc = m_grapho.GetDC();
double tmp;
CString par_tmp;
par_a.GetWindowText(par_tmp);
param[0]=atof(par_tmp);
par_b.GetWindowText(par_tmp);
param[1]=atof(par_tmp);
par_c.GetWindowText(par_tmp);
param[2]=atof(par_tmp);
par_d.GetWindowText(par_tmp);
param[3]=atof(par_tmp);
double _0=param[1];
do
{
tmp = fuzzy.fisGaussianMf(_0,param);
_0-=ABS(param[1])/1000;
}
while (tmp>=0.001);
kX = 520000/(2*ABS(param[1]-_0));
_par = _0;
for (x=_0;x<(param[1]+ABS(param[1]-_0));x+=ABS((param[1]+ABS(param[1]-_0))-_0)/8000)
{
tmp = fuzzy.fisGaussianMf(x,param);
tmp*=320;
dc->SetPixel((int)(((x)-_0)*kX/1000+25),HEIGHT-40-(int)tmp, RGB(255,100,100));
}
dc->Rectangle((int)((param[1]-_0)*kX/1000+25-4),HEIGHT-40-1*320-4,
(int)((param[1]-_0)*kX/1000+25+4),HEIGHT-40-1*320+4);
}
void CFuzzyDlg::PlotGaussian2()
{
function=GAUSSIAN2;
CDC *dc = m_grapho.GetDC();
double tmp;
CString par_tmp;
par_a.GetWindowText(par_tmp);
param[0]=atof(par_tmp);
par_b.GetWindowText(par_tmp);
param[1]=atof(par_tmp);
par_c.GetWindowText(par_tmp);
param[2]=atof(par_tmp);
par_d.GetWindowText(par_tmp);
param[3]=atof(par_tmp);
double _0=MIN(param[1], param[3]);
do
{
tmp = fuzzy.fisGaussian2Mf(_0,param);
_0-=ABS(MIN(param[1], param[3]))/10000;
}
while (tmp>=0.001);
kX = 520000/(ABS(MAX(param[1], param[3])-_0));
_par = _0;
for (x=_0;x<=MAX(param[1], param[3]);x+=ABS((MAX(param[1], param[3])-_0))/10000)
{
tmp = fuzzy.fisGaussian2Mf(x,param);
tmp*=320;
dc->SetPixel((int)(((x)-_0)*kX/1000+25),HEIGHT-40-(int)tmp, RGB(255,100,100));
}
dc->Rectangle((int)((MAX(param[1], param[3])-_0)*kX/1000+25-4),HEIGHT-40-1*320-4,
(int)((MAX(param[1], param[3])-_0)*kX/1000+25+4),HEIGHT-40-1*320+4);
}
void CFuzzyDlg::PlotSigmoid()
{
function=SIGMOID;
CDC *dc = m_grapho.GetDC();
double tmp;
CString par_tmp;
par_a.GetWindowText(par_tmp);
param[0]=atof(par_tmp);
par_b.GetWindowText(par_tmp);
param[1]=atof(par_tmp);
par_c.GetWindowText(par_tmp);
param[2]=atof(par_tmp);
par_d.GetWindowText(par_tmp);
param[3]=atof(par_tmp);
double _0=param[1],_1=param[1];
do
{
tmp = fuzzy.fisSigmoidMf(_0,param);
_0-=param[1]*0.0001;
}
while (tmp>=0.0001);
do
{
tmp = fuzzy.fisSigmoidMf(_1,param);
_1+=param[1]*0.0001;
}
while(tmp<0.99999);
kX = 520000/(ABS(_1-_0));
_par = _0;
for (x=_0;x<=_1;x+=ABS(param[1]*0.0001))
{
tmp = fuzzy.fisSigmoidMf(x,param);
tmp*=320;
dc->SetPixel((int)(((x)-_0)*kX/1000+25),HEIGHT-40-(int)tmp, RGB(255,100,100));
}
dc->Rectangle((int)((param[1]-_0)*kX/1000+25-4),(int)(HEIGHT-40-0.5*320-4),(int)((param[1]-_0)*kX/1000+25+4),(int)(HEIGHT-40-0.5*320+4));
}
|