Реферат: Применение геометрического подхода в мембранной теории возбуждения

Геометрия, электричество, функции

В начале 60-х годов натриевая теория ПД стала общепризнанной. Однако ее экспериментальная база была очень узкой — аксон кальмара. Поэтому в разных лабораториях мира начали изучать применимость этой теории к другим биологическим объектам. В большинстве случаев оказывалось, что самые разные возбудимые клетки — нервные волокна лягушки и кошки, мышечные волокна и др.— работают так же, как аксон кальмара.

Загадка миокардиальных клеток и «геометрический подход»

Одним из удивительных исключений оказались клетки сердца млекопитающих. Сначала и там все было в порядке. Швейцарский физиолог С. Вайдман изучал волокна Пуркинье проводящей системы сердца, которые передают сигнал от специальной структуры, лежащей на границе предсердия и желудочка, к мышечным клеткам желудочка. Эти волокна образованы «колонкой» клеток, соединенных высокопроницаемыми контактами. Вайдман показал, что в этих сердечных клетках быстрый подъем потенциала при возбуждении связан с открыванием натриевых каналов. Скорость нарастания ПД и его амплитуда зависели от содержания ионов натрия в наружном растворе, а сопротивление мембраны на пике ПД падало примерно в 100 раз по сравнению с состоянием покоя. Все было очень похоже на аксон кальмара.

Однако в случае клеток предсердия и желудочка ситуация оказалась совершенно иной и весьма неожиданной. И там амплитуда ПД зависела от концентрации ионов Ка⁺ в растворе, а ее значение составляло примерно 4-20 мВ; это означало, что проницаемость мембраны для 1Ча⁺ становилась примерно на порядок больше, чем для калия. Однако входное сопротивление ткани при возбуждении не менялось!

Этот факт прямо противоречил существующим взглядам. Для его объяснения придумывали разнообразные искусственные конструкции. Например, предполагали, что в сердечных клетках есть особые калиевые каналы, которые закрываются при деполяризации точно с той же скоростью, с какой натриевые открываются. В результате сопротивление не меняется. Но доказать существование таких быстрозакрывающихся каналов не удавалось. Неудачными оказывались и другие варианты объяснений.

В это время два биофизика С.А. Ковалев и Л. М. Чайлахян занимались еще одной задачей, казалось бы, не имеющей никакого отношения к сердцу. Они выясняли, как будет распространяться возбуждение по неоднородному нервному волокну. Вспомните, что в гл. 6 для простоты рассматривается бесконечный цилиндрический кабель, т. е. идеализированное однородное волокно. Но реальные нервные волокна могут расширяться и сужаться, практически все они ветвятся и обязательно где-то кончаются. Задача состояла в том, чтобы выяснить, что будет с нервным импульсом, когда он подойдет к области неоднородности — утолщению или мосту ветвления. Для таких случаев теории тогда не существовало.

Размышляя о ветвящихся волокнах, Ковалев и Чайлахян выдвинули совсем новую гипотезу для объяснения загадки сердечных клеток. Они рассуждали так. В проводящей системе сердца все происходит, как в аксоне кальмара, а в желудочке совсем иначе. Но проводящая система отличается от желудочка, прежде всего геометрической структурой: проводящая система образована волокнами, похожими на аксон дождевого червя,— они сходны с кабелем; желудочек, напротив, образован сложной сетью клеток, связанных высокопроницаемыми контактами, и никак не может считаться кабелем. Может быть, для объяснения необычного поведения желудочка не нужно искать какие-то необычные ионные каналы, но необходимо учесть эти геометрические различия?

Для ответа на этот вопрос надо было иметь для геометрически разных структур такую же теорию, как для однородного волокна.

С.А. Ковалев и Л.М. Чайлахян работали в Теоретическом отделе Института биофизики АН СССР, организованном в начале 60-х годов Г.М. Франком и И. М. Гельфандом. В нем собрались молодые математики, физики и биологи. Объединение разных знаний очень помогало в работе. Такое содружество и привело к тому, что в Теоретическом отделе было разработано обобщение кабельной теории, и в конце концов возник новый подход к возбудимым тканям, который для краткости назвали геометрическим.

В чем суть геометрического подхода? Свойства нервных и мышечных клеток во многом определяются свойствами их мембран. Эти свойства, в свою очередь, определяются тем, какие ионные каналы находятся в мембране. Однако, как оказалось, у природы есть и другой способ менять свойства клеток — менять их форму.

В биологии есть очень древняя проблема, которую называют проблемой формы и функции. Например, форма конечности у крота приспособлена для рытья земли, у летучей мыши — для полета, а у обезьяны — для хватания. С другой стороны, форма тела столь далеких по происхождению организмов, как древний ящер — ихтиозавр, рыба — тунец и млекопитающее — дельфин, весьма сходна, так как все они быстрые пловцы.

Геометрический подход — это фактически применение той же идеи к возбудимым тканям. Его основной принцип состоит в том, что свойства возбудимых клеток и тканей, а значит, и выполняемые ими функции во многом определяются их геометрической структурой: формой клеток, соотношением их размеров, взаимным расположением и связями.

Геометрический подход в электрофизиологии сейчас широко распространен и кажется вполне естественным: ведь поведение, например, нейрона существенно зависит от распределения потенциала на его мембране и от токов, которые текут в клетке и в окружающей ее среде. Но токи и напряжения, в свою очередь, зависят от распределения сопротивлений и емкостей, а это распределение определяется формой клетки. Эти простые соображения оказались очень продуктивными при применении к конкретным биологическим задачам. И дальше мы рассмотрим несколько примеров применения такого геометрического подхода к нервным клеткам, которые могут иметь разные размеры и форму, к нервным волокнам — аксонам и дендритам, — которые тоже не всегда сходны с проводом постоянного диаметра, и к клеточным системам.

О шаре и цилиндре

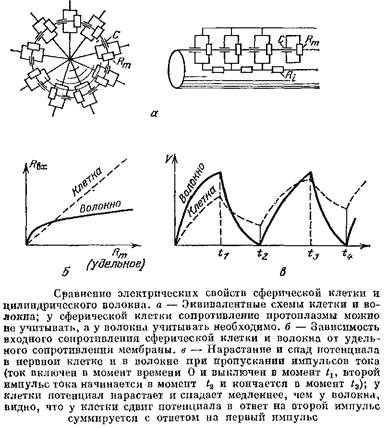
Сравним электрические свойства тела нервной клетки и нервного волокна, считая тело клетки шаром, а волокно — бесконечным цилиндрическим кабелем.

Сравнение электрических свойств шара и цилиндра, образованных одинаковыми мембранами, покажет нам, какую важную роль в определении этих свойств играет форма.

Электрические параметры, которыми характеризуются клетки и ткани, можно разделить на две группы. К первой группе относятся параметры, характеризующие вещество мембраны и протоплазмы: удельное сопротивление мембраны, которое обычно равно 1—10 кОм-см² , ее удельная емкость, обычно равная 1 мкФ/см² , и, наконец, удельное сопротивление протоплазмы, которое равно примерно 100 Ом-см. Эти параметры, естественно, не зависят от формы и размеров клетки.

Ко второй группе относятся параметры, которые называют системными. Они характеризуют клетку, волокно или систему связанных клеток в целом и зависят от размеров и формы. Один из основных системных параметров — это так называемое входное сопротивление, о котором нам уже приходилось говорить в гл. 6.

Входное сопротивление измеряется так. Один микро-электрод вводится в одиночную клетку, в волокно или в одну из клеток, электрически связанных с соседями, другой полюс при этом помещают в наружную среду и пропускают между ними ток /. Одновременно с этим второй микроэлектрод вводят в ту же одиночную клетку, волокно или клетку-соседа. Тогда при пропускании тока второй микроэлектрод будет регистрировать сдвиг МП А7, Второй микроэлектрод вводят возможно ближе к токовому электроду, поскольку, как мы знаем, в нервном волокне сдвиг потенциала будет убывать по мере удаления от токового электрода. Входным сопротивлением называют отношение сдвига потенциала к пропускаемому току!

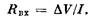
Таким образом, входное сопротивление — это аналог обычного сопротивления участка цепи. Естественно, что Л_вх клеток зависит от параметров первой группы и от формы и размеров клеток, а также их взаимного расположения. Например, как мы видели в гл. 6 ), входное сопротивление аксона выражается формулой

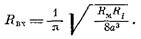
Здесь Л_ш и НI — удельные сопротивления мембраны и протоплазмы аксона, т. е. параметры первой группы; все остальное в формуле определяется геометрией волокна — предполагалось, что это цилиндр, у которого длина гораздо больше радиуса.

А теперь посмотрим, что будет, если из того же материала сделать другое «платье» — сферическую клетку радиуса а.

Можно показать, что у сферических клеток, даже у очень крупных, с диаметром порядка 1 мм, сопротивление протоплазмы составляет только 0,1% сопротивления мембраны. У клеток меньших размеров — а таковы все клетки в нервной системе позвоночных — сопротивление протоплазмы можно вообще не учитывать. Так что реально входное сопротивление сферической клетки зависит только от удельного сопротивления ее мембраны и от ее радиуса а:

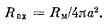
Сравним теперь формулы и. У сферической клетки Явх прямо пропорционально Я_м , поэтому если при возбуждении клетки удельное сопротивление мембраны уменьшится, например, в 36 раз, то и 7?_вх уменьшится тоже в 36 раз. У волокна же Л_вх пропорционально не Д_м , а только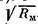, поэтому если при возбуждении сопротивление мембраны уменьшится также в 36 раз_Л то /?_вх изменится только в 6 раз.

Сферическая клетка и цилиндрическое волокно существенно отличаются и по своим емкостным свойствам. Если на сферическую клетку подействует постоянный ток_г

включенный в некоторый момент времени, то потенциал на ней будет нарастать по закону

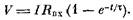
Если теперь ток выключить, то развившийся потенциал не исчезает мгновенно, а спадает со временем тоже экспоненциально:

Совсем другими емкостными свойствами обладает цилиндрическое волокно. Формулы для нарастания и спада тока становятся довольно сложными, и мы их приводить здесь не будем. Суть дела состоит в том, что при тех же самых свойствах мембраны, что и у сферической клетки, потенциал в кабеле и нарастает, и спадает гораздо быстрее.

Ну и что? Первые примеры влияния геометрии на функции

Какое значение имеют эти системные свойства для работы нейронов и волокон? В чем проявляется их различие? Приведем несколько примеров, показывающих важное значение системных параметров для работы нейронов.

Пример первый. Пусть у нас есть две сферические клетки — большая и маленькая, и на обеих клетках имеются одинаковые синапсы. Спрашивается, какое влияние окажут эти синапсы на разные клетки?

Формула для сдвига потенциала, вызываемого в клетке воздействием синапса — постсинаптического потенциала:

. Там же мы указывали, что И_с

очень велико и равно примерно 10¹² Ом. Входное сопротивление нейронов гораздо меньше: у нейрона диаметром 1 мм оно порядка 10⁸ Ом и даже у маленького нейрона диаметром всего 10 мкм оно составляет только 10⁹ Ом. Следовательно, в знаменателе вышеприведенной формулы /?вх мало по сравнению с И_с и им можно пренебречь. Мы получаем упрощенную формулу

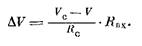
Как видно из этой формулы, постсинаптический потенциал, создаваемый одинаковыми синапсами в разных клетках, будет прямо пропорционален их /?_вх , а /?_вх сферической клетки, в свою очередь, обратно пропорционально квадрату ее диаметра. Так что при одинаковом воздействии постсинаптический потенциал в клетке диаметром 10 мкм будет в 100 раз больше, чем в клетке диаметром в 100 мкм. Об этой разной восприимчивости к синаптическим воздействиям клеток разного диаметра известный советский ученый М.М. Бонгард сказал: «Это понятно. Спичкой можно зажечь тонкую хворостинку, но нельзя зажечь бревно».

Пример второй. Когда мы разбирали механизм действия тормозных синапсов, то говорили, что они открывают ионные каналы для калия или хлора, что приводит к гиперполяризации клетки, удалению ее потенциала от порогового значения. Теперь мы можем указать вторую причину их тормозного действия. Открывая ионные каналы, тормозные синапсы снижают сопротивление мембраны, а тем самым и Я_вх нейронов. Из формулы видно, что эффективность действия возбуждающих синапсов тем меньше, чем меньше Я вх, поэтому тормозные синапсы, снижая Я_вх , снижают эффективность воздействия возбуждающих синапсов.

Но Д_В х сферической клетки и цилиндрического волокна, как видно из формул и, по-разному зависят от сопротивления мембраны. Если тормозные синапсы вдвое снизят сопротивление мембраны сферической клетки, то и Я вх, а значит, и эффективность возбуждающих синапсов тоже снизятся вдвое. Когда же тормозные синапсы действуют на цилиндрический кабель, например на длинный дендрит, результат будет иным: если сопротивление мембраны тоже снизится вдвое, то Я _вх снизится только в У 2, т е. примерно в 1,4 раза, а значит, и эффективность торможения будет меньше, чем в случае сферической клетки. Отсюда понятно, почему в организмах тормозные синапсы чаще встречаются на телах нейронов.

Пример третий. Мы видели, что один синапс создает на клетке, даже на очень маленькой, сдвиги потенциала, меньшие порога возбуждения в сотни и даже в тысячи раз. Отсюда следует, что клетка может возбудиться только в результате действия на нее не одного, а многих синапсов.

Когда на клетку примерно одновременно действует много синапсов, находящихся на разных участках ее мембраны, и их действие суммируется, этот процесс называют пространственной суммацией. Однако, как правило, разные синапсы срабатывают неодновременно: один уже кончил действовать, когда другой только начинает. В этом случае процесс называют пространственно-временной суммацией. Чисто временная суммация возникает при действии одного и того же синапса, если к моменту его последующего срабатывания сдвиг потенциала, созданный предыдущим срабатыванием еще не исчез.

Для временной и пространственно-временной суммации очень важно, насколько долго сохраняется «след» от синаптического воздействия, а это зависит от емкостных свойств нейрона. Если возникший потенциал спадает достаточно медленно, то действие второго синапса, включившегося позднее, может суммироваться с остаточным потенциалом от первого. В противном случае суммируется только действие тех синапсов, которые сработали практически одновременно.

Из рис. 43,в ясно, что потенциал в кабеле спадает гораздо быстрее, чем в сферической клетке. Но у беспозвоночных животных синапсы находятся не на телах нервных клеток, а на их отростках, т. е. именно на волокнах, обладающих свойствами кабеля. Отсюда следует, что при одних и тех же свойствах мембраны синаптические потенциалы у беспозвоночных будут суммироваться в меньшей мере, чем на тех нейронах позвоночных, где синапсы находятся на телах клеток. Если же синапсы у позвоночных расположены на длинных дендритах, то суммация будет идти так же, как у беспозвоночных.

Мы рассмотрели две простейшие структуры: сферическую клетку и цилиндрическое волокно. Дальше мы рассмотрим несколько более сложных примеров влияния формы клеток и топологии ткани на их электрические свойства и функции.

Нервное волокно расширяется, сужается, ветвится и кончается

В 1964 г. в Ереване проходил очередной Всесоюзный физиологический съезд. Один из авторов этой книги докладывал на съезде первые результаты и программу исследований, связанных с геометрическим подходом. Среди слушателей был Б.И. Ходоров, сотрудник института хирургии им. А.В. Вишневского, в дальнейшем много сделавший для развития и пропаганды такого подхода. Но тогда он сильно усомнился в правильности выводов, сделанных в докладе о распространении импульсов по неоднородным нервным волокнам, и решил проверить их самостоятельно. Многие выводы этого доклада были сделаны на основании только качественного рассмотрения, так сказать, «на пальцах». Б.И. Ходорсн решил проверить их количественно. Так появилась первая машинная модель проведения импульсов по неоднородным нервным волокнам. Что же удивило Ходорова?

Представим себе, что нервное волокно в некоторой точке резко расширяется. Что произойдет с импульсом, идущим из тонкого участка в толстый? Когда импульс идет по тонкой части волокна, ток, создаваемый возбужденным участком, заряжает мембрану, лежащую рядом с возбужденной областью, и идет по аксоплазме в более удаленные участки. По мере приближения возбужденной области к месту расширения все большая доля тока начинает перетекать в широкую часть волокна — ведь там меньше сопротивление — и меньшая доля тока идет через мембрану невозбужденной области узкого участка волокна. Из-за этого емкость мембраны узкого участка заряжается медленнее, потенциал нарастает медленнее, и импульс замедляет свое движение. Кроме того, снижается и амплитуда импульса, так как при медленном нарастании потенциала успевает инактивироваться часть натриевых каналов.

Пусть теперь импульс подошел вплотную к месту расширения. Условия проведения еще более ухудшаются: ток генерируется мембраной узкой части, а возбудить должен большую по площади мембрану толстой части. Ток, идущий через мембрану широкой части, растекается по большой площади и медленно заряжает ее емкость. В результате потенциал в широкой части волокна будет нарастать очень медленно.

На основании таких соображений авторы доклада и сделали предсказание, что перед расширением импульс должен замедляться и снижать амплитуду, а при некотором критическом расширении вообще не сможет пройти через эту область. Вот эти предсказания и были проверены Б. И. Ходоровым и его сотрудниками с помощью расчетов на вычислительной машине.

Расчеты полностью подтвердили все предсказания. Оказалось, что при расширении волокна в 6 раз ПД не может пройти через это расширение. Шестикратное расширение является критическим, если мембрана волокна точно такая, как у гигантского аксона кальмара; если же эта мембрана более «низкого качества», то блокирование возникает при меньших расширениях.

В дальнейшем задачей о круто или постепенно расширяющихся и сужающихся волокнах занимались многие теоретики и экспериментаторы. Так, сотрудникам Института электрохимии АН СССР В.С. Маркину и Ю.А. Чизмаджеву удалось решить задачу о распространении ПД в волокне с расширением без вычислительной машины, с помощью несколько упрощенной математической модели. Они получили очень неожиданный результат. Оказалось, что если окружить волокно плохо проводящей средой, то ПД может пройти через большее расширение, т. е. если ухудшить условия распространения импульса, то преодоление препятствия облегчается! В чем же тут дело? Грубо говоря, дело в том, Что при увеличении внешнего сопротивления убывает константа длины волокна, и ток не растекается далеко в широкую часть волокна, что облегчает преодоление препятствия.

А что будет, если волокно не расширяется, а, напротив, сужается? Повторив рассуждения о расширяющемся во* локне, так сказать, «со знаком минус», легко сообразить, что по мере приближения ПД к месту сужения его скорость должна нарастать, а амплитуда увеличиваться. Это явление оказалось очень важным — ведь к нервным волокнам вполне применима поговорка: «Сколько веревочке ни виться...». Всякий аксон, в конце концов, оканчивается, причем тонкими терминалями, получается как бы «сужение до нуля». Значит, при подходе к терминали импульс все более разгоняется, его амплитуда растет. Возникает явление, похожее на гидравлический удар, когда текущая по трубе жидкость натыкается на препятствие. Возрастание амплитуды потенциала в конце терминали очень важно для работы химических синапсов, так как улучшает условия выделения медиаторов.

Рассмотрим теперь явления в области ветвления нервного волокна.

У позвоночных животных ситуация в области ветвления аксона, как правило, не отличается от случаев расширения и сужения волокна, так как импульс у них возникает в теле клетки и всегда идет от тела по аксону. Если импульс подходит к точке ветвления по толстому стволу, который делится на две тонкие веточки, то ПД перед точкой ветвления ускоряется. Если же площадь мембраны выходных веточек волокна больше, чем у той веточки, по которой приходит импульс, то ПД около точки ветвления замедляется и может даже заблокироваться.

В нейронах беспозвоночных в области узлов ветвления может возникать совсем иная ситуация. Дело в том, что у них, как уже говорилось, синапсы располагаются не на теле нейрона, а на разных веточках отростка нервной клетки, так что эти веточки могут возбуждаться независимо друг от друга. Представим себе узел ветвления, в котором две тонкие веточки и одна более толстая. Соотношение их диаметров может быть таким, что ПД не проходит в толстую веточку ни из одной тонкой, когда они возбуждаются по отдельности, но проходит в том случае, когда ПД возникает сразу в обеих тонких веточках и подходит к месту ветвления более или менее одновременно. Такой узел ветвления работает как схема совпадений или логический элемент «И»: импульс за узлом ветвления возникает только тогда, когда имеют место два события одновременно, и отсутствует, если возникает только одно из них. Нейроны, работающие по этому принципу, были действительно обнаружены у некоторых моллюсков.

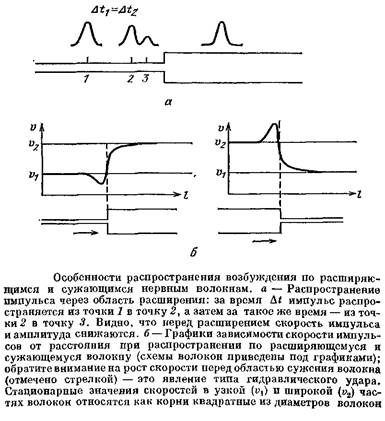
С помощью узлов ветвления такого «логического» типа, в принципе, в нервной системе может быть образовано много разных устройств. Например, легко представить себе нейрон, который обнаруживает источник звука, расположенный прямо впереди животного;

сигналы от него будут приходить к ушам одновременно. В качестве другого примера рассмотрим «детектор однонаправленных движений». Пусть имеется нейрон со структурой дендрита, как на рис. 45. Пусть на каждую его веточку действует, например, фоторецептор. Если световой стимул пробегает по фоторецепторам слева направо, то поочередно возбуждаются веточки 2, 2„ 3 и т. д. Когда ПД от веточки / приходит к первому узлу! туда же подходит сигнал от веточки 2_г происходит их суммация, импульс преодолевает «логический» узел и идет дальше. У следующего узла встречаются этот импульс и ПД от веточки 3 и т. д. Если же стимул движется в противоположном направлении, то импульс от веточки 5 затухнет, так как к нему «на подмогу» не придет импульс от веточки 4.

Такое устройство будет возбуждать тело клетки только в том случае, когда стимул движется по сетчатке в определенном направлении и с определенной скоростью; на другие сигналы нейрон отвечать не будет.

Заметим, что, поместив в область узла ветвления возбуждающие или тормозные синапсы, можно управлять процессом прохождения ПД через узел.

Зачем нейрону дендриты, а дендритам шипики

Многие нервные клетки похожи на кусты или деревья: их выходной отросток, аксон, — тонкий корешок этого дерева, все остальные многочисленные отростки — дендриты. Дендриты обычно отходят от тела клетки в виде толстых стволов, которые затем делятся на несколько более тонких ветвей, те, в свою очередь,— на еще более тонкие и т. д. Длина дендритов в десятки раз превышает диаметр нервных клеток, а толщина концевых веточек очень мала — может составлять доли микрометра. Вопрос о том, какую роль играют дендриты в работе нервных клеток, до сих пор окончательно не решен и, скорее всего, у разных нейронов их роль различна. В частности, у одних клеток мембрана дендритов невозбудима и может передавать сигналы только электротонически, как пассивный кабель, а у других — дендриты способны проводить ПД. Сейчас мы рассмотрим только те свойства дендритов, которые связаны с их геометрией.

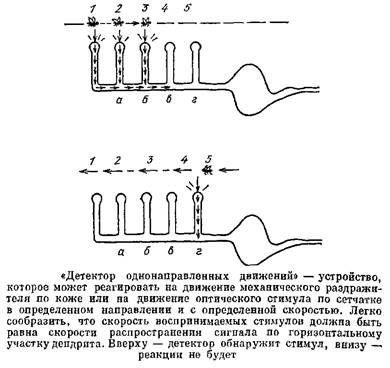
Рассмотрим сначала те клетки, у которых дендриты невозбудимы. В этом случае «проблема дендритов» состоит в следующем. Синаптические окончания встречаются на самых разных частях дендритного дерева. Возьмем синапс, действующий на веточку, максимально удаленную от тела клетки. В этом случае условия для передачи электрического сигнала представляются весьма невыгодными. Действительно, в тонкой веточке велика константа затухания, а своим концом веточка «впадает» в более широкий участок дендрита, который «закорачивает» ее. В таких закороченных кабелях потенциал спадает особенно сильно, правда, в случае дендритов «закорачивание» является неполным и потенциал в конце веточки спадает не до нуля. В следующем отрезке дендрита условия для передачи сигнала тоже неблагоприятные, так как на его конце тоже находится более толстый дендритный ствол, и т. д. « В связи с этим возникло представление, что синапсы, расположенные на удаленных веточках, дают очень малый вклад в изменение потенциала тела клетки, в сотни раз меньший, чем такие же синапсы на теле клетки. Получается, что синапсы на конечных дендритных веточках бесполезны, что это «ошибка природы».

Один из вариантов решения «проблемы дендритов» состоит в том, что на тонких концевых веточках можно разместить много синапсов, тогда совместное действие этих синапсов будет заметно в теле клетки. Но для этого надо, чтобы все эти синапсы работали более или менее одновременно.

Все вышеприведенные рассуждения долгое время носили качественный характер. В 1965 г. в Теоретическом отделе Института биофизики АН СССР был разработан способ количественной оценки эффективности синапсов для нервных клеток любой формы и рассчитана эта эффективность для мотонейронов, пирамидных клеток коры и клеток мозжечка. Оказалось, что эффективность дендритных синапсов всего в 3—5 раз ниже, чем у синапсов, расположенных на теле нейрона. Чем это объясняется? Почему эффективность удаленных дендритных синапсов оказалось довольно велика? Чем меньше клетка, чем выше ее входное сопротивление, тем больший сдвиг потенциала создает синапс. У тоненьких дендритных веточек, удаленных от тела клетки, входное сопротивление оказалось большим, поэтому синапсы могут создавать в этих веточках сдвиги потенциала в десятки раз большие, чем в теле нейронов. И хотя при распространении к телу этот сдвиг потенциала действительно сильно затухает, его большая величина в значительной мере компенсирует затухание. Таким образом, дендритные синапсы оказались вовсе не ошибкой природы.

А теперь рассмотрим те нейроны, дендриты которых обладают возбудимой мембраной, способной к генерации ПД, У таких нейронов высокая эффективность синапса на тонкой веточке может привести к тому, что всего несколько синапсов доведут мембранный потенциал до порога и вызовут в этой веточке ПД, который начнет распространяться к телу клетки.

Его дальнейшая судьба зависит от свойств узлов ветвления, через которые ему надо пройти по пути к телу клетки, т. е. от геометрии дендрита. Клетка такого типа работает как сложная логическая схема. Пример такой клетки был приведен на рис, 45; эта клетка обнаруживает однонаправленные движения стимула. Клетки с более сложной формой дендритов могут работать как довольно хитрые вычислительные машины. «Такая система подобна системе голосования с большим числом участников, которые имеют неодинаковое число голосов... Окончательный результат, конечно, зависит от общего числа голосов, поданных «за» или «против», однако он в не меньшей степени зависит и от того, кто именно и вместе с кем из партнеров голосует»,— писали сотрудники Теоретического отдела Института биофизики АН СССР в 1966 г.

На дендритах многих нейронов имеются особые образования, так называемые шипики. Это структуры, похожие на грибы и состоящие из головки на тонкой ножке, которую чаще называют шейкой шипика. Шипик представляет собой выпячивание клеточной мембраны, а к его головке подходит терминаль от другого нейрона и образует на ней химический синапс.

Зачем нужны шипики — неизвестно. Число гипотез об их функциях огромно. Давайте посмотрим, что можно сказать о возможных функциях шипиков, исходя из геометрических соображений. При этом рассмотрим два ра-рианта: мембрана головки шипика невозбудима; мембрана головки шипика способна к генерации ПД.

Пусть шипик невозбудим. Его тоненькая шейка имеет высокое сопротивление. В результате в головке будет возникать большой постсинаптический потенциал, но его заметная часть будет теряться в шейке. Шипик будет работать как тоненькая дендритная веточка. Но зачем нужно такое устройство? Почему бы синапсу не располагаться прямо на дендрите?

Одним из способов работы тормозных синапсов является снижение входного сопротивления нейрона. Но ведь и возбуждающие синапсы тоже открывают ионные каналы и снижают входное сопротивление! Из-за этого возбуждающие синапсы тоже мешают друг другу. Особенно сильна такая помеха будет на тонких дендритах, у которых очень высоко входное сопротивление, так что активация нескольких синапсов вызовет заметное его снижение. Шипики должны существенно снижать взаимное влияние соседних синапсов, которые в этом случае отделены друг от друга шейками с высоким сопротивлением. Расчеты подтвердили, что хотя шипиковые синапсы каждый по отдельности менее эффективны, чем синапсы, расположенные прямо на дендрите, но при совместной работе эффект заметно выше.

Если же мембрана шипика возбудима, то он может работать как усилитель синаптической передачи. Из-за тонкости шейки входное сопротивление шипика очень велико и один синапс может вызвать в головке ПД, который пошлет в дендрит гораздо более сильный электрический ток, чем ток синапса. Интересно, что при таком режиме работы шипика должно существовать оптимальное сопротивление его шейки. Оно не должно быть слишком маленьким — тогда заметная часть синаптического тока будет утекать в дендритную веточку, сдвиг потенциала на мембране головки шипика не достигнет порогового значения и там не возникнет ПД. Но, с другой стороны, сопротивление шейки шипика не должно быть и слишком большим, иначе из головки шипика в дендрит будет течь слишком слабый ток и никакого усиления синаптического тока не получится. Недавно появились работы, показывающие, что геометрическая структура реальных шипиков близка к той,, которая по теоретическим расчетам является оптимальной.

До сих пор мы говорили о форме волокон и клеток или даже микроструктур клеток — шипиков. Посмотрим теперь на геометрию клеточных объединений.

Геометрическое выпрямление

Разберем сначала самый простой случай: пусть есть две клетки, соединенные между собой ЭС. Действие ЭС, в отличие от действия ХС, симметрично, И действительно, сам ЭС — это система тонких отверстий, которые совершенно одинаково пропускают ток в обе стороны. А вот действие такого синапса на связанные им клетки может сильно различаться, если эти клетки отличаются по величине, а значит, и по входному сопротивлению.

Пусть ЭС связывает две клетки — большую и маленькую. Пусть в какой-то из них возник сдвиг потенциала Д7_Х . Этот сдвиг потенциала делится на две части — падение напряжения на сопротивлении ЭС и падение напряжения АУ₂ на Д₂ второй клетки, причем в соответствии с законом Ома потенциал распределяется пропорционально сопротивлениям участков. А отсюда сразу следуют важные выводы. Пусть,, например, Л₂ первой клетки примерно в 9 раз меньше Л_к , а -К₂ второй клетки только в 4 раза меньше Л_к - Если возбудилась первая клетка, то ее ПД, равный примерно 100 мВ, разделится в отношении 1:4, т. е. на второй клетке возникнет сдвиг потенциала около 20 мВ, и эта клетка возбудится, так как пороговое значение обычно равно примерно 15 мВ. Однако если такой же ІІД в 100 мВ возникнет во второй клетке, то он разделится в отношении 1: 9, тогда на долю первой клетки придется только одна десятая часть его, т, е. 10 мВ, что ниже порогового значения.

Получается, что ПД может передаваться через ЭС только в одном направлении. За счет разных размеров клеток возникает эффект, который называют геометрическим выпрямлением.

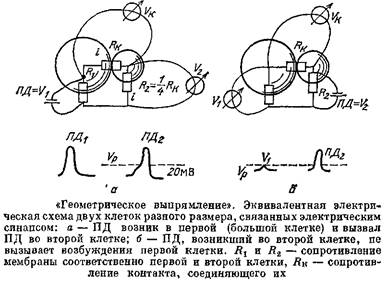
Но высокое и низкое Лвх зависит не только от размеров клеток. Пусть обе клетки однинаковы, но на одну из них подействовали химические синапсы, повысили проводимость ее мембраны, а это все равно, что сделали клетку большой. Таким образом, ХС могут регулировать работу ЭС и делать передачу через них односторонней.

Такая система регуляции существует, например, у некоторых моллюсков. Она управляет работой мышц их глотки. При необходимости схватить добычу моллюск делает резкое движение, все мышцы сокращаются одновременно» втягивая добычу. При этом все мотонейроны, управляющие мышцами, связаны ЭС, поэтому ПД в них возникает одновременно. При жевании те же мышцы должны работать неодновременно; это достигается тем, что под действием ХС Л_вх мотонейронов снижается и ПД в одной клетке теперь уже не может возбудить другие.

Разгадка сердечной загадки

Необычное поведение миокарда: входное сопротивление в нем не меняется при возбуждении. Как оказалось, такое поведение миокарда объясняется не особенностями мембран сердечных клеток, а его собственной геометрией.

Клетки сердца соединены между собой многочисленными ЭС и образуют сложную сетку, так называемый синцитий.

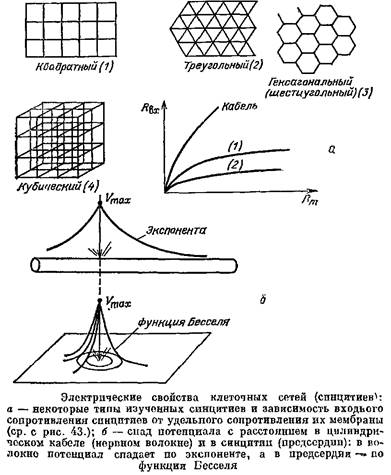
Для того чтобы выяснить электрические свойства синцитиев, надо было обобщить кабельную теорию и на этот случай. В качестве моделей миокарда были выбраны правильные сети. Отрезки кабеля между узлами моделировали миокардиальные клетки, а вся сеть, имеющая общий непрерывный сердечник и общую изоляцию, имитировала миокард. Основы математической теории таких синцитиев были созданы сотрудником Теоретического отдела Института биофизики АН СССР В.В. Смоляниновым, который впоследствии написал одну из первых книг о геометрическом подходе к возбудимым тканям.

Электрические свойства синцитиев оказались во многом необычными. Выяснилось, в частности, что Лвх синцитиев очень слабо зависит от сопротивления мембраны их клеток. Если даже*сопротивление мембраны упадет в 100 раз, то Я_вх изменится так мало, что это изменение не удастся обнаружить в эксперименте. Зато Я_вх синцитиев сильно зависит от сопротивления протоплазмы.

Зависимость Н_вх геометрически разных структур от удельного сопротивления мембраны и удельного сопротивления протоплазмы.

Сравним теперь, как меняется мембранный потенциал в геометрически разных объектах по мере удаления от точечного источника тока. В сферической клетке сдвиг потенциала одинаков в любой точке ее мембраны — она эквипотенциальна. В цилиндрическом волокне потенциал спадает по экспоненте, а в синцитии потенциал спадает гораздо круче, чем по экспоненте; например, спад потенциала в таком почти плоском тонком синцитии, как предсердие лягушки, описывается функцией Бесселя.

Крутой спад потенциала в синцитиях позволяет, хотя fot на качественном уровне, объяснить, почему их /?_вх так рлабо зависит от сопротивления мембраны. Пусть мы измеряемR_BX ,пропуская ток между некоторой точкой синцития и наружной средой. Большая часть этого тока вытекает через область синцития, лежащую в некоторой окрестности точки пропускания тока; назовем эту область синцития эффективной. Пусть теперь сопротивление мембраны клеток синцития снизилось. От этого убывает константа длины волокон синцития. Потенциал спадает в каждом волокне круче, и площадь эффективной области синцития убывает. Практически эта площадь уменьшается примерно во столько же раз, во сколько раз снижается сопротивление мембраны. А так как сопротивление эффективной области тем меньше, чём меньше удельное сопротивление мембраны, и тем больше, чем меньше площадь эффективной области, то в результате влияние этих факторов взаимно компенсируется и Д_вх практически не меняется. Кроме того, -Rexсинцитиев очень мало по сравнению сR_BX клетки или волокна с такой же мембраной. Это естественно: ток, инъецируемый в данную точку синцития, растекается по его разветвленным отросткам во все стороны и вытекает наружу через большую поверхность.

Синцитии имеют и другие особенности: например,, в сердце сдвиг потенциала спадает во времени примерно на порядок быстрее, чем в сферической клетке с такими же свойствами мембраны, а значит, гораздо быстрее, чем в кабеле. Все эти особенности синцитиев имеют важное функциональное значение. Так, синцитиальные ткани очень «помехоустойчивы». Из-за низкого входного сопротивления один или несколько синапсов, действующих на такую ткань, будут оказывать очень слабый эффект. Если одна клетка сердца заработает вдруг с высокой частотой, то эта «взбесившаяся клетка» не сможет повлиять на ритм всего сердца: она одна не в состоянии возбудить соседние клетки синцития. Чтобы существенно повлиять на работу синцитиальной ткани, надо подействовать одновременно на многие клетки синцития, т. е. воздействие должно быть не точечным, а распределенным. Тогда соседние клетки будут в равных условиях, ток из одной клетки не будет утекать в соседние и эффект будет такой же_л как при воздействии на изолированную клетку. И действительно, в синцитиальных тканях, например в гладких мышцах кишечника, нервные волокна очень широко разветвлены и действуют сразу на многие клетки.

Итак, загадка миокарда оказалась разгаданной. Она оказалась результатом неудачно поставленного вопроса. В данном случае ученые рассуждали по аналогии: «В клетке при возбуждении входное сопротивление падает? Падает. В волокне при возбуждении входное сопротивление падает? Падает. Значит, и в синцитии при возбуждении входное сопротивление должно падать». А оказывается, не должно. При изменении размерности объекта электрические свойства могут качественно меняться.

Одномерный, двумерный, трехмерный

Нервное волокно, у которого длина намного больше диаметра, можно считать одномерной возбудимой средой, тонкую ткань предсердия — двумерной. Двумерные возбудимые ткани могут иметь разную топологию: например, у асцидий сердце представляет собой трубку, образованную одним слоем клеток; можно считать, что это двумерная возбудимая среда, образующая цилиндр. Синцитии, рассмотренные выше, топологически эквиваленты плоскости.

В «одномерном» нервном волокне импульс может идти только в одном направлении. В двумерных синцитиях возбуждение распространяется во все стороны, образуя фронт волны, подобно кругам на воде, разбегающимся от брошенного камня.

Такие волны возбуждения все время бегут по сердцу. Они возникают в специальном ведущем узле, пробегают по предсердию, а потом медленно ползут по синцитию, лежащему на границе между предсердием и желудочком. Эта «линия задержки» необходима, чтобы предсердие успело выбросить кровь в полость желудочка. Потом возбуждение переходит с «линии задержки» на проводящую систему, которая быстро возбуждает весь желудочек.

Форма фронта волны в возбудимых средах, как и в случае обычных физических волн, зависит от скорости распространения возбуждения. Если среда изотропна, волны будут круговые. Но скорость возбуждения в синцитии сильно зависит от его геометрии; например, в таком синцитии,, как на рис, 49_г а, при распространении в горизонтальном направлении вдоль волокон скорость велика, а при распространении в вертикальном направлении токи в каждом узле ветвления перетекают в длинные боковые перемычки, и это снижает скорость проведения. Расчеты, проведенные на ЭВМ сотрудницей Института проблем передачи информации АН СССР Т.А. Шура-Бура, показали, что за счет такой организации сети скорость возбуждения может быть снижена на порядок. Такой анизотропный синцитий и образует «линию задержки» между предсердием и желудочком.

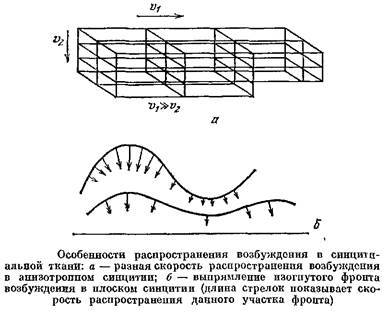
Свойства возбудимых тканей определяют и ряд других важных особенностей волн возбуждения. Например, если по синцитию идет волна с искривленным передним фронтом, то фронт сам собой выравнивается, так как вогнутые его участки распространяются быстрее, чем выпуклые. Другой пример: если механическая волна наталкивается на препятствие, она может отразиться и пойти обратно. С волной возбуждения такого случиться не может: сразу же за волной идет участок рефрактерности. Поэтому импульс, идущий по волокну, дойдя до его конца, исчезает.

Теперь представим себе, что у нас есть «кусок» двумерной возбудимой среды с отверстием. Пусть нам удалось запустить в нем волну возбуждения только в одном направлении, как показано на рис. 50, а. Если отверстие достаточно велико, то возбуждение, обойдя его и вернувшись в исходное положение, застанет ткань уже вышедшей из состояния рефрактерности и вновь побежит по тому же пути. Длина границы отверстия₁ очевидно, должна быть не меньше скорости волны, умноженной на длительность рефрактерного периода, тогда волна будет все время бегать по возбудимой среде.

Еще в начале нашего века была высказана гипотеза, что именно таким круговым движением волны объясняется опасное нарушение сердечного ритма — фибрилляция предсердий. По этой гипотезе круговая волна не дает распространяться обычной нормальной волне возбуждения и нарушает сокращения сердечной мышцы.

Изучением фибрилляции занимались многие ученые. Создатель кибернетики Н. Винер совместно с мексиканским физиологом А. Розенблютом предложили в 1946 г, первую математическую модель двумерной возбудимой среды и начали рассматривать разные режимы распространения возбуждения в ней. В этих первых моделях еще никак не учитывались физическая природа распространяющихся волн и свойства синцитиальных тканей. В начале 60-х годов И.М. Гельфанд и М.Л. Цетлин на своем физиологическом семинаре рассмотрели более сложную модель, приняв, что в такой возбудимой среде имеются клетки, способные самопроизвольно возбуждаться с разными периодами. Участник того же семинара И.С. Балаховский показал, что в двумерной возбудимой среде может возникнуть непрерывно крутящаяся спираль, даже если в среде нет отверстия.

Но особенно много интересных вещей о двумерных возбудимых средах и фибрилляции было выяснено в лаборатории Института биофизики АН СССР, которой заведует В.И. Кринский, начавший эти исследования еще будучи аспирантом Теоретического отдела. Об этих работах надо было бы рассказывать в отдельной книге. В работах Кринского. показано, что ревербераторы могут возникать, исчезать, а также порождать много новых ревербераторов и многое другое.

Если предсердие можно рассматривать как двумерную возбудимую среду, то ткань желудочка сердца, имеющего большую толщину, необходимо рассматривать как среду трехмерную. В таких средах возбуждение может вести себя еще сложнее. Сотрудники Кринского показали, например, что в такой среде вместо ревербераторов могут возникать «вихри» — структуры вроде баранок, в которых волны бегут, как на рис. б, и которые движутся в среде.

Роль формы дендритов нервных клеток начал изучать в США В. Ролл, влияние размеров и входного сопротивления мышечных клеток на возникающие в них синаптические потенциалы — Б. Катц в Англии, особенности геометрической структуры тканей сердца, важные для его функции,— физиологи Д. Вудбари и В. Крилл в США и австралийский математик Э. Джордж. Все эти работы велись в конце 50-х или начале 60-х годов. Все они содержали элементы геометрического подхода. Это означало, что необходимость нового подхода объективно созрела, что эта идея «витала в воздухе».

Со времени возникновения геометрического подхода прошло более четверти века. За это время он доказал свою жизнеспособность, на его основе написаны сотни статей и десятки книг в разных странах мира. И, встречая такую статью в новом номере журнала, мы вспоминаем школьное здание на Профсоюзной улице в Москве, где молодые биологи, физики и математики давно уже не существующего Теоретического отдела Института биофизики горячо обсуждали, что случится с нервным импульсом, когда оп подойдет к точке ветвления нервного волокна, и почему входное сопротивление сердечной ткани не меняется при ее возбуждении.