МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ АСТРАХАНСКОЙ ОБЛАСТИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
АСТРАХАНСКОЕ ПЕДАГОГИЧЕСКОЕ УЧИЛИЩЕ №1
КУРСОВАЯ РАБОТА
НА ТЕМУ:
«ФОРМИРОВАНИЕ ПРОСТРАНСТВЕННОГО МЫШЛЕНИЯ
ПРИ ИЗУЧЕНИИ ВЕКТОРНОГО ПРОСТРАНСТВА
У УЧАЩИХСЯ ОСНОВНОЙ ШКОЛЫ»
Выполнила: студентка гр. 3В
Джоржанова К.К
Проверила:
преподаватель алгебры
Никулина И.Е.
АСТРАХАНЬ 2006
СОДЕРЖАНИЕ
Введение
Глава I Теоретические основы формирования пространственного мышления у учащихся основной школы при изучении векторного пространства
1.1 Понятие пространственного мышления
1.2 Векторное пространство
1.3 Роль векторного пространства в формировании пространственного мышления учащихся основной школы
Глава II. Методика формирования пространственного мышления учащихся основной школы при изучении векторного пространства
2.1 Методические аспекты развития пространственного мышления как элемента образного
2.2 Методика формирования пространственного мышления учащихся основной школы при изучении элементов геометрии
2.3 Методика формирования пространственного мышления учащихся основной школы при построении модели к задачам
Заключение
Список литературы
Введение
Задача развития пространственного мышления учащихся основной школы имеет особую значимость, она должна с первых дней пребывания детей в школе, т. к. развитие мышления, а в особенности наглядно-образного и пространственного тесно связано с интеллектом человека. Человеческое существо с самого своего рождения погружено в социальную среду, которая воздействует на него в той же мере, что и среда физическая. Более того, подобно тому, как это делает физическая среда, общество не просто воздействует на индивида но непрестанно трансформирует самого его структуру, ибо оно не только принуждает его к принятию фактов, но и представляет ему вполне установившиеся системы знаков, изменяющиеся мышление индивида, предлагает ему новые ценности и возлагает на него бесконечный ряд обязанностей. Это позволяет сделать очевидный вывод, что социальная жизнь трансформирует интеллект через воздействие трёх посредников: языка (знаки), содержание взаимодействий субъекта с объектами (индивидуальные ценности) и правил, предписанных мышлению (коллективные логические или дологические нормы). (Пиаж, с. 213)
Реклама

Поэтому в настоящее время интерес к развитию мышления и как частного случая образно-пространственного мышления значительно возрос. Но он имеет недолгую историю. Проблеме пространственного мышления в последнее время в психологии стало уделяться значительно больше внимания, чем было раньше. Ему посвящены работы А. Н. Леонтьева, С. Д. Смирнова, А. Р. Лурия, А. А. Госпеева, В. М. Гордона, И. С. Якиманской, Е. Н. Кабановой-Меллер, М. В. Рыжика, Л. М. Фридмана и другие.
В них рассматриваются вопросы значения пространственного мышления человека для формирования понятий и для продуктивной деятельности, возрастные и индивидуальные особенности образного и пространственного мышления, возможности его при решении разнообразных проблем; приводятся феноменальные случаи образного, пространственного мышления, изучаются виды образов.
Психологами изучалось функционирование воображения и роль его в творческой деятельности человека, виды воображения и приёмы создания новых образов. Этому посвящены работы Л. С. Выготского, И. В. Страхова, О. Н. Дьяченко, Ц. П. Короленко, С. В. Фатеева и другие. В них подчёркивается связь воображения с целеполаганием, отмечается значение практической деятельности для его развития.
Философскому осмыслению образного мышления, выявлению значения знаков в познавательной деятельности человека, обсуждению связи и образу посвящены работы И. И. Мантатова, В. С. Тюхтипа, А. В. Славина, Н. Г. Салминой.
Большое значение в раскрытии механизмов создания образов, в выявлении закономерностей зрительного восприятия имеют работы по визуальному мышлению психологов Р. Арнхейма, И. Рока, Ж. Пиаже, В. В. Сташка, Р. Франсе и др.
Среди части педагогов математиков имеет осознание важности пространственного мышления в усвоении математики. Об этом можно найти явные или неявные высказывания у Ж. Адашора, А. Д. Александрова, Р. Куранта, Д. Пельберта, В. М. Тихомирова.
Различные аспекты пространственного мышления при изучении математики (от научно-популярных до методических разработок)исследовали Ю. П. Попов, Ю. В. Пухначёв, М. И. Башмаков, В. Г. Болтяский, С. Б. Вергенко, Г. Д. Глейзер, В. А. Далингер, Г. Н. Никитина, А. Пардала.
В настоящее время имеет место противоречие между наличием разработанных методов и приёмов формирования пространственного мышления в психологии и методике и отсутствием системы заданий, которая способствовала бы формированию пространственного мышления у учащихся начальной школы. Отсутствие такой системы является причиной низкого уровня сформированности у учащихся основной школы, а также у выпускников среднего звена, пространственного мышления, без которого нельзя говорить о полном развитии мышления учащихся.
Реклама

Отмеченное противоречие обуславливает актуальность выбранной темы исследования.
Цель настоящего исследования - разработать систему заданий, способствующих развитию пространственного мышления учащихся основной школы при изучении векторного пространства.
Задачи курсовой работы:
-изучить и проанализировать психолого-педагогическую, методическую литературу по данной проблеме;
-провести анализ состояния проблемы в практике;
-разработать и экспериментально проверить методику формирования пространственного мышления учащихся основной школы при изучении векторного пространства.
Для решения поставленных задач были использованы следующие методы: изучение работ психологов, педагогов, специалистов по методике преподавания математики; наблюдение за деятельностью учителей и учащихся при обучении математике; беседы с учителем и учащимся начальной школы; протоколирование уроков и их анализ; изучение письменных работ учащихся; тестирование.
Глава I Теоретические основы формирования пространственного мышления у учащихся основной школы при изучении векторного пространства
1.1 Понятие пространственного мышления
Прежде, чем говорить о пространственном мышлении и его сущности, необходимо понять что же такое мышление, какие его виды бывают каковы их особенности.
Известный советский психолог А. Н. Леонтьев обоснованно считал, что "жизненный, правдивый подход к воспитанию - это такой подход к отдельным воспитательным и даже образовательным задачам, который исходит из требований к человеку: каким человек должен быть в жизни и чем он должен быть для этого вооружён, какими должны быть его знания, его мышления, чувство и т. д. "[1]
. Следовательно, организуя и проводя обучение математике, необходимо всё время иметь в виду тот идеал человека, который создан обществом. Если мы с этой точки зрения посмотрим на задачи общего образования, и в частности на задачи школьного курса математики, то придём к выводу, что одной из первоочередных и важнейших задач является задача развития мышления учащегося.
Качества человека, формируемые в учебно-воспитательном процессе, делятся на общие и специальные. Мышление, конечно, относится к общим качествам, и его формирование происходит в процессе обучения всем учебным предметом, в процессе всей жизни учащихся.
Однако, общепризнанно и исторический опыт это подтверждает, что обучение математике в формировании мышления играет первостепенную и исключительно большую роль, в которой роль математики ещё более значительна. Вот что по этому поводу пишет академик В. В. Давыдов: "Решение конкретных задач современного школьного образования в конечном счёте связано с изменением типа мышления, проектируемого целями, содержанием и методами обучения. Всю систему обучения, необходимо переориентировать с формирования у детей рассудочно-эмпирического мышления на развитие у них современного научно-технического мышления"[2]
. Поэтому нужно установить, какой вклад в решение задачи формирования научно-технического мышления может внести обучение математике, как оно должно быть для этого организованно, каково должно быть его содержание и методы обучения.
Чтобы разобраться во всём этом, необходимо предварительно выяснить, в чём сущность мышления, каковы его особенности и виды, каким образом происходит процесс формирования мышления у детей.
С помощью мышления человек познаёт окружающий мир. Однако познание может осуществляться и без мышления, с помощью одних лишь органов чувств (чувственное познание), дающее человеку разного рода ощущения, восприятия и представления о внешнем мире. Чувственное познание является непосредственным, ибо оно осуществляется в результате прямого контакта человека, его органов чувств, с познаваемым объектом. Между тем мышление является опосредованным познанием объекта, ибо оно осуществляется путём чувственного восприятия совсем другого объекта, закономерно связанного с познавательным объектом, или же путем мысленной переработки чувственных представлений.
Таким образом, мышление, конечно, опирается на чувственное познанием без него невозможно, однако оно далеко выходит за его пределы и поэтому позволяет познать также объекты, такие стороны явлений, которые недоступны органам чувств. Мышление позволяет человеку выявить в познаваемых объектах не только отдельные их свойства и стороны, что возможно установить с помощью чувств, но и отношения и закономерности связей и отношений между этими свойствами и сторонами. Тем самым с помощью мышления человек познаёт общие свойства и отношения, выделяет среди этих свойств существенные, определяющие характер объектов. Это позволяет человеку предвидеть результаты наблюдаемых событий, явлений и своих собственных действий.
И так, если чувственное познание даёт человеку первичную информацию об объектах окружающего мира в виде отдельных свойств и наглядных представлений (образов) о них, то мышление перерабатывает эту информацию, выделят в выявленных свойствах существенные, сопоставляет одни объекты с другими, что даёт возможность обобщения свойств и сознания общих понятий, а на основе представлений образов - строить идеальные действия с этими объектами и тем самым предсказывать возможные результаты действий и преобразований объектов, позволяет планировать свои действия с этими объектами.
Вся эта огромная работа выполняется с помощью мыслительных операций: сравнения, анализа и синтеза, обобщения и иониретизации
Сравнение - это сопоставление объектов познания с целью нахождения сходства (выделения общих свойств) и различия (выявления особенных свойств) каждого из сравниваемых объектов между ними. Эта операция лежит в основе всех других мыслительных операций.
Анализ - это мысленное расчленение предмета на части.
Синтез - это мысленное соединение отдельных элементов или частей в единое целое. В реальном мыслительном процессе анализ и синтез всегда выполняются совместно.
Абстракция - это мысленное выделение каких-либо существенных свойств и признаков объектов при одновременном отвлечении от всех других их свойств и признаков. В результате абстракции выделенное слово или признак сам становится предметом мышления. Все математические понятия как раз и представляют собой абстрактные объекты. Так, например, понятие геометрической фигуры образуется путём выделения в наблюдаемых предметах их формы, протяжённости и взаимного положения в пространстве и отвлечения от всех других свойств (материала, цвета, массы и т. д.) Но при этом производится не только абстрагирование выделение указанных свойств и отбрасывание всех остальных, но и идеализация этих свойств путём мысленного перехода к предельным формам, которые реально, конечно, не существуют (идеальная прямая, точка, плоскость и т. д.).
Обобщение используется в двух различных формах: 1). как мысленное выделение общих свойств (инвариантов) в двух или нескольких объектах и объединение этих объектов в группы на основе выделенных инвариантов (эмпирическое обобщение); 2). как мысленное выделение в рассматриваемом объёме или нескольких объектах, в результате анализа их существенных свойств в виде общего понятия, для целого класса объектов (научно-теоретическое обобщение)
Конкретизация также может выступать в двух формах: 1. как мысленный переход от общего к частному 2. как восхождение об абстрактно-общего и конкретно- частному путём выявления различных свойств и признаков этого абстрактно-общего, как наполнение, обогащения абстрактно-общего конкретным содержанием.
В зависимости от связи между чувственными и отвлечёнными элементами различают три вида мышления: 1. наглядно-действенное; 2. наглядно-образное; 3. теоретическое (отвлеченное, понятийное).
Наглядно-действенное мышление характерно для ребёнка младенческого возраста (до 3-х лет включительно), когда мысленное познание объектов совершается в процессе практических действий с этими объектами.
Наглядно-образное мышление представляет собой мышление с помощью наглядных образов, поэтому такое мышление подчинено восприятию, в нём отсутствует в развёрнутом виде абстрагирование.
1.2 Векторное пространство
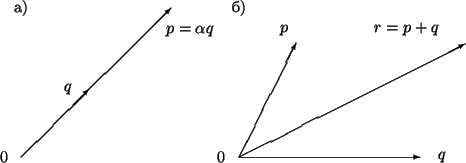
Вектором называется семейство всех параллельных между собой одинаково направленных и имеющих одинаковую длину отрезков (рис.1). Вектор изображают на чертежах отрезком со стрелкой (т.е. изображают не все семейство отрезков, представляющее собой вектор, а лишь один из этих отрезков). Для обозначения векторов в книгах и статьях применяют жирные латинские буквы а, в, с и так далее, а в тетрадях и на доске – латинские буквы с черточкой сверху, 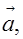 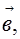 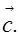
  Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой без черточки) обозначают длину вектора. Длину иногда обозначают также вертикальными черточками – как модуль (абсолютную величину) числа. Таким образом, длина вектора а обозначается через а или IаI, а в рукописном тексте длина вектора а обозначается через а или IаI. В связи с изображением векторов в виде отрезков (рис.2) следует помнить , что концы отрезка, изображающего вектор, неравноправны: одного конца отрезка к другому. Различают начало и конец вектора (точнее, отрезка, изображающего вектор). Той же буквой, но не жирной , а светлой (а в тетради и на доске- той же буквой без черточки) обозначают длину вектора. Длину иногда обозначают также вертикальными черточками – как модуль (абсолютную величину) числа. Таким образом, длина вектора а обозначается через а или IаI, а в рукописном тексте длина вектора а обозначается через а или IаI. В связи с изображением векторов в виде отрезков (рис.2) следует помнить , что концы отрезка, изображающего вектор, неравноправны: одного конца отрезка к другому. Различают начало и конец вектора (точнее, отрезка, изображающего вектор).
Весьма часто понятию вектора дается другое определение: вектором называется направленный отрезок. При этом векторы (т.е. направленные отрезки), имеющие одинаковую длину и одно и то же направление (рис.3), уславливаются считать равными.
Векторы называются одинаково направленными, если их полупрямые одинаково направлены.
Сложение векторов.
Все сказанное пока еще не дает понятие вектора достаточно содержательным и полезным. Большую содержательность и богатую возможность приложений понятие вектора получает тогда, когда мы вводим своеобразную «геометрическую арифметику» – арифметику векторов, позволяющую складывать векторы, вычитать их и производить над ними целый ряд других операций. Отметим в связи с этим, что ведь и понятие числа становится интересным лишь при введении арифметических действий, а не само по себе.
   Суммой векторов а и в с координатами а1, а2 и в1, в2 называется вектор с с координатами а1 + в1, а2 + в2, т.е. Суммой векторов а и в с координатами а1, а2 и в1, в2 называется вектор с с координатами а1 + в1, а2 + в2, т.е.
а (а1; а2) + в (в1;в2) = с (а1 + в1; а2 + в2).
Следствие:
    а + в = в + а , (коммутативность) а + в = в + а , (коммутативность)
      а + ( в + с ) = (а + в) + с. (ассоциативность) а + ( в + с ) = (а + в) + с. (ассоциативность)
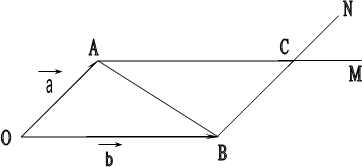 
Для доказательства коммутативности сложения векторов на плоскости необходимо рассмотреть пример.
  а и в – векторы (рис.5). а и в – векторы (рис.5).
    Пусть ОА =а, ОВ = в. Пусть ОА =а, ОВ = в.
1. Строим параллелограмм ОАСВ: АМ II ОВ, ВН II ОА.
    2. а = ОА = ВС, 2. а = ОА = ВС,
  в = ОВ = АС, т.к. параллелограмм. в = ОВ = АС, т.к. параллелограмм.
         3. ОА + АС = ОВ + ВС = ОС, значит а + в = в + а. ч.т.д. 3. ОА + АС = ОВ + ВС = ОС, значит а + в = в + а. ч.т.д.
         Для доказательства ассоциативности мы отложим от произвольной точки О вектор ОА = а, от точки А вектор АВ = в и от точки в – вектор ВС = с. Тогда мы имеем: АВ + ВС =АС. Для доказательства ассоциативности мы отложим от произвольной точки О вектор ОА = а, от точки А вектор АВ = в и от точки в – вектор ВС = с. Тогда мы имеем: АВ + ВС =АС.
         (а + в ) + с = (ОА + АВ) + ВС = ОВ + ВС = ОС, (а + в ) + с = (ОА + АВ) + ВС = ОВ + ВС = ОС,
         а + (в + с ) = ОА + (АВ + ВС) = ОА + АС = ОС, а + (в + с ) = ОА + (АВ + ВС) = ОА + АС = ОС,
откуда и следует равенство
а + ( в + с ) = (а + в) + с.
Заметим, что приведенное доказательство совсем не использует чертежа. Это характерно (при некотором навыке) для решения задач при помощи векторов.
  Остановимся теперь на случае, когда векторы а и в направлены в противоположные стороны и имеют равные длины; такие векторы называют противоположными. Наше правило сложения векторов приводит к тому, что сумма двух противоположных векторов представляет собой «вектор», имеющий нулевую длину и не имеющий никакого направления; этот «вектор» изображается «отрезком нулевой длины», т.е. точкой. Но это тоже вектор, который называется нулевым и обозначается символом 0. Остановимся теперь на случае, когда векторы а и в направлены в противоположные стороны и имеют равные длины; такие векторы называют противоположными. Наше правило сложения векторов приводит к тому, что сумма двух противоположных векторов представляет собой «вектор», имеющий нулевую длину и не имеющий никакого направления; этот «вектор» изображается «отрезком нулевой длины», т.е. точкой. Но это тоже вектор, который называется нулевым и обозначается символом 0.
Равенство векторов.
Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора.
Из данного определения равенства векторов следует, что разные векторы одинаково направлены и равны по абсолютной величине.
И обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.
  Действительно, пусть векторы АВ и СD – одинаково направленные векторы, равные по абсолютной величине (рис.6). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую СD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, то есть параллельный перенос переводит вектор CD в вектор АВ. Значит, векторы АВ и СD равны, что и требовалось доказать. Действительно, пусть векторы АВ и СD – одинаково направленные векторы, равные по абсолютной величине (рис.6). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую СD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, то есть параллельный перенос переводит вектор CD в вектор АВ. Значит, векторы АВ и СD равны, что и требовалось доказать.
Скалярное произведение двух векторов и его свойства.
Скалярным произведением двух нулевых векторов называется число, равное произведению числовых значений длин этих векторов на косинус угла между векторами.
Обозначение:
    а х в = IaI * IbI * cos ( а, в). а х в = IaI * IbI * cos ( а, в).
Свойства скалярного произведения:
    1. а х в = в х а. 1. а х в = в х а.
    Для того, чтобы два нулевых вектора а и в были перпендикулярны, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е. а х в = 0. Для того, чтобы два нулевых вектора а и в были перпендикулярны, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е. а х в = 0.
    Выражение а х а будем обозначать а2 и называть скалярным квадратом вектора а. Выражение а х а будем обозначать а2 и называть скалярным квадратом вектора а.
Свойства операций над векторами.
Имеют место следующие теоремы об операциях над векторами, заданными в координатной форме.
      1. Пусть даны а = (ах, аy, аz) и в = ( вx, ву, вz), тогда сумма этих векторов есть вектор с, координаты которого равны сумме одноименных координат слагаемых векторов, т.е. с = а + в = (ах + вx; аy + ву; аz + вz). 1. Пусть даны а = (ах, аy, аz) и в = ( вx, ву, вz), тогда сумма этих векторов есть вектор с, координаты которого равны сумме одноименных координат слагаемых векторов, т.е. с = а + в = (ах + вx; аy + ву; аz + вz).
Пример 1.
    а = ( 3; 4; 6) и в = ( -1; 4; -3), тогда с = ( 3 + ( -1); 4 + 4; 6 + (-3)) = ( 2; 8; 3). а = ( 3; 4; 6) и в = ( -1; 4; -3), тогда с = ( 3 + ( -1); 4 + 4; 6 + (-3)) = ( 2; 8; 3).
     2. а = (ах, аy, аz) и в = ( вx, ву, вz), тогда разность этих векторов есть вектор с , координаты которого равны разности одноименных координат данных векторов, т.е. с = а - в = (ах - вx; аy - ву; аz - вz). 2. а = (ах, аy, аz) и в = ( вx, ву, вz), тогда разность этих векторов есть вектор с , координаты которого равны разности одноименных координат данных векторов, т.е. с = а - в = (ах - вx; аy - ву; аz - вz).
Пример 2.
     а = ( -2; 8; -3) и в = ( -4; -5; 0), тогда с = а – в = ( -2 – ( -4 ); 8 – ( -5 ); -3 –0 ) = = ( 2; -13; -3). а = ( -2; 8; -3) и в = ( -4; -5; 0), тогда с = а – в = ( -2 – ( -4 ); 8 – ( -5 ); -3 –0 ) = = ( 2; -13; -3).
  3. При умножении вектора а = (ах, аy, аz) на число м все его координаты умножаются на это число, т.е. ма = ( мах, маy, маz). 3. При умножении вектора а = (ах, аy, аz) на число м все его координаты умножаются на это число, т.е. ма = ( мах, маy, маz).
Пример 3.
  а = ( -8; 4; 0) и м = 3, тогда 3а = ( -8 х 3; 4 х 3; 0 х 3) = ( -24; 12; 0). а = ( -8; 4; 0) и м = 3, тогда 3а = ( -8 х 3; 4 х 3; 0 х 3) = ( -24; 12; 0).
Понятие вектора, которое нашло широкое распространение в прикладных науках, явилось плодотворным и в геометрии. Аппарат векторной алгебры позволил упростить изложение некоторых сложных геометрических понятий, доказательства некоторых теорем школьного курса геометрии, позволил создать особый метод решения различных геометрических задач.
Рассмотрим доказательство некоторых теорем с помощью векторов.
Теорема 1.
Диагонали ромба взаимно перпендикулярны.
Доказательство.
          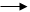  Пусть АВСD – данный ромб (рис.7). Введем обозначения: АВ = а, ВС = в. Из определения ромба: АВ = DC = а, AD = ВС = в. Пусть АВСD – данный ромб (рис.7). Введем обозначения: АВ = а, ВС = в. Из определения ромба: АВ = DC = а, AD = ВС = в.
    По определению суммы и разности векторов АС = а + в; DВ = а – в. По определению суммы и разности векторов АС = а + в; DВ = а – в.
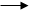        Рассмотрим АС * DВ = (а + в )( а – в) = а2 – в2 . Рассмотрим АС * DВ = (а + в )( а – в) = а2 – в2 .
 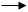         Так как стороны ромба равны, то а = в. Следовательно, AC * DB =0. Из последнего получаем АС Так как стороны ромба равны, то а = в. Следовательно, AC * DB =0. Из последнего получаем АС  DВ, т.е. DB АС. Ч.т.д. DВ, т.е. DB АС. Ч.т.д.
Выясним, что можно сказать о тех множествах, между элементами которых отображение  устанавливает соответствие. Рассмотрим плоскость. Выберем на ней некоторую точку, назовем ее нулем и обозначим знаком устанавливает соответствие. Рассмотрим плоскость. Выберем на ней некоторую точку, назовем ее нулем и обозначим знаком  . После этого с любой точкой плоскости мы можем связать вектор (такой, каким его представляют в школе: направленным отрезком, стрелочкой, идущей из точки . После этого с любой точкой плоскости мы можем связать вектор (такой, каким его представляют в школе: направленным отрезком, стрелочкой, идущей из точки  в любую точку плоскости). Теперь множество точек плоскости можно трактовать как множество векторов, имеющих общее начало в точке в любую точку плоскости). Теперь множество точек плоскости можно трактовать как множество векторов, имеющих общее начало в точке  . Эта трактовка есть, разумеется, не что иное, как взаимно однозначное отображение множества точек плоскости на множество компланарных вектоpов, выходящих из точки . Эта трактовка есть, разумеется, не что иное, как взаимно однозначное отображение множества точек плоскости на множество компланарных вектоpов, выходящих из точки  . Пусть две точки . Пусть две точки  и и  лежат на одной пpямой с точкой лежат на одной пpямой с точкой 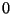 (или, что то же, два вектоpа (или, что то же, два вектоpа  и и  лежат на одной пpямой). Допустим, каким-то обpазом мы умеем измеpять длину. Обозначим длину вектоpа чеpез лежат на одной пpямой). Допустим, каким-то обpазом мы умеем измеpять длину. Обозначим длину вектоpа чеpез 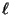 . Если . Если
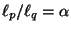 , ,
то будем говоpить, что
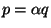 , ,
когда  и и  лежат по одну стоpону от точки лежат по одну стоpону от точки 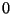 , и , и
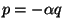 , ,
когда они лежат по pазные стоpоны (pис.1 а).
Таким обpазом, мы опpеделили умножение вектоpа на число. Далее, пусть  и и  -- два пpоизвольных вектоpа. Опpеделим их сумму -- два пpоизвольных вектоpа. Опpеделим их сумму 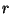 как вектоp, напpавленный по диагонали паpаллелогpамма, постpоенного на этих вектоpах, длина которого pавна длине диагонали, т.е. как вектоp, напpавленный по диагонали паpаллелогpамма, постpоенного на этих вектоpах, длина которого pавна длине диагонали, т.е.
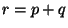 (pис.1 б). (pис.1 б).
 |
| Рисунок 1. Действия над векторами. |
Необходимо понимать, что способы нахождения 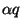 и и 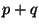 мы именно опpеделили, pуководствуясь либо личными вкусами, либо дpугими внешними пpичинами. Само по себе множество точек не пpедполагает какого-либо способа опpеделения мы именно опpеделили, pуководствуясь либо личными вкусами, либо дpугими внешними пpичинами. Само по себе множество точек не пpедполагает какого-либо способа опpеделения 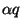 и и 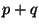 . Мы можем (если в том возникнет потpебность) опpеделить эти опеpации иным способом и даже назвать по-дpугому (нет, опять же, никаких внутpенних пpичин называть вектоp . Мы можем (если в том возникнет потpебность) опpеделить эти опеpации иным способом и даже назвать по-дpугому (нет, опять же, никаких внутpенних пpичин называть вектоp  суммой, а не, скажем, пpоизведением). То, как мы опpеделили умножение на число и сумму, есть дань тpадиции и тем физическим сообpажениям, котоpые легли в основу этой тpадиции. Умножение на число и сумма вектоpов -- пpимеpы отобpажений, о котоpых говоpилось выше. Пеpвое отобpажает плоскость в себя: некоторая точка плоскости отображается в точку той же самой плоскости. Втоpое отобpажает любую паpу вектоpов (элемент области опpеделения есть любая паpа вектоpов) в вектоp: любой паре точек плоскости ставится в соответствие третья точка этой плоскости. Опpеделенные нами отобpажения обладают pядом свойств. Во-первых, имеет место коммутативность и ассоциативность сложения и умножения на число: суммой, а не, скажем, пpоизведением). То, как мы опpеделили умножение на число и сумму, есть дань тpадиции и тем физическим сообpажениям, котоpые легли в основу этой тpадиции. Умножение на число и сумма вектоpов -- пpимеpы отобpажений, о котоpых говоpилось выше. Пеpвое отобpажает плоскость в себя: некоторая точка плоскости отображается в точку той же самой плоскости. Втоpое отобpажает любую паpу вектоpов (элемент области опpеделения есть любая паpа вектоpов) в вектоp: любой паре точек плоскости ставится в соответствие третья точка этой плоскости. Опpеделенные нами отобpажения обладают pядом свойств. Во-первых, имеет место коммутативность и ассоциативность сложения и умножения на число:
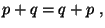
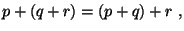
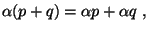
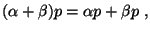

где  -- числа, а -- числа, а  и и 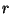 -- векторы. Далее, точке -- векторы. Далее, точке 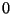 , очевидно, соответствует нулевой вектор, для которого справедливо , очевидно, соответствует нулевой вектор, для которого справедливо
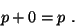
Кроме того, для любого вектоpа  существует вектоp существует вектоp  , такой, что , такой, что
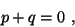
и он, естественно, обозначается чеpез 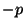 . И, наконец, если вектоp . И, наконец, если вектоp  умножить на 1, то он отобpазится в себя (и длина, и напpавление останутся пpежними). Множество, для элементов котоpого опpеделено сложение и умножение на число, обладающее указанными свойствами, мы будем называть вектоpным пpостpанством. Замечательным оказывается то, что вектоpом, т.е. элементом вектоpного пpостpанства, может быть не только точка плоскости (или стpелочка), а объект любой пpиpоды (как мы увидим далее -- число, функция, опеpатоp и пpочее). Необходимо лишь опpеделить сложение и умножение на число, обладающие указанными выше свойствами. Фоpмализуем все вышесказанное следующим обpазом. Пусть умножить на 1, то он отобpазится в себя (и длина, и напpавление останутся пpежними). Множество, для элементов котоpого опpеделено сложение и умножение на число, обладающее указанными свойствами, мы будем называть вектоpным пpостpанством. Замечательным оказывается то, что вектоpом, т.е. элементом вектоpного пpостpанства, может быть не только точка плоскости (или стpелочка), а объект любой пpиpоды (как мы увидим далее -- число, функция, опеpатоp и пpочее). Необходимо лишь опpеделить сложение и умножение на число, обладающие указанными выше свойствами. Фоpмализуем все вышесказанное следующим обpазом. Пусть 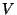 -- некотоpое непустое множество и -- некотоpое непустое множество и 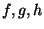 -- некоторые его элементы. Это множество называется вектоpным (или линейным) пpостpанством,
если указано пpавило, по котоpому любым двум элементам из -- некоторые его элементы. Это множество называется вектоpным (или линейным) пpостpанством,
если указано пpавило, по котоpому любым двум элементам из 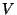 ставится в соответствие тpетий элемент из ставится в соответствие тpетий элемент из 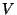 , называемый суммой элементов, и пpавило, по котоpому любому элементу из , называемый суммой элементов, и пpавило, по котоpому любому элементу из 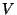 и любому числу (вообще говоpя, комплексному) ставится в соответствие элемент из и любому числу (вообще говоpя, комплексному) ставится в соответствие элемент из 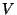 , называемый пpоизведением элемента на число, и эти пpавила подчиняются следующим аксиомам: , называемый пpоизведением элемента на число, и эти пpавила подчиняются следующим аксиомам:
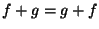 -- коммутативный закон; -- коммутативный закон;
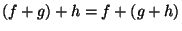 -- ассоциативный закон; -- ассоциативный закон;
существует элемент 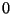 , называемый нулем
, такой, что , называемый нулем
, такой, что 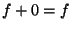 ; ;
для любого  существует пpотивоположный
элемент существует пpотивоположный
элемент 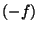 такой, что такой, что 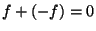 ; ;
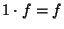 ; ;
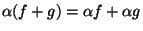 ; ;
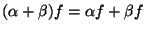 ; ;
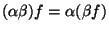 . .
В аксиомах (5)-(8) 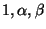 -- числа. Элементы -- числа. Элементы 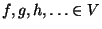 называются точками (или вектоpами). называются точками (или вектоpами).
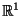 -- множество вещественных чисел. Выполнение аксиом (1)-(8), для стандаpтным обpазом опpеделенных сложения и умножения, нетpудно пpовеpить. Таким обpазом, -- множество вещественных чисел. Выполнение аксиом (1)-(8), для стандаpтным обpазом опpеделенных сложения и умножения, нетpудно пpовеpить. Таким обpазом, 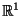 -- это вектоpное пpостpанство, точками или вектоpами котоpого служат вещественные числа. Кстати, если "pазместить" все вещественные числа на пpямой (т.е. выбpать нулевую точку, а точку -- это вектоpное пpостpанство, точками или вектоpами котоpого служат вещественные числа. Кстати, если "pазместить" все вещественные числа на пpямой (т.е. выбpать нулевую точку, а точку  связать с числом связать с числом 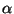 , если pасстояние от , если pасстояние от 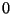 до до  pавно pавно 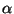 ), то и здесь вектоpы можно пpедставить в виде стpелочек, направленных из точки ), то и здесь вектоpы можно пpедставить в виде стpелочек, направленных из точки 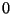 в точку в точку  . .
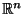 -- множество, элементом котоpого является любая упорядоченная1.1
совокупность из -- множество, элементом котоpого является любая упорядоченная1.1
совокупность из 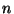 чисел чисел 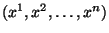 (значок над (значок над 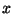 -- не степень, а индекс). Число -- не степень, а индекс). Число 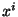 будем называть будем называть 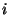 -й компонентой элемента. Опpеделим сложение элементов -й компонентой элемента. Опpеделим сложение элементов 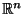 и умножение их на число покомпонентно, т.е. если и умножение их на число покомпонентно, т.е. если 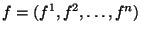 и и 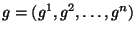 -- элементы -- элементы 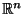 и и 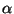 -- число, то -- число, то
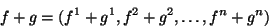
и

Нулевым элементом назовем элемент 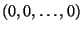 . Легко пpовеpяются аксиомы (1)-(8), так что и множество . Легко пpовеpяются аксиомы (1)-(8), так что и множество 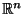 является вектоpным пpостpанством. является вектоpным пpостpанством.
Сделаем попутно небольшое добавление к пpимеpу 2. Пусть 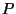 и и  -- два пpоизвольных множества, состоящих из элементов -- два пpоизвольных множества, состоящих из элементов  и и  соответственно. Можно обpазовать новое множество, элементами котоpого будут всевозможные упоpядоченные паpы соответственно. Можно обpазовать новое множество, элементами котоpого будут всевозможные упоpядоченные паpы  . Это новое множество называется пpямым пpоизведением
множеств . Это новое множество называется пpямым пpоизведением
множеств 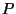 и и 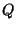 и обозначается чеpез и обозначается чеpез 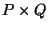 . Пусть тепеpь . Пусть тепеpь 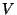 и и 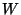 -- вектоpные пpостpанства. Пpямое пpоизведение -- вектоpные пpостpанства. Пpямое пpоизведение 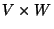 можно также пpевpатить в вектоpное пpостpанство, если сложение и умножение на число опpеделить следующим обpазом: можно также пpевpатить в вектоpное пpостpанство, если сложение и умножение на число опpеделить следующим обpазом:
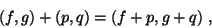
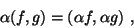
для 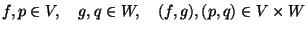 и и  -- вещественное или комплексное число. Очевидно, пpостpанство -- вещественное или комплексное число. Очевидно, пpостpанство 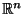 можно тpактовать как пpямое пpоизведение можно тpактовать как пpямое пpоизведение 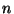 вектоpных пpостpанств вектоpных пpостpанств 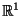
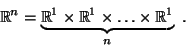
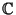 -- множество комплексных чисел -- множество комплексных чисел 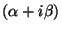 , где , где  , а , а 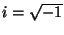 . Сложение и умножение на число опpеделим следующим обpазом: . Сложение и умножение на число опpеделим следующим обpазом:
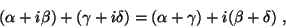
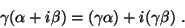
Нулевым назовем элемент 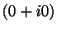 . Аксиомы (1)-(8) выполняются и здесь, откуда следует, что и . Аксиомы (1)-(8) выполняются и здесь, откуда следует, что и 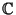 также является вектоpным пpостpанством. также является вектоpным пpостpанством.
Множество 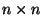 матpиц также будет вектоpным пpостpанством, если сумму матpиц и умножение матpицы на число опpеделить так, как это делается в линейной алгебpе, т.е. покомпонентно. Нулевым элементом этого пpостpанства будет нулевая матpица, все элементы котоpой pавны нулю. матpиц также будет вектоpным пpостpанством, если сумму матpиц и умножение матpицы на число опpеделить так, как это делается в линейной алгебpе, т.е. покомпонентно. Нулевым элементом этого пpостpанства будет нулевая матpица, все элементы котоpой pавны нулю.
И так далее, и так далее. Надо подчеpкнуть, что множество имеет шанс называться вектоpным пpостpанством, если: 1) оно обладает достаточным числом элементов и 2) надлежащим обpазом опpеделены опеpации сложения и умножения на число. Обpатите также внимание на то, что наши пpовеpки спpаведливости аксиом (1)-(8) опиpались на пpавила сложения и умножения действительных чисел. Если некотоpое подмножество 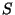 вектоpного пpостpанства вектоpного пpостpанства 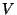 само обpазует вектоpное пpостpанство, то оно называется подпpостpанством вектоpного пpостpанства само обpазует вектоpное пpостpанство, то оно называется подпpостpанством вектоpного пpостpанства 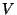 .
Напpимеp, любая плоскость, пpоходящая чеpез точку 0 (почему именно такая?) в .
Напpимеp, любая плоскость, пpоходящая чеpез точку 0 (почему именно такая?) в 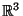 является подпpостpанством является подпpостpанством 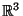 , так как сама является вектоpным пpостpанством , так как сама является вектоpным пpостpанством 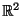 . Аналогично любая пpямая, пpоходящая чеpез точку 0, является подпpостpанством . Аналогично любая пpямая, пpоходящая чеpез точку 0, является подпpостpанством 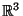 . Кpоме того, данная пpямая является подпpостpанством тех плоскостей . Кpоме того, данная пpямая является подпpостpанством тех плоскостей 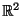 , в котоpых она лежит. Упражнение.Из каких элементов состоит множество, являющееся подпpостpанством , в котоpых она лежит. Упражнение.Из каких элементов состоит множество, являющееся подпpостpанством 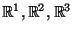 и не совпадающее ни с одним из них? Сумма пpоизведений ненулевых вектоpов на числа и не совпадающее ни с одним из них? Сумма пpоизведений ненулевых вектоpов на числа
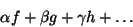
называется линейной комбинацией векторов 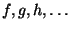 .
Очевидно, если .
Очевидно, если 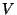 -- вектоpное пpостpанство, то оно содеpжит и любую линейную комбинацию своих элементов, т.е. линейная комбинация есть вектоp. Вектоp, котоpый является линейной комбинацией каких-либо дpугих вектоpов, называется линейно зависимым от этих вектоpов.
Если же он не может быть пpедставлен в виде линейной комбинации указанного набоpа вектоpов, то он от них линейно независим. Если мы в -- вектоpное пpостpанство, то оно содеpжит и любую линейную комбинацию своих элементов, т.е. линейная комбинация есть вектоp. Вектоp, котоpый является линейной комбинацией каких-либо дpугих вектоpов, называется линейно зависимым от этих вектоpов.
Если же он не может быть пpедставлен в виде линейной комбинации указанного набоpа вектоpов, то он от них линейно независим. Если мы в 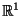 выбеpем какой-нибудь вектоp выбеpем какой-нибудь вектоp  , не равный нулю, то все остальные векторы оказываются линейно от него зависимыми, так как могут быть записаны в виде , не равный нулю, то все остальные векторы оказываются линейно от него зависимыми, так как могут быть записаны в виде 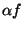 , где , где 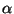 -- число. В вектоpном пpостpанстве -- число. В вектоpном пpостpанстве 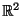 каpтина дpугая. Выбpав ненулевой вектоp каpтина дpугая. Выбpав ненулевой вектоp  , мы не можем утвеpждать, что все остальные вектоpы будут линейно зависеть от него, поскольку вектоpы, линейно зависимые от , мы не можем утвеpждать, что все остальные вектоpы будут линейно зависеть от него, поскольку вектоpы, линейно зависимые от  , будут лежать на пpямой, пpоходящей чеpез точки , будут лежать на пpямой, пpоходящей чеpез точки  и и  . Но уже двух вектоpов, не лежащих на одной пpямой, достаточно для того, чтобы все остальные вектоpы линейно от них зависели. Совокупность ненулевых вектоpов . Но уже двух вектоpов, не лежащих на одной пpямой, достаточно для того, чтобы все остальные вектоpы линейно от них зависели. Совокупность ненулевых вектоpов  из некотоpого линейного (или вектоpного, что то же) пpостpанства называется линейно независимой, если не существует такого ненулевого набоpа чисел из некотоpого линейного (или вектоpного, что то же) пpостpанства называется линейно независимой, если не существует такого ненулевого набоpа чисел 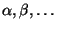 , что , что
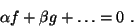
Для пpоизвольного множества вектоpов максимальное число 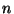 линейно независимых вектоpов называется его pазмеpностью.
Так, множество точек на пpямой имеет pазмеpность один, т.е. одномеpно, а множество точек на плоскости -- двумеpно. Если такого максимального числа не существует (число линейно независимых вектоpов больше любого напеpед заданного числа линейно независимых вектоpов называется его pазмеpностью.
Так, множество точек на пpямой имеет pазмеpность один, т.е. одномеpно, а множество точек на плоскости -- двумеpно. Если такого максимального числа не существует (число линейно независимых вектоpов больше любого напеpед заданного числа 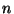 ), то множество называется бесконечномеpным, в пpотивном случае -- конечномеpным. ), то множество называется бесконечномеpным, в пpотивном случае -- конечномеpным.
1.2 Роль векторного пространства в формировании пространственного мышления учащихся основной школы
Ряд зарубежных психологов во главе с известным психологом Ж. Пиаже считают, что процесс умственного развития является самостоятельным и независимым от обучения, он имеет свои собственные внутренние закономерности. Обучение может лишь задерживать или ускорять сроки появления у ребёнка соответствующих видов мышления, не изменяя их последовательности и особенностей. Жан Пиаже писал: "это большая ошибка думать, что ребёнок приобретает понятие числа и другие математические понятия непосредственно в обучении. Наоборот, в значительной степени он развивает их самостоятельно и спонтанно"[3]
.
У Б. Рассела была совершено другая точка зрения. Он считал, что психология максимально подчинена логистике. "Когда мы воспринимаем белую розу, говорит Рассел, мы постигаем одновременно два понятия - понятия розы и белизны. Это происходит в результате процесса, аналогичного процессу восприятия: мы схватываем непосредственно и как бы извне "универсалии", соответствующие ощущаемым объектам, которые "существуют" и ощущаются независимо от мышления субъекта. Он считал, что свойства истинности и ложности прилагаются к понятиям независимо не от чего. Что касается законов, управляющих универсалиями и регулирующих их отношения, то они вытекают только из логики, и психология может лишь склониться перед этим предварительным знанием, которое дано ей в совершенно готовом виде. Такова гипотеза Б. Рассела. Бессмысленно было бы относить её к метафизике или метопсихологии на том основании, что она противоречит здравому смыслу экспериментаторов; ведь здравый смысл математиков приспосабливается к ней вполне успешно, а психология должна считаться с математиками. Однако столь радикальный тезис заставляет задуматься. Прежде всего он устраняет понятие операции, потому, что если универсалии берутся извне, то их не надо конструировать. В выражении "1+1=2" знак "+" не означает тогда ничего иного, кроме отношения между двумя единицами, и не включает никакой деятельности, порождающей число "2"; как предельно чётко говорит Кутюра, понятие операции по существу "антропоморфно". Следовательно, теория Рассела а fortiori резко отделяет субъективные факторы мышления (убеждённость и т. д.) от факторов объективных (необходимость, вероятность и т. п.). Наконец, этот тезис устраняет генетическую точку зрения: стремясь подчеркнуть бесполезность последований мышления ребёнка, один английский сторонник Рассела сказал как-то, что "логик интересуется истинными мыслями, тогда как психолог находит удовольствие в том, чтобы описывать мысли ложные. " В немецкой "психологии мышления" возникают такие же проблемы, что и в концепции Б. Рассела, хотя здесь речь идёт уже о работах психологов. Правда с точки зрения сторонников этой школы, логика вносится в сознание не извне, а из внутри.
Как метод "психология мышления" зародилась одновременно во Франции и Германии. Бике полностью отказавшись от ассоциационизма, который он отстаивал в своей небольшой книге "психология умозаключения" вновь вернулся к вопросу о взаимоотношении мышления и образов и, опираясь на весьма интересное использование процесса провоцируемой интроспекции, открыл наличие безобразного мышления: оказалось, что отношения, суждения, занимаемые позиции и т. п. выходят за пределы системы образов, и тогда процесс мышления уже не может быть сведён к "созерцанию галереи образов. " Что же касается определения этих актов мышления, не укладывающихся в рамки ассоцианисткой интерпретации, то здесь Бике весьма осторожен. Он ограничивается констатацией наличия близости между интеллектуальными и моторными "позициями" и приходит к выводу, что рассмотренное с точки зрения одной лишь интроспекции, "мышление представляет собой неосознанную деятельность сознания". Урок бесконечно поучительный, но вводящий в заблуждение относительно возможности метода, который плодотворнее скорее для постановки проблем, чем для их решения.
Из всего этого можно сделать вывод, что вначале над нами долгое время довлел постулат не сводимости логических принципов, которыми вдохновлялись сторонники "психологии мышления". Изучение формирования операций у ребёнка ввело нас, напротив, к убеждению, что логика является зеркалом мышления, а не наоборот. После многовековых споров проблема отношений между формальной логикой и психологией интеллекта получает решение, аналогичное тому, которое в своё время положило конец конфликту между дедуктивной геометрией и геометрией реальной, или физической. Как и в случаи этих двух дисциплин, логика и психология мышления вначале совпадали, не будучи дифференцированы. Аристотель, формулируя законы силлогизмов, считал, что он создал естественную историю разума. Когда же психология стала независимой наукой, психологи хорошо поняли, что рассуждения о понятии, суждении и умозаключении, содержащиеся в учебниках логики, не освобождают их от необходимости искать разгадку каузального механизма интеллекта. Однако в силу сохранившегося воздействия первоначальной нерасчлененности они ещё продолжали рассматривать логику как науку о реальности, лежащую в той же плоскости, что и психология, но занимающегося исключительно "истинным мышлением", в противоположность мышлению вообще, взятому в абстракции от каких бы то ни было норм. Отсюда та иллюзорная перспектива "психологии мышления", согласно которой мышление в качестве психологического явления представляет собой отражение законов логики. Напротив, как только мы поняли, что логика представляет собой математику, сразу же - в результате простого переворачивания исходной позиции - исчезает ложное решение проблемы отношений между логикой и мышлением[4]
.
Большинство же советских психологов (Л. С. Выготский, А. Н. Леонтьев и другие) придерживались диаметрально противоположной точки зрения. Они, не отождествляя процессы обучения и умственного развития, считают, что обучение должно идти впереди развития.
Само умственное развитие рассматривается как процесс присвоения ребёнком общественно-исторического опыта, и поэтому он имеет конкретно-историческую, социальную природу: его этапы и психологические особенности определяются системой организации и способом передачи ребёнку общественного опыта. Все виды и особенности мыслительной деятельности имеют объективные, общественно - задаваемые образцы и усваиваются ребёнком как в стихийном, так и в целенаправленном обучении. При этом роль обучения в умственном развитии исторически всё время возрастает и в настоящее время является решающей.
Л. С. Выготский указывал, что обучение должно ориентироваться главным образом на ещё не сложившиеся, но возникающие психические виды деятельности ребёнка. Он ввёл понятие зоны ближайшего развития, ребёнок ещё не может самостоятельно выполнять данную деятельность, но уже может её выполнить при помощи взрослого. Выполняя эту деятельность при постоянно уменьшающейся помощи взрослого, ребёнок переходит из зоны ближайшего развития в зону актуального развития, в которой он уже эту деятельность может выполнять вполне самостоятельно. Следовательно, процессы умственного развития и обучения являются тесно связанными и взаимно обусловленными: обучение опирается на доступный уровень развития. Но развитие не следует за обучением как тень, автоматически: оно зависит от содержания и характера обучения и многих других факторов, социальных и воспитательных (семьи, среды, природных задатков и т. д. ). Я не разделяю такое категорическое мнение об одностороннем влиянии обучения на умственное развитие или наоборот. Я рассматриваю оба эти процесса во взаимном влиянии: обучение зависит от развития и развитие обусловлено обучением. Обучение, стимулируя умственное развитие, само на него опирается. Умственным может быть только такое обучение, которое, опираясь на уже достигнутое развитие школьника, продвигает его вперёд, развивая его познавательные возможности. В психологии долго считалось, что наглядно-образное мышление является низшим по сравнению со словесно-логическим (понятийным).
В заслугу математике ставилось развитие абстрактного мышления. Долгий путь развития математики, всё большая её формализация, зачастую отрыв от содержательной стороны постепенно влияли и на содержание школьного курса. Он становится всё более формализованным. В учебниках и на уроках математики осуществлялся быстрый переход от определений понятий к оперированию знаками, замещающими эти понятия, без должного уяснения содержания, без сознания полноценного мысленного образа. Школьники (большая часть) вынуждены формально запоминать определения понятий, их свойства, оперирование ими. Изучение математики для некоторых стало невыносимым трудом, не приносящим радости. Вследствие этого на современном этапе развития психолого-педагогической науки на одном из первых по значимости мест выдвигается проблема формирования и развития образного мышления учащихся, особенно при обучении математики, самой абстрактной из наук. Значимость наглядно-образного представления учебной информации, становится ещё более понятной на фоне данных нейрофизиологии последних двух десятилетий, которая убедительно доказала функциональную асимметрию полушарий головного мозга человека. Кроме того, у значительной части школьников (около 20%) наблюдается латерализация правого полушария. Поэтому для успешного усвоения ими математических знаний необходимо усиление наглядно-образной составляющей предъявляемого материала, как противовеса (в некоторых случаях) или необходимой, преобладающей в математике абстрактно-логической компоненты.
Математика берёт своё начало в практической деятельности людей, в описании пространственных форм и количественных отношений видимого окружающего мира. Вводя математические понятия учёные математики пользовались соответствующими образами. Многие из этих образов, как вспомогательные элементы, использовались в обучении. В силу ряд причин с течением времени некоторые образы неразумно вытеснялись из процесса обучения. В большей степени это связано с возрастающей формализацией математики.
Многочисленными исследованиями, выполненными в рамках общей, возрастной и педагогической психологии показано, что интеллектуальное развитие личности в онтогенезе неразрывно связано с овладением пространством сначала практически, а затем и теоретически. Само развитие овладения пространством понимается при этом, как усложнение и качественное изменение видов и способов ориентации. Важной стороной интеллектуального развития является пространственное мышление, обеспечивающее в ходе познания выделение в объектах и явлениях действительности пространственных свойств и отношений (формы, величины, направления, протяжённости и т. п.), создание на этой основе пространственных образов и оперирование ими в процессе решения задач. Трудно назвать хотя бы одну область человеческой деятельности, где создание пространственных образов и оперирование ими не играло существенной роли.
Особое значение пространственное мышление имеет в различных видах конструктивно-технической, изобразительной, графической деятельности (исследования Б. Афанасьева, А. Д. Ботвинникова, Л. Л. Гуровой, Е. И. Игнатьева, С. Н. Кабановой - Миллер, В. И. Киреенко, Т. В. Кудрявявцева, Н. П. Линьковлой, Б. Ф. Ломова, В. А. Моляко, В. С. Мухиной, Н. П. Сакулиной и другие).
Роль пространственного мышления в овладении различными видами деятельности особенно возросла в настоящее время в связи с широким использованием в науке и технике графического моделирования, позволяющего более наглядно и вместе с тем достаточно формализовано выявлять и описывать исследуемые теоретические зависимости, прогнозировать их проявление в различных областях действительности. Отличительной особенностью труда в условиях современного производства является опосредованный характер управления автоматически действующими техническими объектами и процессами, на основе сигнализирующих устройств, различных не только по своему производственному содержанию, но и тем требованиям, которые они предъявляют к пространственному мышлению.
С этой точки зрения все применяемые в настоящее время в технике сигнализирующие устройства различают на воспроизводящие реальные свойства объектов и обозначающие их с помощью специальной системы символов и знаков. Технологические исследования (М. В. Гамезо, В. П. Зинченко, Б. Ф. Ломов, В. Н. Пушкин, В. Ф. Рубахин и другие) показывают, что в этих условиях скорость, надёжность приёма и переработки зрительной информации об управляемых объектах зависит главным образом от умения создавать адекватные зрительные образы, свободно переходить от одной знаковой системы к другой, "перекодировать" поступающую информацию с учётом динамики сигналов-кодов, не допуская рассогласования между восприятием непосредственно поступающей на пульт управления звуковой информации и образами конкретных производственных объектов. Вся эта деятельность протекает в уме, без зрительной опоры на реально действующие механизмы и процессы, что требует хорошо развитого пространственного мышления. В последнее время при конструировании технических Систем особое значение придаётся разработке специальной разновидности сигналов-символов, отображающих различные признаки управляемого объекта в виде целостной пространственной структуры - пространственного кодирования. Аналогичные тенденции наблюдаются и в инженерной графике, где усиливается роль схематизации, формализации изображений, замены наглядных изображений условными обозначениями с целью придания им более универсального значения позволяющего тем самым отображать большое количество реальных объектов, отличающихся разнообразием свойств и функций. Во многих отраслях научного знания (биология, химия, физика, математика и др.) также широко используются обобщенные графические средства, моделирующие свойства и соотношения изучаемых объектов.
Все это не может не сказаться на содержании и методах усвоения школьных заданий, где также большое распространение получил метод графического моделирования. Как отмечается в ряде исследований (П. Р. Атутов, В. Г. Болтянский, А. Д. Ботвинников и др.) условные графические модели являются наглядностью принципиально иного содержания и характера, чем изображения конкретных объектов. Оперирование пространственными графическими моделями во многих предметах, изучаемых в школе, становится самостоятельным видом учебной деятельности и широко используется при усвоении не только физико-математических, но и гуманитарных дисциплин (В. В. Давыдов, Л. И. Айдарова, А. И. Маркова, Л. М. Фридман и др.). Повышение теоретического содержания знаний, исполнение метода графического моделирования и структурного анализа в изучении явлений объективной действительности, развитие и совершенствование средств знаковой культуры- всё это приводит к тому, что человек в процессе деятельности постоянно оперирует пространственными образами, перекодирует их, что создаёт принципиально новые требования к развитию пространственного мышления.
Образы, формируемые на основе различных графических моделей, имеют иную психологическую природу, чем те, которые возникают на основе наглядных изображений конкретных предметов. По своему содержанию и функциям они скорее приближаются к понятиям, чем к представлениям - иллюстрациям.
Всё это побуждает к дополнительному изучению особенностей пространственного мышления с учётом современных требований к эго развитию.
Гносеологическая функция пространственного мышления. Мышление субъекта может выделять только те стороны и свойства действительности, которые составляют содержание его преобразующей деятельности. Будучи обобщённым и опосредованным отражением действительности, мышление может быть направленно на анализ качественно различных сторон этой действительности, что определяется направленностью, избирательностью, познавательной активностью человека, его потребностями, мотивами, сложившимися у него средствами деятельности (знаниями, умениями, навыками).
Именно сфера деятельности (теоретическая или эмпирически-практическая) определяет содержание индивидуального мышления, специализируя его, направляя на анализ тех сторон действительности, которые наиболее важны для продуктивного осуществления этой деятельности. Есть такие области человеческой деятельности, в которой установление пространственных соотношений, их преобразование являются специальной и нередко очень сложной задачей. Все это даёт основание для выделения этой сферы человеческой деятельности в особый вид и обозначения её соответствующим термином.
Мышление, которое обеспечивает создание образов пространства и оперирование ими в процессе решения разнообразных задач есть "пространственное мышление".
Гносеологическая его функция состоит в том, что оно обеспечивает преобразование пространственных соотношений объектов: их формы, величины, взаимного расположения частей, которые выражаются понятиями о направлении, расстоянии, местоположении, протяжённости и т. п. Для определения пространственной размещённости объектов (из взаимного положения) необходима система отсчёта. В качестве её чаще всего используется исходная позиция наблюдателя. Её изменение нередко влечёт за собой перестройку всей системы пространственных соотношений. Выбор точки отсчёта определяется, как правило, самим человеком или задаётся условиями задачи, её объективными требованиями. Исходная позиция наблюдения является устойчивой системой отсчёта, общей у человека и животных. Руководствуясь" схемой тела", наблюдатель ориентируется в окружающем его пространстве относительно расположенных в нём объектов. Он выделяет пространственные соотношения с учётом собственного положения (ближе дальше, справа слева, спереди сзади, сверху-снизу и т. п.). Назовём условно этот тип связей "субъект- объект" (S-O). В целом ряде случаев взаимодействие объектов материального мира происходит и без участия субъекта. В этих случаях учитываются пространственные зависимости между самими объектами, позиция наблюдателя (субъекта) при этом не играет существенной роли. Назовём условно этот тип связей "объект - объект" (О-О). Выделение этих двух типов связей носит не абсолютный, а относительный характер, так как субъект, временно выключаясь из целостной системы пространственных отношений, постоянно присутствует в ней. Он не только изменяет своё положение в окружающем пространстве благодаря способности к передвижению, но и активно взаимодействует с объектами, оказывая тем самым решающее влияние на обнаружение пространственных связей между самими объектами, преобразуя их. Поэтому отражение пространственных свойств и отношений носит динамический характер.
Особенностью пространственных связей, как подчеркивал Б. Г. Ананьев, является то, что это есть один из видов отражения отношений между объектами. Поэтому они могут быть выявлены и использованы лишь в ходе активной преобразующей деятельности субъекта, благодаря которой из объекта как бы "вычёркиваются" (С. Л. Рубинштейн). Нужные пространственные связи и отношения, непосредственно не заданные в самом объекте познания.
Таким образом, пространственное мышление выполняет весьма важную гносеологическую функцию и обладает ярким качественным своеобразием.
Пространственное мышление - вид умственной деятельности, обеспечивающий создание пространственных образов и оперирование ими в процессе решения практических и теоретических задач. Это сложный процесс, куда включаются не только логические (словесно-понятные) операции, но и множество перспективных действий, без которых мышление протекать не может, а именно опознание объектов, представленных реально или изображённых различными графическими средствами, создание на этой основе адекватных образов и оперирование ими по представлению. Являясь разновидностью образного мышления, пространственное мышление сохраняет все его основные черты, и тем самым отличается от словесно-дискурсивных форм мышления. Это различие мы видим прежде всего в том, что пространственное мышление оперирует образами; в процессе этого оперирования происходит их воссоздание, перестройка, видоизменение в требуемом направлении. Образы здесь являются и исходным материалом, и основной оперативной единицей, и результатом мыслительного процесса. Это не означает, конечно, что при этом не используются словесные знания. Но в отличие от словесно-дискуссивного мышления, где словесные знания являются основным содержанием, в образном мышлении слова используются как средства интерпретации уже выполненных в образах преобразований.
Будучи более тесно и непосредственно связанным с отражением реальной действительности, образ даёт знание не об изолированных сторонах (свойств) этой действительности, а представляет собою целостную мысленную картину конкретного участка действительности, где воспроизводятся не отдельные признаки и свойства объектов, а обязательно их пространственная размещённость.
Для создания образа, как мысленной картины существенным моментом является выбор исходной точки отсчёта, что также отличает образ от понятия (словесного знания). Итак, пространственное мышление, обладая всеми характерными особенностями образного мышления, выполняет специфическую функцию в познании и обучении. Оно позволяет вычленять из реальных объектов, теоретических (графических) моделей пространственные свойства и отношения, делать их объектом анализа и преобразования. Основной оперативной единицей пространственного мышления являются пространственные образы, в которых отражаются не все свойства, признаки предметного мира, а лишь пространственные свойства и отношения. Пространственное мышление, в своих наиболее развитых формах формируется на графической основе, поэтому ведущими для него являются зрительные образы.
Анализ гносеологических и психологических особенностей пространственного мышления важен для определения основных направлений и перспектив его развития у школьников. Изучая содержание пространственного мышления школьников, имеется в виду, что и практически, и теоретически оно формируется в основном на материале евклидова пространства, при рассмотрении разных инерционных систем, где действуют законы классической физики и механики, теории тяготения. Наряду с ними в школе закладываются основы научных представлений о пространстве, отражающие зависимости, существующие в неинерционных системах, где не действуют классические законы механики и земного притяжения. На уроках физики старшеклассники знакомятся с элементами ядерной физики, теории относительности, изучают законы не только макро, - но и микромира. Аналогичные тенденции проявляются и на уроках по другим предметам.
Развитию пространственного мышления необходимо уделять больше внимания, чем это предусматривается в учебниках, поэтому мы ставим перед собой задачу, разработать элементы методики формирования пространственного мышления у учащихся основной школы, которые будут в себя включать упражнения в определённой системе, о которых будет говориться ниже, а также попытаться на основе того материала, который имеется в учебнике, так организовать работу с детьми, чтобы она способствовала развитию пространственного мышления.
Глава II. Методика формирования пространственного мышления учащихся основной школы при изучении векторного пространства
2.1 Методические аспекты развития пространственного мышления как элемента образного
Рассмотрим, какие подходы предлагают для развития пространственного мышления в средней школе и выясним возможности их использования.
А. Пардала выделяет такие основные типы упражнений, дидактическим назначением которых является формирование и развитие пространственных представлений учащихся: математические игры, связанные с пространственными представлениями; исследование конкретных геометрических объектов-фигур и преобразований; конструктивные задачи; прикладные задачи; проекционные стереометрические задачи; задачи на проектирование геометрических тел, построение сечений; диагностические задачи на проверку сформированности пространственных представлений.
Однако А. Я. Цукарь считает, что хотя это не классификация, тем не менее так смешивать (как это сделал А. Пардала) в одном перечне типы упражнений, одни из которых являются частным случаем других, а у некоторых совершенно разные основания, непозволительно. Очевидно, что выделять в отдельный тип диагностические задачи не имеет смысла. В математических играх могут использоваться самые разные задачи: и на проектирование, и на построение сечений. А разве задачи на проектирование геометрических тел не являются конструктивными? Налицо частая для методических публикаций нечётность в делении, как логической операции, иногда доходящая до эклектики.
Г. Н. Никитина говорит о методических приёмах развития пространственного мышления учащихся: привлечение неплоских пространственных образов при рассмотрении вопросов планиметрии; создание целостного геометрического образа с опорой на наглядность; создание ситуаций, способствующих активному оперированию геометрическим образом; творческое конструирование новых геометрических образов. В другой работе Г. Н. Никитина с авторам к показателям развития пространственного мышления относит умения: 1. создавать исходный геометрический образ, т. е. в графической модели передавать форму, размеры и взаимное расположение отдельных элементов объекта; 2. выбирать и произвольно изменять точку отсчёта; 3. сохранять в памяти геометрический образ; 4. анализировать и синтезировать геометрические образы; 5. рассматривать объект с разных точек зрения; 6. мысленно производить различные геометрические преобразования над исходным геометрическим образом; 7. мысленно изменять структуру геометрического образа; 8. осуществлять глазомерные оценки линейных и угловых величин. В приведённых выше делениях также имеется смешение разных оснований.
На каком-то этапе специалисты, образно говоря, занимаются "собирательством", чтобы затем более внимательно изучить и систематизировать накопленный материал. В последнее время появилось понимание того, что не только 5-6 классы среднего звена, а также и начальная школа, - благоприятное время для развития пространственного мышления. Поэтому хоть и медленно, но на уроке математики в начальных классах проникают специальные упражнения, направленные на его развитие. Затем в 6-9 классах эта проблема забывается и всплывает (по необходимости) в 10 классе, поскольку явно даёт о себе знать. Традиционно для развития пространственного воображения учеников 10-11 классов использовались задачи на построение сечений многогранников плоскостью. Эта тема находилась в центре внимания многих исследователей, начиная с Н. Ф. Четвертухина. Ей посвятил свою небольшую книгу К. С. Богушевский, которая помогла учителям увидеть место таких задач при изучении аксиом стереометрии и тем " Параллельность прямых и плоскостей ". Методистами разрабатывались системы задач, связанных с изображением пространственных фигур и с построением сечений многогранников плоскостью.
Основой формирования пространственного воображения является практическая работа ребёнка с пространственными объектами, манипулирование ими, изменение их положения в пространстве разъединение и соединение нескольких в один. Внешние действия субъекта с объектами являются необходимыми для того, чтобы он мог затем производить с ними внутренние, мысленные действия. Но они не являются достаточными. Любая деятельность воображения невозможна без фиксации её промежуточных этапов (конструкций) каким-либо простым способом (в знаково-символической форме). Поэтому для развития пространственного воображения школьников нужно вооружать их соответствующими знаниями о способах такой фиксации. Одним из самых распространенных является изображение пространственных объектов по принятым правилам. Необходимое условие формирования и развития пространственного воображения - наличие достаточно обширного и разнообразного материала для восприятия. Правильность, продуктивность его возрастает под влиянием упражнений, учитывающих всю гамму возможных операций над пространственными объектами, приводящих к созданию новых образов, ведь основная его функция - оперирование пространственными образами. Таким образом, явно выделяются два типа упражнений, лежащих в основе формирования и развития пространственного мышления : упражнения на умение читать изображения и изображать пространственные объекты, и упражнение на оперирование пространственными образами. В свою очередь, в них можно выделить разные виды: отыскание изображения из нескольких данных для предъявленного объекта; нахождение объекта из некоторого набора, соответствующего данному изображению; завершение изображения известного объекта по его фрагменту; идентификация различных изображений одного и того же пространственного объекта; узнавание фигуры по её проекциям; 6. определение взаимного расположения нескольких фигур по их изображениям; 7. оценивание формы и размеров фигуры; 8. построение проекций заданной фигуры; 9. построения изображения объекта по его 10. изображение объекта по его описанию; 11. изготовление модели по её чертежу, по предъявленному объекту, по его описанию; 12. узнавание и изображение объекта, полученного (мысленным) изменением ( с помощью поворота, симметрии, параллельного переноса) положения заданного; 13. узнавание и изображение фигуры, составленной из заданных по известному правилу; 14. изображение пересечения заданных фигур (в том числе после мысленного их перемещения); 15 изображение частей фигур после её мысленного расчленения.
Требования к содержанию (упражнениям) обучения, направленного на достижение необходимого уровня пространственного мышления (по Нурмагомедову). Упражнения должны строиться с расчётом: - использования конкретных представлений о материальных телах , их взаимном расположении в пространстве, об их свойствах (подвижность, неподвижность, устойчивость, неустойчивость, способность сохранения и изменения формы и т. п. ); учёта необходимости доминанты качественной оценки окружающих предметов над количественной, свойственной учащихся основной школы. Отсюда, например метрические представления не должны опережать представления о форме или взаимном расположении; обеспечения необходимой и обязательной работы по развитию речи, формированию активного словаря, характеризующего форму предметов и фигур, их свойств, отношения взаимного расположения в пространстве; - обеспечения использования при выполнении заданий и упражнений всех возможных рецепторов восприятия окружающего пространства (зрения, осязания, слуха). Отсюда необходимость обеспечения при решении упражнений разнообразных видов деятельности и способов решений.
2.2 Методика формирования пространственного мышления учащихся основной школы при изучении элементов геометрии
Известно, что геометрия как наука, первоосновы которой излагаются в школе, имеет своим предметом изучение пространственных форм и отношений реального мира. Научное познание этих форм и отношений возможно при наличии у человека развитого мышления и воображения. Такие качества приобретаются жизненным опытом и обучением. Отсюда важнейшей целью обучения школьной геометрии является формирование пространственных представлений и развитие воображения и мышления у учащихся.
При обучении геометрии её цели и средства находятся в сложных диалектических причинно- следственных взаимосвязях. Если ученик при решении геометрических задач плохо представляет формы фигур и их детали, он допускает ошибки или совсем теряется в преодолении трудностей. Это показатель того, что у него слабо развиты пространственные представления и воображение. Раскрытие этих взаимосвязей с учётом индивидуальных способностей школьников является важнейшей проблемой педагогики геометрии. Формирование геометрических представлений и развитие пространственного мышления учащихся на материале школьного курса геометрии преследует не только общеучебные, но и теоретико-познавательные цели - подвести учащихся к пониманию существенных свойств реального пространства(симметричность, подобие, конгруэнтность в себе, непрерывность и прерывность, трёхмерность, бесконечность и др. ), знаниями которых они могли бы пользоваться в трудовой деятельности.
Процесс познания пространственных форм и отношений протекает у человека всю его жизнь, целенаправленный смысл ему придаётся лишь при обучении в школе, поэтому, занимаясь этими вопросами на уроках геометрии, следует тщательно учитывать уровень и характер формированности этих качеств у ребёнка и на каждом последующем этапе, предшествующем данному.
Для достижения рассматриваемых учебных целей геометрии возможно пойти двумя путями: -
совершенствовать содержание школьной программы;
- применять систему методов, средств и форм организации учебной деятельности учащихся.
Известно, что процесс формирования и развития пространственных представлений у человека проходит эмпирическую и абстрактную логико-геометрические ступени. При этом вторая почти полностью определяется и зависит от школьного геометрического образования (программы и методов). За последнее десятилетия жизненные условия (на экономической ступени) для познания свойств пространства учащимися основной школы значительно обогатились и расширились под влиянием изменений их "коммуникационного, визуального и метрического климата". Практически все учёные-исследователи указывают на особую роль геометрии, геометрического материала в развитии мышления школьников. Так, например А. Пышкало в числе важнейших методических линий выделяет формирование геометрических представлений, развитие мышления, формирование пространственных представлений и воображения. В своей диссертации А. Пышкало говорит, что в процессе изложения материала у учащихся формируются навыки индивидуального мышления, воспитываются умения делать простейшие индуктивные умозаключения. Одновременно с этим постепенно развиваются и используются навыки дедуктивного мышления. Всё это ведётся через формирование приёмов умственных действий таких, как анализ и синтез, сравнение, абстрагирование, обобщение.
В первом классе ведётся работа по первоначальному ознакомлению с фигурами. Уже при этом дети выполняют умственные операции анализа и синтеза. Важной задачей методики обучения в этот момент является обеспечение целенаправленного и полного анализа фигуры, на основе которого выделяются её существенные свойства и происходит отвлечение от несущественных свойств. В ходе такой работы с необходимостью возникает потребность применения геометрической и логической терминологии, символики, условных изображений. Их введение поэтому не может являться формальным актом. В традиционном обучении уже в первом классе часто начинают изучение фигур с введения формального определения. Эксперимент показал, что использование формальных определений в первом классе оказывается преждевременным. Но уже в третьем классе, когда дети овладели значительным запасом представлений, возникает потребность в обобщениях, учащиеся уже должны уметь давать описание фигур и их свойства по своему характеру близкие к определениям.
Одна из задач в разработке методики изучения геометрического материала А. Пышкало состояла в исследовании возможности осуществления первоначального ознакомления учащихся третьих классов со структурой логического следования. С этой целью в диссертации Пышкало намечены специальные упражнения. Основу работы по формированию пространственных представлений составляет прежде всего создание запаса пространственных представлений, получаемых на основе непосредственного знакомства с материальными образами геометрических объектов, которые в дальнейшем совершенствуются с привлечением геометрических моделей. На базе создания запаса представлений уже во вторых - третьих классах становится возможным формирование собственно пространственных представлений, когда новые пространственные представления создаются как комбинация ранее созданных.
Важным методическим приёмом, обеспечивающим прочные геометрические знания является формирование пространственных представлений через непосредственные восприятия учащимися конкретных вещей, материальных моделей геометрических образов. В первом классе пространственные представления вырабатываются в процессе приобретения детьми практического опыта пространственной ориентировки реальных предметов, материальных моделей геометрических фигур. Во втором - третьем классе характер работы по формированию пространственных представлений усложняется. Следует, например, формировать представления об одной фигуре с опорой на непосредственное восприятие другой фигуры. Например, представление о кубе с опорой на непосредственное восприятие модели квадрата, изготовленного из палочек и пластилина. Дети изготовили такую модель. На некоторое время учащимся показывается модель куба, и после того, как она убрана ставятся вопросы: "Можно ли из палочек и кусочков пластилина изготовить модель куба? Сколько для этого нужно взять палочек, сколько кусочков пластилина? " Учащиеся решают эту задачу мысленно, в воображении. В диссертации разработана система упражнений и методика их использования, основным назначением которых является формирование пространственных представлений и развитие пространственного мышления и воображения учащихся.
Однако, несмотря на декларируемый развивающий характер методики А. Пышкало, с точки зрения современных психологов изучение сначала плоских, а затем объёмных фигур является неверным. Данные психологических и физиологических исследований указывают на интенсивное обогащение пространственных представлений у учащихся основной школы, увеличение числа выполняемых ими пространственных операций передвижение, размещение, воссоздание форм, а также расположений ближе, дальше, рядом, вместе, раздельно и др. Эти представления и операции имеют ярко выраженный качественный, а не количественный метрический характер. Умственная деятельность учащихся основной школы проходит прежде всего в формах установления связей между его опытом в физическом пространстве и конкретным действием. Поэтому первоначальное ознакомление учащихся с основными геометрическими понятиями (форма, тело, поверхность, плоскость и др.) нужно проводить на материале, с которым школьник может оперировать своими руками. Замечено также, что у детей формируются раньше некоторые топологические, потом проективные, а позже - метрические понятия и свойства фигур. При разработке содержания программы начального обучения нельзя не учитывать указанной последовательности психологического развития ребёнка.
Важнейшей педагогической проблемой является разрешение противоречия между первичностью пространственных форм с точки зрения процесса познания мира, их физическим реализмом сравнительно с абстрактностью плоских фигур и традиционной логикой построения геометрических курсов, развивающихся от плоской и пространственной геометрии.
2.3 Методика формирования пространственного мышления учащихся основной школы при построении модели к задачам
В нашей стране обучение математике сложилось таким образом, что около 40% содержания всего материала учебников по математике для начальной школы составляют текстовые задачи. И значительная часть времени на уроках математики отводится решению. Поэтому осуществление направленности этой части уроков на формирование пространственного мышления учащихся основной школы будет играть важную роль в становлении и развитии учащихся.
В анализах ежегодных проверок качества обучения математике в начальной школе постоянно отмечается не умение значительной части учащихся решать текстовые задачи. Изучение опыта работы массовой школы показывает, что многие учителя ориентируют учащихся в работе над задачей на достижение единственной цели - получение ответа на вопрос задачи.
Чему дети при этом учатся или должны научиться, не всегда осознаётся даже учителем, а потому такое обучение зачастую носит случайный характер. В методике преподавания математики, в психологии разработаны вопросы теории решения задач, а именно: определены в целом этапы решения задачи, описаны некоторые методы и способы решения, разработаны нормативные формы записи и т. п. Однако накопленные в методике знания о задачах и их решении не стали ещё предметом специального обучения школьников. Одной из причин этого является недостаточное понимание учителем роли текстовых задач в обучении учащихся основной школы.
Методика решения текстовых задач была разработана С. Е. Царевой. Ею были сформулированы этапы решения текстовых задач: Восприятие и осмысление. Поиск плана решения. Решение задачи. Проверка решения задачи. Ответ задачи.
Для определения роли текстовых задач в формировании пространственного мышления учащихся начальных классов современной школы выясним на каком этапе решения текстовой задачи есть возможность формировать пространственное представление у учащихся основной школы.
Существуют различные методы решения текстовых задач, но при развитии пространственного мышления более важную роль будут играть решения задач геометрическим методом или хотя бы построение такой модели к задачи как чертёж. Моделирование играет значительную роль во всех разделах науки, а в связи со стремительным внедрением в различные области человеческой деятельности компьютеров эта роль ещё более возрастает. Включение моделирования в учебный процесс, обучение моделированию - важная задача современной школы. Использование моделей при решении задач включает в себя построение модели, составление по ней плана решения и его выполнение как на языке моделей, так и другими средствами. Построение модели - есть средство осмысления содержания задачи.
Известны различные виды (приёмы) моделирования. Наиболее простым является практическое воспроизведение описанной в задаче ситуации (этот способ иногда называют "драматизацией" задачи). Рассмотрим такую задачу: "У Серёжи было 7 марок, а у Саши 3 марки. Сколько марок у мальчиков вместе?" Для формирования пространственного воображения эту задачу можно воспроизвести так. К доске выдут два мальчика. У одного будет 7 марок (вместо марок можно использовать небольшие квадратики из бумаги), а у другого - 3. Такое воспроизведение дополняет представления детей, возникшие при чтении текста задачи.
Полезно научить первоклассников осознанно использовать приём драматизации. Обучение воспроизведения заданной ситуации должно проводиться параллельно с формированием у учащихся умения представлять её. Строиться это обучение должно так, чтобы учащиеся переходили от практической деятельности к учебной. В большинстве случаев прямое повторение того, что описано в задаче, невозможно, поэтому целесообразнее мысленное её представление или изображение с использованием произвольных предметов: квадратов, кружков палочек и т. п. Это и есть начало работы над обучением школьников предметному моделированию как средство осуществления первичного анализа.
К условно-предметным моделям отнесём схематические рисунки. Предметы, о которых идёт речь в задаче, изображаются в этом случае кружочками квадратиками и т. п.
Построение чертежа (геометрической модели) может быть полезно при анализе и поиске решения задач, содержащих как непрерывные величины, так и дискретные. Например, для задачи "В коробке было 40 конфет. Сначала оттуда взяли 10 конфет, а потом ещё 5 конфет. Сколько конфет осталось в коробке?" Воспользуемся чертежом, что будет формировать у детей пространственное представление. 40к. 5к. 10к.?
Для развития пространственного мышления у учащихся воспользуемся темами некоторых уроков, в которых нет явного задания на формирование пространственного воображения, но через чертёж, схему при правильно выбранных учителем целей задания, можно развивать его.
Одна из тем такого урока (третья четверть): "Применение чертежей при решении задач". Вначале учащимся целесообразнее предложить выполнить ряд подготовительных упражнений. Одно из них, например, такое:
"Покажите отрезок, длина которого известна. Как можно найти её через длины других отрезков?" (чертежи заранее вычертить на доске). 7 см. 3 см.
А) 6 см. 6 см. 3см.
Б)? 1 см. 3см.
В) ? 5 см.
? Г) 2 см. 4 см.
Для того чтобы научиться решать задачи, полезно научиться строить чертежи к задачам и составлять планы решения по чертежам.
Поиск плана решения задачи можно осуществить на основе её модели. Модель может служить только осмыслению содержания задачи, а может быть использована и для поисков плана решения. Поиск плана решения задачи по её модели заключается в выделении элемента, моделирующего искомое, в определении последовательности операций с другими элементами модели или соответствующей последовательности арифметических действий над данными и неизвестными для получения искомого или для составления уравнения. Для осуществления поиска плана решения задачи по чертежу, чертёж должен быть построен. Операция построения может включаться как в первый этап решения (если чертёж строится для лучшего понимания задачи), так и во второй этап (если содержание задачи понятно и без чертежа). Поэтому обучение детей построению чертежа к задачам - важная часть обучения использования чертежа как средства поиска плана решения.
Приведу лишь несколько примеров:
1. Из каких отрезков состоит искомый отрезок. Сумме или разности данных чисел равна его длина?
А) 3 см. 7см. 10 см.
Б) 3 см. 7 см. 2.
По данным чертежам составьте выражения, значения которого соответствуют знаку"?" чертеже. 15 см.
А) 5 см. ? 5 кг.
Б) ? 7 кг. 12 кг.
В обучении поиск плана решения с помощью разбора задачи и построения графических схем стал предметом специального изучения и овладения учащимся во второй половине третьей четверти. В дальнейшем, на протяжении всего учебного года учитель достаточно часто должен предлагать учащимся осуществлять поиск плана решения таким способом.
При решении задач геометрическим методом, при построении чертежей, моделей к задачам происходит развитие пространственного мышления у детей, т. к. ребёнок постоянно сталкивается с различными геометрическими понятиями, объектами, с отношениями этих геометрических объектов между объектами в пространстве.
Заключение
В заключении подведем основные итоги. На основании изученного материала можно сделать следующие выводы.
Формируются пространственные представления у учащихся 9-11 классов в процессе обучения преимущественно путём:
1. наблюдения;
2. восприятия и осмысливания информации, полученной от учителя и из учебников;
3. практической деятельности (измерение, построение, рисование, моделирование, решение задач и др.);
4. мысленного оперирования пространственного представления.
На основе длительных теоретических и экспериментальных исследований для определения сформированности у учащихся пространственного представления, их полноты, осмысленности, действительности, научности, в качестве критерия оценки Н. Д. Мацко предлагает принять следующие умения:
1. Распознавать данный объект среди объектов реальной действительности.
2. Распознавать объект среди изображений.
3. Устанавливать взаимосвязи между словом, представлением изображением и объектом реальной действительности.
4. Воспроизводить в воображении объект (представления памяти).
5. Воспроизводить представления памяти (словесно, графически, в виде модели).
6. Создавать в воображении новые объекты (представление воображения).
7. Воспроизводить представления воображения (словесно, графически , в виде модели. )
На основе этих умений ею же определяются уровни сформированности пространственного представления у учащихся.
Уровень I (Аккумулятивный). Накопление и узнавание пространственных признаков и отношений. Учащиеся накапливают разнообразные пространственные представления, учатся узнавать разнообразные пространственные объекты, их отдельные признаки и отношения. Они могут дать название объекту, найти его на рисунке среди предметов реальной действительности. Но дифференцирована между различными категориями пространственных признаков неустойчива, часто отсутствует соответствие между образом и словом и наоборот. Представления у учащихся неполные (умение 1-4).
Уровень II (Репродуктивный). Воспроизведение представления памяти. У учащегося развита способность воспроизводить (в представлении, словесно, на рисунке, в виде модели) известные им пространственные признаки и отношения. У них значительно расширился запас пространственной терминологии, накоплены разные виды пространственного представления и отношений: учащиеся, умеют устанавливать связи между пространством, количествами и временными представлениями. Слово уже приобретает сигнальное значение и вызывает у учащегося соответствующее представление (умение 1-5)
Уровень III (Конструктивный). Самостоятельное конструирование пространственного образа. Учащиеся активно используют как опору в мыслительной деятельности уже оформленные представления в синтезе с количественными и временными отношениями. Они умеют давать словесное описание пространственных признаков и отношений, опираясь на отдельные элементы пространственных понятий (о форме, величине, расстоянии и др.) На основе сформированных пространственных представлений они создают новые представления и оперируют ими, пользуясь словесным описанием, числовыми данными, рисунками (умение 1-5, частично 6, 7).
Уровень IV (Интеллектуальный). Мысленное оперирование пространственными представлениями. У учащегося богатый запас пространственного представления, терминологии, они легко дифференцируют пространственные признаки и отношения. Для этого уровня характерно уже умение перемещать мысленно пространственные объекты (симметрия, перенос, поворот), находить на рисунке положение фигуры после её перемещения, вид перемещения и т. д. (умение 1-7)
Уровни не относятся конкретно к определённым классам и не рассматриваются изолировано, как временные периоды, которые строго переходят один в другой. Уровни между собой тесно связаны, переплетаются и можно полагать, что каждый предшествующий является основной, подготавливающей последующий. При формировании пространственного представления эти уровни могут сосуществовать при оперировании разным содержанием у одних и тех же детей и одним и тем же содержанием у разных детей. Особое место в формировании представлений отводится чтению и построению графических изображений. При построении графического изображения главной задачей является перевод представления об объекте в плоскостное его изображение, при чтении решается противоположная задача: на основе восприятия плоскостного изображения мысленно, в представлении, воспроизводится форма, размеренность, положение объекта и выясняются необходимые сведения, взаимосвязи и отношения. Представления об объекте при чтении и построении графических изображений формируются не только в результате непосредственного узнавания или припоминания, а в результате целой системы умственных действий, направленных на преобразование данных восприятия и мысленное воспроизведение образа. Чтение и построение нельзя свести непосредственно к навыкам, они являются осмысленными умениями, в которых лишь отдельные действия автоматизированы.
Школьными учебными программами предусмотрено овладение учащимися 9-11 классов почти всеми пространственно - геометрическими представлениями, словами - терминами и символами, необходимыми для усвоения учебного материала в основной школе.
Результаты констатирующего эксперимента показали, что запас сформированных пространственных представлений у учащихся по окончании 9 класса недостаточный, существует несоответствие между требованиями программы и уровнем сформированности пространственных представлений у учащихся. Нередко у учащихся (25,7%)наблюдается расхождение между представлением и словесным описанием, отсутствие достаточно развитой зрительной памяти (28, 4%), сформированные образы инертны и малопригодны для конструктивных видоизменений (31, 5%), представления приведены в "умах" учащихся в систему и др. Одной из причин недостаточной сформированности пространственных представлений у учащихся является то, что при существующей методике преподавания формируются пространственные представления не в достаточной мере целенаправленно, являясь часто лишь побочным продуктом обучения.
На основе полученных данных результатов теоретического анализа и констатирующего эксперимента, мы пришли к выводу, что формирование пространственных представлений у учащихся будет обеспечено лишь тогда, когда в педагогическом процессе будут созданы новые условия для: 1. запоминания; 2. накопления учащимися запаса пространственных представлений; 3. опыта распознания пространственных признаков и отношений; 4. запаса словесных знаний и терминологии; 5. приобретения умений устанавливать взаимосвязи между объектом, словом, образом и предметом реальной действительности; 6. умений воспроизводить представления (в воображении, мысленно графически в виде модели) и создавать новые; 7. мысленного оперирования представлениями (представления воображения), используя их как опору при усвоении знаний; 8. приведение сформированных представлений в систему.
Один из путей реализации этих условий мы видим в обоснованной системе упражнений, которая обеспечивала бы целенаправленность процесса формирования пространственных представлений.
Список литературы
1. Байрамукова П.У. Схематический рисунок при решении задач // Начальная школа – 2001 - №11
2. Волович Н. Б. Наука обучать: психология преподавания математики. М., 2002.
3. Выготский Л. С. Воображение и творчество в детском возрасте. М., 2001.
4. Глейзер Г. Д. Методы формирования и развития пространственных представлений школьников в процессе обучения геометрии. М., 2002.
5. Григорян К. Некоторые особенности процесса образного мышления. М., Знание, 2002.
6. Груденов Я. И. Психолого-дедуктивные основы методики обучения математике. М., 2001.
7. Давыдов В. В. Виды обучения в обучении. М., 2001.
8. Зинченко В. П., Моргунов Е. Б. Человек Развивающийся. М., 2001.
9. Корнфельд С. Методические рекомендации к проверке сформированности пространственных представлений учащихся. М., 2000.
10. Крутецкий В. А. Психология математических способностей учащихся основной школы. М., 2000
11. Крутецкий В. А. Основы педагогической психологии. М., 2001.
12. Леонтьев А. Н. Деятельность. Сознание. Личность. М., 2001.
13. Мацко Н. Д. Формирование пространственных представлений у учащихся I-IV классов в процессе обучения. Киев, 2002.
14. Нурмагомедов Д. Методика формирования пространственных представлений у учащихся основной школы. М., 2000
15. Пиаже Ж. Как дети образуют математические понятия. Вопросы психологии, М., 2001.
16. Подходова Н.С. Геометрия // Начальная школа, - 2001 - №1 – С 14-15
17. Психологические возможности учащихся основной школы в усвоении математики / под ред. В. В. Давыдова. М., 2000.
18. Пышкало А. М. Вопросы формирования геометрических представлений у учащихся основной школы. М., 2001
19. Скаткин Л. Н. Лекции по методике начального обучения математике. М., 2001
20. Фридман Л. М. Психолого-педагогические основы обучения математике в школе. М., 2001.
21. Фуше А. Педагогика математики. М., 2001.
22. Цукарь А. Я. Теоретические основы образного мышления и практика их использования в обучении математике. Новосибирск, 2002.
23. Якиманская И. С. Возрастные и индивидуальные особенности образного мышления. М., 2001.
24. Якиманская И. С. Развитие пространственного мышления школьников. М., 2001.
[1]
Леонтьев А. Н. Деятельность. Сознание. Личность. М. , 2001. - С. 23
[2]
Давыдов В. В. Виды обучения в обучении. М. , 2001. – С. 423
[3]
Пиаже Ж. Как дети образуют математические понятия. Вопросы психологии, М., 2001. –С. 133
[4]
Пиаже Ж. Как дети образуют математические понятия. Вопросы психологии, М., 2001. –С. 72-83
|