Учреждение образования
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ
УНИВЕРСИТЕТ
СРАВНИТЕЛЬНЫЙ АНАЛИЗ МЕТОДИКИ ОЗНАКОМЛЕНИЯ С РАВЕНСТВАМИ,
НЕРАВЕНСТВАМИ, УРАВНЕНИЯМИ В
ТРАДИЦИОННОЙ ШКОЛЕ И СИСТЕМЕ
РАЗВИВАЮЩЕГО ОБУЧЕНИЯ
ДИПЛОМНАЯ РАБОТА
СТУДЕНТКИ 4 КУРСА
ФАКУЛЬТЕТ ПиМНО
БГПУ
НАУЧНЫЙ РУКОВОДИТЕЛЬ
____________________________
УЧ. СТЕПЕНЬ, ЗВАНИЕ
____________________________
Ф.И.О.
ЗАЩИЩЕНА
с оценкой отл
|
|
МИНСК 2003
Содержание........................................................................................... 2
Введение.................................................................................................. 3
Глава 1. Система развивающего обучения Д.Б. Эльконина — В.В. Давыдова.................................. 5
Глава 2. Сравнительный анализ методики ознакомления с равенствами, неравенствами, уравнениями в традиционной школе и системе РО............................................................................................. 12
2.1. Непосредственное сравнивание предметов........ 13
2.2. Моделирование отношений равенства и неравенства:............................................................................................................. 15
2.3. Подбор величин по формулам равенства и неравенства............................................................................................................. 20
2.4. Переход от неравенства к равенству и наоборот 23
2.5. Как из частей составить целое.................................... 26
2.6. Что такое уравнение?.......................................................... 28
2.7. Методика обучения решению текстовыхзадач 31
2.8. Диагностика и контроль в системе РО.................... 35
Заключение........................................................................................ 36
Литература.......................................................................................... 38
Развитие
— ключевое слово всей дипломной работы.
Что же такое развитие?
Развитие
— это самостоятельный процесс, но протекает оно в формах общения, присвоения, обучения и воспитания [5, 319].
Проблема исследования:
каковы педагогические условия реализации задач общего развития младших школьников в педагогической системе РО на уроках математики; в чем сходство и различие методики обучения математики в традиционной школе и системе РО, на примере темы “Числовые равенства, неравенства, уравнения”.
Реклама

Решение этой проблемы составляет цель исследования
.
Гипотеза исследования:
— общее развитие детей достигает более высоких результатов если будут реализованы следующие условия:
— выделение ведущих приоритетных идей системы РО, которые соответствуют современным задачам образования и развития учащихся начальной школы;
— обоснование педагогических условий организации процесса обучения и воспитания младших школьников и реализации задач общего развития школьников.
Реализация поставленной цели требует решения совокупности задач:
— выделить систему приоритетных идей В.В. Давыдова-Эльконина адекватную современным условиям начального образования и организовать опытно-экспериментальную работу по реализации задач общего развития младших школьников в современных условиях начального образования;
— сформировать требования к процессу организации урока, направленные на общее развитие младших школьников;
— опираясь на результат исследования, разработать рекомендации по реализации задач общего развития в обучении младших школьников.
Предмет исследования — процесс обучения детей по системе РО.
Объект исследования
— система РО в современных условиях обучения школьников в начальной школе.
Исторически сложившаяся классическая система школьного образования при всем разнообразии ее форм подчинена задаче усвоения учащимися определенной суммы знаний, умений и навыков.
С 1990 года Законом об образовании определены первостепенные цели:
“… Обеспечить начальный этап развития личности; выявить и обеспечить развитие способностей; формировать умение и желание учиться, приобрести необходимые умения и навыки учебной деяте6льности; обучиться чтению, письму, счету; овладеть основами теоретического мышления; культурой речи и поведения; основами личной гигиены и здорового образа жизни”.
В последние годы как теоретики, так и практики нашего образования все больше внимания уделяют приемам развивающего обучения. Этим проблемам посвящены серьезные научные труды, их стремятся решать с помощью различных особых учебников и методических пособий. Это свидетельствует о том, что проблемы интеллектуального, нравственного и физического развития школьников весьма актуальны
в нашем образовании.
В сложившейся у нас системе образования долгое время доминировал обезличенный подход к учащимся. То, что мы называли образованием, не более чем накапливание информации с опорой на вторичную функцию мозга — память, в то время как его основной функцией является мышление. В процессе обучения (математике или физике) мы чаще всего связываем мышление с решением задач, которые предполагают полный ответ. Они могут быть либо верными, либо неверными, однако сам ответ и его форма нередко значат для ученика и учителя больше, чем способ его получения, чем логические рассуждения на пути к нему, что фактически обесценивает мыслительный процесс. Гораздо реже детям предоставляется возможность задумываться над тем, как может быть получен тот или иной результат, как самому придумать такую же задачу, как научить других придумывать и решать те или иные задачи, всегда ли может быть получен однозначный правильный ответ.
Реклама

Дети, которые приходят в школу с представлением о том, что на многие вопросы можно ответить по-разному, вскоре эту уверенность теряют. В традиционной школе детей фактически приводят к мысли, что на уроке главное — правильные ответы, ничто иное не имеет ценности по сравнению с правильным ответом, а основной их источник — учителя или учебники. Однако в демократической школе, как и в демократическом обществе, многие проблемы не имеют однозначных решений.
“Процесс постановки проблем, поиска РАЗУМНЫХ альтернатив и реализация наилучших решений, — считает американский ученый У. Глассер, — и есть подлинный процесс демократического образования. Развитая память еще не есть образованность, точная информация еще не есть знания. Определенность и механическое зазубривание, запоминание — враги живой мысли, они убивают творчество и сводят на нет оригинальность мышления”.
Откройте наши учебники математики, и вы увидите традиционное зазубривание, например таблицы умножения и сложения и многое другое.
Конечно ребенку и в традиционной школе приятно отвечать правильно, но, если точность ответа основана лишь на механическом запоминании, это не приносит истинной радости познания. Мы лишь тогда испытываем настоящее удовлетворение, когда наша правота является результатом самостоятельных рассуждений, собственного мнения и принятия соответствующего решения. Реализация такого подхода к обучению, при котором ребенок живет с ощущение пусть маленького, но личного успеха, испытывая при этом и уверенность в себе, составляет суть РО.
“Либо человек живет с ощущением успеха, испытывая уверенность в себе и внутреннее удовлетворение, либо считает себя неудачником, отчаянно пытаясь избавиться от преследующего его чувства психологического дискомфорта” (У. Глассер). Не это ли создает предпосылки для его конфронтации с обществом в форме преступности или ухода в себя? А ведь ни один ребенок не должен иметь в школе клеймо неудачника.
Обычная школа со своим упором не на развитие мышления, а на запоминание и механическую зубрежку провоцирует неуспеваемость и поэтому она больше всего бьет как раз по детям, которые получили хорошую дошкольную подготовку. Если до школы взрослые радовались их интересным словам и выражениям, бесконечным “почему?”, изобретательности в прямом и переносном смысле, то, придя в школу, дети вдруг обнаруживают, что успех может быть обеспечен в основном хорошей памятью, а не умением мыслить, высказывать идеи, творчески подходить к заданию, учиться с интересом.
РО создает условия для того, чтобы научить детей думать.
“Взрослые никогда ничего не понимают сами, а для детей очень утомительно без конца им все объяснять и растолковывать.”
А. де Сент-Экзюпери.
Глава 1. Система р
азвивающего обучения Д.Б. Эльконина — В.В. Давыдова
Про необходимость изменения приоритетов начального образования заговорили в 50-60 годы ХХ века, советские ученые Б.Г. Ананьев, Л.У. Зонков, Д.Б. Эльконин и др. выделили научно-практическую проблему связи обучения и развития младших школьников. Было установлено, изменение содержания и методов традиционного начального обучения дает определенный положительный эффект в развитии детей. “Мы нашли ключ к проблеме развивающего обучения в младшем школьном возрасте, - писал Д.Б. Эльконин. - Этот ключ — содержание обучения. Когда мы хотим, чтобы обучение в начальных классах школы стало развивающим, то должны позаботиться о научности содержания. Это значит о том, чтобы дети усваивали систему научных понятий и способы их получения”.
В основу разработки новых систем начального обучения, которые ориентируются, прежде всего на развитие младших школьников, были положены следующие теоретические положения:
Ведущая роль в развитии принадлежит обучению.
Последователи научной школы Л.С. Выготского считают, что обучение может существенно влиять на развитие ребенка и поэтому должно идти впереди развития.
Обучение должно ориентироваться на зону ближайшего развития ребенка.
“То, что ребенок сегодня делает с помощью взрослого, завтра он может сделать самостоятельно. Зона ближайшего развития помогает нам определить завтрашний день ребенка, динамичный характер его развития, учитывая не только уже достигнутые, но и то, что находится в процессе созревания”, — писал Л.С. Выготский.
В основе обучения должен находиться активно-действенный способ (тип учения).
Идеи Л.С. Выготского о ведущей роли обучения конкретизировал П.Я. Гальперин, который доказал, что не всякое обучение оказывает существенное влияние на развитие. Он остановил, что успешность процесса усвоения знаний зависит от того, как организуется процесс ориентации ребенка в учебном материале. С точки зрения способа ориентировки и его полноты П.Я. Гальперин выделял три типа учения.
Первый тип.
Ориентировочная основа действия дается ученику в готовом виде в качестве образца с неполным набором ориентиров и указаний. Школьник, многократно выполняя аналогичные действия, путем проб и ошибок достигает необходимого результата. Процесс обучения при этом идёт стихийно.
Второй тип.
Ученику дается в готовом виде полная ориентировочная основа действия (программа выполнения формируемого действия по шагам — алгоритм) для выполнения отдельных конкретных практических задач. Система ориентиров помогает избежать ошибок, но не позволяет школьнику свободно оперировать полученными знаниями, так как для каждого следующего задания он ждет от учителя очередного готового образца выполнения действия.
Третий тип
. Ученик подводится к выяснению основных принципов работы с тем или иным учебным материалом. Учителю важно научить школьника как анализировать объекты, чтобы он смог самостоятельно устанавливать систему ориентиров, необходимых для правильного выполнения задания определенного типа. Ориентировочную основу своих действий школьник составляет сам. Обучение при этом с самого начала является полностью сознательным: ребенок не только понимает то, чему должен научится, но и владеет способом такого обучения. Овладение обобщенным способом действий позволяет ученику самостоятельно решать новые отдельные задачи. Именно такое обучение способно вести за собой развитие, потому что оно вооружает школьника методом нахождения основных специфических особенностей исследуемого предмета и позволяет в дальнейшем действовать самостоятельно.
Обучение должно опираться на закон развития от общего к частному, от целого к части.
Доктор психологических наук Н.А. Чуприкова в своей работе “Умственное развитие и обучение: психологические основы развивающего обучения” заметила: сущность закона заключается в том, что высокоразвитая система не складывается из отдельных элементов, а “дробится на элементы в процессе своего развития, расчленяется на все более и более мелкие части со все более и более специфической структурой и специализированными функциями” это значит развитие идет не от части к целому [11, 32]. Общее — это то исходное целое (клеточка), которое в процессе развития (через систему дифференциации) приводит к разным частным случаям своего проявления.
Я. Каменский в “Великой дидактике” более 300 лет назад писал о принципе природосообразности в обучении и воспитании, сравнивая природный ход развития познания ребенка с ростом и развитием дерева, которое берет свое начало с корня. Затем появляется ствол, а от ствола “все те главные веточки, которые у него потом должны быть, так что потом им приходится только разрастаться”. И чтобы вооружить человека на всю жизнь возможностями развивать свое познание, необходимо в первую очередь вырастить эти “главные веточки” его знаний и познавательных способностей [11, 35].
Умственное развитие ребенка определяется степенью развития внутренних когнитивных психологических структур, которые отвечают за глубокий и всесторонний анализ поступающей информации установление связи новых знаний с теми, что имеются в долгосрочной памяти, обеспечивают гибкость и подвижность мышления, возможность в любой момент использовать эти знания. В процессе обучения важно формировать на доступном ребенку уровне систему взаимосвязанных знаний, что создают внутренне упорядоченную структуру, а не просто сообщают некоторую сумму знаний.
Ребенок рассматривается как субъект всех видов деятельности,
свойственных младшему школьному возрасту, и в первую очередь учебной деятельности, которая является ведущей для данного возраста.
Придать обучению действительно развивающий характер, обеспечив условия для развития в младших школьниках воображения, рефлексного мышления, личностных действий и поступков, желания и умения учиться, возможно только через активное включение ребенка в учебный процесс. Школьник становится субъектом учебной деятельности на основе таких личностных самообразований, как активность, самостоятельность, умение вступать в отношения с другими людьми.
Целеустремленное формирование мотивационной основы учебной деятельности.
“Психологический закон утверждает: прежде чем предложишь ребенку какую-нибудь деятельность, постарайся заинтересовать его ею, позаботься про то, чтобы выяснить, что он готов к этой деятельности, что у него напряжены все силы, необходимые для нее, и что ребенок будет действовать сам, преподавателю же остается только управлять и направлять его деятельность”, — писал Л.С. Выготский [1, 118].
Организация учебного взаимодействия и сотрудничества в учебно-воспитательном процессе.
Согласно с Л.С. Выготским учитель может целеустремленно воспитывать детей только при постоянном сотрудничестве с ними, с их окружением, опираясь на желание и готовность учеников действовать вместе с педагогом. Эта фундаментальная идея противостоит требованиям авторитарной педагогики, согласно которой каждый учитель как будто может непосредственно эффективно воздействовать на ребенка, исходя из учебно-воспитательных целей, не учитывая мотивы, интересы и готовность ученика осуществлять собственную деятельность.
Обоснованием организации коллективно-поделенной учебной деятельности школьников с постепенным переходом на индивидуальное ее осуществление является фундаментальный закон развития психических функций человека, сформулированный Л.С. Выготским: “Всякая высшая психическая функция в развитии ребенка появляется на сцене дважды — сначала как деятельность коллективная, социальная, второй раз как деятельность индивидуальная, как внутренний способ мышления ребенка…”[1, 387]. Таким образом, организация учебных отношений и сотрудничества со взрослыми и товарищами является источником развития и существенным средством создания зоны ближайшего развития ребенка.
Опираясь на идеи Л.С. Выготского, А.М. Леонтьев, П.Я. Гольперин, А.У. Запорожец и др. обосновали понятие деятельности и субъекта. Огромное научное значение для развития начального обучения имеет теория, разработанная в 60-80-х годах большим коллективом психологов, методистов и учителей под руководством Д.Б. Эльконина и В.В. Давыдова.
Основами данной образовательной системы стали фундаментальные теории периодизации психического развития в детском возрасте (Д.Б. Эльконин), двух типов обобщения и мышления (В.В. Давыдов), учебной деятельности как субъекта (Д.Б. Эльконин, В.В. Давыдов, Г.А. Цукерман), развивающего обучения.
Целенаправленное формирование учебной деятельности школьников является главной определяющей чертой этой системы. Другие системы не связывают понятие “развивающее обучение” с понятием “учебная деятельность” и строятся на других основах.
Система развивающего обучения не противопоставляет себя обычному обучению: любое обучение в той или иной степени способствует развитию мышления ребенка, становлению его личности. Данную систему необходимо рассматривать не как развивающее обучение вообще, а как такой тип обучения, который способствует в первую очередь развитию у младших школьников основ теоретического мышления, это значит способности понимать сущность явлений по их внешней форме и действовать соответствующим образом. Развивающее обучение по определению В.В. Давыдова, направлено на формирование у детей основ теоретического мышления, или, более широко, основ теоретической сознательности, к определяющим формам которой вместе с наукой относятся искусство, мораль, право, религия и политика.
В.В. Давыдов видел решение проблемы гуманизации начального обучения в создании условий для становления младшего школьника как субъекта собственной деятельности и в использовании такого содержания и таких методов обучения, которые способны обеспечить существенное психическое развитие ребенка и сформировать у него учебные умения, необходимые для дальнейшего образования.
Специфику образовательной системы Д.Б. Эльконина — В.В. Давыдова можно представить в виде схемы, которая отображает единство содержания, методов и форм обучения.

Содержание развивающего обучения
: являются теоретические знания, которые представлены системой понятий о данной ветви реальности вместе со способом действий, с помощью которых понятия и их система формируются у учеников. Понятие знание существенных отношений между отдельными сторонами предмета или явления. Поэтому для формирования понятия необходимо в первую очередь выделить данные стороны, а для этого выполнить определенные действия с предметами, чтоб свойства проявились.
Учебный курс начинается с изучения фундаментального обобщенного понятия, которое постепенно обогащается и конкретизируется отдельными фактами и знаниями, служит для учеников ориентиром и помогает осмыслить все частные случаи, которые вводятся в дальнейшем. В результате осуществляется постепенное движение от общего к частному, от абстрактного к конкретному.
Усвоение теоретических знаний осуществляется в процессе учебной деятельности. При этом возникают и развиваются такие новообразования, как содержательная рефлексия, анализ и планирование [5, 383]. Эти новообразования определяют важное перестроение осей познавательной и личностной сфер деятельности детей и являются основой психического развития младших школьников. Обеспечить качественное усвоение детьми достаточно сложной системы понятий с опорой на учебную активность репродуктивного типа заведомо невозможно. Поэтому организация полноценной учебной деятельности школьников является главным и существенным условием, которое обеспечивает их развитие в процессе обучения.
Учебная деятельность
— особая деятельность учеников, которая сознательно направлена на усвоение знаний [9,478]. Надо учитывать, что усвоение новых знаний может осуществляться без целенаправленной учебной деятельности школьников в процессе игры, трудовой деятельности, во время занятий спортом. При этом не ставится цель получить знания: ребенок играет ради игры, занимается спортом для развития своих физических качеств. Поэтому с психологической точки зрения, полученные знания являются побочным продуктом указанных видов деятельности. Только в учебной деятельности получение новых знаний рассматривается как главная цель.
С.Л. Рубинштейн в связи с этим говорил, что существуют “два вида деятельности, в результате которых человек овладевает новыми знаниями и умениями. Один из них специально направлен на овладение этими знаниями и умениями, как на свою непосредственную цель. Второй приводит к овладению этими знаниями и умениями, осуществляя иные цели. Учение в последнем случае — не самостоятельная деятельность, а процесс, что осуществляется как компонент и результат деятельности, в которую он включен”[7,76].
Ключевое слово “деятельность” имеет целью творческое превращение школьниками учебного материала, это значит такое его изучение, при котором выясняются происхождение, становление и развитие предмета или явления. Поэтому учебной деятельностью нельзя считать усвоение детьми знаний, которые им представляются учителем в готовом виде.
Важным этапом процесса организации учебной деятельности является постановка учебной задачи, когда дети убеждаются, что способов действия, которыми они владеют, недостаточно для решения новой задачи. В этот момент учитель не дает ученикам никаких определенных образцов, готовых способов решения, которые можно восстановить, а организует поиск способов действия, которых не хватает.
Учебной называется такая задача, которая заставляет школьника искать общий способ решения всех задач данного типа. Учебная задача может ставиться только в отношении к какому-нибудь фундаментально значимому понятию, что открывает весь учебный предмет или крупный раздел учебного курса [6, 66].
Осуществляя учебную деятельность школьники выполняют определенные учебные действия. В.В. Давыдов представляет их в логике решения учебной задачи:
принятие от учителя учебной задачи или ее совместная постановка;
превращение условий задачи с целью выявления всеобщих отношений изучаемого объекта (поиск, нахождение и выделение);
моделирование выделенных отношений в предметной, графической или буквенной форме;
превращение модели отношений для изучения их особенностей в “чистом виде”;
построение системы отдельных задач, которые решаются общим способом;
контроль за выполнением предыдущих действий;
оценка усвоения общего способа как результата решения данной учебной задачи [5, 159 — 160].
Учитель в процессе обучения целенаправленно и последовательно ведет детей от одной учебной задачи к другой. За решением одной задачи идет постановка следующей. Отрезок времени от постановки одной “стратегической” задачи к другой через выполнение промежуточных “тактичных” задач А.Б. Воронцов называет актом учебной деятельности[2, 212 — 214].
Когда учитель освоил технологию организации полного акта учебной деятельности и в соответствии с ним организует полноценную учебную деятельность школьников, то можно говорить, что он овладел технологией развивающего обучения
.
Центром учебной деятельности является субъект. Позиция субъекта характеризуется самостоятельным осуществлением всех этапов деятельности: постановки цели, планирования, реализации цели и анализа полученных результатов. Младший школьник как субъект осуществляет собственную учебную деятельность вместе с другими детьми и с помощью учителя. Возникновение у школьника потребности в учебной деятельности, возникновение мотивов учебных действий способствует формированию у него желания учиться. Овладение учебными действиями с помощью которых решаются учебные задачи, формирует у ребенка умение учиться. Именно желание и умение учиться характеризуют младшего школьника как субъекта учебной деятельности. При этом от овладевает такими важными личностными качествами, как самостоятельность, инициативность, ответственность.
Изучение алгебраического материала начинается с подготовительного класса и проходит в тесной связи с изучением арифметического и геометрического материала.
Учащиеся начальных классов знакомятся с такими важнейшими понятиями как равенство, неравенство, уравнение.
Что же такое равенство, неравенство, уравнение?
Пусть а и в — числовые выражения. Числовые выражения или числа, между которыми стоит знак равенства, называются числовыми равенствами.
Неравенство — отношение, связывающее два числовые выражения или два числа посредством одного из знаков ”>” (больше), ”<” (меньше), ”³” (больше или равно), ”£” (меньше или равно), ”¹” (не равно).
Равенство с переменной f(х) = g(х) называется уравнением с одной переменной.
Переходим к краткому обзору методики ознакомления с числовыми равенствами, неравенствами, уравнениями в традиционной школе.
Понятия о равенствах, неравенствах, уравнениях раскрываются во взаимосвязи.
Числовые равенства и неравенства изучаются параллельно. Упражнения с равенствами и неравенствами используются для раскрытия и применения арифметических знаний, а также для выработки вычислительных навыков.
Ознакомление с равенствами и неравенствами в традиционной школе непосредственно связывается с изучением нумерации и арифметических действий и происходит в несколько этапов.
2.1. Непосредственное сравнивание предметов
На подготовительном этапе в дочисловой период, нужно в процессе практических упражнений с использованием пар понятий научить детей сравнивать предметы и устанавливать отношение “больше”, “меньше”, “одинаково”. Приведем примеры наиболее распространенных пар понятий: больше-меньше, выше-ниже, шире-уже, правее-левее, старше-моложе, тяжелее-легче, толще-тоньше, дальше-ближе, быстрее-медленнее.
С первых же уроков отрабатывается умение сравнивать численности множеств. При этом начинать нужно с упражнений на установление между множествами взаимно однозначного соответствия.
Основой таких упражнений могут служить различные ситуации из обыденной жизни: каждому ученику в классе взаимно однозначно соответствует его ранец; каждой чашке в чайном приборе однозначно отвечает блюдце, на которое ставят чашку.
Предлагая учащимся упражнения на сравнение численности множеств, целесообразно начинать с множеств, каждое из которых составлено из однородных предметов, например, одно множество состоит из треугольников, другое — из квадратов. Через некоторое время переходят к сравнению множеств разнородных предметов.
Полезно ознакомить учащихся с различными приемами попарного соотнесения предметов двух множеств. Первым приемом будет являться наложение предметов на наборном полотне друг на друга. Второй прием — изымание по одному предмету из каждого множества и откладывание полученных пар. Третий прием — сравнение двух множеств, элементы которых нельзя изымать, например, множеств предметов, изображенных на рисунке. Четвертый прием целесообразно применять для сравнения двух множеств, нарисованных предметов, если эти предметы не расположены линейно. Такое сравнение предметов “один к одному” дает возможность устанавливать не только, где больше, а где меньше, но и на сколько больше, на сколько меньше. Уже в подготовительный период включают упражнения на преобразование неравночисленных множеств в равночисленные и обратно.
Таким образом происходит непосредственный способ сравнения предметов в традиционной школе.
Система РО
. Необходимость сравнения по какому-либо признаку возникает в ситуации восстановления какого-либо объекта, обладающего изучаемыми свойствами.
Именно задача восстановления (а затем и воспроизведения) вынуждает ребенка выделить свойства предметов и сконструировать способы их сравнения по выделенному признаку.
Сначала ребенок выполняет практическое действие сравнения различных реальных предметов, которые можно взять в руки. В школе дети должны работать не с рисунками, а с реальными предметами. Желательно, чтобы каждый ребенок имел возможность работать с предметным материалом. Если такой возможности нет, и учитель использует демонстрационные пособия, то с ним работает не учитель, а дети (по очереди выходя к доске), с их помощью показывая, как они мыслят.
Затем ребенок сравнивает объекты, которые нельзя взять в руки.
Каким же образом это происходит?
а) выделяются те признаки предмета, по которым его можно сравнивать с другими;
б) находят разные способы сравнения предметов, например, при сравнении по длине дети опираются на зрительное восприятие, т.е. первоначально сравнивают “на глаз”, а затем, когда этот способ не срабатывает, находят другие способы (наложение, приложение).
Научившись сравнивать предметы (полоски, стороны геометрических фигур или тел и др.) по длине, ширине и высоте, ребенок попадает в ситуацию, когда этого его умения станет недостаточно для сравнения. Например, когда вместо привычных полосок — прямоугольников он сталкивается с кругом, у которого ребенок не может обнаружить ставшие привычными длину и ширину, тогда он стоит перед необходимостью сравнения по другому признаку — площади.
Такой общий подход к появлению новых признаков сравнения предметов позволяет ребенку уже на первых этапах обучения использовать его при решении целого класса частных задач на сравнение, что в свою очередь, значительно расширяет набор признаков, по которым можно сравнивать предметы. Например не только по длине (ширине, высоте), площади, объему, массе, форме, цвету, материалу, количеству, но и по углам, расположению на плоскости и в пространстве, по составу частей и даже по “красоте”. Сравнение по “красоте” является ключом к формированию каллиграфического навыка.
Таким образом, действуя с реальными предметами, их признаками и результатами сравнения по заданному признаку, дети выделяют существенные связи и отношения между компонентами действия выполняя три основных типа заданий:
а) есть предметы, известен признак — необходимо установить результат сравнения;
б) есть предметы, известен результат сравнения — нужно установить, какой признак был выбран;
в) известны признак и результат сравнения — подобрать соответствующие предметы.
Вариативность этих заданий очевидна, что позволяет в полном объеме контролировать свои действия и по мере необходимости их перестраивать.
Сравнивая предметы по тому или иному признаку, дети устанавливают отношение равенства или неравенства (на первых порах фиксируя результат сравнения с помощью слов: “они одинаковые”, “равные”, “их столько же” или “они неодинаковые, разные, неравные” и т.д.).
Необходимо заметить, что чем больше слов-синонимов для описания отношений равенства и неравенства будет использовать учитель, тем легче будет детям “переводить” тексты арифметических задач на язык математики. Для введения сравнения групп предметов сначала необходимо ввести понятие комплекта, включающего составные части, а затем научиться сравнивать комплекты по составу частей. При сравнении комплектов по составу (набору) частей будет иметь значение не цвет, не размер частей, а только их набор. Это даст возможность сравнивать разные группы предметов по отношению к определенному комплекту, включающему тот или иной набор частей.
2.2. Моделирование отношений равенства и неравенства:
предметное
: с помощью полоски
графическое
:
а) с помощью копирующего рисунка;
б) с помощью отрезков (схемы).
О введении графической схемы хотелось бы рассказать поподробнее.
Для подведения детей к использованию графической модели необходимо задать конкретно-практическую задачу. Вы показываете детям две разные по объему “фигуристые” банки или бутылки и просите детей с помощью рисунка показать, что объем одной банки больше объема другой. Опыт показывает, что дети начинают рисовать форму банок, т.е. делают копирующий рисунок. Тогда вы подходите к детям и начинаете “придираться”: то форма не такая, то горлышко слишком узкое и т.д., т.е. должны осознать бессмысленность такого изображения (копирующего рисунка), тем более, что банки при сравнении по объему можно использовать разные по форме, но одинаковые по объему.
А потом начинается диалог:
Учитель: — Что вы хотели сообщить рисунком?
Дети: — В каком отношении находятся объемы банок.
Учитель: — А как мы сообщаем о результатах сравнения?
Дети: — С помощью длин полосок.
Учитель: — Попробуйте нарисовать, в каком же отношении находятся объемы банок.
Если дети нарисовали полоски, то можно продолжать разговор дальше. Если снова стали рисовать банки, нужно дать время для обсуждения в группах и прийти к выводу о неудачности такого способа.
Учитель: — Нужно ли рисовать форму банок или легче нарисовать полоски?
Дети: — Легче нарисовать полоски.
Учитель: — Нарисуйте.
Окажется, что разные дети нарисовали полоски, разные по длине, ширине.
Учитель: “Какой же длины и ширины можно рисовать полоски?” Обсуждая этот вопрос, дети придут к выводу, что полоски должны быть одинаковыми или разными по длине в зависимости от результата сравнения, а вот ширина полоски значения не имеет.
Учитель: — Если ширина может быть любой, то полоску какой ширины мы будем рисовать?
Для осознания того, что ширину полоски можно совсем не рисовать, можно предложить детям такое задание: “По моей команде изобразите в тетради результат сравнения площадей фигур” (они должны быть равны). После выполнения задания темой обсуждения должна стать скорость выполнения: почему одни нарисовали быстрее, а другие медленнее. В результате вы приходите к выводу, что удобнее ширину вообще не рисовать, а изображать только длину полоски. Если величины (длина, площадь, объем) оказались одинаковыми, то изображают равные по длине отрезки, а если неодинаковыми, то и отрезки неодинаковые. Таким образом вводится изображение величин с помощью отрезков.
Дети, без сомнения, смогут научить этому других, показывая, как изобразить два равных или неравных по длине отрезка. Очень важно, чтобы ребенок осознал сам способ изображения, при котором отрезки должны быть фактически параллельными и один конец должен при мысленном наложении совпадать с другим.
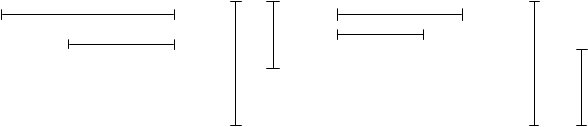 |
Конечно, дети найдут свои слова при объяснении способа. Важно понимать, что, в отличие от традиционного подхода, при котором дети сначала рассказывают, как нужно делать, а лишь затем начинают действовать. В РО все с точность до наоборот — сначала ребенок выполняет практическое действие, а лишь затем “учит” других делать так, как умеет делать сам, т.е. объясняет, как нужно действовать, что эффективно развивает речь ребенка. Ведь для объяснения другому человеку нужно будет подобрать, найти такие слова, которые были бы ему понятны. Отсюда следует, что задача учителя — внимательно слушать ребенка, играя роль непонимающего человека для того, чтобы действовать в соответствии с объяснением ребенка. Тогда и будет понятно, насколько осмысленно выполняет ребенок практическое действие.
Теперь можно предлагать детям для решения три обратные задания:
Даны предметы и величина. Нужно построить схему;
Даны схема и предметы. Надо узнать величину;
Даны схема и величина. Нужно подобрать предметы.
При обсуждении с детьми результатов сравнения можно предложить детям придумать задания с “ловушками”: с длиной — взять две одинаковые по длине нитки, которым придать разную форму; площадью — взять два одинаковых прямоугольника, один из них разрезать и превратить в квадрат и т.д.
Подведем итоги наших рассуждений. Сначала ребенок осуществляет практическое действие с предметами, которое назовем предметным действием, от которого ребенок с опорой сначала на копирующий рисунок, а затем на предметную модель переходит к графической модели, а от нее после введения математических знаков и букв для обозначения величин он перейдет к описанию этих действий с помощью формулы, т.е. к буквенно-знаковой модели, а затем (значительно позже) к словесным моделям (правилам, определениям). Смотреть приложение 1.
знаковое
:
а) с помощью знаков “=” и “¹”
б) с помощью букв и знаков “=”, “>”, “<”, (формулы)
Основная задача при введении буквенного обозначения состоит в том, чтобы помочь ребенку мысленно отделить свойство предмета от самого предмета. Выделенной в результате сравнения отношение равенства или неравенства должно быть обобщено в формуле, т.е. в буквенно-знаковой записи.
Удобнее вводить буквенные обозначения, используя предметы, которые можно сравнить по длине, ширине, площади и объему.
Для постановки конкретно-практической задачи ставим детям два сосуда, которые должны быть одинаковыми по объему, разными по высоте и площади основания, и просите сравнить их по какому либо признаку, изобразив результат сравнения с помощью схемы. В каждой группе должны быть одинаковые пары баночек. Раздав баночки вы быстро проходите по классу и шепотом договариваетесь с группами, по какому признаку они будут сравнивать.
При сравнении у разных групп получаются разные схемы (если работало больше трех групп, не забудьте перед началом обсуждения выяснить с ребятами, у каких групп получились одинаковые схемы, и рассматривать схемы по данному признаку).
Возникает проблема. Как такое могло произойти? Почему это могло произойти? Нужно дать детям возможность обсудить этот вопрос. Обязательно найдутся ребята, которые скажут, что разные группы сравнивали по разным признакам, и даже какая схема сообщает о сравнении по высоте, какая — по объему, а какая — по площади донышек. Тогда возникает вопрос: чем дополнить схему, чтобы другим людям было понятно, по каким признакам мы сравнивали эти сосуды, когда строили каждую из схем?
Возникает потребность в буквенном обозначении признака, а не предмета.
Предлагаем детям подумать, как на схеме показать, по какому признаку сравнили предмет. Кто-то нарисует рядом со схемой предметы, кто-то напишет словом, кто-то воспользуется первой буквой слова — названия признака. После обсуждения всех предложений вы придете к выводу, что удобнее обозначать одной буквой, а затем познакомите ребят с буквами латинского алфавита, которые используют для обозначения. Дети дополняют свои схемы буквами и записывают с вашей помощью формулу. Используя вопросы, подводим детей к необходимости введения знаков “<”, “>”.
Далее предлагаем обратные задачи:
на восстановление предметов по схеме и формуле;
на восстановление предметов и схеме по формуле;
на восстановление предметов и формулы по схеме;
на восстановление схемы и формулы при сравнении предметов по определенному признаку.
В традиционной школе преобладает знаковое моделирование — вводятся знаки отношений “>”, “<”, “=”.
Первые числовые равенства, с которыми знакомятся дети, образованы при ознакомлении с действиями сложения, вычитания в концентре “Десяток”.
Введение знака “<” можно осуществить, выполняя такое упражнение. Учитель на доске, а учащиеся в тетрадках рисуют один предмет, например квадрат (закрашивают одну клеточку). Отступив немного (три клетки) вправо, рисуют два квадрата. Ученики делают вывод, что слева квадратов меньше, чем справа. Под одним квадратом пишут цифру 1, а под двумя — цифру 2, произносят: “Число 1 меньше числа 2” и между написанными цифрами 1 и 2 ставят знак “<”. Подобным образом вводятся записи вида 1=1, 2>1.
Чтобы учащиеся не путали знаки “<” и “>”, полезно воспользоваться мнемоническим приемом: где палочки расходятся, записывают большее число, а где сходятся — меньшее число.
2.3. Подбор величин по формулам равенства и неравенства
Основная задача данного этапа работы заключается в том, чтобы помочь ребенку осмыслить способы математического описания отношений между величинами с помощью схемы и формулы, а также восстановления величин, т.е. подбора предметов — носителей величины — по схеме или формуле. Это значит, что рассматриваются задания трех основных типов:
1) Даны предметы. Сравнивая по тому или иному признаку, дети чертят схему, показывающую отношение между величинами, а затем описывают это отношение в знаковой форме:
 А А А А А А
В В В
А>B или В<А А=В или В=А А<B или В>А
Важно, чтобы дети понимали, буквами А и В могут быть обозначены любые величины: длина (высота, ширина, толщина, глубина, периметр, и т.д.), площадь, масса, объем, количество, величина угла, а об отношении между ними можно сообщить словами: больше-меньше, выше-ниже, шире-уже, правее-левее, старше-моложе, тяжелее-легче, толще-тоньше и т.д. В математике все эти отношения описываются понятиями “больше-меньше”. Отношение “равно-неравно” может быть в быту описано словами “столько же”, “такие же”, “одинаковые”, “разные” и др., употребляя которые ребенок должен понимать, о какой величине идет речь. Так, например, когда говорят: “Купили 6 таких же стульев”, имеют в виду не их расцветку или форму, а как правило, цену, по которой приобрели эти стулья. Или в задаче сказано: “Если сшили 8 таких же платьев”, то речь идет опять же не о фасоне или расцветке ткани, а о расходе ткани на одно платье, и т.д.
2) Дана схема, описывающая отношение между величинами, нужно подобрать соответствующие величины (т.е. предметы-носители этих величин) и записать формулу.
3) Дана формула, описывающая отношение между величинами, нужно построить схему и подобрать соответствующие величины.
Отбирая материал к уроку, нельзя использовать однотипные упражнения, как это принято в традиционной школе, для закрепления и формирования навыка. В данной системе обучения, одной из задач которой является развитие и формирование способности думать, рассуждать, мыслить, нужно для уроков подбирать задания разного типа из разных блоков, что дает ребенку возможность осмысливать изменение условий, влекущее за собой изменение способа действия, и устанавливать различные связи и отношения как между величинами, включенными в задание, так и между заданиями. Это позволит в дальнейшем осознать принцип, который положен в основу придумывания заданий по типу составления “обратных” задач, когда меняются “ролями” известные и неизвестные величины.
Для выполнения каждого из данных типов заданий хорошо использовать группу из 3-4 детей: один действует с предметами, молча демонстрируя способ их сравнения, другой описывает результат сравнения с помощью схемы, третий на основании либо схемы, либо увиденного способа сравнения величин обозначает их буквами и записывает формулу (равенства или неравенства), используя знаки “=”, “>” и “<”, а четвертый выступает контролером, при этом разные группы могут работать с разными величинами.
Обсуждение итогов работы каждой группы может происходить следующим образом: каждая группа называет величину, с которой она работала. Остальные дети по схеме и формуле определяют, какие предметы могла сравнивать группа и какие ошибки при сравнении, при составлении схемы или записи формулы она могла допустить.
После такой проверки можно предложить группам, парам или отдельным детям (по выбору) придумать свои задания на сравнение или восстановление величин (с которой она работала) по схеме и формуле. Придумав задание, каждый должен выполнить свое задание так, как он хотел бы, чтобы его выполнили другие, а затем организовать “аукцион” заданий, при котором каждый выбирает понравившееся ему (из придуманных детьми) задание.
Предложенные задания можно классифицировать и по другому основанию: большинство из перечисленных заданий позволяет детям познакомиться с основными свойствами равенства и неравенств, однако названий рассматриваемых свойств детям сообщать не нужно. Главное, что дети должны понять, что иногда непосредственного сравнения величин производить не нужно, чтобы узнать, в каком отношении они находятся, т.е. вывод можно сделать, опираясь на результаты сравнения этих величин с другими.
Так, если А=В, то В=А (свойство симметричности), т.е. А сравнили с В, то нет необходимости вновь брать в руки предметы, чтобы сравнивать В и А. Если же А=В, а В=С, то нет необходимости А и С сравнивать непосредственно, так как А наверняка будет равно С, — это свойство транзитивности равенства. Аналогично можно рассмотреть транзитивность неравенства: если А>В, а В>С, то А>С, и если А<В, а В<С, то А<С.
Тот факт, что буквой может быть обозначена любая величина, дает возможность приступить к использованию дошкольного опыта ребенка, а именно: после составления одной из формулы А>В или А<В предлагать детям подбирать вместо букв подходящие числа. Здесь слово “подходящие” относится как к самому отношению (больше или меньше), так и к дошкольному опыту ребенка, что дает возможность каждому ребенку продемонстрировать свою дошкольную подготовку и при этом быть успешным при любом объеме дошкольных умений.
Переход от букв к подходящим числам дает возможность и для обратных действий, при которых дети восстанавливают буквенные формулы с помощью числовых. Этот обратный переход можно задать следующим образом: “Дети в другом классе вместо букв в формуле подобрали подходящие числа. Вот что они записали: 7<8. Как вы думаете, какая была формула?” Дайте возможность обсудить это в группах.
В дополнение к указанным заданиям необходимо предложить выполнить задание с “ловушкой”:
- поставить двое весов: на одни весы положить одинаковые по массе предметы и на другие тоже. Записать либо М1
=М2
и М3
=М4
, либо А=В и С=Д.
Возникает вопрос: можно ли, не взвешивая самих предметов, сравнить массы А и Д (а следовательно, и В и Д, А и С, В и С)? Если ребенок понимает свойство транзитивности, то он должен утверждать, что такого сравнения без взвешивания сделать нельзя, массы А и Д могут оказаться как одинаковыми, так и разными.
Если ребенок обращает внимание только на знаки равенства, а связи между сравниваемыми величинами не видит, то его вывод будет неверным, т.е. он будет утверждать: А=Д. Тогда и возникает вопрос: как не ошибиться? Для этого следует сделать две записи и сравнить их.
I II
А=В, а В=Д А=В, а С=Д
Сравнить
А и Д А и Д
Первая позволяет без непосредственного сравнивания сделать вывод А=Д, а вторая нет: может оказаться А>Д, А<Д, А=Д, все будет зависеть именно от отношения между А и С.
Схема даст возможность обосновать свою точку зрения, а затем вновь вернуться к равенствам, по которым можно определить, во-первых, сколько величин участвует в сравнении и, во вторых, как связаны эти величины между собой. Могут появиться следующие записи и схемы (см. приложение ).
Важно помнить, что обсуждение данного материала следует начинать не до того, как дети собираются чертить схемы, а после того, как схемы к формулам готовы.
Традиционно же все делается наоборот: сначала дети говорят, обсуждают, как выполнять задание, а потом его делают, а в этой системе обучения нужно сначала сделать (осуществить практическое действие), а затем обсуждать, как это сделали и как научить других делать то, что умеешь делать сам. Повторю, это коренное и принципиальное отличие подхода к обучению в системе РО.
Итогом работы над данной темой является составление справочника ошибок, в который как раз включаются все возможные ошибки, которые были или могут быть (!) у детей. Фиксируя их в справочнике любым удобным для детей способом, необходимо каждый раз возвращаться к вопросам о происхождении этих ошибок, а также к способам их обнаружения и исправления, что является необходимым этапом дальнейшего предупреждения этих ошибо
к.
2.4. Переход от неравенства к равенству и наоборот
Основная задача в том, чтобы дети смогли найти три способа уравнивания:
1) путем увеличения одной (меньшей) величины до ее равенства с другой (большей), т.е. с помощью сложения:
А А
В После уравнивания В С
А>В А = В + С
2) путем уменьшения одной (большей) до ее равенства с другой меньшей, т.е. с помощью вычитания:
А А
В После уравнивания В В С
А>В А – С = В
   3) путем уменьшения одной и увеличения другой на одну и ту же величину: 3) путем уменьшения одной и увеличения другой на одну и ту же величину:
     А А А А
ВПосле уравнивания С С К
А>В В К
А – К = В + К
Третий способ предполагает свободное владение первыми двумя.
Итак, два первых способа уравнивания величин являются основными.
Постановку задачи, требующей уравнивания величин, начнем со сказочного сюжета о Незнайке.
Прочитайте ту часть сказки, в которой рассказывается о том, как Винтик и Шпунтик изобрели автомобиль, который работал на газированной воде с сиропом (текст приведен в учебнике).
Результатом обсуждения возможных причин остановки машины станет постановка задачи, требующей уравнивания величин.
Нужно в бак налить столько сиропа, сколько его не хватает, чтобы бак стал полным.
Налейте воды (подкрашенной!) в две банки так, чтобы одна из них была полная (но не до самого края, чтобы можно было при необходимости долить немного воды), а вторая заполнена примерно на 1/3. Объясните, сколько сиропа должно быть и сколько осталось. Условие работы “двигателя” – полная банка.
Теперь вместе с детьми переведем эту задачу на язык математики:
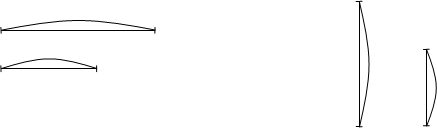 Есть две неравные величины (объем воды в банках). Изобразим их, обозначив буквами (например А и В), и запишем формулу: Есть две неравные величины (объем воды в банках). Изобразим их, обозначив буквами (например А и В), и запишем формулу:
А
В
или А
А>В В
В сюжетной задаче о баке нам нужно узнать, сколько сиропа нужно добавить в неполную банку, чтобы машина снова могла ехать. Эта же проблема на языке математики выглядит так: нужно уровнять величины так, чтобы меньшая величина В стала равна большей величине А.
Как это можно сделать?
Сначала дети выполняют практическое действие, пытаясь в неполную банку долить воды до того же уровня, что и в первой банке, т.е. долить воды столько, сколько ее не хватало до полной банки. Проще говоря, проблема сначала выглядит так: что нужно сделать, чтобы в неполной банке воды стало столько же, сколько в полной банке? Ответ не заставит себя ждать, и дети тут же скажут, что воду нужно долить. Вы непременно выполняете практическое действие, доливая воды значительно меньше, чем нужно (или, наоборот, больше).
Если дети скажут, что этого мало, то долейте заметно больше, чем нужно (или отлейте больше, чем нужно). Именно тогда дети и смогут осмыслить то, что речь идет об определенном количестве – ни больше, ни меньше.
Возникает новая задача: какое количество воды нужно долить, чтобы стало поровну?
Невозможность восстановить прежний объем есть основание для рождения у детей о метках на обеих банках.
Поскольку дети уже умеют изображать величины, то предложите им сначала изобразить данные величины (объемы воды или количество воды) с помощью схемы, обозначив их буквами.
Затем, запишем формулы: А>B или B<A.
Теперь ответ на вопрос (сколько же нужно долить воды?) может быть показан на банках и на схеме: 1) на банках: от метки на одной банке до метки на другой или с помощью двух меток на одной банке, если вторая метка прикреплена детьми при сравнении:
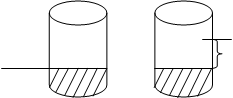
Метка, которую добавили
Метка дети, на том же уровне, что
и на первой банке
На схеме эту же разность (разницу) дети могут показать так:
это тот объем воды, который нужно долить
А в банку с меньшим объемом (В).
Помните! Не банка В, а объем воды
В в банке – это В, банки то одинаковые.
Показать то, сколько нужно долить воды, – это то же самое, что узнать, на сколько одна величина больше другой или меньше другой, – А>В (на С). Чтобы узнать эту новую величину С, нужно от большей величины отнять меньшую, т.е. С = А – В.
Значит, если к величине В добавить разницу, а “настоящие математики” говорят “разность”, – величину С, равную А – В, то получится величина, равная А.
 А = В + С (1) или А = В + (А – В) (2) А = В + С (1) или А = В + (А – В) (2)
С
Найти эту разницу, т.е. разность между величинами и записать формулу (2) дети смогут лишь после введения знака “минус”.
Чтобы изменить отношение между величинами, т.е. из неравенства сделать равенство или, наоборот, из равенства сделать неравенство (но таких заданий мало, т.к. они являются обратными, восстанавливающими неравные величины из равных, поэтому их желательно дополнить), нужно будет одну из двух величин либо увеличить (+), либо уменьшить (–), а может быть уменьшить одну и увеличить другую, причем на сколько уменьшают одну, на столько же увеличивают другую.
Очень важно, чтобы дети понимали: когда они от неравенства переходят к равенству, то отнимать или добавлять нужно не сколько угодно, а определенное количество, соответствующее разности этих величин.
Работа с графическими и знаковыми моделями, т.е. схемой и формулой, является основным звеном в цепи решения учебной задачи.
Отношение неравенства однородных величин (А<В) и операция сложения (А+В=С) обладают следующими свойствами:
Каковы бы ни были А и В, имеет место одно и только одно из трех отношений: или А=В, или А<В, или В<А.
Если А<В и В<С, то А<С (транзитивность отношений “меньше”, “больше”).
Для любых двух величин А и В существует однозначно определенная величина С=А+В.
А+В = В+А (коммуникативность сложения).
А+(В+С) = (А+В)+С (ассоциативность сложения).
А+В >А (монотонность сложения).
Если А>В, то существует одна и только одна величина С, для которой В+С=А (возможность вычитания).
Изучение свойств отношений, о которых шла речь, открывает перед ребенком новые возможности.
2.5. Как из частей составить целое
Система РО.
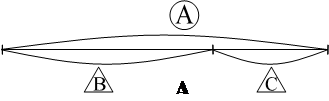
Введение об отношении частей и целого понятия обусловлено, прежде всего необходимостью обучения ребенка решению текстовых задач (прямых и косвенных) алгебраическим способом, т.е. на основе составления уравнений. Для этого ребенок должен научится изображать это отношение с помощью схем, опираясь на которые он сможет описать это особое отношение величин, не зависящее от их конкретного числового значения, в виде буквенных формул. Сформировав это понятие, дети приобретают умение выражать целое через части и части через целое:
И , где
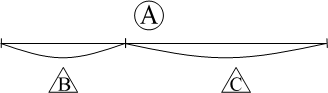 кружками обозначено целое, а треугольником – части. Графической моделью этого отношения могут служить разные геометрические фигуры (круг, прямоугольник, треугольник и др.), но наиболее удобным и простым способом изображения этого отношения является отрезок. кружками обозначено целое, а треугольником – части. Графической моделью этого отношения могут служить разные геометрические фигуры (круг, прямоугольник, треугольник и др.), но наиболее удобным и простым способом изображения этого отношения является отрезок.
Рассматривается и буквенно-графическая модель:
всем хорошо знакомые “лучики”, используемые традиционной школой для изображения состава числа.
 Введение знаков для обозначения целого и частей дает ребенку возможность относительность этих понятий. Во-первых, дети должны понять, что пока над величиной не производишь никакого действия – нельзя установить, является она (величина) частью или целым, т.е. одна и та же величина может быть частью по отношению к одной величине и она же является целым по отношению к другой. Введение знаков для обозначения целого и частей дает ребенку возможность относительность этих понятий. Во-первых, дети должны понять, что пока над величиной не производишь никакого действия – нельзя установить, является она (величина) частью или целым, т.е. одна и та же величина может быть частью по отношению к одной величине и она же является целым по отношению к другой.
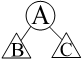 Например: Например:
Теперь величину В разобьем еще на 2 части К и Д, по отношению к которым В – целое.
  Величина В по отношению к А является частью, а по отношению к величинам К и Д является целым. Наложение знаков и , друг на друга позволяет лучше увидеть относительность этого понятия. Величина В по отношению к А является частью, а по отношению к величинам К и Д является целым. Наложение знаков и , друг на друга позволяет лучше увидеть относительность этого понятия.
Итак, понятие “целое” и “часть” – это относительные понятия; основное свойство этого отношения: целое не может быть меньше части, или часть не может быть больше целого. Сравнивать части между целым и остальными частями.
Умение изображать графически и описывать с помощью формул отношение частей и целого даст возможность решать целый класс текстовых задач с буквенными данными путем составления уравнений. Решив таким образом задачу, ребенок вместо букв подбирает подходящие числа и тем самым осознает, какова область допустимых значений букв не только по отношению к выполнимости арифметического действия, но и по отношению к реальности сюжета и к собственному опыту оперирования с числом. Такой подход позволяет учителю обнаружить “слабые” места у детей и незамедлительно приступить к коррекции.
Если же задача предложена с числовыми данными, то прежде чем ее решать, необходимо “восстановить”, какой она могла быть до того, как вместо букв дети из другого класса (или автор учебника) подобрали (придумали), как им кажется, подходящие числа. Это значит, что, прежде чем приступить к решению задачи, нужно установить, говоря языком математики, входят ли числовые данные в область допустимых значений по отношению к реальности сюжета. Другими словами, дети должны оценить, соответствуют ли данные числа смыслу задачи, ее сюжету, а затем заменить числа буквами и, решив задачу, вместо букв данные числа. Восстановление исходной (буквенной формы задания) текстовой задачи ставит перед детьми новую проблему: заменять одинаковые числа одинаковыми буквами или разными? Ответ на такой вопрос с неизбежностью потребует более глубокого осмысления текста задачи и тех понятий, которые составляют ее смысл.
С помощью заданий в разделе “Проверь себя!” вы сможете составить сначала проверочную работу, а затем и контрольную (контрольная работа по данной теме подводится не сразу по завершении ее изучения, а после рассмотрения следующей!)
2.6. Что такое уравнение
?
Система РО.
Описание методики работы над построением и решением уравнений рассмотрим с рассмотрения различных определений уравнения.
В школьной энциклопедии уравнение определено как “два выражения, соединенные знаком равенства; в эти выражения входят одна или несколько переменных, называемых неизвестным. Решить уравнение – значит найти все те значения неизвестных (корни или решения уравнения), при которых оно обращается в верное равенство или установить, что таких значений нет”. Там же дано определение уравнения как “аналитической записи задачи о разыскивании значений аргументов, при которых значения двух функций равны”.
Понятно, что под аналитической записью и понимается запись равенства, левая или правая части которого содержат неизвестную (неизвестные) букву (или число). Именно буквенное выражение определяет функцию от входящих в него букв, заданную на допустимых числовых значениях.
Введение записи задачи (о нахождении неизвестной величины) с помощью уравнения начинается с конкретной задачи. Способы составления и решения уравнений опираются на отношение целого и его частей, а не на 6 правил нахождения неизвестных при сложении, вычитании, умножении, делении.
Для того, чтобы найти способ решения уравнения, достаточно определить сначала по схеме, а позже и сразу по формуле, чем является неизвестная величина: частью или целым. Если известная величина является целым, то для ее нахождения нужно сложить, а если она часть, то из целого нужно вычесть известные части. Таким образом, ребенку не нужно запоминать правила нахождения неизвестного слагаемого, уменьшаемого и вычитаемого.
Успешность ребенка, его навык при решении уравнений будут зависеть от того, может ли ребенок переходить от описания отношения между величинами с помощью схемы к описанию с помощью формулы и наоборот. Именно этот переход от уравнения как одного из вида формул к схеме и определения с помощью схемы характера (часть или целое) неизвестной величины являются теми основными умениями, которые дают возможность решать любые уравнения, содержащие действия сложения и вычитания. Другими словами, дети должны понять, что для правильного выбора способа решения уравнения, а значит, и задачи нужно уметь видеть отношение целого и частей в чем и поможет схема. Схема здесь выступает в качестве средства решения уравнения, а уравнение, в свою очередь, как средство решения задачи. Поэтому большинство заданий ориентировано на составление уравнений по заданной схеме и на решение текстовых задач путем составления схемы и с ее помощью составления уравнения, позволяющего найти решение задачи.
Традиционная школа.
Изучение уравнений в начальных классах традиционной школы происходит в несколько этапов. Программой традиционной школы предусмотрено знакомство детей с уравнениями первой степени с одной неизвестной. Большое значение в плане подготовки к введению уравнений имеют упражнения на подбор пропущенного числа в равенствах, деформированных примерах, вида 4+€=5, 4–€=2, €–7=3, и т.п. в процессе выполнения таких упражнений дети привыкают к мысли, что неизвестным может быть не только сумма или разность, но и одно из слагаемых (уменьшаемое или вычитаемое). До 2 класса неизвестное число обозначается, как правило, так: €, ?, *. Теперь же для обозначения неизвестного числа используют буквы латинского алфавита. Равенство вида 4 + х = 5 называют уравнением. Равенство, где есть буква, называют уравнением.
На первом этапе уравнения решают на основе состава числа. Учитель знакомит с понятием неизвестного, понятием уравнение, показывает разные формы чтения, учит записывать уравнения по диктовку, разбирает понятия “решить уравнение”, “что называется корнем”, “что есть решение уравнения”, учит проверять решенные уравнения.
На втором этапе решение уравнений происходит с использованием зависимости между компонентами. В этом случае при нахождении неизвестного числа можно пользоваться приемом замены данного уравнения равнозначным ему уравнением. Опорой перехода может быть граф. Приведу примеры уравнений и замены их равнозначными уравнениями с опорой на графы.
х × 4 = 16
х = 16 : 4
х = 4
4 × 4 = 16
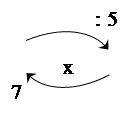 х : 5 = 7 х : 5 = 7
х = 7 × 5
х = 35
35 : 5 = 7
После того как учащиеся научатся решать простейшие уравнения, включаются более сложные уравнения видов: 48 – х = 16 + 9, а – (60 – 14) = 27, 51 – (х + 15) = 20, решение которых выполняется также на основе взаимосвязи между результатами и компонентами арифметических действий, ведется подготовка к решению задач способом составления уравнений. Для решения таких уравнений необходимы знания порядка действий в выражении, а также умения выполнять простейшие преобразования выражений. Уравнения указанных видов вводятся постепенно. Сначала простейшие уравнения усложняются тем, что их правая часть задается не числом, а выражением. Далее включаются уравнения, в которых известный компонент задан выражением. Полезно учить читать эти уравнения с названием компонентов. Наконец, приступают к решению таких уравнений, где один из компонентов является выражением, включающим неизвестное число, например: 60 – (х + 7) = 25, (12 – х) + 10 = 18.
При решении уравнений такого вида приходится использовать дважды правила нахождения неизвестных компонентов. Рассмотрим.
Обучение решению таких уравнений требует длительных упражнений в анализе выражений и хорошего знания правил нахождения неизвестных компонентов. На первых порах полезны упражнения в пояснении решенных уравнений. Кроме того, следует чаще решать такие уравнения с предварительным выяснением, что неизвестно и какие правила надо вспомнить, чтобы решить данное уравнение. Такая работа предупреждает ошибки и способствует овладению умением решать уравнения.
Особое внимание следует уделять проверке решения уравнения. Учащиеся должны четко знать, усвоить последовательность и смысл действий, выполняемых при проверке: найденное число подставляют вместо буквы в выражение, затем вычисляют значение этого выражения и, наконец, сравнивают его с заданным значением или с вычисленным значением выражения, стоящего в другой части уравнения. Если получаются равные числа, значит, уравнение решено верно.
Дети могут выполнять проверку устно или письменно, но при этом всегда должны быть четко выделены основные ее звенья: подставляем…, вычисляем…, сравниваем…
2.7. Методика обучения решению текстовых
задач
Традиционная школа.
Уравнения используются для решения задач. Существует правило составления уравнения:
Выясняется, что известно, что неизвестно.
Обозначение неизвестного за х.
Составление уравнения.
Решение уравнения.
Полученное число истолковывается в соответствии с требованием задачи.
Необходимым требованием для формирования умения решать задачи с помощью уравнений является умение составлять выражения по их условиям. Поэтому вводится запись решения задач в виде выражения. Учащиеся упражняются в объяснении смысла выражений, составленных по условию задачи; сами составляют выражения по заданному условию задачи, а также составляют задачи по их решению, записанному в виде выражений.
Одним из самых трудных моментов является запись задачи в виде уравнения, поэтому вначале при составлении уравнения широко используются средства наглядности: рисунки, схемы, чертежи.
Для формирования у учащихся умения решать задачи алгебраическим способом необходимо, чтобы они могли решать уравнения, составлять выражения по задаче и осознавать сущность процесса “уравнивания неравенств”, т.е. преобразования неравенства в уравнение. Уже на первых уроках дети, сравнивая два множества, устанавливают, в каком из них содержится больше элементов и что нужно сделать, чтобы в обоих множествах было одинаковое их количество.
Вместе с тем возможности использования алгебраического метода решения текстовых задач в начальных классах традиционной школы ограничены, поэтому арифметический способ остается в традиционной школе основным.
Система РО.
Сначала учитель читает задачу для общего ознакомления, а затем вновь переходит к чтению, но “по частям”. Учитель (и только учитель!) читает такую часть текста, которая позволяет ребенку нарисовать элемент будущей схемы, затем следующие часть – и опять дети изображают часть схемы, и т.д. Начертив схему, дети должны заменить буквой (х, y, z) неизвестную величину, после чего приступать к анализу отношений между известными и неизвестными величинами.
Схема, которую дети составят к данной задаче, фактически является моделью (обратите внимание на то, что на схеме всегда отсутствует наименование), т.к. с ее помощью может быть решена не только данная задача, а целый класс частных задач. Моделирование (с помощью сначала схем, а затем буквенных формул) как учебное действие служит средством выделения отношений при анализе условий конкретных задач, а сама графическая или (и) беквенно-знаковая модель является средством фиксации выделенных отношений (см. приложении ).
Итак, процесс решения текстовой задачи с буквенными данными в течение первых трех лет мы будем осуществлять в семь этапов.
I этап – это перевод условия задачи в графическую модель, т.е. в схему. Кстати, схема, в отличие от чертежа, не требует, во-первых, специальных чертежных инструментов, и, во-вторых, точного соблюдения заданных отношений. Схема может выполняться от руки, указывать и отображать заданные отношения;
II этап – это преобразование одной графической модели в другую. Этот этап может быть пропущен, если необходимости в преобразовании нет изначально, либо она отпала в связи со свернутостью действия;
III этап – составление буквенно-знаковой модели (формулы), т.е. составление уравнения.
Когда ребенок переходит от схемы к составлению уравнения, то бывают, при правильно построенной схеме, ошибки в описании отношений (заданных через схему) в знаковой форме, т.е. с помощью уравнения. Чтобы предупредить эти ошибки, нужно использовать те значки, которые мы использовали, когда работали над переходом от текста к схеме, от схемы к преобразованной схеме и от нее к знаковой форме. Это были вспомогательные значки – “дорожки”.
Например:
“В три магазина привезли а кг. печенья, во второй – на в кг больше, чем в первый, а в третий – на с кг меньше, чем во второй. Сколько кг печенья привезли в каждый магазин?”
Строим ступенчатую схему, затем обозначаем первую величину буквой х (так удобнее)
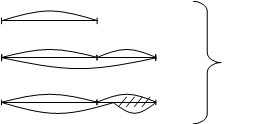 х х
х в
х в
? с
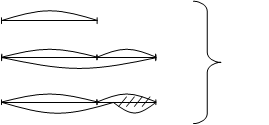 Если мы сразу переходим от ступенчатой схемы к описанию в виде формулы, то дети часто теряют элементы схемы, компоненты действий. Это самая распространенная ошибка. Чтобы устранить ошибки такого характера. Чтобы научить ребенка видеть каждую часть входящую в это целое, мы вводим этап преобразования схемы (II этап). Мы преобразовываем ступенчатую схему в схему линейную. Чтобы ничего не потерять, введем “дорожку” от элемента схемы к развертке. Если мы сразу переходим от ступенчатой схемы к описанию в виде формулы, то дети часто теряют элементы схемы, компоненты действий. Это самая распространенная ошибка. Чтобы устранить ошибки такого характера. Чтобы научить ребенка видеть каждую часть входящую в это целое, мы вводим этап преобразования схемы (II этап). Мы преобразовываем ступенчатую схему в схему линейную. Чтобы ничего не потерять, введем “дорожку” от элемента схемы к развертке.

х  х в х в
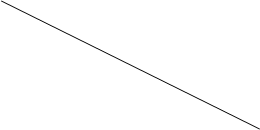 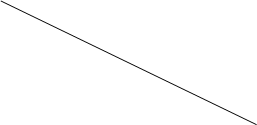 х в х в
 ? с ? с
  а а
с
х х в х в
С помощью “дорожек” ребенок следит, чтобы каждый элемент ступенчатой схемы входил в общую линейную схему, в общую величину. Постепенно эти “дорожки” уходят, становятся не нужны, т.к. ребенок видит все части составляющие целую величину. При переходе от линейной системы к составлению уравнения опять могла произойти потеря. Чтобы проверять самих себя, мы “дорожками” показываем каждый элемент равенства:
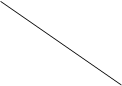 а а
 с с
 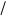  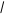  х х в х в х х в х в
3х + 2в – с = а
Если дети научились видеть, из чего состоит линейная схема, то преобразовывать ступенчатую схему в линейную не нужно. Если ребенок научился действовать, то никакие дорожки ему не нужны. Но если вы возвращаетесь к анализу того, какие ошибки могут быть и как их обнаружить, то тогда те значки, которые были на этапе обучения ребенка, ребенок использует вновь для самоконтроля и для самопроверки.
Задача состоит в том, чтобы сформировать у ребенка действие самоконтроля.
Как будет выглядеть наша картинка
если не сформировано: если сформировано
выполняю проверяю выполняю проверяю
 IV этап – решение составленного уравнения. Этап может совпасть с предыдущим, если ребенок записывает уравнение сразу в форме решения: х = выражение ; IV этап – решение составленного уравнения. Этап может совпасть с предыдущим, если ребенок записывает уравнение сразу в форме решения: х = выражение ;
V этап – это подбор вместо букв подходящих чисел. Подходящих с трех точек зрения:
сюжет задачи;
выполнимости арифметического действия;
умения успешно оперировать с подобранными числами.
Другими словами, речь идет об области допустимых значений по отношению к сюжету и т.д.
VI этап – выполнение необходимых вычислений, требующих последовательного выполнения арифметических действий с числами.
VII этап – возвращение к условию задачи для получения ответа на вопрос ее, т.к. не всегда величина, которую обозначили буквой х и относительно которой составляется и решается уравнение, может совпадать с величиной, которую нужно найти для ответа на вопрос задачи. Решив уравнение, необходимо его проверить, получен ли ответ на вопрос задачи.
Итак, выделено семь этапов, хотя основными являются четыре: построение схемы, составление и решение уравнения и вычисление числового значения.
2.8. Диагностика и контроль в системе РО
Нами были проведены экспериментальные исследования, которые проводились во 2-ом классе РО и 2-ом классе традиционного обучения.
Основная задача состояла в том, чтобы проанализировать качество усвоения математических знаний.
Детям были даны три задания по теме “Решение уравнений” (см. приложение 4), а также три текстовые задачи (см. приложение5).
Анализ результатов свидетельствуют о том, что учебная деятельность в системе РО способствует интенсивному развитию теоретического мышления. У детей экспериментальных классов повысился уровень общего развития, а также в значительной мере увеличилось качество обученности. В результате учебной деятельности школьники получают новые знания, двигаются вперед в своем развитии.
Про методику проведения уроков, приемы с способы РО можно говорить много, но вот несколько высказываний родителей:
“Нас впечатляет способность Ирины решать сложные проблемы простым способом, пусть и по-своему, но всегда правильно”.
“У славы обо всем есть свое мнение, которое он всегда отстаивает”.
“Мне нравится, что сын при решении любой проблемной ситуации анализирует возможные варианты” и т.д.
Становление человека осуществляется в начальной школе.
Главная цель учителя – научить детей учиться – в классах РО достигается на выходе в среднее звено. Поэтому школьники могут учиться в любой школе и в любом классе. Рядом с ними меняется сам учитель. А это хорошо, если учитель наконец задумается над тем, с каким запасом знаний он придет к детям, будет ли он интересен им как человек.
Хочется дать советы учителям и родителям:
Умей мечтать, не став рабом мечтаний,
И мыслить, мысли не обожествив,
Равно встречай успех и поруганье,
Не забывая, что их голос лжив.
Имей принудить сердце, нервы, тело
Тебе служить, когда в твоей груди
Все пусто, все у же сгорело,
И только говорит – иди.
Р. Киплинг
Старайтесь найти в ребенке то, за что его можно похвалить, а не то, за что поругать.
Знайте, что ребенку тогда интересно с вами, когда вам интересно с ним.
Давайте возможность каждому ребенку сделать свое маленькое открытие.
Если ребенку тяжело, то найдите для него такое задание, которое ему по силам.
Не навязывайте ребенку своих форм работы, он должен выбрать их сам.
Чем выше уровень эмоционального комфорта, тем больше шансов на успех в учебе.
Вместо отметок – главной причины школьных бед (они акцентируют в большей степени провалы в учебе, чем успех) - пользуйтесь рекомендуемой системой оценок в РО.
Помните, что ошибка одного может породить мысль другого. Не пугайтесь детских ошибок.
Не бойтесь сделать вид, что вы что-то не понимаете, этому всегда можно и нужно найти разумное обоснование.
Не бойтесь признаться в том, чего сами не знаете.
Не пытайтесь объяснить ребенку то, до чего он может додуматься сам.
Вступайте в диалог с детьми только в том случае, если у вас есть разумные аргументы “за” или “против” высказываний детей.
Не требуйте от ребенка словесных формулировок и обобщений до того, как он выполнит предметное действие или какое-либо задание.
Знайте, что учебники носят рефлексивный характер: дети вместе со взрослыми конструируют их содержание. Ребенок работает не с картинками из учебников, а с реальными предметами (фигурами), изображенными в нем.
Помните, что неудачи в жизни имеют две причины – недостаток любви и заниженная самооценка, а значит, ребенок особенно нуждается в чувстве собственного достоинства. Просто любите детей и не бойтесь им показать это.
Владей собой среди толпы смятенной,
Верь сам в себя наперекор вселенной
И маловерным отпусти им грех.
Пусть час не пробил, жди не уставая,
Пусть лгут жрецы, не снисходи до них,
Умей прощать и не кажись, прощая,
Великодушней и мудрей других. (Р. Киплинг)
1. Выготский Л.С. Педагогическая психология / Под ред. В.В. Давыдова. М.: Педагогика, 1991
2. Воронцов А.Б. Практика развивающего обучения по системе Д.Б. Эльконина – В.В. Давыдова. М: ЦПФО “Развитие личности”,1998
3. Давыдов В.В. Виды обучения. М.: Интор, 1996
4. Давыдов В.В. Проблемы развивающего обучения. М.: Педагогика, 1997
5. Давыдов В.В. Теория развивающего обучения. М.: Интор, 1999
6. Давыдов В.В. Учебная деятельность и развивающее обучение //Давыдов В.В. Последние выступления. ПЦ “Эксперимент”,1998
7. Основы общей психологии. М., 1991
8. Дусавицкий А.К. Развитие личности в учебной деятельности. М.: Дом педагогики, 1996
9. Российская педагогическая энциклопедия: в 2-х т. /Гл. ред. В.В. Давыдов. М.: Большая Российская энциклопедия, 1993, 1998
10. Цукерман Г.А. Виды общения в обучении. Томск: Пеленг, 1993
11. Чуприкова Н.А. Умственное развитие и обучение: психологические основы развивающего обучения. М.: АО “Столетие”, 1995
12. Информационно-методический журнал “Феникс”. – 1997 - №6, - 1995 - №3 – (межрегиональный вестник развития личности)
13. Эрдниев П.М. Обучение математике в начальных классах.
14. А.А. Столяр. Методика начального обучения математике.
15. Давывыдов В.В., Горбов С.Ф., Микулина Г.Г. “Обучение математике”. М.: Мирос, 1999
16. Александрова Э.И. “Методика обучения математике в начальной школе”. М.: Вита-Пресс, 1999
17. Александрова Э.И. Математика. М.: “Дом педагогики”, 2000
18. Александрова Э.И. Учебные тетради по математике. М.: “Дом педагогики”, 2000
19. Александрова Э.И. Развивающие прописи. М.: “Дом педагогики”, 2000
20. Давывыдов В.В., Горбов С.Ф., Микулина Г.Г. Математика. М.: “Дом педагогики”, 2000
21. Микулина Г.Г. Учимся понимать математику. М.: “Дом педагогики” 2000
22. Захаров А. М., Фещенко Т.И. Математика. М.: “Дом педагогики” 2000
23. Пачатковая школа 2001 - № 6, 11
|