Оглавление
Введение..............................................................................................................3
Глава 1. Теоретико-методологические основы систематизации и обобщений знаний учащихся..................................................................................................5
1.1. Цели и функции систематизации в процессе обучения.............................5
1.2. Принципы и типы систематизации и обобщения......................................8
1.3. Средства и методы осуществления систематизации и обобщения на уроках математики.............................................................................................17
Глава 2. Экспериментальное исследование методов и приемов систематизации и обобщения знаний учащихся при изучении темы «Алгебраические уравнения» в 9 классе...........................................................26
2.1. Тематическое планирование........................................................................26
2.2. Планы-конспекты уроков.............................................................................32
2.3. Результаты эксперимента.............................................................................41
Заключение...........................................................................................................47
Список литературы...............................................................................................48
Введение
Систематизация знаний учащихся является составной частью процесса обучения. По определению систематизация - это соотношение достигнутых результатов с запланированными целями обучения. Некоторые учителя традиционно подходят к организации систематизации и обобщения знаний учащихся, используют его в основном ради показателей достигнутого. Форма знаний учащихся должна давать сведения не только о правильности или неправильности конечного результата выполненной деятельности, но и о ней самой: соответствует ли форма действий данному этапу усвоения. Правильно поставленная систематизация учебной деятельности учащихся позволяет учителю оценивать получаемые ими знания, умения, навыки, вовремя оказать необходимую помощь и добиваться поставленных целей обучения. Все это в совокупности создает благоприятные условия для развития познавательных способностей учащихся и активизации их самостоятельной работы на уроках математики.
Реклама

Хорошо поставленная систематизация знаний учащихся позволяет учителю не только правильно оценить уровень усвоения учащимися изучаемого материала, но и увидеть свои собственные удачи и промахи.
Наша задача проверить не только знания, но и элементы практического усвоения, ощущения учащимися нового материала.
Поэтому нами введены новые элементы систематизации знаний:
1. Типы систематизации (знания и умения)
2. Виды систематизации (предварительная, текущая, итоговая)
3. Зачетная система (работа с экспертами)
4. Новое планирование темы
Проблема систематизации знаний учащихся не нова, и педагогический опыт, накопленный в этой области богат и разносторонен. В этой работе систематизированы накопленные сведения по проблеме систематизации и обобщения знаний учащихся. Эта система сведений применена при изучении темы «Алгебраические уравнения» в 9 классе.
Цель исследования:
разработать и экспериментально проверить систему систематизации и обобщения знаний учащихся.
Объект исследования:
процесс обучения в общеобразовательной школе.
Предмет исследования:
Различные формы систематизации знаний учащихся по математике.
Без хорошо налаженной формы и своевременной оценки результатов нельзя говорить об эффективности обучения математике.
В ходе исследования выдвинута гипотеза:
«Если учитель будет систематически, всесторонне использовать различные формы систематизации и обобщения знаний и умений, то будет повышаться заинтересованность учащихся в изучении предмета, а, следовательно, будет повышаться и качество обучения».
Задачами
данной работы являются:
1) Изучение литературы по проблеме систематизации знаний учащихся.
2) Систематизирование накопленных сведений по проблеме систематизации знаний учащихся.
3) Разработка методики применения различных форм систематизации и обобщения знаний учащихся по теме «Алгебраические уравнения».
Глава 1. Теоретико-методологические основы систематизации и обобщений знаний учащихся
1.1. Цели и функции систематизации в процессе обучения
Основная цель систематизации знаний и умений состоит в обнаружении достижений, успехов учащихся; в указании путей совершенствования, углубления знаний, умений, с тем, чтобы создавались условия для последующего включения школьников в активную творческую деятельность[5, с. 62].
Реклама

Эта цель в первую очередь связана с определением качества усвоения учащимися учебного материала – уровня овладения знаниями, умениями и навыками предусмотренных программой по математике. Во – вторых, конкретизация основной цели систематизации связана с обучением школьников приемам взаимосистематизации и самосистематизации, формированием потребности в самоконтроле и взаимоконтроле.
В - третьих эта цель предполагает воспитание у учащихся таких качеств личности, как ответственность за выполненную работу, проявление инициативы.
Если перечисленные цели систематизации знаний и умений учащихся реализовать, то можно говорить о том, что систематизация выполняет следующие функции[13, с. 27]:
1. Контролирующую.
2. Обучающую (образовательную).
3. Диагностическую.
4. Прогностическую.
5. Развивающую.
6. Ориентирующую.
7. Воспитывающую.
Контролирующая функция
Контролирующая функция состоит в выявлении состояния знаний и умений учащихся, уровня их умственного развития, в изучении степени усвоения приемов познавательной деятельности, навыков рационального учебного труда.
При помощи систематизации определяется исходный уровень для дальнейшего овладения знаниями, умениями и навыками, изучается глубина и объем их усвоения. Сравнивается планируемое с действительными результатами, устанавливается эффективность используемых учителем методов, форм и средств обучения[11, с. 13].
Обучающая функция
Обучающая функция систематизации заключается в совершенствовании знаний и умений, их систематизации. В процессе формы учащиеся повторяют и закрепляют изученный материал. Они не только воспроизводят ранее изученное, но и применяют знания и умения в новой ситуации.
Форма помогает школьникам выделить главное, основное в изучаемом материале, сделать проверяемые знания и умения более ясными и точными. Систематизация способствует также обобщению и систематизации знаний.
Диагностическая функция
Сущность диагностической функции систематизации – в получении информации об ошибках, недочетах и пробелах в знаниях и умениях учащихся и порождающих их причинах затруднений учащихся в овладении учебным материалом, о числе, характере ошибок. Результаты диагностических проверок помогают выбрать наиболее интенсивную методику обучения, а также уточнить направление дальнейшего совершенствования содержания методов и средств обучения[21, с. 17].
Прогностическая функция
Прогностическая функция формы служит получению опережающей информации об учебно-воспитательном процессе. В результате формы получают основания для прогноза о ходе определенного отрезка учебного процесса: достаточно ли сформированы конкретные знания, умения и навыки для усвоения последующей порции учебного материала (раздела, темы).
Результаты прогноза используют для создания модели дальнейшего поведения учащегося, допускающего сегодня ошибки данного типа или имеющего определенные пробелы в системе приемов познавательной деятельности.
Прогноз помогает получить верные выводы для дальнейшего планирования и осуществления учебного процесса.
Развивающая функция
Развивающая функция систематизации состоит в стимулировании познавательной активности учащихся, в развитии их творческих способностей. Систематизация обладает исключительными возможностями в развитии учащихся. В процессе систематизации развиваются речь, память, внимание, воображение, воля и мышление школьников. Систематизация оказывает большое влияние на развитие и проявление таких качеств личности, как способности, склонности, интересы, потребности.
Ориентирующая функция
Сущность ориентирующей функции систематизации - в получении информации о степени достижения цели обучения отдельным учеником и классом в целом – насколько усвоен и как глубоко изучен учебный материал. Систематизация ориентирует учащихся в их затруднениях и достижениях.
Вскрывая пробелы, ошибки и недочеты учащихся, он указывает им направления приложения сил по совершенствованию знаний и умений. Систематизация помогает учащемуся лучше узнать самого себя, оценить свои знания и возможности[11, с. 28].
Воспитывающая функция
Воспитывающая функция систематизации состоит в воспитании у учащихся ответственного отношения к учению, дисциплины, аккуратности, честности.
Форма побуждает школьников более серьезно и регулярно контролировать себя при выполнении заданий. Она является условием воспитания твердой воли, настойчивости, привычки к регулярному труду.
Выделение функции систематизации подчеркивает его роль и значение в процессе обучения. В учебном процессе сами функции проявляются в разной степени и различных сочетаниях. Реализация выделенных функций на практике делает систематизация более эффективным, а также эффективней становится и сам учебный процесс.
1.2. Принципы и типы систематизации и обобщения
Систематизация должна быть целенаправленной, объективной, всесторонней, регулярной и индивидуальной. Раскроем эти принципы систематизации подробнее[14, с. 18].
а) Целенаправленность предполагает четкое определение цели каждой формы. Постановка цели определяет всю дальнейшую работу по обоснованию используемых форм, методов и средств систематизации. Цели систематизации предполагают ответы на следующие вопросы: что должно проверяться, кто должен опрашиваться, какие выводы можно будет сделать на основе результатов формы, какой ожидается эффект от проведения формы. При конкретизации целей систематизации исходят из целей воспитания, развития и обучения учащихся, которые реализуются на данном этапе обучения.
б) Объективность систематизации предупреждает случаи субъективных и ошибочных суждений, которые искажают действительную успеваемость учащихся и снижают воспитательное значение систематизации. Объективность систематизации зависит от многих факторов. Среди них выделяют следующие: четкое выделение общих и конкретных целей обучения, обоснованность выделения и отбора объектов и содержания систематизации, обеспеченность методами обработки, анализа и оценивания результатов систематизации, организованность проведения систематизации. От решения этих вопросов во многом зависит объективность и качество систематизации.
в) Под всесторонностью систематизации понимается охват большого по содержанию проверяемого материала. Этот принцип включает в себя усвоение основных идей данного курса, и усвоение учебного материала по определенным содержательным, стержневым линиям курса, и знание учащимися отдельных и существенных фактов, понятий, закономерностей, теорем, способов действий и способов деятельности. При таком обилии проверяемого материала усложняется методика составления заданий, т.е. предъявляются повышенные требования к методике выделения и сбора объектов формы.
г) Под регулярностью подразумевается постепенная систематизация, которая сочетается с самим учебным процессом.
Индивидуальность систематизации требует оценки знаний, умений, навыков каждого ученика.
Типы систематизации
В зависимости от того, кто осуществляет систематизацию за результатами деятельности учащихся, выделяют следующие три типа систематизации[22, с. 27]:
Внешний
(осуществляется учителем над деятельностью ученика)
Взаимный
(осуществляется учеником над деятельностью товарища)
Самосистематизация
(осуществляется учеником над собственной деятельностью)
Внешняя систематизация
В процессе систематизации учителем знаний и умений учащихся выделяют следующие компоненты:
1. Уточнение целей изучения данного отрезка учебного материала и
установление конкретного содержания систематизации.
2. Различные способы выражения результатов систематизации: оценка и
отметка.
3. Выбор видов, форм, способов и средств систематизации,
соответствующих поставленным целям.
Содержание систематизации
Установление содержания систематизации зависит от целей изучения данного отрезка учебного материала. Существуют различные подходы к описанию целей и содержанию, чтобы они служили основой для разработки средств для систематизации знаний и умений учащихся[16, с. 33].
Рассмотрим 2 из них:
Первый подход связан с указанием тех качеств, которые должны быть присущи сформированным в результате обучения знаниям и умениям учащихся: полноте, глубине, обобщенности, осознанности.
Второй подход связан с указанием уровней усвоения знаний и соответствующим им видам деятельности. Выделяют следующие уровни усвоения материала: узнавание, запоминание, воспроизведение.
Оценка и отметка
Процесс систематизации знаний и умений учащихся связан с оценкой и отметкой. Следует различать эти понятия.[1, с. 56]]
Оценка
– это процесс, действие (деятельность) оценивания, которое осуществляется человеком.
Отметка
выступает как результат этого процесса (результат действия), как его условно формальное выражение.
Существуют различные способы оценивания в зависимости от того, с чем производится сравнение действий ученика при оценке. Если сравниваются действия, производимые учеником в настоящем, с аналогичными действиями, произведенными этим же учеником в прошлом, то мы имеем личностный способ оценивания. Если сравнение происходит с установленной нормой (образцом) выполнения действий, то обращаемся к нормативному способу. В случае сопоставительного способа оценивания происходит сравнение действий ученика с аналогичными действиями других учеников.
В текущей учебной работе учитель, как правило, использует личностный способ оценивания; при подведении итогов изучения темы, итогов четверти и т.д. – нормативный.
Оценка и отметка определяются знаниями и умениями ученика, которые он показал в процессе систематизации. Одним из показателей, по которому учитель имеет возможность судить об этих знаниях, умениях, служат погрешности, допущенные учащимися при работе со средствами систематизации, предложенными учителем.
Погрешности делят на ошибки и недочеты.
Ошибка
– это погрешность, свидетельствующая о том, что ученик не овладел теми знаниями и умениями (связанными с контролируемым разделом, темой), которые определены программой по математике для средней школы.
Недочетом
считают погрешность, указывающую либо на недостаточно полное, прочное усвоение основных знаний и умений, либо на отсутствие знаний, которые программой не относятся к основным. К недочетам относят также неаккуратность при записи решения, небрежное выполнение чертежа при решении задачи и т.д.
Приведенное деление погрешностей на ошибки и недочеты является условным. Размытость границы между ошибкой и недочетом может быть одной из причин необъективной оценки знаний и умений ученика.[11, c.42-56]
Формы систематизации
В соответствии с формами обучения на практике выделяют 3 формы систематизации: индивидуальная, групповая и фронтальная.[4, с. 44]]
1. Индивидуальная систематизация.
При индивидуальном контроле каждый ученик получает свое задание, которое он должен выполнить без посторонней помощи. Такая форма систематизации целесообразна в случае, если требуется выяснить индивидуальные знания, способности и возможности отдельных учащихся.
Такая форма систематизации всегда планируется: учитель намечает, когда, кого, с какой целью спросить и какие для этого использовать средства.
2. Групповая систематизация.
При проведении такой систематизации знаний класс временно делится на несколько групп (от 2 до 10 учащихся) и каждой группе дается проверочное задание. В зависимости от цели систематизации группам предлагают одинаковые или разные задания.[23, с. 13]]
Групповую форму систематизации применяют:
а) При повторении с целью обобщения и систематизации учебного материала.
б) При выделении приемов и методов решения задач
в) При выявлении наиболее рационального решения задач или доказательства теорем.
Иногда групповую систематизацию проводят в виде уплотненного опроса.
3. Фронтальная систематизация.
При фронтальном контроле задания предлагаются всему классу. В процессе этого систематизации изучается правильность восприятия и понимания учебного материала, вскрываются слабые стороны в знаниях учащихся, обнаруживаются недочеты, пробелы, ошибки в работах и ответах учащихся. Это позволяет учителю вовремя наметить меры по их преодолению и устранению.
Взаимная систематизация
Роль взаимного систематизации качества и эффективности учебной деятельности школьников трудно переоценить.
Он содействует выработке таких качеств личности, как честность и справедливость, коллективизм. Взаимная систематизация помогает также учителю осуществлять форму знаний учащихся. В массовой школе сравнительно часто используется взаимная форма организационной готовности к уроку (констатирующая взаимосистематизация выполнения домашнего задания) и частичная, эпизодическая взаимоформа знаний учащихся (рецензирование ответов на уроке, рецензирование письменных работ). Систематическая же взаимная форма знаний, умений, навыков применяется весьма редко. Остановимся на методике проведения этой формы.[5, с. 26]]
Каждый ученик получает карточку с вопросом, ответ на который он должен знать хорошо; на обороте карточки записаны фамилии нескольких учащихся и даты, когда они будут опрошены по этому вопросу. В каждый из указанных дней владелец карточки задает свой вопрос одному из учеников, в то же время он и сам должен ответить на вопрос, помещенный в карточке этого ученика. За день до формы учащиеся предупреждают друг друга, на какие вопросы им придется отвечать. Взаимоформа проводится обычно в последние три минуты каждого урока. За правильный ответ против фамилии (на обороте карточки) ученик ставит знак плюс, за неверный ответ или отказ отвечать – минус. Учитель периодически просматривает карточки взаимоформы. В тех случаях, когда оказывалось много минусов, проводилась дополнительная взаимоформа этих учеников во внеурочное время. В конце четверти проводится систематизационый опрос всех учащихся, который позволяет выяснить не только общий уровень их знаний, но и насколько справедливо и строго каждый из них спрашивал своих одноклассников.
Взаимоформа знаний значительно активизирует деятельность учащихся, повышает интерес к знаниям и даже нравится им. В ходе взаимного систематизации раскрываются индивидуальные особенности детей, их взаимоотношения с товарищами.
Самосистематизация
На хорошем уроке всегда есть своя сверхзадача, которая сводится к формированию этих навыков и меняется в зависимости от темы урока. В одном случае она состоит в обучении приемам анализа, умению видеть закономерности, ставить вопросы, делать выводы.
В другом - в формировании критического отношения учащихся к результатам своей работы, требовательности к себе. Постоянного внимания учителя требует и проблема воспитания у учащихся веры в свои способности. Известно, что многие ученики боятся приступать к решению задач, алгоритм решения которых им неизвестен. Иногда проявляется страх перед трудностями, неумение преодолевать их самостоятельно. Выход здесь только один – прививать учащимся умения и навыки самосистематизации. Это важно с воспитательной, психолого-педагогической точки зрения. Ведь при этом ученики фактически участвуют в управлении своей собственной учебной деятельностью. Это порождает у них удовлетворенность своими занятиями, своей работой, позволяет им поверить в себя, в свои познавательные способности, открывает простор для творческой инициативы и самостоятельности. Укажем приемы формирования критического отношения учеников к результатам своей работы. Учащимся предлагается рассмотреть решения ряда примеров и оценить их. Обычно эти решения содержат типичные ошибки, которые надо обнаружить. Иногда требуется выяснить, верен ли ответ к заданию. Навыки самосистематизации можно развивать и на занимательных задачах, основанных на обычной житейской смекалке. Их полезно рассматривать как в младших, так и в старших классах. Эти задачи привлекают внимание всех учащихся, даже тех, которые не имеют особых успехов в математике[23, с. 56].
Трудно удержать интерес учащихся к предмету, если преследуется единственная цель: научить школьников выполнять действия по данному образцу. Поэтому наряду с изучением алгоритмов возникает необходимость учить осознанному, творческому их применению. Приведем один распространенный прием такого обучения. Сразу после того, как учащиеся освоили все этапы алгоритма, им предлагается задача, которая решается по изученному алгоритму, но не самым рациональным способом. Более красивое решение получается, если не следовать алгоритму, а просто проанализировать условие задачи и сделать верные выводы.
На уроках геометрии иногда полезно “досочинить” задачу. Обычно для этого выбирают задачу из учебника на доказательство. Выписывают ее условие, а то, что надо доказать, придумывают сами.
Отметим еще несколько приемов работы учителя в формировании потребности в самоконтроле при обучении математике[11, с. 43].
1. Давать определение иногда имеет смысл не в окончательном виде. Более
содержательные беседы с классом получаются тогда, когда ученики предлагают свой вариант определения, который затем уточняется.
2. Почти все упражнения, которые предлагаются ученикам, сформулированы
позитивно (доказать, найти). Появились также упражнения и другого типа (верно ли, проверить), но их очень мало. И совсем нет упражнений на опровержение утверждений, в то время как они чрезвычайно полезны.
Упражнения такого типа легко получить из задач позитивных, особенно на доказательство.
3. Если ученик дал письменное решение задачи (на доске или в тетради) с
ошибкой, то в иных случаях не надо торопиться с выставлением оценки. Если есть возможность дать ему время на нахождение собственной ошибки, то ее нужно использовать. Если ошибка будет найдена, то оценку снижать не стоит.
4. Класс работает самостоятельно. Выборочно просматривая некоторые
решения, учитель видит разнообразные ошибки, наиболее поучительные из них стоит показать всем учащимся класса.
5. На уроке предложена задача и сразу ответ к ней. У кого-то получился
другой ответ. Не стоит спешить с помощью – окажем ее только тогда, когда самостоятельные попытки найти ошибку ни к чему не привели.
6. Весьма рискованный, но заслуживающий внимания прием.
Учитель берется с ходу решать достаточно сложную задачу, причем на доске. Если ее и удается решить, то вряд ли наилучшим способом. Ученики еще раз убеждаются, что первый вариант решения не всегда является наилучшим.
В результате проведения описанной работы у учащихся начинает формироваться потребность в самоконтроле.
Обычным способом организации самосистематизации в процессе обучения математике является указание ответа (известного заранее или сообщаемого учениками друг другу). Некоторым учащимся в случае трудоемких заданий вполне достаточно свериться с окончательным результатом. Другим требуется дать промежуточные ответы. Это помогает им самостоятельно выполнять учебные задания даже в тот момент, когда у них еще не выработаны прочные навыки.
Среди учебных заданий, стимулирующих самосистематизация в работе учащихся, определенное место занимают задания с программированным систематизацией. Такие задания позволяют увеличить интенсивность самостоятельной учебной работы учащихся, удобны для организации фронтальной работы и коллективного обсуждения полученных индивидуальных результатов.
Последовательно работая над привитием умений, связанных с систематизацией и самосистематизацией в математической деятельности учащихся, можно добиться заметных результатов. При этом растет общая математическая культура школьников, их работы и ответы становятся более грамотными.
1.3. Средства и методы осуществления систематизации и обобщения на уроках математики
Среди методов систематизации выделяют: устную форму, форму письменно-графических работ и форму практических работ[14, с. 41].
Устная форма
Устная форма организуется по-разному, в зависимости от ее цели и от содержания проверяемого материала. Среди целевых установок формы можно выделить следующие: проверить выполнение домашнего задания, выявить подготовленность учащихся к изучению нового материала, проверить степень понимания и усвоения новых знаний. В зависимости от содержания она проводится по материалу предшествующего урока или по отдельным разделам и темам курса.
Методика устной формы включает в себя две основные части:
а) составление проверочных вопросов и их задавание
б) ответ учащихся на поставленные вопросы
Составление проверочных вопросов и заданий - важный элемент устной формы. Качество вопросов определяется их содержанием, характером выполняемых учащимися при ответе на вопросы умственных действий, а также словесной формулировкой.
При составлении вопросов всегда исходят из того, что проверять следует те знания, которые являются основными в данном курсе или относительно трудно усваиваются учащимися или которые необходимы для успешного усвоения дальнейших разделов и тем курса. На подбор вопросов оказывает влияние вид формы: для уточнения содержания вопросов для текущей формы необходим анализ связей изучаемого материала с ранее пройденным, а для тематической и итоговой формы - выделение ведущих знаний и способов оперирования ими. Причем устную форму считают эффективной, если она направлена на выявление осмысленности восприятия знаний и осознанности их использования, если она стимулирует самостоятельность и творческую активность учащихся.
Качество вопросов определяется характером умственных действий, которые выполняют учащиеся при ответе на вопрос. Поэтому среди проверочных заданий выделяют вопросы, активизирующие память (на воспроизведение изученного), мышление (на сравнение, доказательство, обобщение), речь. Большое значение имеют проблемные вопросы, которые заставляют применять полученные знания в практической деятельности.
Качество устной формы зависит от подбора, последовательности и постановки вопросов, которые предлагаются, во-первых, каждый вопрос должен быть целенаправленным и логически завершенным, а во-вторых, должен быть предельно сжатым, лаконичным и точным.
Второй составной частью устной формы является ответ учащегося на вопросы. В дидактической литературе выделяются два условия качественного выявления знаний ученика:
1) Ученику никто не мешает (учитель и класс комментируют ответ потом).
2) Создается обстановка, которая обеспечивает наилучшую работу его интеллектуальных сил.
Прерывать ученика можно только в том случае, если он не отвечает на вопрос, а уклоняется в сторону. При оценке ответа ученика обращают внимание на правильность и полноту ответа, последовательность изложения, качество речи.
Приемы устной формы используются на различных этапах урока. Выбор тех или иных приемов во многом предопределяется целью и логикой урока.
Форма письменно – графических работ
Вторым широко применяемым методом систематизации в обучении математике является форма письменно-графических работ. Этот метод имеет свои качественные особенности: большая объективность по сравнению с устной формой, охват нужного числа проверяемых, экономия времени. Применение письменных работ используется для:
1) Формы знания теоретического материала
2) Умения применять его к решению задач
3) Систематизации сформированных навыков
В методике письменно – графических работ выделяют четыре основных этапа, которым надо уделять внимание, это подготовка, организация, проведение, анализ результатов.
При подготовке нужно: вычленить цель формы, отобрать содержание объектов формы, составить проверочные задания. Большую помощь при этом оказывают учебно – методические пособия “Книга для учителя”, “Дидактические материалы”, образцы проверочных работ в журнале “Математика в школе”.
При организации проверочной работы учащимся сообщается – в каких тетрадях ее выполнять, какие задания им предназначены, как озаглавить работу, как оформить решение, время выполнения работы. При этом следить за самостоятельностью выполнения работы каждым учеником.
Анализирование ответов учащихся эффективно тогда, когда оно проводится по определенным схемам (схемам поэлементного анализа). Тщательно проведенный анализ позволяет глубоко изучить пробелы и достижения отдельных учеников, выделить типичные ошибки и основные затруднения учащихся, изучить причины их появления и наметить пути их устранения.
Форма практических работ
С помощью этого метода получают данные об умении учащихся применять полученные знания при решении практических задач, пользоваться различными таблицами, формулами, чертежными и измерительными инструментами, приборами.
Учитель получает отчет ученика, в котором приводится только результат или схематически описаны план практической работы и ее результаты. Это несколько затрудняет форму и оценку каждого действия ученика. Поэтому на практике в проверочном задании приводиться алгоритм его выполнения, что позволяет осуществить такую форму правильности действий ученика. Все работы проверяются, но оцениваются по-разному, по результатам обзорных работ оценки выставляются в журнал, по результатам тренировочных работ можно выставить лишь положительные оценки.
Средства осуществления систематизации
В настоящее время создаются и распространяются такие средства, которые не требуют больших затрат времени на подготовку, проведение и обработку результатов. Среди них выделяют машинные и безмашинные средства формы[23, с. 74].
Безмашинные средства формы
Среди безмашинных средств формы наиболее распространены в практике работы школы устный опрос учащихся у доски, форма учителем тетрадей с домашним заданием, математический диктант, самостоятельная и систематизационная работы.
Форма домашнего задания
Роль домашних заданий практически обесценивается, если не налажена их форма. Учителя практикуют разные формы учета. Это и устный опрос у доски или с места по домашнему заданию, и короткая письменная работа, но, прежде всего это непосредственная форма задания в тетрадях – фронтальная при обходе класса в начале урока и более основательная, выборочная во внеурочное время.
Форму домашнего задания можно осуществлять в различных формах. Рассмотрим наиболее распространенные приемы формы домашнего задания.
I прием.
У доски готовится один учащийся, класс в это время занят другой работой. Затем ученик отвечает, а остальные слушают и задают вопросы.
II прием.
Отличается от первого тем, что к доске вызывается не один, а все учащиеся. Этот прием позволяет экономить время урока. Этот широко распространенный в школе прием называют уплотненным опросом.
Необходимо отметить недостатки этих приемов:
1) Вызванным учащимся выделяется время на подготовку к ответу.
Остальным не дается время, чтобы продумать ответы на поставленные вопросы.
2) Если вызванные учащиеся отвечают плохо, то уплотненный опрос
затягивается на 15-20 минут, а других учащихся учитель вызвать не может, так как они не готовились к ответу.
Кроме таких форм систематизации выполнения домашнего задания существуют и другие.
Самоформа по образцу применяется на первом уроке после объяснения нового материала. Образец решения домашней работы записан на доске заранее. Учащиеся рассматривают решение образец и устно комментируют его, тетради у всех закрыты. Затем ребята открывают тетради и проверяют свои работы по образцу, подчеркивая ошибки. Этот способ развивает внимание и выявляет ошибки с помощью образца.
Взаимоформа с помощью образца используется на следующем уроке. В этом случае учащиеся проверяют домашнюю работу своего соседа тоже по образцу. Как и в первом случае, окончательно тетради проверяет учитель.
Математический диктант
Математический диктант может заменить опрос по теме, заданной для повторения. Его продолжительность обычно 10-20 минут. Он представляет собой систему вопросов, связанных между собой.
Текст диктанта может быть:
1. Написан на плакате
2. Спроецирован на доску с помощью кадоскопа
3. Зачитан учителем
Существует еще такая разновидность диктанта, как математический диктант с графической записью ответа.
Приведем методику проведения диктанта.
1. Учитель полностью зачитывает текст, а учащиеся слушают, не делая записей.
2. Учитель читает текст по фразам, делая паузы от одной до четырех минут, чтобы дать учащимся возможность выполнить задание.
3. Когда все задания выполнены, учитель снова читает весь текст с небольшими остановками (это дает учащимся возможность что – то исправить и сделать дополнения)
Правильные ответы записываются на доске. Ученики могут проверить диктант самостоятельно у соседа по парте.
В 5-7 классах все работы проверяются учителем. Этот метод формы реже используется в старших классах.
С помощью математического диктанта можно проверить знание учащимися формулировок, определений, свойств, теорем, формул, умения и навыки в их использовании.
Организация самостоятельных работ
При изучении математики важно, чтобы учащиеся не только знали теоретический материал, но и умели применять его к решению задач и упражнений, обладали бы рядом навыков (вычислительными навыками, умениями преобразовывать выражения и т.д.). Эти умения и навыки могут быть по настоящему проверены только в письменной работе. Обычно самостоятельные работы проводятся после коллективного решения задач новой темы и предшествуют систематизационной работе по этой теме.
При проведении самостоятельной работы учитель сталкивается со следующими затруднениями:
1. Дети заканчивают работу не одновременно, поэтому целесообразно включать в работу дополнительные задания для тех, кто работает быстрее.
2. Трудно подобрать задания одинаково посильные всем учащимся.
3. Трудно организовать форму самостоятельных работ.
Организация систематизационных работ
Систематизационная работа может быть кратковременной и долговременной.
1. Перед проведением систематизационной работы необходимо определить объект систематизации, цель предстоящей работы и средства систематизации. Они должны быть сообщены учащимся.
2. В зависимости от вида заданий нужно продумать, каким образом ученик должен их оформить.
3. Учитель должен продумать, что он отнесет к недочетам, а что к ошибкам.
Из этого будет складываться оценка. Критерии оценки хотя бы в общих чертах должны быть известны учащимся.
4. Систематизационная работа должна быть посильной для всех учащихся без исключения. Сильным ученикам нужно дать задания труднее.
5. Каждой систематизационной работе должна предшествовать самостоятельная работа с аналогичными упражнениями.
6. Анализ систематизационной работы необходимо проводить сразу, для этого необходимо завершать работу за несколько минут до звонка. Желательно фрагменты решения разобрать сразу после написания работы, потому что на следующий день или позже учащиеся уже теряют интерес к содержанию работы и многие интересуются только оценкой.
7. Обязательно нужно проводить количественный и качественный анализ систематизационной работы.
Данные количественного анализа удобно представлять в виде таблицы

Но данные количественного анализа не позволяют установить уровень владения материалом конкретного ученика. Такую возможность представляет качественный анализ. Информация, которая подвергается качественному анализу, должна включать данные о выполнении каждого задания предложенной систематизационной работы каждым учеником класса. Такие данные можно фиксировать в таблице.
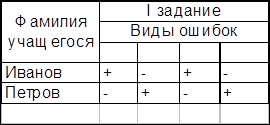
Содержание основной части таблицы свидетельствует об основных ошибках учащихся, допущенных при выполнении отдельных заданий.
Анализ результатов систематизационной работы может способствовать получению выводов об особенностях своей деятельности по организации усвоения школьниками учебного материала.
Машинные средства формы
Для систематизации знаний учащихся используют персональный компьютер. Для систематизации знаний учащихся удобно применять типовые расчеты, которые включают наиболее характерные задания базового курса математики. Перечислим некоторые преимущества использования компьютера для создания типовых расчетов:
1. Однотипные задания печатаются в любом количестве неповторяющихся вариантов;
2. Варианты, созданные с помощью компьютерных программ, проверяются значительно быстрее, так как компьютер может предоставить ответы к каждому заданию;
3. Компьютерные типовые задания удобны для отработки необходимых навыков с отстающими учащимися (учитель не тратит время на подбор однотипных заданий для отработки определенных навыков);
4.Учащиеся с огромным интересом работают с такими заданиями, особенно, если карточка с заданием индивидуальна и ученик может работать в ней.
Глава 2. Экспериментальное исследование методов и приемов систематизации и обобщения знаний учащихся при изучении темы «Алгебраические уравнения» в 9 классе
2.1. Тематическое планирование
Одним из существенных моментов в организации обучения является систематизация за знаниями и умениями учащихся. От того, как она организована, на что нацелена, существенно зависит содержание работы на уроке, как всего класса в целом, так и отдельных учащихся. Вся система систематизации знаний и умений учащихся должна планироваться таким образом, чтобы охватывались все обязательные результаты обучения для каждого ученика. Одновременно в ходе систематизации надо дать учащимся возможность проверить себя на более высоком уровне, проверить глубину усвоения материала. В ходе изучения темы учитель проверяет результаты обучения путем проведения текущих самостоятельных работ, устного опроса, систематизационных работ и других форм систематизации.
История развития математического знания даёт возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры.
Требования к знаниям и умениям учащихся в данном курсе не завышены. Так как чрезмерность требований порождает перегрузку, что ведёт к угасанию интереса к математике. Применение компьютерной технологии (презентации, слайды, поиск информации по имеющимся источникам) заинтересовывает учащихся данным курсом, что, помогая лучше овладеть ЗУН. Курс оснащён информационно-программным средством “Этот удивительный мир чисел, электронная версия”.
Цели курса:
обобщение и систематизация, расширение и углубление знаний о множестве чисел, обретение практических навыков при выполнении тренировочных заданий, привитие устойчивого интереса к математике, повышение уровня математической подготовки школьников; увеличение количества учащихся, для которых математика станет профессионально значимым предметом.
Задачи курса:
· сформировать у учащихся логическое представление о числах; > восполнить пробелы в знаниях о числах;
· сформировать навыки применения данных знаний при решении разнообразных задач различной сложности;
· сформировать навыки самостоятельной работы;
· сформировать умения и навыки исследовательской работы, работы со справочной литературой, с компьютером;
· способствовать развитию алгоритмического мышления, воспитанию умений действовать по данному алгоритму;
· показать, что источник возникновения изучаемых понятий - реальный мир, что они возникли из практических потребностей людей;
· показать, что понятия не изолированы друг от друга, а представляют определённую систему знаний, все звенья которой находятся во взаимной связи;
· способствовать развитию творческого и логического мышления учащихся;
· способствовать формированию познавательного и устойчивого интереса к математике;
· пополнить исторические сведения;
· обеспечить условия для расцвета личности школьника с учётом возрастных особенностей;
· привить навыки работы в группах, выступать, вести переговоры, отстаивать свое мнение и интересы;
· подготовка учащихся к профильной школе.
Календарно – тематическое планирование.
№/№
|
Тема занятий.
|
Кол - во часов.
|
Дата проведения. |
Виды деятельности.
|
Оборудование.
|
1.
|
Натуральные и целые числа.
|
Зч.
|
1
|
Натуральные числа. Система счисления.
|
1ч.
|
Анкетирование, аукцион знаний, демонстр. презентации. |
Лист ответов, компьютер, программ. обеспечение. |
2
|
1ростые и составные числа. НОД (Алгоритм Евклида).
|
1ч.
|
Исследов. работа,
Работа со справочником, практикум.
|
Компьютер, программное обеспечение
|
3
|
Множество целых чисел. Самостоятельная работа.
|
1ч.
|
Беседа, работа со
справочником. Самостоят. проверочная работа
|
Компьютер, программное обеспечение. Лист ответов.
|
2.
|
Рациональные числа.
|
1ч.
|
1
|
Обыкновенные и десятичные дроби. Периодические дроби. -
|
1ч.
|
Исследов. работа.
Работа со справочником, практикум.
|
Компьютер, программное обеспе-ние .
|
3.
|
Действительные числа. |
Зч. |
1
|
Непериодические бесконечные десятичные дроби. Иррациональные числа. |
1ч.
|
1екция, аукцион знаний. |
Компьютер, программное обеспечение. |
2
|
Коредь 1с-й степени из действительного числа.
|
1ч.
|
Работа со справочником, практикум. |
Компьютер, программное обесп. |
3
|
Систематизацияное тестирование.
|
1ч. |
Самостоятельная работа. |
Компьютер, лист ответов. |
4.
|
Комплексные числа.
|
Зч.
|
1.
|
Алгебраическая форма комплексного числа. Действия с комплексными числами.
|
1ч.
|
Проблемная беседа Практикум. |
Компьютер, программное обссп. |
2.
|
Применение комплексного числа.
|
1ч.
|
Лекция. |
Компьютер, программное обесп. |
3.
|
Систематизационное тестирование.
|
1ч.
|
Самостоятельная работа. |
Компьютер, лисе ответов. |
5.
|
Круглый стол
|
2ч.
|
Вопросы - ответы.
Обсуждение. Анкетирование
|
Заготовленные
вопросы. Лист ответов.
|
Итого:
|
12ч.
|
Тест
Действительные числа
1. Обратить обыкновенную дробь в десятичную:
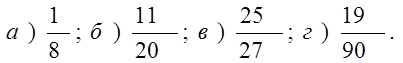
Ответ: а) 1) 0,102; 2) 0,125; 3) 0,1205.
б) 1) 0,55; 2)0,505; 3)0,255.
в) 1) 0,(925); 2) 0,9(25); 3) 0,92(5).
г) 1) 0;21; 2) 0,2(1); 3)0,(21).
2. Обратить десятичную дробь в обыкновенную:
а) 0,15; б) 0,225; в) 0,(6); г) 2,2(41).
Ответ: а) 1) 3/20; 2) 4/17; 3) 3/5.
б) 1) 9/40; 2) 2/19; 3) 1/40.
в) 1) 2/3; 2) 1/9; 3) 3/7.
г) 1) 2219/90; 2) 2219/990; 3)2219/999.
3)Выписать из данных чисел иррациональные:
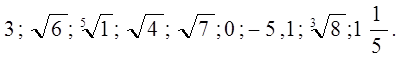
Ответ: а) 1) 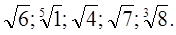
2) 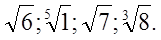
3) 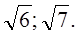
4. При каких х
имеет смысл выражение:
А. 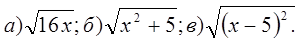
Ответ: а) 1) х>0
; 2) x
<0
; 3) x
- любые числа.
б) 1) х>5
; 2) x
<5
; 3) x
- любые числа.
в) 1) х ≥5
; 2) x
≤5
; 3) x
- любые числа.
Б.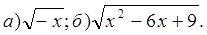
Ответ: а) 1) х ≥0
; 2) x
≤0
; 3) x
- любые числа.
б) 1) х ≥3
; 2) x
≤3
; 3) x
- любые числа.
5*
Упростить выражение:
Б.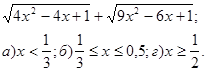
Ответ: а) 1) 2-5х
; 2) 5х-2
; 3) x
;
б) 1) 5х-2
;2) 2-5х
; 3)x
;
в) 1) 2-5х
;2) x
; 3) 5х-2
;
В.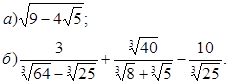
Ответ: а)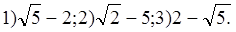
б) 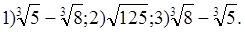
Тест
Комплексные числа.
1. Изобразить комплексные числа на координатной оси: z1
=4-6i
;
z2
=3+i
;
z3
=-5i
;
z4
=4-0i
;
z5
=-1,5=3i
;
z1
=-2-8i
;
2. Для комплексных чисел z1
и z2
найти:
1)z1
+ z2
; 2)z2
- z1
; 3) z1
z2
; 4) z1
: z2
:
z1
= 5-3i
, z2
= -4+7i.
Ответ:1. а)z1
+ z2
=1+4i;
б)z1
+ z2
=4+i;
в)z1
+ z2
=2+3i;
2. а)z2
- z1
=9-10i;
б) z2
- z1
=-9+10i
; в)z2
- z1
= -9-10i
;
3. а)z1
z2
=-41+47i
; б) z1
z2
=-1-47i
; в)z1
z2
=1+
47i
;
4. а)z1
: z2
=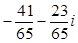 ; б) z1
: z2
= ; б) z1
: z2
=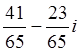 ; в) z1
: z2
= ; в) z1
: z2
=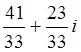 . .
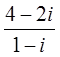 3. Составить квадратное уравнение с действительными коэффициентами, если известен один из его корней 3. Составить квадратное уравнение с действительными коэффициентами, если известен один из его корней
х1
=
Ответ: а) x2
-6x+10=0; б) x2
-6x+8=0; в) x2
+6x-10=0
4. Вычислить: 1)i21
,
2)i75
,
3)i44
Ответ: 1) а)i
; б)1; в)-
i
;
2) а)i
; б)1; в)-
i
;
3)а)i
; б)1; в)-
i
.
5. Выполнить действия:
1) (2+5i
)2
(3-i
);
2)*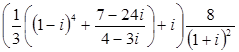
Ответ: 1. а)-43+81i
;
б)-83+81i
;
в)-23+39i
;
2. а)8i
;
б)0;
в)-4i
.
2.2. Планы-конспекты уроков
План-конспект №1. Тема урока: «Графический способ решения систем уравнений».
Цели урока:
· открыть совместно с учащимися новый способ решения систем уравнений, закрепить навыки построения графиков элементарных функций;
· формировать потребность приобретения новых знаний, создать условия для систематизации (самосистематизации) усвоения умений и навыков;
· развивать математическую речь при комментировании решения;
· воспитывать уважение друг к другу, взаимопонимание, уверенность в себе, развивать самостоятельность и творчество.
Ход урока.
Для урока мы используем следующую литературу: Учебник Ю.Н. Макарычева “Алгебра 9” под редакцией С.А. Теляковского., “Сборник задач для проведения письменного экзамена по алгебре за курс основной школы” “Дрофа” Москва 2001г., Материалы Единого Государственного Экзамена.
Во время урока учащийся ведет лист самосистематизации, где в ходе урока оценивает свое участие по 3-х бальной шкале (0,1,2).
1 – Самоопределение к деятельности. Организационный момент
Эпиграф
: Настоящий ученик умеет выводить известное из неизвестного и этим приближается к учителю (Гёте И.)
2 – Актуализация знаний и фиксация затруднений в деятельности.
А) Какие способы решения систем уравнений вы знаете?
Б) Решить систему уравнений (любым способом)
1. 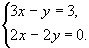 2. 2.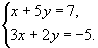 3. 3.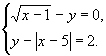
Решение системы №1:
Ответ (1,5;1,5)
Решение системы №2 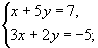
Ответ (-3;2)
Решение системы 3 вызывает у учащихся затруднение. Известными способами эту систему не решить.
3 - Постановка учебной задачи.
Учащиеся формулируют цель урока: “Научиться решать системы новым способом”
Вспоминаем недавно изученный графический способ решения уравнений. Нельзя ли его применить к решению систем. Вспомните определение графика уравнения с двумя переменными.
Работа устно:
С помощью каких преобразований можно построить графики данных элементарных функций.
А) 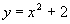
Б) 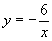
В) 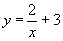
Г) 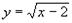
Д) 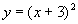
Е) 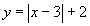
Ж) 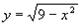
4 – Построение проекта выхода из затруднений.
Совместное создание алгоритма решения систем:
1. выразить переменную У через Х (если возможно);
2. построить график каждого уравнения;
3. найти координаты точки пересечения графиков.
Координаты любой точки построенного графика являются решением уравнения, следовательно, координаты каждой точки пересечения являются решением системы уравнений.
На доске учащиеся решают систему №3
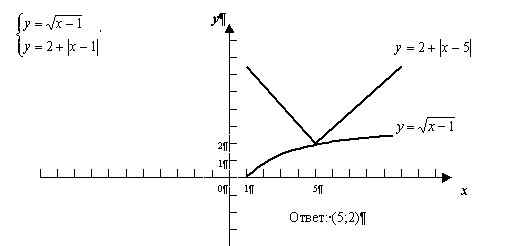
5 – Первичное закрепление (работа у доски по учебнику)
Решить графически систему уравнений
№233 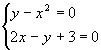
Решение:
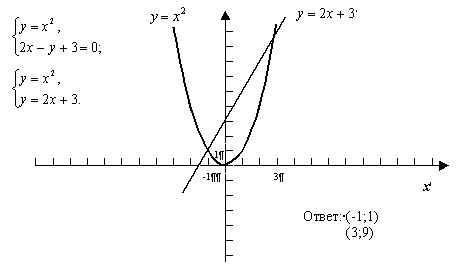
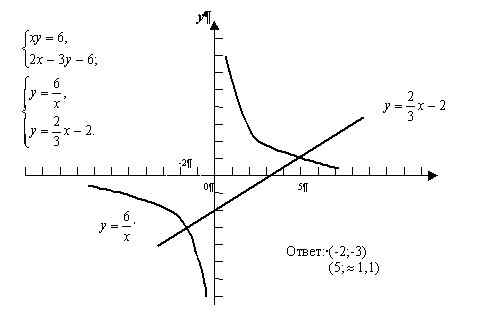
С помощью графиков решите систему уравнений
№236 а 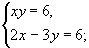
Решение:
Физ. Минутка.
(ведет физорг или валеолог класса).
Самостоятельная работа с самопроверкой. По вариантам. Упражнения взяты из “Сборника заданий для проведения экзамена по алгебре за курс основной школы”
1) Решите графически систему.
1 вар. №203 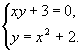 2 вар. №206 2 вар. №206 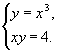
2) С помощью графиков определите: сколько решений имеет система уравнений
1 вар. 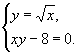 2 вар. 2 вар. 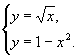
Решение №203 – 1 вариант.
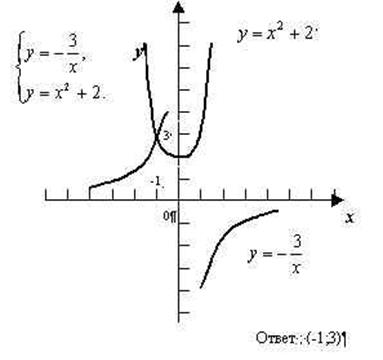
Решение №206 вариант 1
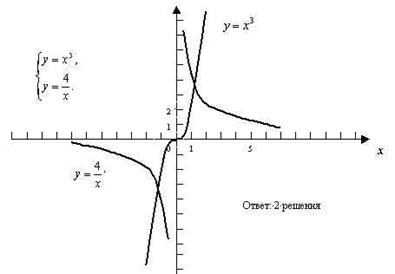
№203 вариант 2
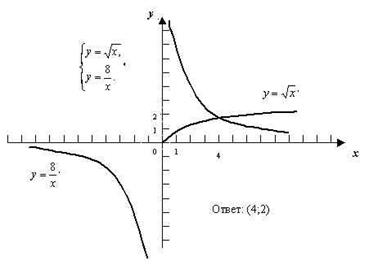
№206 вариант 2:
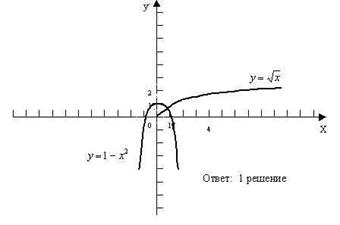
В конце работы выявляются причины ошибок или затруднений.
Работа творческого характера (по группам).
1. Решить систему
2. По готовому рисунку составить систему.
Учащиеся оценивают свое участие в работе групп.
Систематизация знаний:
1. Что нового вы узнали на уроке?
2. Достигли ли вы, поставленной в начале урока, цели?
3. Какую цель вы для себя ставите на следующем уроке?
В конце урока учащиеся сдают листы самооценки учителю.
Домашнее задание: № 302, № 304 или №305.
План-конспект №2. Компьютерные технологии на уроке математики в 9-м классе
Из классической педагогической литературы известно, что наиболее эффективной является такая организация учебного процесса, при которой максимально стимулируются творческие способности учащихся, и используются возможности новых информационных технологий обучения в организации внутреннего диалога учащихся на основе мультимодального взаимодействия.
Урок проходит в кабинете математики, оборудованном компьютерами, связанными локальной сетью в 9 классе с углубленным изучением математики, в котором учащиеся занимаются по подгруппам.
Тема:
Метод замены переменной в уравнениях. Исследование структуры уравнений приводимых к квадратным. (2 часа).
1-й час – исследование уравнений высших степеней, имеющих более сложную структуру, чем те, которые изучались в восьмом классе.
2-й час – урок-практикум - решения задач.
Цели
:
1) выработать умение учащихся видеть структуру уравнений и выбирать наиболее эффективно замену переменных для их решения на основе анализа коэффициентов уравнения;
2) расширить круг приемов решения уравнений, приводимых к квадратным;
3) углубить теоретические основы подхода к решению уравнений;
4) развить навыки работы с информационными технологиями;
5) активизировать интеллектуальную деятельность учащихся.
Задачи:
1) распознавание уравнений, приводимых к квадратным;
2) обоснование выбора подходящей замены переменных;
3) отработка навыков решения подобных уравнений;
4) повторение способов решения различных типов уравнений, сводящихся к квадратным;
5) развитие умения самостоятельно осуществлять небольшие исследования;
6) тренировка умения работы с электронными учебно-методическими материалами.
Схема урока
.
I.
Повторение пройденного материала и вопросов, подготавливающих к пониманию новых задач.
II.
1) Методы решения квадратных уравнений:
а) формула корней квадратного трехчлена;
б) выделение полного квадрата;
в) использование теоремы, обратной теореме Виета;
г) разложение на множители;
2) теоретические положения о количестве корней квадратного трехчлена;
3) теоремы о тождественных преобразованиях и равносильности уравнений;
4) метод замены переменной в биквадратных уравнениях.
Форма проведения урока – сочетание объяснения учителя с фронтальной коллективной работой учащихся.
III. Восприятие и первичное осознание нового материала, осмысление связей и отношений в объектах изучения.
Исследование структуры и решение уравнений, сводящихся к квадратным, на следующих примерах:
Объяснение учителя.
1) 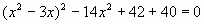 ; ;
2) 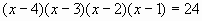 ; ;
3) 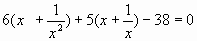 . .
Далее №№9.15(а); 9.16(а); 923(а) - решаются учащимися на доске.
Применение учащимися приобретенных знаний в самостоятельном выполнении задания по выбору подходящей замены переменной в решении уравнений, приводимые к квадратным.
Каждый ученик имеет свое рабочее место за персональным компьютером, на котором он получает свой вариант задания, сгенерированный компьютером по числу учеников по образцу подобранному учителем, решает и вводит с клавиатуры свой ответ.
Систематизация и обобщение знаний: После окончания выполнения задания компьютер проверяет ответ и выставляет оценку. В случае удовлетворительной (или неудовлетворительной) оценки ученик имеет возможность изучить правильное решение, запросив на компьютере соответствующую опцию, просмотреть правильное решение и выявить допущенные ошибки. Полученные оценки выставляются учителем в журнал.
IV.
Образец вариант задания, получаемого учащимися на этом уроке:
1) 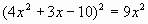 ; ;
2) 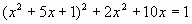 ; ;
3) 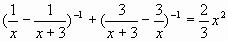 . .
Домашнее задание:
№№ 9.14(в, г), 9.16(б, г), 9.23(в, г).
М.А. Галицкий, А.М. Гольдман, Л.И. Звавич “Сборник задач по алгебре” 8 – 9 класс.
2.3. Результаты эксперимента
Цель: Изучитьуровень систематизации и обобщения полученных знаний на завершающем этапе эксперимента.
Для выявления влияния эксперимента, проведенного с детьми экспериментальной группы, мы провели эксперимент с учащимися систематизационной и экспериментальной групп. При этом использовались те же методики, что и в констатирующем эксперименте.
Таблица 1
Данные экспериментального изучения уровня систематизации и обобщения полученных знаний
| Контрольная группа |
Экспериментальная группа |
| Учащийся, № |
Количество правильных ответов |
Учащийся, № |
Количество правильных ответов |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
7
5
5
5
3
3
3
5
3
5
3
3
3
3
3
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
8
6
5
6
7
4
5
4
5
3
3
3
4
3
3
|
По данным таблицы мы получили следующие результаты:
· учащихся с высоким уровнем в контрольной группе 1 человек, в экспериментальной группе – 2 человека;
· количество учащихся со средним уровнем в контрольной группе 5 человек, в экспериментальной – 8 человек;
· учащихся с низким уровнем в контрольной группе 9 человек, в экспериментальной – 5 человек.
Контрольная группа:
F / N * 100%,
1/15*100% = 6,7%
5/15*100% = 33,3%
9/15*100% = 60%
Экспериментальная группа:
F / N * 100%,
2/15*100% = 13,3%
8/15*100% = 53,3%
5/15*100% = 33,4%
Результаты опроса представлены на рисунке 1.
Рис. 1. Выявление уровня систематизации и обобщения полученных знаний на стадии контрольного эксперимента по теме
«Алгебраические уравнения», 9 класс.
Из полученных данных мы видим, что высокий уровень составил в контрольной группе 6,7%, в экспериментальной – 13,3%. Средний уровень в контрольной группе – 33,3%, в экспериментальной – 53,3%, низкий уровень в контрольной группе 60%, в экспериментальной – 33,3%.
Таким образом, подводя итоги опроса, мы можем сделать вывод о том, что, говоря о систематизации и обобщении полученных математических знаний можно констатировать, что данный опрос показал, у учащихся 9 классов повысился уровень знаний по сравнению с итогами констатирующего эксперимента. Но, если сравнивать уровень знаний в контрольной и экспериментальной группах, то мы можем утверждать, что в экспериментальной группе уровень намного выше. Это было достигнуто благодаря использованию в нашем исследовании специализированных интегрированных уроков.
Таблица 2
Данные экспериментального изучения уровня сформированности знаний в контрольном эксперименте.
| Контрольная группа |
Экспериментальная группа |
| Учащийся, № |
Количество правильных ответов |
Учащийся, № |
Количество правильных ответов |
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
6
4
3
4
4
7
5
2
3
4
2
2
3
1
2
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
7
6
5
7
5
3
5
8
5
3
3
3
5
4
4
|
По данным таблицы мы получили следующие результаты:
· учащихся с высоким уровнем в контрольной группе 1 человек, в экспериментальной группе – 3 человека;
· количество учащихся со средним уровнем в контрольной группе 6 человек, в экспериментальной – 8 человек;
· учащихся с низким уровнем в контрольной группе 8 человек, в экспериментальной – 4 человека.
Контрольная группа:
F / N * 100%,
1/15*100% = 6,7%
6/15*100% = 40%
8/15*100% = 53,3%
Экспериментальная группа:
F / N * 100%,
3/15*100% = 20%
8/15*100% = 53,3%
4/15*100% = 26,7%
Результаты опроса представлены на рисунке 2.
Рис. 2. Выявление уровня математических знаний учащихся на стадии контрольного эксперимента
Из полученных данных мы видим, что высокий уровень составил в контрольной группе 6,7%, в экспериментальной – 20%. Средний уровень в контрольной группе – 40%, в экспериментальной – 53,3%, низкий уровень в контрольной группе 53,3%, в экспериментальной – 26,7%.
Итак, анализ данных контрольного эксперимента показал, что уровень знаний возрос в обеих группах по сравнению с результатами констатирующего эксперимента. Но, если сравнивать показатели знаний в контрольной и экспериментальной группах, то уровень знаний в экспериментальной группе намного выше уровня знаний контрольной группы. Это стало возможным при использовании интегрированного урока.
Таким образом, проведенные нами исследования свидетельствуют о том, что, если систематически использовать такие формы систематизации и обобщения на уроках математики, как математический диктант, контрольные работы, а также проводить специализированные уроки, то:
· расширяются и систематизируются представления школьников по предмету;
· формируются навыки самосистематизации и обобщения знаний.
Заключение
Систематизация и обобщение знаний и умений учащихся – одно из основных условий повышения качества обучения. Учитель математики в своей работе должен использовать не только общепринятые формы систематизации (самостоятельная и систематизационная работы, устный опрос у доски и т.д.), но и постоянно изобретать, внедрять свои средства систематизации. Умелое владение учителем различными формами систематизации знаний и умений способствует повышению заинтересованности учащихся в изучении предмета, предупреждает отставание, обеспечивает активную работу каждого ученика. Систематизация для учащихся должна быть обучающей.
В результате проведения нетрадиционных форм систематизации знаний и умений раскрываются индивидуальные особенности детей, повышается уровень подготовки к уроку, что позволяет своевременно устранять недостатки и пробелы в знаниях учащихся.
Список литературы
1. Амонашвили Ш. А. Обучение. Оценка. Отметки. – М.: Знание, 2004.
2. Баймуханов Б. Б. Тематический контроль и учет знаний // Математика в школе, 2006. - №5.
3. Борода Л.Я. Некоторые формы систематизации знаний на уроке // Математика в школе, 2005. - №4.
4. Вахламова А. П., Рабунский Е. С. О систематической взаимопроверке знаний учащихся на уроках // Математика в школе, 2004. - №1.
5. Груденов Я. И. Совершенствование методики работы учителя математики – М: Просвещение, 2005.
6. Дакацьян У. В. Проверка знаний учащихся по математике – М.: Академия, 2005.
7. Денищева Л. О., Кузнецова Л. В., Лурье И.А. и др. Зачеты в системе дифференцированного обучения математики – М: Просвещение, 2003.
9. Зив Б. Г. Задачи к урокам алгебры: 7-11 кл. – М.: Русское слово, 2003.
10. Ильина Т. А. Педагогика: курс лекций: учебное пособие для студентов пед. ин-тов.– М: Просвещение, 2004.
11. Калинина М.И. К вопросу о систематизации знаний учащихся/ сб. статей, сост. Борчугова З. Г., Батий Ю. Ю. – М.: Просвещение, 2004.
12. Колобова Е. В. Использование зачетной системы для контроля и оценки знаний учащихся // Математика в школе , 2004. - №3.
13. Качество знаний учащихся и пути его совершенствования / Под ред. Скаткина М.Н., Краевского М.Н. – М.: Педагогика, 2003.
14. О совершенствовании методов обучения математики / Сб. статей сост. Крамор В. С. – М.: Просвещение, 2004.
15. МПМ в средней школе. Частная методика / Сост. Мишин В. И. – М: Просвещение, 2003.
16. Петровский Е. И. Проверка и оценка знаний учащихся – М.: АПН РФ, 2005.
18. Планирование обязательных результатов обучения математике / сост. В. В. Фирсов – М.: Просвещение, 2002.
19. Программы общеобразовательных учреждений. Математика – М: Просвещение, 2006.
21. Скобелев Г. Н. Систематизация знаний на уроках математики – Минск, 2006.
22. Современные основы школьного курса математики. / Н. Я. Виленкин, К. И. Дудничев, Л. А. Калужнин, А. А. Столяр. – М.: Просвещение, 2004.
23. Утеева Р. А. Групповая работа как одна из форм деятельности учащихся на уроке // Математика в школе, 2005. - №2.
24. Харламов И. Ф. Педагогика. Курс лекций. – Минск, 2005.
25. Шаталов В. Ф. Куда и как исчезли тройки – М.: Педагогика, 2004.
|