ПЕДАГОГІЧНА ПРАКТИКА
Розробка учбового матеріалу для викладання вищої математики
на тему
"Наближені методи обчислення визначених інтегралів"
Зміст
Вступ
1. Постановка задачі наближеного інтегрування
2. Чисельні методи інтегрування
2.1 Метод прямокутників
2.2 Метод трапецій
2.3 Метод Симпсона
2.4 Практичне порівняння точності методів наближеного обчислення інтегралів 3-ма методами
3. Графічне інтегрування
Список використаної літератури
Актуальність теми контрольної роботи полягає в тому, щопри розв’язанні низки математичних, фізичних або технічних задач застосовуються визначені інтеграли від функцій, первісні функції яких не виражаються через елементарні функції. Крім того, в окремих задачах доводиться мати справу з визначеними інтегралами, у яких самі підінтегральні функції не являються елементарними. Це приводить до необхідності розробки наближених методів обчислення визначених інтегралів.
Об’єктом роботи є визначені інтеграли, які не можуть бути представлені у вигляді комплексу елементарних функцій.
Предметом роботи є методи наближеного обчислення визначених інтегралів, первісна яких не може бути представлена у вигляді комплексу елементарних функцій.
Метою роботи є аналіз умов використання та оцінки похибок обчислень при застосуванні найбільш уживаних методів наближеного обчислення визначених інтегралів:
метод прямокутників;
метод трапецій;
метод Симпсона або метод парабол;
методів графічного інтегрування.
Інформаційною базою досліджень контрольної роботи є математичні монографії та учбові посібники з вищої математики по курсу „Методи обчислень" з взяттям за основу курсу учбового посібника Бойко Л.Т. „Основи чисельних методів: навч. посібник." - Дніпропетровськ: Вид-во ДНУ, 2009.
Під чисельним інтегруванням розуміють наближене обчислення визначених інтегралів.
Якщо для функції 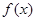 , визначеної на відрізку , визначеної на відрізку 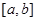 , можно знайти первісну функцію , можно знайти первісну функцію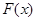 , то визначений інтеграл розраховується за формулою функціонального інтегрування (1.1) [6]: , то визначений інтеграл розраховується за формулою функціонального інтегрування (1.1) [6]:
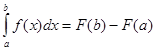 (1.1) (1.1)
Якщо підінтегральна функція 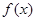 має складний аналітичний вираз, або задана таблично, то звичайні методи інтегрування, які вивчаються в математичному аналізі, непридатні, оскільки неможливо побудувати первісну. Тому доводиться обчислювати інтеграли наближено. Формули наближеного обчислення інтегралів називаються квадратурними формулами. Ці формули міняють оператор інтегрування на оператор сумування. Виникаюча при такій заміні похибка називається похибкою квадратурної формули. має складний аналітичний вираз, або задана таблично, то звичайні методи інтегрування, які вивчаються в математичному аналізі, непридатні, оскільки неможливо побудувати первісну. Тому доводиться обчислювати інтеграли наближено. Формули наближеного обчислення інтегралів називаються квадратурними формулами. Ці формули міняють оператор інтегрування на оператор сумування. Виникаюча при такій заміні похибка називається похибкою квадратурної формули.
Реклама

Задача чисельного інтегрування функцій полягає в обчисленні визначеного інтеграла за значеннями інтегруємої функції в ряді точок відрізка інтегрування. Функцію 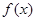 заміняємо інтерполюємою функцією заміняємо інтерполюємою функцією 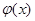 , а потім приблизно припускаємо [4]: , а потім приблизно припускаємо [4]:
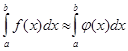 (1.2) (1.2)
Функція 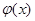 повинна бути такою, щоб інтеграл повинна бути такою, щоб інтеграл 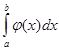 обчислювався безпосередньо. Якщо обчислювався безпосередньо. Якщо 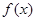 задана аналітично, то ставимо питання про оцінку похибки формули (1.2). задана аналітично, то ставимо питання про оцінку похибки формули (1.2).
В загальному вигляді задача чисельного інтегрування може бути викладена наступним чином [1]. Нехай інтеграл, який потрібно визначити, представлено у вигляді
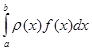 (1.3) (1.3)
Підінтегральна функція в формулі (1.3) є такою, що не дозволяє в функціональному вигляді отримати первісну функцію.
Цей інтеграл обчислюємо за наближеною квадратурною формулою:
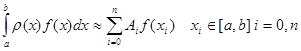 (1.4) (1.4)
де: функція 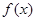 - визначена і неперервна на інтервалі - визначена і неперервна на інтервалі 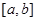 ; ;
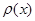 - вагова функція, яка може мати якісь особливості на відрізку - вагова функція, яка може мати якісь особливості на відрізку
інтегрування, наприклад, перетворюватись у нескінченість в
деяких точках цього відрізка.
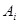 - квадратурні коефіцієнти; - квадратурні коефіцієнти;
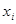 - квадратурні вузли ( - квадратурні вузли (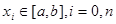 ); );
n - довільне число інтервалів всередині відрізку [a,b].
Сума, що стоїть у правій частині наближеної рівності (1.4), називається квадратурною сумою.
Параметри 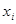 , ,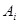 вибирають так, щоб або похибка квадратурної формули була по можливості мінімальною, або обчислення за формулою (1.4) були достатньо простими. Різні квадратурні формули відрізняються одна від одної способами вибору параметрів вибирають так, щоб або похибка квадратурної формули була по можливості мінімальною, або обчислення за формулою (1.4) були достатньо простими. Різні квадратурні формули відрізняються одна від одної способами вибору параметрів 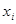 , ,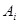 . .
Більшість квадратурних формул базується на заміні підінтегральної функції 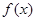 алгебраїчними багаточленами різного степеня. алгебраїчними багаточленами різного степеня.
Означення: Кажуть, що квадратурна формула (1.4) має алгебраїчний степінь точності 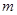 , якщо ця наближена формула стає точною на множині всіх алгебраїчних багаточленів не вище , якщо ця наближена формула стає точною на множині всіх алгебраїчних багаточленів не вище 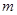 -ого степеня. -ого степеня.
Це означає, що якщо до наближеної формули (1.4) замість функції 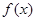 підставити будь-який алгебраїчний багаточлен підставити будь-який алгебраїчний багаточлен 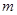 -ого степеня, то наближена рівність (1.4) стає точною, тобто -ого степеня, то наближена рівність (1.4) стає точною, тобто
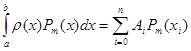 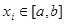 (1.5) (1.5)
Але при цьому наближена рівність (1.4) не для всіх багаточленів степеня 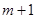 буде точною. буде точною.
Алгебраїчний степінь точності квадратурної формули є мірою точності цієї формули. Оскільки будь-яку неперервну функцію 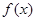 можна як завгодно точно наблизити алгебраїчними багаточленами (за рахунок збільшення степеня багаточлена), то слід очікувати, що квадратурні формули, які мають високий алгебраїчний ступінь точності, будуть мати високу точність для будь-яких неперервних функцій можна як завгодно точно наблизити алгебраїчними багаточленами (за рахунок збільшення степеня багаточлена), то слід очікувати, що квадратурні формули, які мають високий алгебраїчний ступінь точності, будуть мати високу точність для будь-яких неперервних функцій 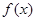 . .
Реклама

Параметри 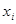 , ,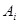 можна вибрати так. щоб зробити алгебраїчний ступінь точності квадратурної формули якомога вищим. Такі формули називаються квадратурними формулами найвищого степеня точності. Вперше вони були розглянуті Гауссом і тому їх часто називають формулами гауссового типу. можна вибрати так. щоб зробити алгебраїчний ступінь точності квадратурної формули якомога вищим. Такі формули називаються квадратурними формулами найвищого степеня точності. Вперше вони були розглянуті Гауссом і тому їх часто називають формулами гауссового типу.
Якщо вузли 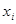 вибрати з міркувань зручності (рівномірно розташованими вибрати з міркувань зручності (рівномірно розташованими 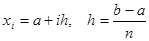 ,), а коефіцієнти ,), а коефіцієнти 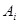 - з міркувань точності, то у випадку - з міркувань точності, то у випадку  отримаємо квадратурні формули Ньютона - Котеса [2]. отримаємо квадратурні формули Ньютона - Котеса [2].
Якщо вузли 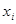 вибрати з міркувань точності, а коефіцієнти вибрати з міркувань точності, а коефіцієнти 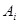 - з міркувань зручності (всі коефіцієнти однакові), то добудемо квадратурні формули, що носять ім’я Чебишова [2]. - з міркувань зручності (всі коефіцієнти однакові), то добудемо квадратурні формули, що носять ім’я Чебишова [2].
Обгрунтування інтерполяційних квадратурних формул будується на наступних висновках [1].
Нехай на відрізку інтегрування якось зафіксовані різні між собою вузли 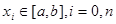 , і будемо вибирати лише коефіцієнти , і будемо вибирати лише коефіцієнти 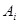 ( (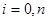 ) так, щоб формула (1.4) була якомога точнішою. Припускаємо, ) так, щоб формула (1.4) була якомога точнішою. Припускаємо, 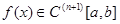 , тобто функія , тобто функія 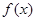 і всі її похідні до і всі її похідні до 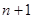 порядку включно є неперервними на відрізку порядку включно є неперервними на відрізку 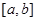 . Візьмемо квадратурні вузли як вузли інтерполяції (оскільки вони всі з відрізку інтегрування та всі різні між собою), та побудуємо інтерполяційний багаточлен . Візьмемо квадратурні вузли як вузли інтерполяції (оскільки вони всі з відрізку інтегрування та всі різні між собою), та побудуємо інтерполяційний багаточлен 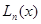 для функції для функції 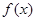 . Будемо мати таку рівність . Будемо мати таку рівність
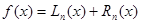 (1.5) (1.5)
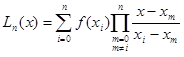 (1.6) (1.6)
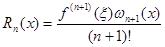 (1.7) (1.7)
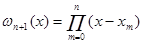 (1.8) (1.8)
Розглянемо тепер інтеграл від функції 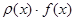 
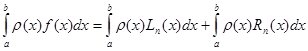 (1.9) (1.9)
підставимо (1.6), (1.7), (1,8) до формули (1.9)
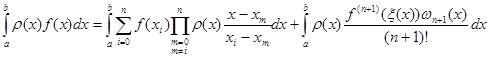 (1.10) (1.10)
Якщо позначити
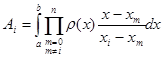 (1.11) (1.11)
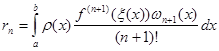 (1.12) (1.12)
то інтеграл (1.10) можна переписати у вигляді
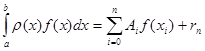 (
1.13)
(
1.13)
Відкинувши у (1.13) похибку 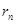 , добудемо наближену формулу (1.4). , добудемо наближену формулу (1.4).
Означення. Квадратурна формула (1.4) будемо називати інтерполяційною, якщо квадратурні коефіцієнти 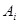 , ,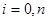 визначаються формулами (1.11). Нагадаємо, що квадратурні вузли при цьому всі різні та всі розташовані на відрізку інтегрування, в усьому іншому вони довільні. визначаються формулами (1.11). Нагадаємо, що квадратурні вузли при цьому всі різні та всі розташовані на відрізку інтегрування, в усьому іншому вони довільні.
Формула (1.12) визначає похибку інтерполяційної квадратурної формули. З похибки видно, що алгебраїчний степінь точності інтерполяційної квадратурної формули дорівнює 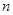 . Збільшити степінь точності можна лише за рахунок вибору вузлів . Збільшити степінь точності можна лише за рахунок вибору вузлів 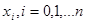 . .
Квадратурні формули при сталій ваговій функції та з рівновіддаленими вузлами називають формулами Ньютона-Котеса у пам’ять того, що вперше вони в достатньому загальному вигляді були розглянуті Ньютоном, коефіцієнти вперше були добуті Котесом  [4]. [4].
Кінечний відрізок інтегрування 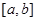 ділимо на ділимо на 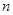 рівних частин довжини рівних частин довжини 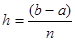 , точки ділення беремо за вузли інтерполяційної формули. Спростимо вигляд квадратурних коефіцієнтів , точки ділення беремо за вузли інтерполяційної формули. Спростимо вигляд квадратурних коефіцієнтів 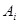 , ,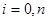 , які визначаються формулою (1.11), підставивши туди , які визначаються формулою (1.11), підставивши туди
 , ,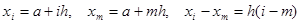 . .
Крім того перейдемо до нової змінної інтегрування 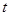 , де , де 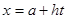
Для виконання всіх цих дій спочатку розглянемо добуток у формулі (1.11)
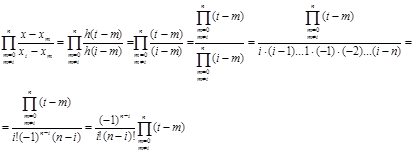 (1.14) (1.14)
Підставимо добуток (1.14) до формули (1.11) та перейдемо до нової змінної, будемо мати
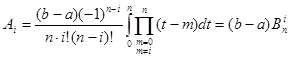 (1.15) (1.15)
Де
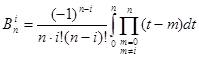 (1.16) (1.16)
Квадратурна формула Ньютона-Котеса приймає вигляд
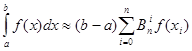 (1.17) (1.17)
Алгебраїчна степінь точності формули (1.17) дорівнює 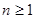 . Коефіцієнти (1.16) називаються коефіцієнтами Котеса. Вони мають властивості: . Коефіцієнти (1.16) називаються коефіцієнтами Котеса. Вони мають властивості:
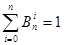 . Дійсно, підставимо до формули (1.17) . Дійсно, підставимо до формули (1.17) 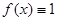 , тоді , тоді 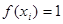 , при цьому наближена формула стає точною. Виконуємо інтегрування властивість доведена. , при цьому наближена формула стає точною. Виконуємо інтегрування властивість доведена.
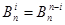 , тобто рівновіддалені від кінців коефіцієнти формули Ньютона -Котеса є однаковими. Дійсно, маємо з формули (1.16) , тобто рівновіддалені від кінців коефіцієнти формули Ньютона -Котеса є однаковими. Дійсно, маємо з формули (1.16)
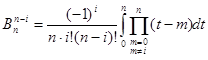
Зробимо заміну змінної інтегрування 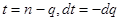 тоді тоді
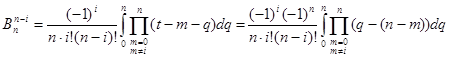
В добутку перейдемо до нового індексу 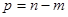 і властивість доведена і властивість доведена
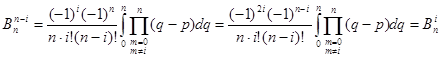
3. Коефіцієнти 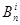 не залежать від довжини відрізка інтегрування та підінтегральної функції не залежать від довжини відрізка інтегрування та підінтегральної функції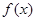 , тому вони можуть бути обчислені раз і назавжди , тому вони можуть бути обчислені раз і назавжди
В залежності від вибраного параметра n отримана загальна форма квадратурних рівнянь розподіляється на випадки [6]:
1) Коли 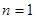 , то застосовуєма форма квадратурних рівнянь називається - „квадратурна формула трапеції”; , то застосовуєма форма квадратурних рівнянь називається - „квадратурна формула трапеції”;
2) Коли 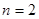 , то застосовуєма форма квадратурних рівнянь називається - „квадратурна формула Симпсона”; , то застосовуєма форма квадратурних рівнянь називається - „квадратурна формула Симпсона”;
3) Коли 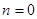 , формула (1.19) не застосовується, оскільки значення не визначені, тому застосовується особливий випадок „квадратурної формули прямокутників (ліві, праві, центральні) ". , формула (1.19) не застосовується, оскільки значення не визначені, тому застосовується особливий випадок „квадратурної формули прямокутників (ліві, праві, центральні) ".
Нехай є відрізок 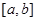 і нам треба обчислити визначений інтеграл і нам треба обчислити визначений інтеграл
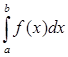 (
2.1 1)
(
2.1 1)
за попередньо представленою загальною квадратурною формулою Н’ютона - Котеса (1.4)
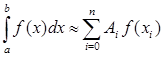 (
2.1 2)
(
2.1 2)
де 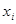 - деякі фіксовані вузли - деякі фіксовані вузли
Найпростіший варіант інтерполяційної квадратурної формули (2.1 2) виникає, коли 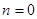 [1]. У цьому випадку не можна скористатися формулою (1.20), бо коефіцієнт (1.19) при [1]. У цьому випадку не можна скористатися формулою (1.20), бо коефіцієнт (1.19) при 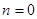 невизначений. Тому, як і при побудові загальної інтерполяційної формули, замінимо підінтегральну функцію інтерполяційним багаточленом нульового степеня, що побудований за єдиним вузлом невизначений. Тому, як і при побудові загальної інтерполяційної формули, замінимо підінтегральну функцію інтерполяційним багаточленом нульового степеня, що побудований за єдиним вузлом 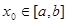 . .
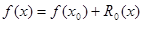 (2.1 3) (2.1 3)
при заміні підінтегральної функції (2.1 2) інтерполяційним поліномом нульового степеня, що побудований по єдиному вузлу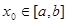
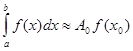 (
2.1 3)
(
2.1 3)
Знайдемо коефіціент 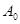
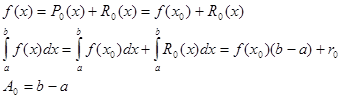 (2.1 4) (2.1 4)
Після інтегрування маємо квадратурну „формулу прямокутника”:
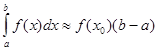 , ,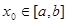 (2.1 5) (2.1 5)
При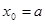 її називають формулою лівих прямокутників, її називають формулою лівих прямокутників,
При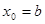 її називають формулою правих прямокутників, її називають формулою правих прямокутників,
При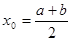 - центральних (або середніх) прямокутників. - центральних (або середніх) прямокутників.
Геометричне тлумачення цієї формули показано на рис 2.1
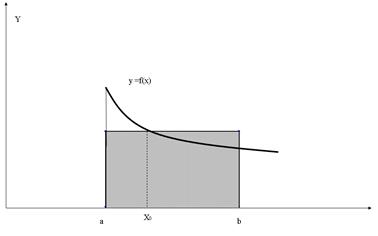
Рис.2.1 Геометричне зображення „формули прямокутників"
Оцінимо похибку 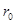 квадратурної формули (2.1 5) за умови, що квадратурної формули (2.1 5) за умови, що 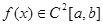 . За означенням похибки квадратурної формули (2.1 5) маємо . За означенням похибки квадратурної формули (2.1 5) маємо
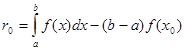 (2.1 6) (2.1 6)
Функцію 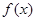 запишемо у вигляді розвинення в ряд Тейлора в околі точки запишемо у вигляді розвинення в ряд Тейлора в околі точки 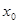 [7]: [7]:
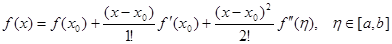 (2.1 7) (2.1 7)
Проінтегруємо обидві частини рівності (2.1 7) по відрізку 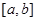
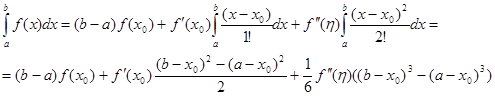 (2.1 8) (2.1 8)
Тепер підставимо інтеграл (2.1 8) в (2.1 6)
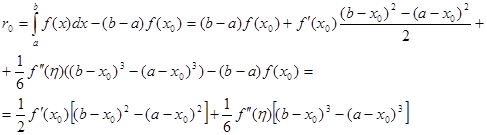
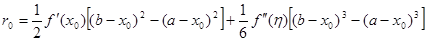 (2.1 9) (2.1 9)
Тепер розглянемо конкретні варіанти вибору точки 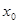
При 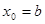 (праві прямокутники): (праві прямокутники): 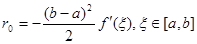 (2.1 10) (2.1 10)
При 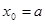 (ліві прямокутники): (ліві прямокутники): 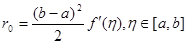 (2.1 11) (2.1 11)
При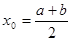 - (центральні прямокутники): - (центральні прямокутники): 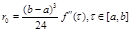 (2.1 12) (2.1 12)
З формул (2.1 10), (2.1 11), (2.1 12) видно, що алгебраїчний степінь точності формули центральних прямокутників на 1 вище ніж лівих або правих.
Якщо довжина відрізку 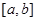 велика, то формули прямокутників мають невисоку точність. У цих випадках краще користуватися сумарними формулами прямокутників. Для цього розіб‘ємо відрізок на велика, то формули прямокутників мають невисоку точність. У цих випадках краще користуватися сумарними формулами прямокутників. Для цього розіб‘ємо відрізок на 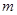 рівних частин з кроком рівних частин з кроком 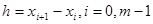 . Інтеграл шукаємо як суму інтегралів по всіх цих відрізках, тобто . Інтеграл шукаємо як суму інтегралів по всіх цих відрізках, тобто
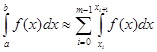 (2.1 13) (2.1 13)
На кожному відрізку 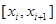 інтеграл обчислюємо, користуючись однією з квадратурних формул прямокутників. Розглянемо окремі випадки. інтеграл обчислюємо, користуючись однією з квадратурних формул прямокутників. Розглянемо окремі випадки.
1. „Ліві прямокутники"
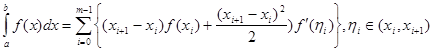 . (2.1 14) . (2.1 14)
В останній формулі (2.1 14) враховано не тільки наближені значення інтегралів за формулою (2.1 5), але й залишки за формулою (2.1 9). Тепер в правій частині цієї рівності запишемо окремо суму наближених значень інтегралів та суму залишків
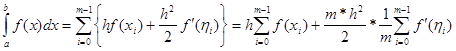 (2.1 15) (2.1 15)
Приймемо до уваги неперервності функції 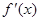 на на 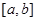 . Нехай . Нехай
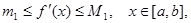
тоді існує така точка  ,
що буде вірною рівність
,
що буде вірною рівність 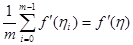
Тепер з формули (2.1 15) маємо остаточно узагальнену формулу „лівих прямокутників”:
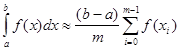 (2.1 16) (2.1 16)
та похибку цієї формули
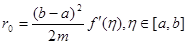 (2.1 17) (2.1 17)
Геометричне зображення „формули лівих прямокутників" наведене на рисунку (2.2)
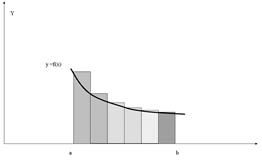
Рис.2.2 Геометричне зображення „формули лівих прямокутників"
2. Аналогічно для квадратурної формули „правих прямокутників" отримуємо узагальнену формулу
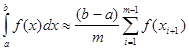 (2.1 18) (2.1 18)
та похибку
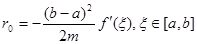 (2.1 19) (2.1 19)
Геометричне зображення „формули правих прямокутників" наведене на рисунку (2.3).
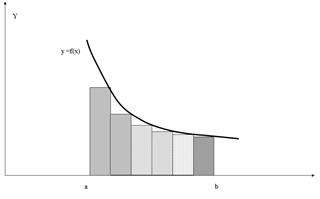
Рис.2.3 Геометричне зображення „формули правих прямокутників”
3. Узагальнена квадратурна формула „центральних прямокутників" запишеться у вигляді:
 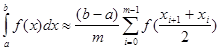 (2.1 20) (2.1 20)
її залишок має вигляд
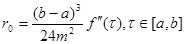 (2.1 21) (2.1 21)
Геометричне зображення „формули центральних прямокутників" наведене на рисунку (2.4).
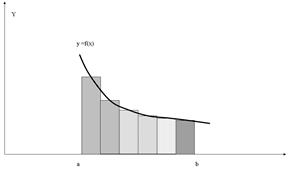
Рис.2.4 Геометричне зображення „формули центральних прямокутників"
Квадратурна „формула трапеції” - це виключний випадок формули Н’ютона - Котеса (1.20), коли 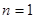 [1]. Квадратурна формула трапеції має вигляд: [1]. Квадратурна формула трапеції має вигляд:
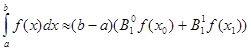 (2.2.1) (2.2.1)
Два коефіцієнти Котеса знаходимо, враховуючи їхні властивості
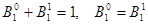
Тоді формула трапеції має вигляд
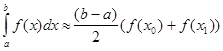 (2.2.2) (2.2.2)
Геометричне тлумачення наведене на рис.2.5 Геометрично цю формулу отримаємо, якщо криву 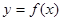 замінити хордою, яка проходить через точки замінити хордою, яка проходить через точки 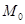 та та 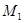 , тоді інтеграл знаходиться як площа трапеції , тоді інтеграл знаходиться як площа трапеції 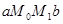 . .
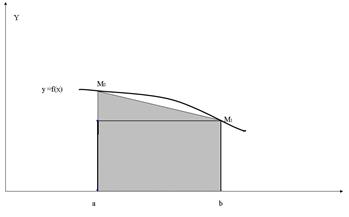
Рис.2.5 Геометричне тлумачення „формули трапецій”
Формула (2.2.2) наближена. Визначимо похибку для квадратурної формули трапеції:
Похибка квадратурної формули (2.2.2) випливає з (1.12), якщо взяти  та та 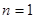
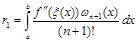
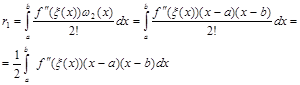
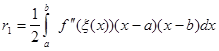 (2.2.3) (2.2.3)
До обчислення останнього інтеграла застосуємо теорему про середнє [5].
Теорема. Нехай 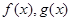 - інтегровані на проміжку - інтегровані на проміжку 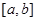 функції, причому функції, причому 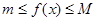 , , 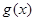 на всьому проміжку не змінює знак. Тоді на всьому проміжку не змінює знак. Тоді
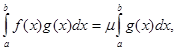 де де 
Якщо 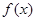 неперервна на неперервна на 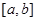 , то ця формула може бути записана у вигляді , то ця формула може бути записана у вигляді
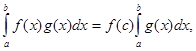 де де 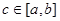
Застосуємо цю теорему до інтеграла (2.2.3). За припущенням функція 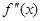 є неперервною на є неперервною на 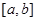 , тому знайдеться така точка , тому знайдеться така точка  , що буде виконуватися рівність. , що буде виконуватися рівність.
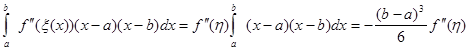
Отже,
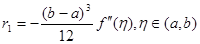 (2.2.4) (2.2.4)
Якщо відрізок 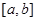 достатньо великий, то похибка (2.2.4) квадратурної формули трапеції, як правило, велика. Для збільшення точності розділимо відрізок інтегрування на достатньо великий, то похибка (2.2.4) квадратурної формули трапеції, як правило, велика. Для збільшення точності розділимо відрізок інтегрування на 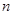 частин точками частин точками 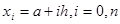 , тоді , тоді
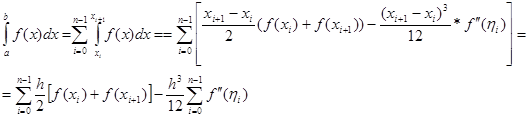
Якщо розбиття рівномірне, тобто 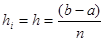 , то , то
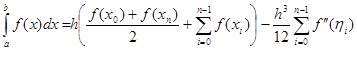
Запишемо окремо узагальнену формулу трапеції і окремо її похибку:
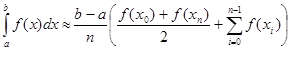 (2.2.5) (2.2.5)
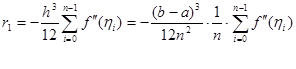 (2.2.6) (2.2.6)
Величина 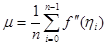 -середнє арифметичне значень другої похідної в -середнє арифметичне значень другої похідної в 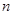 точках відрізку точках відрізку 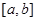 . Очевидно, що . Очевидно, що 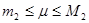 , де , де 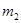 -найменше значення, а -найменше значення, а 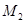 -найбільше значення другої похідної -найбільше значення другої похідної 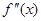 , , 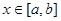 . Оскільки . Оскільки 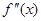 неперервна на неперервна на 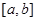 , то в якості своїх значень на , то в якості своїх значень на 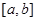 вона приймає всі проміжні числа між вона приймає всі проміжні числа між 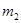 і і 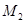 . Отже, існує така точка . Отже, існує така точка 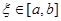 , що , що  , тобто , тобто
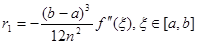 (2.2.7) (2.2.7)
На рис (2.6) показано геометричне зображення узагальненої формули трапеції (2.2.5).
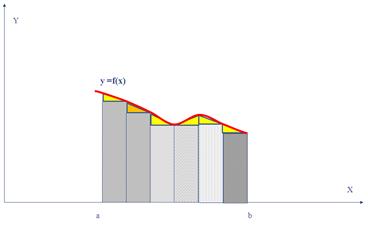
Рис.2.6 Геометричне зображення узагальненої формули трапецій
Точне значення інтеграла, тобто ліва частина наближеної рівності (2.2.5) це площа криволінійної трапеції, що обмежена зверху графіком функції 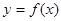 . Наближене значення інтеграла (права частина рівності (2.2.5) - це площа фігури, що зверху обмежена ламаною . Наближене значення інтеграла (права частина рівності (2.2.5) - це площа фігури, що зверху обмежена ламаною 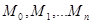 (рис.2.6). (рис.2.6).
З формули (2.2.7) видно, що чим більшим є число 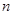 , тим меншою буде похибка квадратурної формули (2.2.5). Крім того, з (2.2.7) видно, що алгебраїчний степінь точності і квадратурної формули трапеції дорівнює одиниці (так же, як і формули центральних прямокутників). , тим меншою буде похибка квадратурної формули (2.2.5). Крім того, з (2.2.7) видно, що алгебраїчний степінь точності і квадратурної формули трапеції дорівнює одиниці (так же, як і формули центральних прямокутників).
Якщо в квадратурній формулі Ньютона-Котеса (2.12) взяти 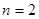 то здобудемо таку формулу [1] то здобудемо таку формулу [1]
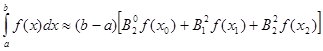 (2.3.1) (2.3.1)
За формулою (2.11) знаходимо 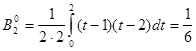 . Врахувавши властивості коефіцієнтів Котеса, знаходимо . Врахувавши властивості коефіцієнтів Котеса, знаходимо 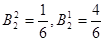 . .
Після підстановок знайдених коефіцієнтів Котеса в формулу (2.3.1), отримуємо квадратурну формулу, яка називається „формулою Симпсона” або „формулою парабол”:
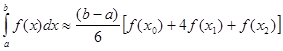 (2.3.2) (2.3.2)
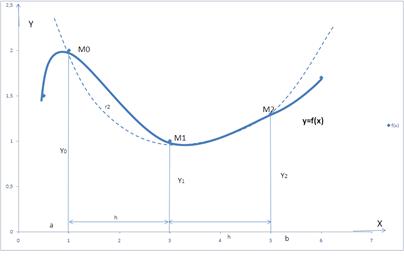
Рис.2.7 Геометричне тлумачення „формули парабол"
Назва квадратурної формули (2.3.2) як „формула парабол" випливає з геометричного тлумачення інтеграла, якщо криву 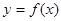 замінити параболою, що проходить через три точки замінити параболою, що проходить через три точки 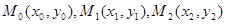 (на рис.2.7 парабола показана пунктиром) і наближене значення інтеграла обчислювати як площу криволінійної трапеції, яка зверху обмежена графіком цієї параболи. (на рис.2.7 парабола показана пунктиром) і наближене значення інтеграла обчислювати як площу криволінійної трапеції, яка зверху обмежена графіком цієї параболи.
Знайдемо залишковий член квадратурної формули Симпсона. Для цього з наближеної рівності (2.3.2) запишемо формулу для похибки
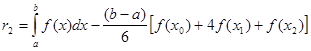 (2.3.3) (2.3.3)
Розкладемо функцію 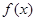 у ряд Тейлора в околі точки у ряд Тейлора в околі точки 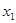 , припускаючи функцію , припускаючи функцію 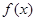 такою, що розкладання можливе [7]: такою, що розкладання можливе [7]:
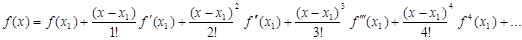
Знайдемо точне значення інтеграла:
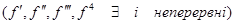
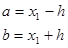
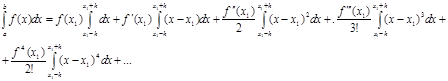
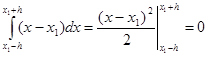
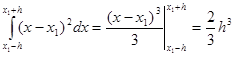
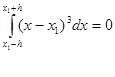
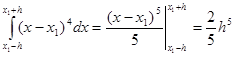
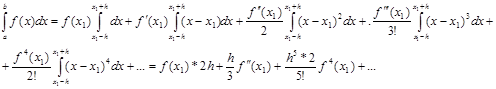
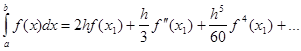 (2.3.4) (2.3.4)
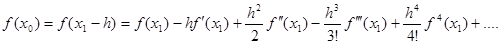
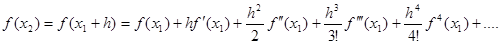
Тепер знаходимо
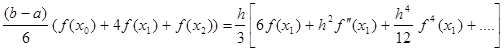 (
2.3.5)
(
2.3.5)
Підставимо (2.3.3) і (2.3.5) у праву частину рівності (2.3.4):
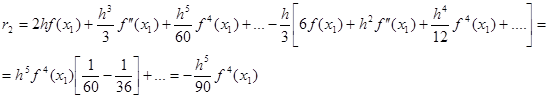
Отже похибка квадратурної формули Симпсона може бути записана у вигляді
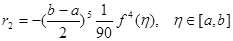 (2.3.6) (2.3.6)
З формули (2.3.6) видно, що алгебраїчний степінь точності квадратурної формули Симпсона дорівнює трьом, тобто ця формула має підвищений степінь точності.
Формулу Симпсона також можна застосовувати не до всього відрізка інтегрування, а до окремих його частин. Для цього поділимо відрізок 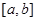 на на 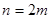 частин рівної довжини частин рівної довжини 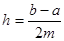 кожний, як показано на рисунку (2.8) кожний, як показано на рисунку (2.8)
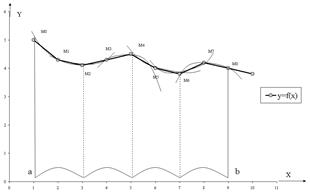
Рис.2.8 Геометричне тлумачення формули Симпсона
Візьмемо 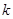 -й подвоєний відрізок, функцію -й подвоєний відрізок, функцію 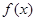 проінтегруємо на цьому відрізку, використовуючи квадратурну формулу (2.3.1) з похибкою (2.3.5) проінтегруємо на цьому відрізку, використовуючи квадратурну формулу (2.3.1) з похибкою (2.3.5)
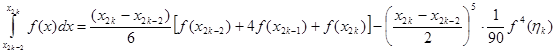
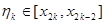 .
.
Просумувавши інтеграли за всіма подвоєними відрізками, добудемо узагальнену формулу Сімпсона
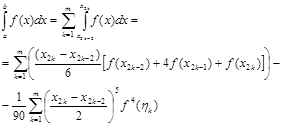 
Якщо прийняти умову, що відстань між будь-якими двома сусідніми вузлами однакові і дорівнює 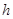 , то останню формулу можна переписати в більш простому вигляді , то останню формулу можна переписати в більш простому вигляді
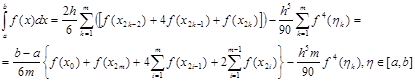
Тепер запишемо окремо узагальнену формулу Сімпсона та її похибку
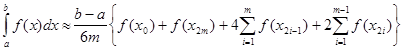 (2.3.7) (2.3.7)
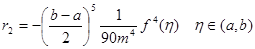 (2.3.8) (2.3.8)
Геометричне зображення формули (2.3.7) показане на рисунку (2.8).
Наближене значення інтеграла (права частина наближеної рівності (2.3.7) - це площа криволінійної трапеції, яка зверху обмежена кусками парабол 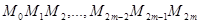 (крива показана пунктиром). (крива показана пунктиром).
На кожному подвоєному відрізку графік функції 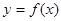 наближається своєю параболою. наближається своєю параболою.
З формули (2.3.7) видно, що з ростом 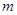 похибка дуже швидко зменшується. похибка дуже швидко зменшується.
Застосовуючи ці три метода наведемо приклад:
Обчислимо наближене значення інтеграла
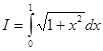 , ,
використовуючи квадратурні формули прямокутників, трапеції та Сімпсона. Для цього підготуємо таблицю значень підінтегральної функції 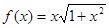 у точках відрізка у точках відрізка 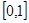
| Значення підінтегральної функції у вузлах |
| i |
xi
|
f (xi
) |
| 0 |
0 |
0,00000000 |
| 1 |
0,1 |
0,10049875 |
| 2 |
0,2 |
0, 20396078 |
| 3 |
0,3 |
0,31320918 |
| 4 |
0,4 |
0,43081316 |
| 5 |
0,5 |
0,55901695 |
| 6 |
0,6 |
0,69971418 |
| 7 |
0,7 |
0,85445885 |
| 8 |
0,8 |
1,0244998 |
| 9 |
0,9 |
1,2108262 |
| 10 |
1 |
1,4142135 |
Квадратурні формули прямокутників (лівих, правих, центральних) дать такі результати:
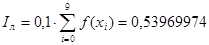 , , 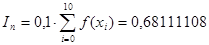
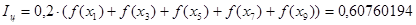
У цьому прикладі інтеграл такий, що його точне значення можна обчислити, воно дорівнює (з точністю до сьомого розряду після коми)
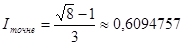
Зауважимо, що хоча формула центральних прямокутників у цьому прикладі використана з вдвічі більшим кроком, ніж формули лівих та правих прямокутників, але результат вийшов ближчим до точного, ніж у двох інших методів.
За квадратурними формулами трапецій та Симпсона маємо такі результати:
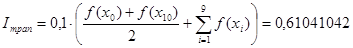
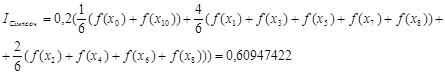
Отже після обчислень за різними квадратурними формулами маємо такі наближені значення інтеграла:
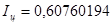 ; ; 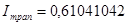 ; ; 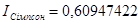
З використаних формул більш точною є формула Симпсона, оскільки її алгебраїчний степінь точності на дві одиниці більший ніж у формули трапеції. Тому, користуючись апостеріорним методом оцінки похибки, в результаті, добутому за формулою Симпсона можна вважати три розряди після коми правильними, а четвертий розряд округленим тобто
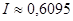
Але, якщо порівняти з точним значенням інтеграла, то видно, що насправді результат, добутий за формулою Симпсона, має п’ять правильних розрядів після коми, шостий розряд округлений.
Задача графічного інтегрування полягає в наступному: за графіком неперервної функції 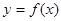 потрібно побудувати графік її первісної функції. потрібно побудувати графік її первісної функції.
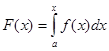 (3.1) (3.1)
Іншими словами, потрібно побудувати таку криву 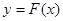 , ордината в кожній точці якої чисельно дорівнює площі криволінійної трапеції з основою , ордината в кожній точці якої чисельно дорівнює площі криволінійної трапеції з основою 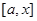 , обмеженою даною кривою , обмеженою даною кривою 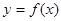 . .
Для наближеної побудови графіка первісної функції 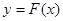 розбиваємо площу відповідної криволінійної трапеції, обмеженої кривій розбиваємо площу відповідної криволінійної трапеції, обмеженої кривій 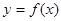 , на вузькі вертикальні смужки за допомогою ординат, проведених у точках , на вузькі вертикальні смужки за допомогою ординат, проведених у точках 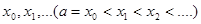 (рис.3.1) [2]. (рис.3.1) [2].
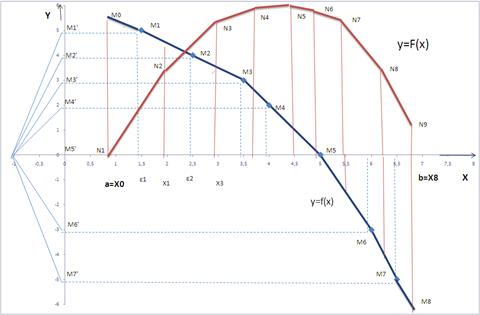
Рис.3.1 Графічне інтегрування функції f (x) з отриманням первісної функції F (x) [2]
Кожну з таких смужок заміняємо, використовуючи теорему про середнє, рівновеликим (по можливості) прямокутником з тією ж основою і висотою, рівною 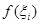 , , 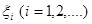 , , де деяка проміжна точка де деяка проміжна точка  -го по порядку відрізка -го по порядку відрізка 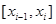 , тобто думаємо: , тобто думаємо:
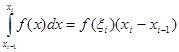 (3.2) (3.2)
Де
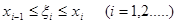 (3.3) (3.3)
Значення первісної функції
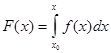 (3.4) (3.4)
у точках 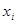 можна підрахувати методом нагромадження: можна підрахувати методом нагромадження:
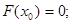
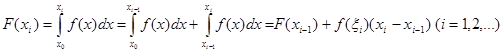 (3.5) (3.5)
Нехай 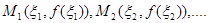 - відповідні точки кривої - відповідні точки кривої 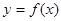 . Проектуючи їх на вісь . Проектуючи їх на вісь 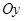 одержимо точки одержимо точки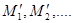 (рис.3.1). (рис.3.1).
Виберемо тепер полюс 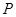 із відстанню із відстанню 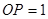 й проведемо промені й проведемо промені 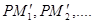 . Розраховуєму первісну функцію - лінію . Розраховуєму первісну функцію - лінію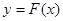 приблизно можна замінити ламаною приблизно можна замінити ламаною 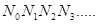 з вершинами з вершинами 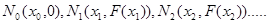 . Послідовні ланки цієї ламаної будуть паралельні відповідним променям, а саме: . Послідовні ланки цієї ламаної будуть паралельні відповідним променям, а саме: 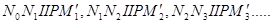 . Справді, кутовий коефіцієнт ланки . Справді, кутовий коефіцієнт ланки 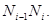 на підставі формули (1) дорівнює на підставі формули (1) дорівнює
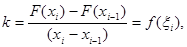 (3.6) (3.6)
У силу ж побудови кутовий коефіцієнт променів 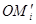 якщо якщо
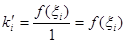 (3.7) (3.7)
Отже
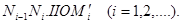 (3.8) (3.8)
Таким чином, технічно побудова графіка функції 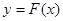 може бути здійснена так: може бути здійснена так:
із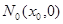 точки проводимо пряму точки проводимо пряму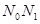 паралельну променю паралельну променю 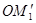 , до перетину в точці , до перетину в точці 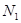 з вертикаллю з вертикаллю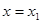 ; ;
із точки 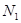 проводимо пряму проводимо пряму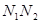 паралельну променю паралельну променю 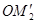 , до перетину в точці , до перетину в точці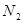 з вертикаллю з вертикаллю 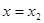 й так далі. й так далі.
Слід зазначити, що при застосуванні даного методу графічного інтегрування точки 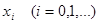 не обов'язково брати рівновіддаленими. Для збільшення точності побудови рекомендуються характерні точки графіка інтегрувальної функції (нулі, точки екстремуму, точки перегину) обов'язково включати до складу точок не обов'язково брати рівновіддаленими. Для збільшення точності побудови рекомендуються характерні точки графіка інтегрувальної функції (нулі, точки екстремуму, точки перегину) обов'язково включати до складу точок 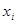 . .
Висновок: Графічне інтегрування володіє, взагалі говорячи, малою точністю. Тому цей прийом корисно використовувати тоді, коли потрібно мати загальне подання про інтеграл функції або коли підінтегральна функція задана графічно і її аналітичне вираження нам невідомо.
1. Бойко Л.Т. Основи чисельних методів: навч. посібник. - Д.: Вид-во ДНУ, 2009. - 244 с.
2. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Изд-во „Наука” - „Физматлит", 1979. - 664 с.
3. Канторович А. В., Крылов В.И. Приближенные методы высшего анализа. - М.: Изд. Физико-математической литературы, 1962. - 708 с.
4. Крылов В.И. Вычислительные методы: учебное пособие / В.И. Крылов, В.В. Бобков, П.И. Монастырный. - М.: „Наука”, 1976. - Т.1. - 304 с.
5. Крылов В.И. Вычислительные методы: учебное пособие / В.И. Крылов, В.В. Бобков, П.И. Монастырный. - М.: „Наука”, 1977. - Т.2. - 399 с.
6. Марчук Г.И. Методы вычислительной математики. Схемы, таблицы. - М.: " Наука", 1977. - 456 с.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. - М.: „Наука”, 1970. - Т.2. - 800 с.
|