План

Введение

I. Теоретические основы исследования применения общедидактических принципов в организации занятий по развитию математических представлений у детей в ДОО

1.1 Принципы обучения как категория дидактики

1.2 Современные проблемы дидактических принципов обучения

1.3 Реализация общедидактических принципов в организации занятий в ДОО

II. Экспериментальная работа по применению общедидактических принципов в организации занятий по развитию математических представлений в ДОО

2.1 Констатирующий этап эксперимента

2.2 Формирующий этап эксперимента

2.3 Контрольный этап эксперимента

Выводы

Литература

Приложения

Введение

Ребенок очень много может усвоить в первые годы жизни. Период дошкольного детства относительно всей жизни человека недолог, но очень насыщен познанием. Велик поток информации, который обрушивает на маленького человека окружающая жизнь.

Источником познания дошкольника является чувственный опыт. Спонтанно накопленный чувственный и интеллектуальный опыт может быть объемным, но не упорядоченным, неорганизованным. Направить его в нужное русло призван педагог, который не только знает, чему учить ребенка, но и как учить, чтобы обучение было развивающим.

Обучению дошкольников основам математики отводиться важное место. Это вызвано целым рядом причин: обилием информации, получаемой ребенком, повышенное внимание к компьютеризации, желанием сделать процесс обучения более интенсивным. [1]

Программа по математике в детском саду направлена на развитие и формирование математических представлений и способностей, логического мышления, умственной активности, смекалки, то есть умения делать простейшие суждений, пользоваться грамматически правильными оборотами речи.

На занятиях по математике воспитатель осуществляет не только образовательные задачи, но и решает воспитательные. Педагог знакомит дошкольников с правилами поведения, воспитывает у них старательность, организованность, привычку к точности, сдержанн6ость, настойчивость, целеустремленность, активное отношение к собственной деятельности. [3]

Когда говорят о процессе организации занятий как сложной системе, включающей в себя учебную деятельность воспитателя и учебную деятельность воспитанника, имеют в виду организованное обучение.

Но обучение не может быть организованным, если оно не опирается на объективно существующие или предполагаемые закономерности.

Сформулированные как нормативные положения, которыми следует руководствоваться, эти закономерности, реальные или предполагаемые, становятся принципами обучения. [6]

Проблема исследования применения дидактических принципов в организации занятий с детьми дошкольного возраста носит актуальный характер на современном этапе. Об этом свидетельствует частое изучение поднятых вопросов; данная тема изучается на стыке сразу нескольких взаимосвязанных дисциплин; требуется учет современных условий при исследовании проблематики обозначенной темы; высокая значимость и недостаточная практическая разработанность проблемы.

Актуальность изучения применения общедидактических принципов в организации занятий по развитию элементарных математических представлений обусловлена, с одной стороны, большим интересом к данному вопросу в современной педагогике, с другой стороны, его недостаточной разработанностью.

Объектом данного исследования является анализ условий применения общедидактических принципов в организации занятий по развитию математических представлений у детей в детском саду.

Предметом исследования является рассмотрение отдельных вопросов, сформулированных в качестве задач данного исследования.

Целью исследования является теоретическое и практическое изучение темы с точки зрения современных исследований по сходной проблематике.

В рамках достижения поставленной цели поставлены следующие задачи:

1. Изучить теоретические аспекты проблемы "Применение общедидактических принципов в организации занятий по РЭМП у детей в детском саду";

2. Исследовать условия и значение применения дидактических принципов в организации занятий по развитию математических представлений в детском саду;

3. Выявить на практике роль применения общедидактических принципов в повышении уровня математического развития дошкольников в современных образовательных учреждениях.

I. Теоретические основы исследования применения общедидактических принципов в организации занятий по развитию математических представлений у детей в ДОО

1.1 Принципы обучения как категория дидактики

Процесс обучения, являясь составной частью целостного педагогического процесса, в современном образовании, в том числе и дошкольном, направлен на формирование всесторонне и гармонически развитой личности.

Обобщенный опыт организации занятий по усвоению основ науки показывает, что для обеспечения единого подхода к воспитанникам, к выбору средств и методов учебной работы воспитатель должен придерживаться положений, носящих универсальный характер. [1]

В связи с этим в дидактике разработаны принципы, которые рассматриваются как важнейшие требования к организации процесса обучения, его содержанию, формам и методам. Эти единые требования получили название дидактических принципов или принципов обучения. Организация процесса обучения в соответствии с дидактическими принципами позволяет построить его на научной основе.

Вместе с тем следует иметь в виду, что дидактические принципы, выражая определенные закономерности обучения и передовой опыт учебно-воспитательной деятельности дошкольного обучения, не являются раз и навсегда установленными. Они постоянно углубляются и видоизменяются в соответствии с теми задачами, которые ставит перед образованием общество. [2]

Таким образом, общедидактические принципы – это основные направляющие положения, возникающие в результате анализа научно – педагогических закономерностей и практического педагогического опыта. Они являются главным ориентиром в педагогической работе воспитателя.

Основные дидактические принципы, которыми и на современном этапе организации занятий руководствуются педагоги, в том числе и дошкольного образования, провозгласил К.Д. Ушинский. По его мнению, обучение может выполнить образовательные и воспитательные задачи лишь в том случае, если оно будет соблюдать три основные условия: связь с жизнью, соответствие с природой ребенка и особенностями его психофизического развития, и обучения на родном языке. [15]

Доступность обучения (природосообразность) – содержание обучения должно быть адаптировано с учетом умственных и физических возможностей детей, достигнутого ими уровня знаний и умений, развития. Вместе с тем изучаемый материал должен требовать от детей определенных усилий для его усвоения.

Принцип научности обучения – научный уровень знаний должен сочетаться с доступностью и яркостью изложения, служить задачам нравственного и эстетического воспитания; должен содержать материал для наблюдений. [6]

К.Д. Ушинский утвердил в русской дидактике принцип воспитывающего обучения (единства обучения и воспитания) – если развитие, формирование и воспитание личности осуществляется в единстве своем через обучение, то само обучение неизбежно должно быть развивающим и воспитывающим. Наука должна действовать не только на ум, но и на душу, чувство.

Систематичность и последовательность в обучении – знания и умения детей должны представлять собой определенную систему, а их формирование – осуществляться в такой последовательности, чтобы изучаемый элемент был логически связан с предыдущими элементами.

Успеха в обучении можно достигнуть при сочетании чувственной и абстрактной деятельности: ощущения должны превращаться в понятия, из понятий - составляться мысль, облеченная в слово. Обучение должно включать непосредственное восприятие детьми конкретных образов изучаемых объектов, процессов и действий.

Про наглядное обучение К.Д. Ушинский писал: «Что такое наглядное обучение? Да это такое ученье, которое строится не на отвлеченных представлениях и словах, а на конкретных образах, непосредственно воспринятых ребенком: будут ли эти образы восприняты при самом ученье, под руководством наставника, или прежде, самостоятельным наблюдением ребенка... Детская природа ясно требует наглядности». [16]

Сознательность, активность и самостоятельность учащихся в обучении – необходимо активное овладение детьми знаниями и умениями на основе их осмысления, творческой переработки и применения в процессе самостоятельной работы, сотрудничества педагога и воспитанников в осознанном достижении целей обучения.

Известные советские дидакты М.А. Данилов, И.Я. Лернер, М.Н. Скаткин в своих исследованиях показали, что принципы обучения, являясь категориями дидактики, характеризуют способы использования законов и закономерностей обучения в соответствии с целями воспитания и образования.

Дидактические принципы – это принципы деятельности, представляющие собой наиболее общее нормативное знание о том, как надо строить, осуществлять и совершенствовать обучение и воспитание. Закономерности этой деятельности являются теоретической основой для выработки норм образовательно-воспитательной работы педагога. Однако сами по себе они не содержат конкретных указаний для такой деятельности. Эти указания дают принципы.

Таким образом, принципы обучения взаимообусловлены его закономерностями.

Однако, кроме законов и закономерностей обучения в становлении принципов, учитываются и другие факторы, а именно:

1) цели, которые ставит общество перед обучением и воспитанием;

2) конкретные условия, в которых осуществляется учебный процесс;

3) психологические характеристики процесса учения;

4) существующие способы конструирования учебных и воспитательных ситуаций.

Здесь следует заметить, что если речь идет не о дидактическом, а о методическом принципе, то в этом случае должна учитываться специфика конкретного учебного раздела и его функции в общем образовании. [7]

1.2 Современные проблемы дидактических принципов обучения

Современная педагогика и дидактика, опираясь на основные общедидактические принципы, пока не могут предложить окончательно сформированную систему принципов обучения. Совершенно очевидно, что одной из серьезных причин этого является отсутствие удовлетворительного единого основания для классификации принципов обучения. Отдельные принципы традиционно отнесены то к содержанию, то к методам, то к организации обучения. Некоторые из них относятся не столько к учебной, сколько к воспитательной стороне педагогического процесса. [4]

Следовательно, необходимо договориться о едином основании для классификации принципов обучения, охватывающем все стороны единого образовательно – воспитательного процесса, а также все его компоненты. Вместо перечня принципов следовало бы разработать действительно систему принципов обучения в полном значении этого слова. Унифицировав формулировки отдельных принципов, надо бы дать научное обоснование каждому из них, а также всей системе в целом и более точно определить взаимодействие принципов с другими категориями педагогики (цель, содержание и формы, методы и организация учебного процесса).

В этом плане есть работы – исследования Л.В. Занкова и его лаборатории. Им разработаны и сформулированы 5 совершенно новых принципов дошкольного и начального обучения. [11]

Своеобразно подошел к классификации принципов обучения В.В. Давыдов. Он критиковал как закосневшие и тривиальные традиционно устоявшиеся принципы преемственности, доступности, сознательности, наглядности и научности и предложил новую трактовку принципов.

1. Преемственность — это связь качественно различного между разными стадиями обучения, начиная с детского сада и младших классов, заканчивая старшими. Например, от опыта житейских знаний дошкольника — к сформированности учебной деятельности в младших классах.

2. Принцип развивающего обучения — это всесторонне раскрытый принцип, “при котором можно закономерно управлять темпами и содержанием развития посредством организации обучающих воздействий”.

3. Принцип деятельности, по В.В. Давыдову, противостоит традиционно толкуемому принципу сознательности. Эти значит, что дошкольники, а в последствие школьники, получают знания не в готовом виде, а сами “выясняют условия их происхождения” посредством “специфических действий преобразования предметов”.

4. Принцип предметности противостоит принципу наглядности. Он означает точное указание “тех специфических действий с предметами, чтобы, с одной стороны, выявить содержание будущего понятия, с другой — изобразить это первичное содержание в виде знаковых моделей”. [12]

Заканчивая разговор об общедидактических и психолого - дидактических принципах обучения, можно сделать некоторые выводы:

1. Дидактические принципы имеют длинный исторический путь развития. Большинство из них найдены опытным путем и существуют традиционно. В процессе развития педагогической теории эти принципы приобретают научное обоснование, имеют нормативный характер и способствуют эффективному построению учебного процесса.

2. Развивающейся в последнее время дидактике в рамках традиционной номенклатуры принципам обучения стало тесно. Практика педагогов-новаторов подсказала некоторые новые принципы. Они дополняют, уточняют и улучшают традиционные. Например, принцип межпредметных связей, бесконфликтности, обратной связи, успеха (В.Ф. Шаталов); художественности (Б.М. Неменский), взаимного обогащения учащихся знаниями (Х.Й. Лийметс, М.Н. Скаткин).

3. Новые концепции обучения вызвали к жизни и новые принципы. Идея развивающего обучения по концепции Л.В. Занкова выдвинула систему из 5 принципов. Та же идея в соответствии с концепцией Д.Б. Эльконина—

В.В. Давыдова потребовала коренного пересмотра традиционных. Новые концепции обучения, например, личностно ориентированного, наверняка подвергнут ревизии традиционные принципы и подскажут новые. [10]

1.3 Реализация общедидактических принципов в организации занятий в ДОО

В дошкольном возрасте закладываются основы знаний, необходимых ребенку в школе. Математика представляет собой сложную науку, которая может вызвать определенные трудности во время школьного обучения. К тому же далеко не все дети имеют склонности и обладают математическим складом ума, поэтому такое важное значение имеет оптимальная организация занятий при математической подготовке детей к школе.

И родители, и педагоги знают, что математика – это мощный фактор интеллектуального развития ребенка, формирования его познавательных и творческих способностей. Самое главное – это привить ребенку интерес к познанию. Для этого занятия должны строиться с учетом всех общедидактических принципов, проходить в увлекательной игровой форме.

Постепенно у детей пробуждается интерес и к самому предмету обучения.

Обучение математике, как и любому учебному предмету, может стать эффективным средством формирования личности, достичь непосредственной цели – прочного и сознательного усвоения ее содержания – лишь в случае, если в основу обучения будут положены определенные положения, вытекающие из основных закономерностей дидактики, подтвержденные опытом обучения. [13]

Система таких положений, специально ориентированная на особенности математики как учебного предмета, и составляет основное содержание общедидактических принципов, применяемых в организации занятий по РЭМП. Наиболее важные принципы, характеризующие подход к обучению основам математики в детском саду, – принцип наглядности, принцип воспитывающего обучения, принцип научности, принцип сознательности и активности обучения, принцип систематичности и последовательности и др. Владение этими принципами необходимо педагогу для того, чтобы правильно организовать свой труд, грамотно, квалифицированно анализировать различные учебные пособия и методические разработки, которыми ему придется пользоваться в своей работе. [8]

А.А. Столяр предлагает систему общедидактических принципов дополнить двумя принципами, характерными для обучения математике:

1) курс математики должен отражать фундаментальные идеи и логику современной математики (в соответствии с уровнем мыслительной деятельности дошкольников на разных возрастных этапах);

2) процесс обучения математике должен строиться подобно процессу исследования в математике, то есть, он должен имитировать процесс творческого поиска в математике (в определенной мере, в какой это допускает уровень мыслительной деятельности детей дошкольного возраста).

Первый принцип относится к построению содержания обучения математике и в определенной степени конкретизирует дидактический принцип научности.

Второй принцип относится к построению процесса обучения и конкретизирует дидактический принцип развивающего обучения. [14]

В методической литературе по математическому развитию общепризнанной является следующая система дидактических принципов:

1. Принцип воспитания в развитии математических представлений.

2. Принцип научности в обучении математике.

3. Принцип сознательности, активности и самостоятельности в развитии математических представлений.

4. Принцип систематичности и последовательности в развитии математических представлений.

5. Принцип доступности в развитии математических представлений.

6. Принцип наглядности в развитии математических представлений.

7. Принцип индивидуального подхода к учащимся в развитии математических представлений.

Принцип воспитания

Общей целью воспитания в детском саду является подготовка к всестороннему развитию личности, способной построить и защитить общество. Всестороннее развитие личности предполагает умственное и нравственное развитие, богатую духовную жизнь, физическое и эстетическое развитие. Реализация общей цели воспитания требует поэтому решения более частных задач, которые рассматриваются в качестве составных частей или сторон воспитания: трудовое, нравственное, умственное, эстетическое и физическое воспитание. Выделение составных частей воспитания опирается на объективные требования общества в развитии определенных свойств (качеств) личности. [5]

Но воспитание в процессе обучения вообще и математике в частности как принцип обучения имеет и свою содержательную направленность, которая определяется формированием мировоззрения и морали. Чтобы каждый ребенок мог действовать в соответствии с принципами мировоззрения и морали, он должен сформировать у себя такие черты характера, как трудолюбие, сила воли, скромность, честность по отношению к самому себе и другим людям.

Мировоззрение, базирующееся на научном знании и практическом жизненном опыте, связывает в единое целое эти свойства личности. Отсюда вытекают возможность и необходимость передачи всем людям знаний о закономерностях развития природы, общества и человеческого мышления, чтобы они могли сознательно осуществлять практическую деятельность. [9]

Следовательно, в формировании убеждений возрастает роль процесса усвоения знаний. В связи с этим в развитии математических представлений (как и каждого раздела образовательной программы) необходимо повышать активность детей и возбуждать у них интерес к вопросам, имеющим мировоззренческое значение. Важную роль в этом приобретает освещение в преподавании математики новых идей современной науки.

При планировании содержания, средств, методов и форм обучения педагог призван обеспечить решение всего комплекса образовательных, воспитательных и развивающих задач. [5]

Принцип научности

Требование научности содержания образования было выдвинуто в советской педагогической литературе еще в работах Н. К. Крупской.

Статус дидактического принципа требование научности в обучении приобрело с 1950г., когда оно было сформулировано и обосновано М. Н. Скаткиным. В дальнейшем Л.Я. Зорина показала, что под научностью содержания образования следует понимать такую его качественную характеристику, которая удовлетворяет трем признакам:

а) соответствие содержания образования уровню современной науки;

б) создание верных представлений об общих методах научного познания;

в) показ важнейших закономерностей процесса познания. [12]

Эти условия взаимосвязаны между собой, ибо реализация каждого из последующих обусловлена выполнением предыдущих; каждое предыдущее условие является необходимой базой для реализации последующего.

В организации занятий по развитию математических представлений дошкольников у педагогов имеется много возможностей показать закономерности процесса познания. Именно поэтому в процессе обучения основам математике шире должны внедряться проблемное обучение и разнообразные исследовательские приемы.

В процессе реализации принципа научности воспитатель должен соблюдать также принцип доступности, чтобы содержание, формы и методы обучения учитывали реальные возможности воспитанников. При этом необходимо учитывать и то, что принцип доступности предполагает обучение на достаточно высоком уровне трудности. Однако это можно достигнуть лишь при наилучшем сочетании индивидуальных и коллективных форм познавательной деятельности дошкольников в обучении.

Принцип систематичности и последовательности

Нельзя овладеть наукой, не изучая ее в определенной системе. В такой же мере нельзя успешно развивать познавательные и творческие способности дошкольников без строго продуманной системы их обучения и воспитания.

Систематичность в развитии математических представлений предполагает соблюдение определенной последовательности в изучении учебного материала и постепенное овладение основными понятиями дошкольного курса математики.

Последовательность в обучении математике означает, что обучение осуществляется в соответствии с правилами обучения: а) от простого к сложному; б) от легкого к трудному; в) от известного к неизвестному;

г) от представлений к понятиям; д) от знания к умению, от него к навыку. [7]

Принцип доступности

Принцип доступности в обучении вытекает из требований учета возрастных и индивидуальных особенностей детей дошкольного возраста. Он лежит в основе составления учебных планов и программ.

Принцип доступности требует, чтобы объем и содержание предлагаемого воспитателем материала были по силам воспитанникам, соответствовали уровню их умственного развития и имеющемуся у них запасу знаний, умений и навыков.

Реализация принципа доступности в развитии математических представлений предполагает выполнение следующих дидактических условий: а) следовать в обучении от простого к сложному; б) от легкого к трудному; в) от известного к неизвестному. [16]

Отсюда следует, что строгое соблюдение в обучении принципа систематичности и последовательности предопределяет успешную реализацию принципа доступности.

Принцип доступности в дошкольном образовании привлекает к себе особое внимание также в связи с проблемой индивидуального подхода к воспитанникам в условиях массового обучения в детском саду.

Принцип сознательности, активности и самостоятельности

Данный принцип заключается в целенаправленном активном восприятии изучаемых явлений, их осмыслении, творческой переработке и применении. Он вытекает из целей и задач дошкольного образования, а также из особенностей процесса обучения, требующего осмысленного и творческого подхода к изучаемому материалу.

Реализация принципа сознательности, активности и самостоятельности в обучении предполагает выполнение следующих условий:

а) соответствие познавательной деятельности детей закономерностям процесса учения;

б) познавательная активность воспитанников в процессе занятия;

в) осознание дошкольниками процесса приобретения знаний, умений и навыков;

г) овладение детьми дошкольного возраста методами умственной работы в процессе познания нового.

Сознательность понимается в дидактике как овладение учащимися данными науки, учебным материалом, осмысление его, умение пользоваться полученными знаниями на практике в новых условиях, превращение знаний в убеждения, в руководство к действию. [5]

Принцип наглядности

Теоретическое обоснование принципу наглядности впервые было дано чешским педагогом Я.А. Коменским, который выдвинул требование учить людей познавать самые вещи, а не только чужие свидетельства о них.

Принцип наглядности вытекает из сущности процесса восприятия, осмысления и обобщения детьми изучаемого материала.

Говоря о значении принципа наглядности и о его роли в процессе учебного познания, дидактика утверждает, что наглядность является исходным моментом обучения основам математических знаний главным образом в дошкольном возрасте и в младших классах.

Наглядность применяется и как средство познания нового, и для иллюстрации мысли, и для развития наблюдательности, и для лучшего запоминания материала. Средства наглядности используются на всех этапах процесса обучения: при объяснении нового материала воспитателем, при закреплении знаний, формировании умений и навыков, при выполнении самостоятельных заданий, при контроле усвоения учебного материала.

Принцип наглядности, по выражению Я.А. Коменского, является "золотым правилом дидактики". Он требует сочетания наглядности и мысленных действий, наглядности и слова. [1]

Принцип индивидуального подхода

Повышение эффективности обучения непосредственно связано с тем, насколько полно учитываются особенности каждого ребенка. Важной индивидуальной особенностью детей, в том числе и дошкольного возраста, является их способность к усвоению знаний.

Как показали многочисленные психолого-дидактические исследования, если уровнять многие факторы, влияющие на уровень усвоения новых знаний, а именно: обеспечить одинаковый исходный минимум знаний у всех воспитанников, положительное отношение их к занятию, желание как можно лучше усвоить материал, тщательно разработать методику введения нового материала, то, несмотря на равенство этих условий, новые знания будут усвоены по разному.

Следует заметить, что изучение разных сторон мыслительной деятельности позволило психологам сделать предположение о том, что не всякое усвоение знаний означает сдвиг в умственном развитии учащегося. Этот сдвиг происходит тогда, когда обучение обеспечивает овладение не только содержанием знаний, но и методами, способами их приобретения, благодаря чему дети могут самостоятельно приобретать новые знания. [11]

Отмеченные выше явления, имеющие место в развитии математических представлений дошкольников, показали невозможность создать в обучении систему, равно оптимальную для каждого воспитанника. Это обстоятельство привело к необходимости реализации в обучении принципа индивидуального подхода к каждому ребенку.

Таким образом, с учетом всего вышеперечисленного, уверенно можно говорить о том, что прочное и сознательное усвоение элементарных математических представлений детьми дошкольного возраста возможно лишь в случае применения в организации занятий по развитию математических представлений общедидактических принципов. [13]

II . Экспериментальная работа по применению общедидактических принципов в организации занятий по развитию математических представлений в ДОО

2.1 Констатирующий этап эксперимента

Для проведения экспериментальной работы мною была выбрана средняя группа № 4 МДОУ «Бендерский Детский сад № 25», из которой отобраны 16 детей и сформированы две подгруппы – экспериментальная и контрольная – по 8 человек с приблизительно одинаковым уровнем развития математических представлений.

Вначале была проведена диагностика уровня развития детей по трем разделам программы математического развития:

- Количество;

- Величина;

- Счет, число.

За основу диагностики были взяты прежде всего результаты наблюдений за ребенком на занятиях и в повседневной жизни, а также диагностические методики, предложенные А.В. Белошистой:

- Сосчитай, сколько здесь кругов (5 кругов расположены в беспорядке).

- Сосчитай, сколько здесь квадратов (4 квадрата расположены в ряд).

- Где фигур больше: там, где 5, или там, где 4?

- Что можно сосчитать в группе? Сосчитай.

- А дома что у тебя можно сосчитать? Вспомни, сосчитай и скажи сколько?

- Возьми круги (4) и квадраты (5). Как узнать, поровну ли их? Или квадратов больше, чем кругов? Какое число больше: 4 или5? Какое число меньше: 5 или 4?

- Ребёнку предлагается посчитать (5) маленьких матрёшек и (5) больших мишек. Каких предметов больше: маленьких матрёшек или больших мишек; Как проверить?

- Ребёнку предлагается посчитать квадраты (4), расположенные по кругу и в линию. Где меньше квадратов: там, где они расположены в линию или по кругу? Как проверить?

- Ребёнку предлагается посчитать грибы (5), расположенные близко и далеко друг к другу. Где грибов больше: там, где они стоят близко или далеко друг от друга?

К высокому уровню развития отнесены те дети, которые владеют навыками сосчитывания предметов (до 8-10), обнаруживают зависимости и отношения между числами. Владеют навыками наложения и приложения предметов с целью доказательства их равенства и неравенства. Устанавливают независимость количества предметов от их расположения в пространстве путём сопоставления, сосчитывания предметов (на одном и том же количестве предметов). Осмысленно отвечают на вопросы, поясняют способ сопоставления, обнаружения соответствия.

Дети со средним уровнем развития в достаточной степени владеют навыками сосчитывания предметов (до 4-7), пользуясь при этом приёмами наложения и приложения с целью доказательства равенства и неравенства. С помощью взрослого устанавливают независимость количества предметов от их расположения в пространстве. Но затрудняются в высказываниях и пояснениях.

Низкий уровень развития диагностирован у тех детей, которые допускают ошибки при сосчитывании предметов (до 3-5), не обнаруживают зависимости и отношений между числами. Плохо владеют приемами наложения и приложения; даже с помощью взрослого с трудом устанавливают независимость количества предметов от их расположения в пространстве.

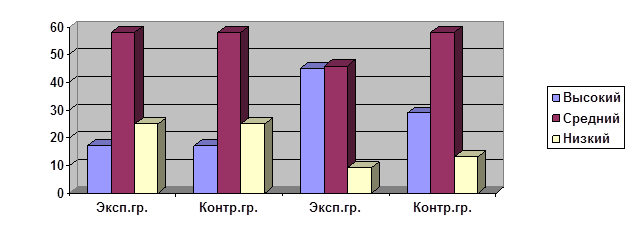
В результате сравнительного анализа диагностических данных видно, что перед началом эксперимента в обеих группах высокий уровень развития составил 17%, средний – 58%, а низкий – 25%.(Приложение № 1, 2)

Наблюдение показало, что дети лучше всего освоили сравнение предметов по величине и групп предметов по количеству. Большинство успешно справляется со сравнением множеств, с сопоставлением элементов одного множества с элементами другого, различают равенство и неравенство групп предметов, составляющих множество.

Наиболее высокий уровень усвоения материала связан у дошкольников с развитием первоначальных представлений о величине предметов контрастных и одинаковых размеров по длине, ширине, высоте, толщине, объему. Такжегруппировка предметов по признакам вырабатывает у детей умение сравнивать, осуществлять логические операции классификации.

В процессе разнообразных практических действий с совокупностями дети хорошо усвоили и большинство умеет использовать в речи простые слова и выражения, обозначающие уровень количественных представлений: много, один, по одному, ни одного, совсем нет, мало, такой же, одинаковый, столько же, поровну; столько, сколько; больше, чем; меньше, чем; каждый из, все, всех.

Трудности у большинства испытуемых вызвали навыки устного счета и знакомство с числами. Слабо сформировано понятие о возникновении каждого нового числа путем добавления единицы.

Низкий уровень развития дети средней группы показали также при освоении таких приемов, как сравнение двух чисел, сопоставление, установление равенства и неравенства их. Почти все дошкольники испытывают трудности в умении отличать порядковый счет от количественного, хотя с порядковым счетом в пределах 1 – 5 справилось большинство детей.

Таким образом, на констатирующем этапе эксперимента сформированы две группы детей среднего дошкольного возраста – экспериментальная и контрольная – с приблизительно равным уровнем развития элементарных математических представлений; заполнены диагностические карты на начало эксперимента; выявлены наиболее слабые показатели уровня математического развития в целом по разделу и по отдельным его частям.

2.2 Формирующий этап эксперимента

При проведении эксперимента в процессе наблюдения за деятельностью воспитателей на занятиях по развитию элементарных математических представлений у дошкольников средней группы мною отмечено, что при подготовке и проведении занятия педагоги реализуют основные общедидактические принципы, но недостаточно полно.

При составлении конспекта и подборе материала для реализации образовательных задач в полной мере реализуется принцип научности, учитываются новейшие достижения и технологии. Но именно на занятиях по математическому развитию дошкольников слабо учитывается принцип воспитывающего обучения.

В связи с этим для организации и проведения занятий в экспериментальной группе мною составлялись конспекты, рассчитанные не только на развитие математических представлений у детей, но и направленные на воспитание таких качеств, как самостоятельность, взаимопомощь и взаимовыручка (Приложение № 3, 4, 5).

При проведении математического КВН велось постоянное наблюдение за тем, чтобы дошкольники проявляли дружелюбное и уважительное отношение не только к членам своей команды, но и к соперникам; ощущали в них партнеров по овладению знаниями, а не врагов. Также обращалось внимание на эмоционально положительный настрой детей, поддержку у них творческой любознательности и стремления к достижению конечного результата.

Математические занятия – развлечения, проводимые с дошкольниками средней группы, кроме закрепления полученных на занятиях по развитию математических представлений знаний преследовали цель расширить представления детей о дружбе, причинах возникновения конфликтов и способах их предотвращения, воспитывать у детей доброжелательное отношение к животным и игровым персонажам. А также познакомить дошкольников с элементарными представлениями о морали.

Кроме того, все конспекты математических занятий для экспериментальной группы предусматривали развитие внимания, сообразительности, смекалки, а также формирование волевых качеств и поддержку интереса к интеллектуальной деятельности в целом.

Воспитателями группы при планировании учитывается принцип последовательности и систематичности, соблюдается определенная последовательность в изложении учебного материала и постепенное овладение основными математическими представлениями. Но при этом не в полной мере осуществляется взаимосвязь между разными разделами программы, отсутствует система между осваиваемым во время занятия и в свободной деятельности. Поэтому во время проведения экспериментальной деятельности была расширена сфера применения принципа последовательности и систематичности путем установления теснейшей связи при развитии математических представлений между разными видами деятельности детей – дошкольников. В результате этого воспитанники осознают приобретенные ими знания как элементы целостной, единой системы, и получают возможность практического использования этих знаний в условиях повседневности.

Принципы доступности и индивидуального подхода в работе с дошкольниками привлекают к себе особое внимание в связи с проблемой массовости в обучении. Большинство предусмотренного программой материала рассчитано на передачу его детям в фронтальных и, реже, групповых формах занятий. При этом учитываются возрастные особенности детей, но значительно затруднен учет индивидуальных различий. Сущность принципа индивидуального подхода, по существу, состоит в адаптации (приспособлении) материала либо к содержанию и уровню знаний, умений и навыков каждого воспитанника, либо также к характерным для него особенностям процесса усвоения, либо даже к некоторым устойчивым особенностям его личности.

Поэтому для более эффективной реализации данного принципа при развитии математических представлений на занятиях с экспериментальной группой чаще использовались индивидуальные самостоятельные работы, элементы дидактических игр. Также при составлении конспектов математических занятий, занятий – игр и занятий – развлечений предусматривались задания разной направленности и разного уровня сложности (Приложение № 6). Во время проведения занятия воспитатель старался привлекать к участию в нем малоактивных детей, не торопил с ответом и давал время подумать, стимулировал выполнение задания детьми с низким и ниже среднего уровнем развития, предоставляя им возможность ответить на более простые вопросы или выполнить более простое задание.

Еще русский педагог К.Д. Ушинский указывал, что наглядность отвечает психологическим особенностям детей, мыслящих "формами, звуками, красками, ощущениями". Наглядность обогащает круг представлений ребенка, делает обучение более доступным, конкретным и интересным, развивает наблюдательность и мышление. Поэтому наглядные и иллюстративные материалы широко используются в воспитательно – образовательной работе с дошкольниками, но это преимущественно занятия по познавательному, речевому развитию и художественно – творческого цикла. Наблюдение за организацией математических занятий показывают, что при их проведении недостаточно эффективное использование наглядности. В средней группе в качестве наглядности применяются в основном геометрические фигуры. Поэтому в процессе экспериментальной деятельности мною применялось большее количество предметов, игрового и иллюстративного материала, рассчитанного на развитие различных сенсорных ощущений для лучшего усвоения и запоминания материала (Приложение № 5, 7). При организации занятий по развитию математических представлений в экспериментальной группе использовалась наряду с натуральной и изобразительной также символическая наглядность.

Кроме вышеперечисленного, в течении всего времени проведения эксперимента большое внимание уделялось стимулированию познавательной активности и самостоятельности детей, сознательному усвоению ими доступных математических понятий.

2.3 Контрольный этап эксперимента

После завершения психолого-педагогического эксперимента мною была проведена повторная диагностика уровня развития математических представлений у детей в экспериментальной т контрольной группах (Приложение № 1, 2) и сопоставлены полученные результаты.

Для этой цели в обеих группах использовались те же методики, что и на констатирующем этапе эксперимента, а также наблюдение за изменениями знаний и умений детей на занятиях и в блоке совместной деятельности с воспитателем. Динамика произошедших изменений отражена в таблицах и диаграммах (Приложение № 8, 9).

В результате сравнительного анализа уровня математического развития детей установлено, что в экспериментальной группе за время проведения эксперимента показатели высокого уровня увеличились на 28% (с 17% до 45%) , тогда как в контрольной группе – только 12% (с17% до 29%) .

Также выявлено, что показатель низкого уровня развития детей в экспериментальной группе уменьшился на 16% (с 25% до 9%) , а в контрольной группе – на 12% (с 25% до 13%).

При изучении диагностических данных по разделам РЭМП можно видеть, что в экспериментальной группе в отличии от контрольной группы за период экспериментальной деятельности по всем разделам наблюдается более значительное улучшение показателей. В экспериментальной группе заметно возрос высокий уровень развития, а изменение низкого уровня близко по показателям к контрольной группе.

Дошкольники экспериментальной группы показали лучшую сформированность общих математических представлений, стали лучше владеть навыками счета,сравнением двух множеств, выраженных смежными числами. У них более развито умение устанавливать равенство и неравенство групп предметов, когда предметы находятся на различном расстоянии друг от друга, когда они различны по величине и т. д. То есть дети экспериментальной группы более приближены к пониманию абстрактного числа.

Кроме того, они используют более разнообразные методы при группировке предметов по признакам, что вырабатывает у детей умение сравнивать, осуществлять логические операции классификации.

В обеих группах – и экспериментальной, и контрольной – у дошкольников сформировались понятия о порядковом и количественном счете, ими освоены такие приемы, как сравнение двух чисел, сопоставление, установление равенства и неравенства их, счет по осязанию, счет на слух и счет различных движений в пределах 5. Но дети экспериментальной группы лучше овладели приемом отсчитывания предметов из большего количества, а также усвоили значение порядковых числительных.

Начало эксперимента Конец эксперимента

Таким образом, в результате теоретического изучения данного вопроса и проведенной практической экспериментальной работы можно сделать вывод о том, что более эффективное и рациональное применение общедидактических принципов в организации и проведении занятий по развитию элементарных математических представлений у дошкольников в детском саду (на примере средней группы), позволяет заметно улучшить качество и продуктивность данной работы.

А это, в свою очередь, приводит к значительному росту показателей уровня развития элементарных математических представлений у детей дошкольного возраста, а также к интеллектуально – познавательному развитию в целом и формированию общей готовности к школе.

Выводы

Таким образом, проведенные теоретические исследования и психолого – педагогический эксперимент позволяют сделать ряд выводов.

Не смотря на то, что общедидактические принципы выступают как основные направляющие положения, возникающие в результате анализа научно – педагогических закономерностей и практического педагогического опыта, и являются главным ориентиром в педагогической работе воспитателя, они недостаточно полно применяются при организации занятий по развитию математических представлений в детском саду.

Хотя математика и является точной наукой, но при ознакомлении с математическими понятиями детей дошкольного возраста принцип наглядности является ничуть не менее действенным, чем принципы научности и системности. Таким образом, современная дидактика исходит из единства чувственного и логического, считает, что наглядность обеспечивает связь между конкретным и абстрактным, содействует развитию абстрактного мышления и во многих случаях служит его опорой.

Но при организации занятий в детском саду нужно помнить, что умелое применение средств наглядности в обучении всецело находится в руках воспитателя. Педагог в каждом отдельном случае должен самостоятельно решать, когда и в какой мере надо применять наглядность в процессе обучения, ибо от этого в определенной степени зависит качество знаний воспитанников.

Учитывая переход современного образования, в том числе и дошкольного, на личностно – ориентированную модель, но сохранение при этом массовости в обучении, особенно актуальным в настоящее время становится наиболее эффективное и продуманное использование в построении занятий принципа индивидуального подхода.

Также в связи с проблемой индивидуального подхода к воспитанникам дошкольного образовательного учреждения в условиях массового обучения привлекает к себе особое внимание принцип доступности в обучении. Слишком упрощенное содержание обучения снижает его развивающие и воспитательные возможности.

В процессе реализации принципа сознательности и активности в развитии элементарных математических представлений у дошкольников необходимо помнить, что при сознательном усвоении знаний формируется творческое отношение к изучению и применению знаний, логическое мышление детей и их мировоззрение. Сознательное усвоение знаний исключает догматическое, при котором воспитанники чисто теоретически воспринимают и механически запоминают преподносимые педагогом знания. Результатом догматического усвоения является формализм знаний, при котором отсутствуют конкретные представления об изучаемых явлениях; запоминание без понимания, без умения творчески применять знания на практике; безынициативность; безошибочно данная формулировка определения того или иного понятия, но без умения им воспользоваться при решении задач.

Активность должна быть деятельным состояние дошкольника в процессе овладения знаниями, которое характеризуется стремлением к учению, умственным напряжением и проявлением волевых усилий в процессе усвоения материала. Такую активность учащихся в обучении называют познавательной активностью, и она является высшей формой активности и сознательности ребенка. Поэтому осуществление в обучении сознательного и активного процесса учения неизбежно формирует такое важное качество личности, как познавательная самостоятельность, которая является важнейшей характеристикой деятельности дошкольника, а впоследствии и школьника в учебном процессе.

Таким образом, объем и прочность знаний, приобретаемых детьми в дошкольном возрасте, во многом обусловливается как задачами начального этапа образования, так и закономерностями процесса обучения, то есть применением в практической деятельности общедидактических принципов.

А это, в свою очередь, позволяет решать не только образовательные, но и воспитательные задачи, закладывая основы гармонично развитой личности.

Литература

1. Белошистая А.В. Почему ребенку трудно изучать математику уже в начальной школе? // Начальная школа – 2004. № 4

2. Воспитание и обучение детей младшего дошкольного возраста / Под ред. Г.Н. Годиной, Э.Г. Пилюгиной – М., 1987.

3. Давайте поиграем: Книга воспитателей детского сада и родителей / Н.И. Касабуцкий, Г.Н. Скобелев, А.А. Столяр, Т.М. Чеботаревская – М., 1991.

4. Ерофеева Т.И., Павлова Л.Н., Новикова В.П. Математика для дошкольников – СПб., 2002.

5. Казанцева Л.С. Дидактические принципы в методике математического развития дошкольников – Ярославль, 2003.

6. Метлина Л.С. Математика в детском саду – М., 1984.

7. Принципы дидактики в преподавании математики / Под ред. К.С. Богут – Киев, 2005.

8. Сай М.К., Удальцова Е.И. Математика в детском саду – Минск, 2000.

9. Сербина Е.В. Математика для малышей – М., 1992.

10. Тарунтаева Т.В. Развитие элементарных математических представлений у дошкольников – М., 1973.

11. Тренинг по психотерапии / Под ред. Т.Д. Зинкевич-Евстигнеевой – СПб., 2006.

12. Усова А.П. Обучение в детском саду – М., 2003.

13. Фидлер М.Я. Математика уже в детском саду – М., 1991.

14. Формирование элементарных математических представлений у дошкольников / Под ред. А.А. Столяр – М., 1988.

15. Щербакова Е.И. Методика обучения математике в детском саду – М., 2000.

16. Ярославцев А.И. Принципы дидактики в педагогической системе К.Д. Ушинского – Ростов, 2002.