Ход урока
.
| Деятельность учителя |
Деятельность ученика |
– Мы завершили изучение большой темы курса стереометрии «Перпендикулярность прямых и плоскостей». Как эта тема у нас появилась?
– Хорошо. В планиметрии мы изучали перпендикулярность прямых. А какие объекты могут быть перпендикулярны в пространстве?
– Да! Поэтому и тема называется «Перпендикулярность прямых и плоскостей».
|
– В планиметрии мы рассматривали различные случаи расположения двух прямых по наличию у них общих точек, в частности перпендикулярность прямых. По аналогии с изучением темы «Параллельность прямых и плоскостей», мы предположили, что аналогичные понятия можно ввести и в стереометрии.
– Перпендикулярными в пространстве могут быть две прямые, прямая и плоскость, две плоскости.
|
– Что же мы изучали в теме «Перпендикулярность прямых и плоскостей»?
– А какие задачи решали?
– Вы видите, какой это обширный материал, сколько в нем разных теорем, задач. На его рассмотрение мы потратили 14 уроков. Что нам предстоит сделать теперь?
– А что значит привести знания в систему?
– Правильно. А как будет звучать тема сегодняшнего урока?
– Хорошо. Цели мы уже сформулировали. Запишем тему.
|
–Определения перпендикулярности различных объектов, доказывали признаки и свойства перпендикулярности, способы нахождения расстояний и углов между прямыми, прямой и плоскостью, плоскостями.
– Доказывали перпендикулярность объектов, находили соответствующие расстояния и углы.
– Привести полученные знания и умения в систему и подготовиться к контрольной работе.
– Выделить основные понятия, установить взаимосвязь между ними, а также выделить основные типы задач и методы их решения.
– Перпендикулярность прямых и плоскостей.
|
– Перпендикулярность каких объектов мы изучили?
– Будем работать с таблицей.
< Открывает заголовок таблицы 1>
– Итак, в теме мы выделили три блока, связанные с перпендикулярностью. Вспомним, определение перпендикулярности каждой пары объектов и выделим способ доказательства перпендикулярности каждой пары. Какие прямые называются перпендикулярными?
– Как могут быть расположены перпендикулярные прямые в пространстве? < Открывает соответствующий рисунок>
– Какой теоретический факт, связанный с перпендикулярностью прямых мы изучали?
Реклама

– Сформулируйте ее. < Открывает рисунок>
– Поговорим о перпендикулярности прямой и плоскости. Начнем с определения.
< Открывает рисунок>
– В этой части было доказано много теорем, подумайте, какие теоремы вы бы отнесли к ней. Называйте и формулируйте их.
<Открывает соответствующие рисунки>
– В эту часть мы отнесем теорему о трех перпендикулярах и обратную к ней.
А как вы думаете почему?
–Молодец! Рассмотрим последнюю часть. Какие две плоскости называются перпендикулярными?
–Какие факты можно отнести в эту часть?
– Правильно. Итак, тема «Перпендикулярность прямых и плоскостей» появилась по аналогии с темой «Перпендикулярность прямых на плоскости». Я напомню вам, что многие определения и теоремы вы формулировали сами по аналогии с известными определениями в планиметрии или обобщая их – заменяя прямые на плоскости, лучи на полуплоскости. При доказательстве теорем в каждом последующем блоке использовались теоремы предыдущего блока <показывает столбцы> и теоретические положения темы «Параллельность прямых и плоскостей». Однако и перпендикулярность работает на параллельность – мы получили новые свойства и признаки параллельности прямых и параллельности плоскостей. Посмотрите на рисунки 7 и 8. Например, сформулируйте признак параллельности прямых по рисунку 7.
–Хорошо. Продолжите предложение: «Две прямые в пространстве перпендикулярны, если …».
<Аналогичная работа проводится для оставшихся двух случаев>
|
– Перпендикулярность прямых, прямой и плоскости, двух плоскостей.
– Две прямые в пространстве называются перпендикулярными, если угол между ними равен 900
.
– Они могут пересекаться и скрещиваться.
– Лемму о перпендикулярности двух параллельных прямых третьей.
<Формулируют>
– Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
– Признак перпендикулярности прямой и плоскости <формулирует>.
– Теорема о связи между параллельностью прямых и их перпендикулярностью к плоскости <формулирует>.
– Теорема о связи между параллельностью двух плоскостей и их перпендикулярностью к прямой <формулирует>.
– Потому что она доказывается с помощью определения прямой перпендикулярной к плоскости.
– Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен 900
.
–Признак перпендикулярности двух плоскостей.
- Две прямые в пространстве параллельны, если они перпендикулярны некоторой плоскости.
Реклама

Две прямые в пространстве перпендикулярны, если
- одна из них перпендикулярна некоторой прямой, а другая ей параллельна;
- одна из них перпендикулярна некоторой плоскости, а другая лежит в этой плоскости;
- одна из них является наклонной к некоторой плоскости, а другая лежит в этой плоскости и перпендикулярна проекции первой прямой.
<Ученики формулируют следующие эвристики:
Прямая и плоскость в пространстве перпендикулярны, если
- прямая перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости;
- прямая параллельна некоторой другой прямой, перпендикулярной данной плоскости;
- данная плоскость параллельна некоторой другой плоскости, перпендикулярной данной прямой.
Две плоскости перпендикулярны, если одна из этих плоскостей содержит прямую, перпендикулярную второй плоскости. >
|
–Давайте теперь поработаем с задачей. Рассмотрим следующую конфигурацию: дан равносторонний треугольник АВС, через середину О стороны АВ проведен перпендикуляр ОD к плоскости АВС, построены отрезки DА, DВ, DС, ОС. Запишем что дано. Задание 1: найдите пары перпендикулярных прямых, прямой и плоскости, двух плоскостей, выделите теоретический базис доказательства.
– Работаем в парах. Первый ряд ищет пары перпендикулярных прямых, второй – перпендикулярных прямой и плоскости, третий ряд – пары перпендикулярных плоскостей. Даю вам 5 минут.
– Начнем с первого ряда. Делайте записи в тетради. <Записи на доске делает ученик>
–Хорошо. Послушаем теперь второй ряд.
–Третий ряд, пожалуйста.
|
<Работают>
< Ученики называют по одной найденной паре по очереди, называя то положение, которое использовали>
– DO^AB (DO^ABC, значит, по определению прямой, перпендикулярной плоскости , DO, в частности, перпендикулярно АВ)
– DO^AC, DO^BC (аналогично)
– DC^AB(по лемме, теореме о трех перпендикулярах, лемме).
–DO^ABC(по условию).
–AB^COD,CO^ADB(по признаку перпендикулярности прямой и плоскости).
–DAB^ABC (по признаку перпендикулярности плоскостей)
–DOC^ABC (по признаку перпендикулярности плоскостей)
–DOC^ADB (по признаку перпендикулярности плоскостей).
|
| – Мы знаем, что изученная тема позволяет ввести метрические характеристики пространства: расстояния между объектами и углы между ними. |
Давайте повторим, как определяются расстояния между различными фигурами. <Открывает заголовок: «Расстояния в пространстве»>
<Учитель открывает по очереди каждый рисунок в таблице>
–Что называется расстоянием от точки до прямой?
–Какие еще расстояния можете назвать?
– Вспомните, как мы решали задачи о нахождении расстояний.
– То есть решение таких задач сводилось всегда к решению треугольников, поэтому отметим это в таблице.
– Теперь вспомним, какие углы мы рассматривали.<Открывает заголовок: «Углы в пространстве»>
– Опишите это понятие.
<Открывает соответствующий рисунок>
– Какие еще углы вы знаете?
– Решение задач на нахождение углов тоже сводится к решению треугольников.
|
– Расстоянием от точки до прямой называется длина перпендикуляра, проведенного от этой точки к данной прямой.
– От точки до плоскости. Это длина перпендикуляра, проведенного изданной точки к данной плоскости.
– Расстояние между параллельными прямыми. Это расстояние от произвольной точки одной прямой до другой.
– Между параллельными прямой и плоскостью. Это расстояние от произвольной точки прямой до плоскости.
– Между параллельными плоскостями – расстояние от произвольной точки одной из плоскостей к другой.
– Между скрещивающимися прямыми– расстояние между одной из этих прямых и плоскостью, проведенной через другую прямую параллельно первой.
– Сначала мы строили отрезок, длина которого равна искомому расстоянию. Затем включали его в треугольник.
– Угол между прямыми.
– Если прямые пересекаются, то углом между ними называется наименьший из углов, образованных при их пересечении. Если прямые скрещиваются, то надо провести прямые, параллельные данным через произвольные точки пространства и искать угол между ними.
– Угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярную к ней – это угол между прямой и ее проекцией на эту плоскость.
– И угол между плоскостями – это наименьший двугранный угол, образованный при их пересечении.
|
– Вернемся к задаче. Найдите углы наклона прямых DA, DB, DC к плоскости ABC. Будем использовать тот же рисунок. Две минуты вам на размышление.
– Начнем с первого задания.
– Как вычислять угол мы только поговорим, а вычисления сделаете дома. Продолжай.
–Второй ряд, пожалуйста.
–И последний угол?
–Дорешаете дома.
–Следующее задание. Найдите расстояния от т.D до пл. АВС, от С до АDВ, от А до DОС. Работаем по рядам и по тому же рисунку.
–Отлично! Теперь найдите расстояния от точки D до прямых АВ, ВС, АС.
Эту задачу будем решать на новом рисунке.
–Итак, начнем.
–Далее. Прежде чем вычислять, нужно правильно построить искомый отрезок. Пусть кто-нибудь выйдет к доске и построит его.
– Мы не знаем как изобразить перпендикуляр из точки D до прямой ВС. В какой еще плоскости расположена прямая ВС?
– Чем является искомая прямая по отношению к этой плоскости?
– То есть прямая ВС должна быть перпендикулярна к наклонной. Что отсюда следует?
– А через какую точку пройдет проекция наклонной?
– Значит нужно сначала изобразить перпендикуляр из точки О к прямой ВС. Можем ли мы это сделать?
– А если бы мы и о треугольнике АВС ничего не знали, то как бы изобразили перпендикуляр из точки D к прямой ВС?
– Как найти DК?
– Как найти расстояние от D до АС? Постройте его на доске.
– Найдите линейные углы двугранных углов при ребрах АС и ВС. Это задача №7.
– Назовите их и докажите.
–Как их найти?
|
– Так как ОD^АВС, то АО – проекция наклонной АD на плоскость АВС, следовательно ÐDАО – угол между DА и АВС.
– Его можно найти из прямоугольного треугольника АОD: DО дано, а АО равно половине АВ.
–Угол между DВ и АВС – это ÐDВО.
–Угол между DС и АВС – это ÐDСО.
– Так как DО – перпендикуляр, проведенный из точки D к плоскости АВС, то DО – искомое расстояние.
– Мы доказывали, что СО^DАВ, значит СО–расстояние от С до DАВ.
–АВ^DОС, то АО–расстояние от А до DОС.
Так как DО перпендикулярно АВ, то DО – расстояние между D и прямой АВ.
–АВС.
– Наклонной.
– Она должна быть перпендикулярной к проекции.
– Через точку О, так как она проекция точки D.
– Да. Сначала построим перпендикуляр к ВС, проходящий через точку А. Пусть М–середина ВС, тогда АМ – медиана правильного ∆АВС, а, следовательно, и высота. Проведем ОК параллельно АМ, тогда ОК^ВС, и ОК–проекция DК на АВС. При этом DК^ВС (по теореме о трех перпендикулярах). Поэтому DК–расстояние от точки D до прямой ВС.
– Произвольно.
– Его можно найти из треугольника DОК. DО известно, ОК равно половине АМ, так как ОК – средняя линия ∆АМВ.
– Аналогично, причем DL равно DК.
– Они уже построены.
–ÐDКО – линейный угол двугранного угла при ребре ВС (по определению), так как ОК перпендикулярна ВС и DК перпендикулярна ВС. Аналогично, ÐDLО – линейный угол двугранного угла при ребре АС.
– Например, ÐDКО можно найти из прямоугольного треугольника DОК. А угол DLO равен углу DКО.
|
– Это все задания, которые мы планировали решить на уроке.
– А теперь подведем итоги сегодняшней работы. Мы говорили о понятии перпендикулярности в пространстве. Сказали, что перпендикулярными могут быть две прямые, прямая и плоскость, две плоскости.
– Какие типы задач нами были рассмотрены?
–Как вы думаете какое значение имеет данная тема в курсе стереометрии?
|
–на доказательство перпендикулярности объектов, задачи на нахождение расстояния от точки до прямой, от точки до плоскости, задачи на нахождение углов между прямой и плоскостью, между плоскостями.
–позволяет ввести метрические характеристики пространства, то есть определение углов и расстояний между основными фигурами.
|
– Что вы теперь умеете делать?
– Необходимо помнить, что каждое построение нужно обосновать прежде, чем проводить вычисления.
|
– Мы умеем доказывать перпендикулярность прямых, прямой и плоскости, двух плоскостей; решать основные задачи на вычисление расстояний и углов, как то находить расстояние от точки до прямой и от точки до плоскости, находить углы между прямой и плоскостью, между плоскостями. |
| Дома оформить решение последней задачи и подготовиться к контрольной работе. |
Расстояния в пространстве
(Таблица 1)
| От точки до прямой
|
Между параллельными прямыми
|
От точки до плоскости
|
Между парал
–
лельными прямой и плоскостью
|
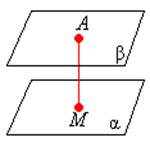
Между параллельными плоскостями
|
Между скрещивающимися прямыми
|
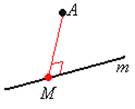
|
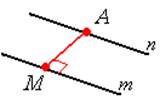
|
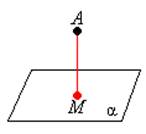 AM
^ α AM
^ α
|
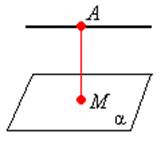
AM
^ α
|
AM
^ β
|
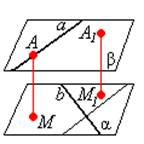
AM
^ β
|
| Решение треугольников
|
Углы в пространстве
| Между прямыми
|
Между наклонной к плоскости и плоскостью
|
Между плоскостями
|
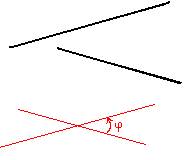
0°< φ
≤ 90°
|
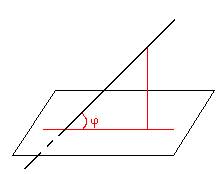
0°< φ
< 90°
|
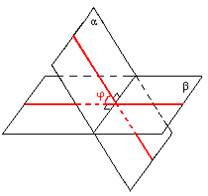
0°< φ
≤ 90°
|
| Решение треугольников
|
Перпендикулярность прямых и плоскостей
Перпендикулярные
прямые
|
Перпендикулярные прямая и плоскость
|
Перпендикулярные
плоскости
|
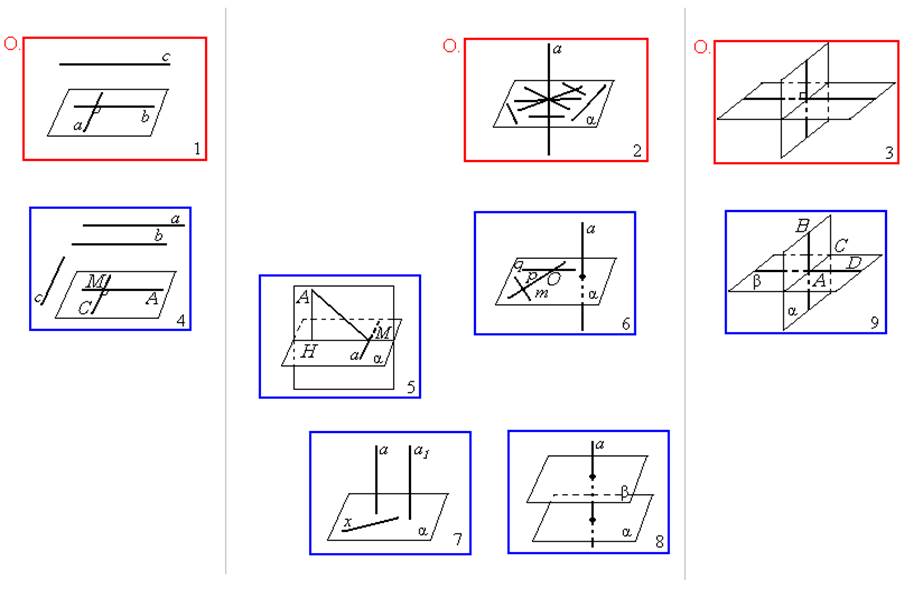
Записи на доске и в тетрадях
Перпендикулярность прямых и плоскостей
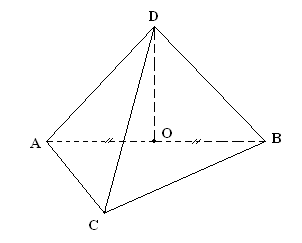
Дано: ∆АВС - равносторонний,
О - середина АВ,
ОD^ АВС.
АВ=6см, ОD=3см.
1. Найти пары перпендикулярных прямых
.
Решение.
а) DO^AB, DO^AC, DO^BC (по определению прямой, перпендикулярной плоскости).
б) DC^AB (по лемме, теореме о трех перпендикулярах, лемме).
2. Найти пары перпендикулярных прямой и плоскости
.
Решение.
а) DO^ABC(по условию).
б)AB^COD, CO^ADB(по признаку перпендикулярности прямой и плоскости).
3. Найти пары двух плоскостей
.
Решение.
DAB^ABC, DOC^АВС, DOC^ADB (по признаку перпендикулярности плоскостей).
4.Найти углы между
DA,
DB,
DC и плоскостью
ABC
.
Решение.
Так как ОD^АВС, то АО – проекция наклонной АD на плоскость АВС, следовательно ÐDАО – угол между DА и АВС.
5. Найдите расстояния от т.
D
до плоскости АВС, от С до А
D
В, от А до
D
ОС
.
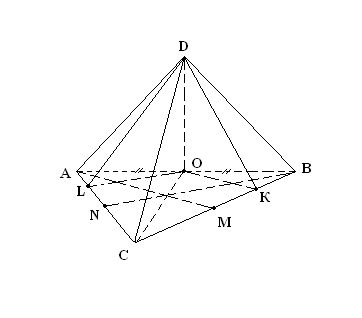 6. Найдите расстояния от точки
D
до прямых АВ, ВС, АС
. 6. Найдите расстояния от точки
D
до прямых АВ, ВС, АС
.
|