ОГЛАВЛЕНИЕ
Введение
Глава 1. Теоретические основы формирования представления о функциональной зависимости у младших школьников
1.1 Понятие «функциональная зависимость» в психолого-педагогической литературе
1.2 Педагогические идеи преподавания функциональной зависимости в начальной школе
1.3 Виды упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников
Глава 2. Опытно-экспериментальная работа по формированию представлений о функциональной зависимости у младших школьников с применением комплекса упражнений
2.1. Диагностика уровней сформированности представлений младших школьников о функциональной зависимости
2.2. Реализация комплекса упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников
Заключение
Библиография
Приложения
Введение
Понятие функциональной зависимости является одним из ведущих в математической науке, поэтому сформированность представлений понятия у младших школьников представляет важную задачу в целенаправленной деятельности учителя по развитию математического мышления и творческой активности детей. Развитие функционального мышления предполагает, прежде всего, развитие способности к обнаружению новых связей, овладению общими учебными приемами и умениями.
Формирование представления о функциональной зависимости способствует формированию мыслительных операций и воспитанию интеллектуальных качеств личности. Направления подобной работы выражаются в характере задач, предлагаемых учащимся. Материал начального математического курса содержит достаточное количество примеров, на которых можно разъяснить зависимость одной величины от другой. К ним, в частности, относятся: задачи на составление и решение уравнений, оптимизационные и комбинаторные задачи, задачи с величинами, находящимися в прямой и обратной зависимости, задачи с использованием таблиц, числовой оси и координатной плоскости.
Все это и обусловило актуальность темы исследования.
При изучении психолого-педагогической литературы нами было выявлено противоречие между необходимостью формирования представлений младших школьников о функциональной зависимости и малым количеством разработок по технологии педагогической организации этого процесса в начальной школе.
Реклама

Выявленное противоречие позволило обозначить проблему исследования: изучение возможностей комплекса упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников.
Данная проблема позволила сформулировать тему исследования: «Комплекс упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников».
Объект исследования: процесс формирования представлений о функциональной зависимости у младших школьников.
Предмет исследования: комплекс упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников.
Цель исследования: теоретически выявить и путем опытно-экспериментальной работы проверить эффективность комплекса упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников.
Изучение психолого-педагогической литературы по теме исследования позволило выдвинуть следующую гипотезу: предполагается, что формирование представлений о функциональной зависимости у младших школьников будет успешнее при использовании специально подобранного комплекса упражнений.
В соответствии с целью и гипотезой исследования были определены следующие задачи:
1. Проанализировать методическую литературу по проблеме исследования.
2. Рассмотреть понятие «функциональная зависимость» в психолого-педагогической литературе.
3. Исследовать педагогические идеи преподавания функциональной зависимости в начальной школе.
4. Экспериментальным путем проверить эффективность комплекса упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников.
Теоретико-методологическая основа исследования: методические и научные исследования формирования функциональной зависимости в трудах М.А. Бантовой, Л.Г. Петерсон, Е.Д. Цыдыповой, системный подход, принцип ведущей роли обучения в развитии, теория поэтапного формирования умственных действий П.Я. Гальперинп, Н.Ф.Талызиной, теория о структуре учебной деятельности Д.Б. Эльконина, В.В. Давыдова, методическая концепция развивающего обучения математике в 1-4 классах Н.Б.Истоминой и других.
- Для решения поставленных задач и проверки гипотезы были использованы следующие методы исследования:
- теоретические: анализ психолого-педагогической, дидактической, методической, научно-методической литературы и документов по проблемам формирования представления функциональной зависимости; анализ изучения функционального материала в теории и практике обучения математике в начальной школе.
Реклама

- экспериментальные: анкетирование, тестирование, наблюдение, беседы с учителями и учащимися, констатирующий, формирующий и сравнительный эксперименты, экспериментальное преподавание (организация учебной деятельности учащихся 3 классов, направленной на подготовку к формированию представлений функциональной зависимости посредством комплекса упражнения), статистические методы интерпретации данных эксперимента.
Опытно-экспериментальная база исследования: МОУ СОШ №31 города Ишима. В эксперименте участвовали учащиеся 3 «А» и 3 «Б» классов.
Исследование проводилось в три этапа.
Первый этап – постановочный (01.02.10 – 01.03.10) – выбор и осмысление темы. Изучение психолого-педагогической литературы, постановка проблемы, формулировка цели, предмета, объекта, задач исследования, постановка гипотезы.
Второй этап – собственно-исследовательский (02.03.10 – 02.04.10) – разработка комплекса мероприятий и их систематическое проведение, обработка полученных результатов, проверка гипотезы.
Третий этап – интерпретационно-оформительский (03.04.10 – 03.05.10) – обработка и систематизация материала.
Научная новизна исследования: исследования состоит в том, что представления о функциональной зависимости младших школьников впервые рассматривается как самостоятельная исследовательская проблема; экспериментально проверена эффективность комплекса упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников.
Практическая значимость заключается в том, что выводы и результаты курсовой работы могут быть использованы в учебно-воспитательном процессе общеобразовательных учреждений.
Структура и объем работы: работа состоит из введения, двух глав, заключения, библиографического списка, включающего 37 наименований, приложения. Работа включает таблицы (6), иллюстрирована рисункам (3). Общий объем работы 50 страниц компьютерного текста.
Глава 1. Теоретические основы формирования представления о функциональной зависимости у младших школьников
1.1
Понятие «функциональная зависимость» в психолого-педагогической литературе
Начиная с XVII в. одним из важнейших понятий является понятие функции. Оно сыграло и поныне играет большую роль в познании реального мира.
Идея функциональной зависимости восходит к древности, она содержится уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами, в первых формулах для нахождения площади и объема тех или иных фигур.
Те вавилонские ученые, которые 4-5 тысяч лет назад нашли для площади S круга радиусом r формулу S=3r2 (грубо приближенную), тем самым установили, пусть и не сознательно, что площадь круга является функцией от его радиуса. Таблицы квадратов и кубов чисел, также применявшиеся вавилонянами, представляют собой задания функции [13, с.117].
Однако явное и вполне сознательное применение понятия функции и систематическое изучение функциональной зависимости берут свое начало в XVII в. в связи с проникновением в математику идеи переменных. В “Геометрии” Декарта и в работах Ферма, Ньютона и Лейбница понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями: ординаты точек кривых - функции от абсцисс (х); путь и скорость - функции от времени (t) и тому подобное [13, с.117].
Четкого представления понятия функции в XVII в. еще не было, путь к первому такому определению проложил Декарт, который систематически рассматривал в своей “Геометрии” лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться таким образом с понятием аналитического выражения - формулы.
Слово “функция” (от латинского functio - совершение, выполнение) Лейбниц употреблял с 1673 г. в смысле роли (величина, выполняющая ту или иную функцию). Как термин в нашем смысле выражение “функция от х” стало употребляться Лейбницем и И. Бернулли; начиная с 1698 г. Лейбниц ввел также термины “переменная” и “константа” (постоянная). Для обозначения произвольной функции от х Иоганн Бернулли применял знак j х, называя j характеристикой функции, а также буквы х или e; Лейбниц употреблял х1, х2 вместо современных f1(x), f2(x). Эйлер обозначал через f : х, f : (x + y) то, что мы ныне обозначаем через f (x), f (x + y). Наряду с j Эйлер предлагает пользоваться и буквами F, Y и прочими. Даламбер делает шаг вперед на пути к современным обозначениям, отбрасывая эйлерово двоеточие; он пишет, например, j t, j (t + s) [2, с.109].
Явное определение функции было впервые дано в 1718 г. одним из учеников и сотрудников Лейбница, выдающимся швейцарским математиком Иоганном Бернулли: “Функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных” [21, с.44].
Леонард Эйлер во “Введении в анализ бесконечных” (1748) примыкает к определению своего учителя И. Бернулли, несколько уточняя его. Определение Л. Эйлера гласит: “Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств”. Так понимали функцию на протяжении почти всего XVIII в. Даламбер, Лагранж и другие видные математики. Что касается Эйлера, то он не всегда придерживался этого определения; в его работах понятие функции подвергалось дальнейшему развитию в соответствии с запросами математической науки. В некоторых своих произведениях Л. Эйлер придает более широкий смысл функции, понимая ее как кривую, начертанную “свободным влечением руки”. В связи с таким взглядом Л. Эйлера на функцию между ним и его современниками, в первую очередь его постоянным соперником, крупным французским математиком Даламбером, возникла большая полемика вокруг вопроса о возможности аналитического выражения произвольной кривой и о том, какое из двух понятий (кривая или формула) следует считать более широким. Так возник знаменитый спор, связанный с исследованием колебаний струны [19, с.123].
В “Дифференциальном исчислении”, вышедшем в свет в 1755 г, Л. Эйлер дает общее определение функции: “Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых”. “Это наименование, - продолжает далее Эйлер, - имеет чрезвычайно широкий характер; оно охватывает все способы, какими одно количество определяется с помощью других”. На основе этого определения Эйлера французский математик С. Ф. Лакруа в своем “Трактате по дифференциальному и интегральному исчислению”, опубликованном в 1797 г., смог записать следующее: “Всякое количество, значение которого зависит от одного или многих других количеств, называется функцией этих последних независимо от того, известно или нет, какие операции нужно применить, чтобы перейти от них к первому” [2, с.112].
Как видно из этих определений, само понятие функции фактически отождествлялось с аналитическим выражением. Новые шаги в развитии естествознания и математики в XIX в. вызвали и дальнейшее обобщение понятия функции.
Большой вклад в решение спора Эйлера, Даламбера, Д. Бернулли и других ученых XVIII в. по поводу того, что следует понимать под функцией, внес французский математик Жан Батист Жозеф Фурье (1768-1830), занимавшийся в основном математической физикой. В представленных им в Парижскую Академию наук в 1807 и 1811 гг., работах по теории распространения тепла в твердом теле Фурье привел и первые примеры функций, которые заданы на различных участках различными аналитическими выражениями.
Из трудов Фурье явствовало, что любая кривая независимо от того, из скольких и каких разнородных частей она составлена, может быть представлена в виде единого аналитического выражения и что имеются также прерывные кривые, изображаемые аналитическим выражением. В своем “Курсе алгебраического анализа”, опубликованном в 1821 г., французский математик О. Коши обосновал выводы Фурье. Таким образом, на известном этапе развития физики и математики стало ясно, что приходится пользоваться и такими функциями, для определения которых очень сложно или даже невозможно ограничиться одним лишь аналитическим аппаратом. Последний стал тормозить требуемое математикой и естествознанием расширение понятия функции [21, с.47].
В 1834 г. в работе “Об исчезании тригонометрических строк” Н. И. Лобачевский, развивая вышеупомянутое эйлеровское определение функции в 1755 г., писал: “Общее понятие требует, чтобы функцией от х называть число, которое дается для каждого х и вместе с х постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подает средство испытывать все числа и выбирать одно из них; или, наконец, зависимость может существовать и оставаться неизвестной... Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа, одни с другими в связи, принимать как бы данными вместе” [20, с.110].
Еще до Лобачевского аналогичная точка зрения на понятие функции была высказана чешским математиком Б. Больцано. В 1837 г. немецкий математик П. Лежен-Дирихле так сформулировал общее определение понятия функции: “у есть функция переменной х (на отрезке a £ х £ b), если каждому значению х (на этом отрезке) соответствует совершенно определенное значение у, причем безразлично, каким образом установлено это соответствие - аналитической формулой, графиком, таблицей либо даже просто словами” [14, с.332].
Таким образом, примерно в середине XIX в. после длительной борьбы мнений понятие функции освободилось от уз аналитического выражения, от единовластия математической формулы. Главный упор в новом общем определении понятия функции делается на идею соответствия.
Во второй половине XIX в. после создания теории множеств в понятие функции, помимо идеи соответствия, была включена и идея множества. Таким образом, в полном своем объеме общее определение понятия функции формулируется следующим образом: если каждому элементу х множества А поставлен в соответствие некоторый определенный элемент у множества В, то говорят, что на множестве А задана функция у = f (х), или что множество А отображено на множество В. В первом случае элементы х множества А называют значениями аргумента, а элементы у множества В - значениями функции; во втором случае х - прообразы, у - образы. В современном смысле рассматривают функции, определенные для множества значений х, которые, возможно, и не заполняют отрезка a £ x £ b, о котором говорится в определении Дирихле. Достаточно указать, например, на функцию-факториал y = n , заданную на множестве натуральных чисел. Общее понятие функции применимо, конечно, не только к величинам и числам, но и к другим математическим объектам, например к геометрическим фигурам. При любом геометрическом преобразовании (отображении) мы имеем дело с функцией.
Общее определение функций по Дирихле сформировалось после длившихся целый век дискуссий в результате значительных открытий в физике и математике в XVIII и первой половине XIX в. Дальнейшее развитие математической науки в XIX в. основывалось на этом определении, ставшим классическим. Но уже с самого начала XX в. это определение стало вызывать некоторые сомнения среди части математиков. Еще важнее была критика физиков, натолкнувшихся на явления, потребовавшие более широкого взгляда на функцию. Необходимость дальнейшего расширения понятия функции стала особенно острой после выхода в свет в 1930 г. книги “Основы квантовой механики” Поля Дирака, крупнейшего английского физика, одного из основателя квантовой механики. Дирак ввел так называемую дельта-функцию, которая выходит далеко за рамки классического определения функции. В связи с этим советский математик Н. М. Гюнтер и другие ученые опубликовали в 30-40-х годах нашего столетия работы, в которых неизвестными являются не функции точки, а “функции области”, что лучше соответствует физической сущности явлений [16, с.113].
В общем виде понятие обобщенной функции было введено французом Лораном Шварцем. В 1936 г. 28-летний советский математик и механик Сергей Львович Соболев первым рассмотрел частный случай обобщенной функции, включающей и дельта-функцию, и применил созданную теорию к решению ряда задач математической физики. Важный вклад в развитие теории обобщенных функций внесли ученики и последователи Л. Шварца - И.М. Гельфанд, Г.Е. Шилов и другие.
Прослеживая исторический путь развития понятия функции, невольно приходишь к мысли о том, что эволюция еще далеко не закончена и, вероятно, никогда не закончится, как никогда не закончится и эволюция математики в целом. Новые открытия и запросы естествознания и других наук приведут к новым расширениям понятия функции и других математических понятий. Математика - незавершенная наука, она развивалась на протяжении тысячелетий, развивается в нашу эпоху и будет развиваться в дальнейшем.
Обоснование функциональной линии как ведущей для школьного курса математики — одно из крупнейших достижений современной методики. Однако реализация этого положения может быть проведена многими различными путями; многообразие путей вызвано фундаментальностью самого понятия функции.
Для того чтобы составить представление об этом многообразии, сравним две наиболее резко различающиеся методические трактовки этого понятия; первую мы назовем генетической, а вторую — логической.
Генетическая трактовка понятия функции основана на разработке и методическом освоении основных черт, вошедших в понятие функции до середины XIX в. Наиболее существенными понятиями, которые при этой трактовке входят в систему функциональных представлений, служат переменная величина, функциональная зависимость переменных величин, формула (выражающая одну переменную через некоторую комбинацию других переменных), декартова система координат на плоскости.
Генетическое развертывание понятия функции обладает рядом достоинств. В нем подчеркивается «динамический» характер понятия функциональной зависимости, легко выявляется модельный аспект понятия функции относительно изучения явлений природы. Такая трактовка естественно увязывается с остальным содержанием курса алгебры, поскольку большинство функций, используемых в нем, выражаются аналитически или таблично.
Генетическая трактовка понятия функции содержит также черты, которые следует рассматривать как ограничительные. Одним из очень существенных ограничений является то, что переменная при таком подходе всегда неявно (или даже явно) предполагается пробегающей непрерывный ряд числовых значений. Поэтому в значительной степени понятие связывается только с числовыми функциями одного числового аргумента (определенными на числовых промежутках). В обучении приходится, используя и развивая функциональные представления, постоянно выходить за пределы его первоначального описания [18, с.234].
Логическая трактовка понятия функции исходит из положения о том, что строить обучение функциональным представлениям следует на основе методического анализа понятия функции в рамках понятия алгебраической системы. Функция при таком подходе выступает в виде отношения специального вида между двумя множествами, удовлетворяющего условию функциональности. Начальным этапом изучения понятия функции становится вывод его из понятия отношения.
Реализация логического подхода вызывает необходимость иллюстрировать понятие функции при помощи разнообразных средств; язык школьной математики при этом обогащается. Помимо формул и таблиц, здесь находят свое место задание функции стрелками, перечислением пар, использование не только числового, но и геометрического материала; геометрическое преобразование при таком подходе оказывается возможным рассматривать как функцию. Обобщенность возникающего понятия и вытекающие отсюда возможности установления разнообразных связей в обучении математике — основные достоинства такой трактовки.
Однако выработанное на этом пути общее понятие оказывается в дальнейшем связанным главным образом с числовыми функциями одного числового аргумента, т. е. с той областью, в которой оно гораздо проще формируется на генетической основе.
Таким образом, если генетический подход оказывается недостаточным для формирования функции как обобщенного понятия, то логический обнаруживает определенную избыточность. Отметим, что различия в трактовках функции проявляются с наибольшей резкостью при введении этого понятия. В дальнейшем изучении функциональной линии различия постепенно стираются, поскольку изучается в курсах алгебры и начал анализа не само понятие функции, а в основном конкретно заданные функции и классы функций, их разнообразные приложения в задачах естествознания и общественного производства.
В современном школьном курсе математики в итоге длительных методических поисков в качестве ведущего был принят генетический подход к понятию функции. Одновременно учитывается все ценное, что можно извлечь из логического подхода. Исходя из этого при формировании понятий и представлений, методов и приемов в составе функциональной линии система обучения строится так, чтобы внимание учащихся сосредоточивалось, во-первых, на выделенных и достаточно четко разграниченных представлениях, связанных с функцией, и, во-вторых, на установлении их взаимодействия при развертывании учебного материала. Иными словами, в обучении должна быть выделена система компонентов понятия функции и установлена связь между ними. В эту систему входят такие компоненты:
- представление о функциональной зависимости переменных величин в реальных процессах и в математике;
- представление о функции как о соответствии;
- построение и использование графиков функций, исследование функций;
- вычисление значений функций, определенных различными способами.
В процессе обучения математике все указанные компоненты присутствуют при любом подходе к понятию функции, но акцент может быть сделан на одном из них. Как только что мы отметили, функциональный компонент является основой введения и изучения понятия функции. На этой основе при организации работы над определением вводятся и другие компоненты, проявляющиеся в различных способах задания функциональной зависимости и ее графического представления [1, с.215].
Функциональная зависимость - форма устойчивой взаимосвязи между объективными явлениями или отражающими их величинами, при которой изменение одних явлений вызывает определенное количественное изменение др. Объективно функциональная зависимость проявляется в виде законов и отношений, обладающих точной количественной определенностью. Они могут быть в принципе выражены в виде уравнений, объединяющих данные величины или явления как функцию и аргумент. Функциональная зависимость может характеризовать связь:
1) между свойствами и состояниями материальных объектов и явлений;
2) между самими объектами, явлениями или же материальными системами в рамках целостной системы более высокого порядка;
3) между объективными количественными законами, находящимися в отношении субординации, в зависимости от их общности и сферы действия;
4) между абстрактными математическими величинами множествами, функциями или структурами, безотносительно к тому, что они выражают. Функциональная зависимость предполагает, что явления, подчиняющиеся ей, характеризуются через определенные параметры, константы, конкретные условия, количественные законы. Функциональная зависимость не тождественна причинной связи. Наряду с явлениями, в которых причинная связь выражается через объективные функциональные отношения, существуют и функциональная зависимость между свойствами тел или математическими величинами, не являющиеся причинными связями [2, с.113].
Таким образом, понятие функции выступает в курсе математики как определённая математическая модель, что и является мотивировкой для его углублённого изучения. Функциональная зависимость – это зависимости одной переменной от другой. Функциональная зависимость двух количественных признаков или переменных состоит в том, что каждому значению одной переменной всегда соответствует одно определенное значение другой переменной.
В следующем параграфе мы рассмотрим особенности представлений о функциональной зависимости у младших школьников.
1.2
Педагогические идеи преподавания функциональной зависимости в начальной школе
В течение нескольких столетий понятие функции изменялось и совершенствовалось. Необходимость изучения функциональной зависимости в школьном курсе математики начальной школы была в центре внимания педагогической печати уже со второй половины XIX века. Большое внимание этому вопросу уделили в своих работах такие известные методисты, как М. В. Остроградский, В. Н. Шкларевич, С. И. Шохор-Троцкий, В. Е. Сердобинский, В. П. Шереметевский.
Первый этап - этап введения понятия функции (в основном, через аналитическое выражение) в школьный курс математики. Например, в учебнике Н. Ш Фусса "Начальные основания чистой математики" в разделе "Основания дифференциального и интегрального исчислений" приводилось следующее определение: "Функцией переменной величины называется выражение, состоящее из сей переменной, соединенной с постоянными величинами" [7, с.220].
На собрании комиссии преподавания математики отдела обучения Московского Общества распространения технических знаний В.П. Шереметевский и В.Я. Сердобинский представили радикальное решение проблемы введения функциональной зависимости в школьную математику в виде рекомендации "построения курса школьной математики на основе идеи функциональной зависимости". Математическая комиссия, функционировавшая в 1900 г. в Министерстве Народного Образования, предусмотрела идею включения в программу функциональной зависимости в связи с изучением элементов аналитической геометрии. Эти предложения начали осуществляться с 1903 г. при обучении математике в Кадетском корпусе, а с 1907 г. - в выпускных классах реальной школы.
Второй этап введения понятия функции в курс начальной школы характеризуется в основном переходом к графическому изображению функциональной зависимости и расширением круга изучаемых функций.
На Международном конгрессе в Риме в 1908 г. Ф. Клейн изложил основные принципы в решении вопроса о месте и роли понятия функции в школьной математике: "Мы..., стремимся положить в основу преподавания понятие функции, ибо это есть то понятие, которое в течение последних двухсот лет заняло центральное место всюду, где только мы встречаем математическую мысль. Это понятие мы желаем выработать при преподавании столь рано, как это только возможно, постоянно применяя графический метод изображения каждого закона в системе координат (хОу), которая теперь употребляется при всяком практическом применении математики». Истинное значение имеет предложение Ф. Клейна о введении общего понятия функции не в форме абстрактного понятия, а на конкретных примерах, которые «...сделали бы это понятие живым достоянием ученика, но непременно это понятие, как фермент, должно проникнуть во все преподавание математики в средней школе" [19, с.124].
Активное участие в борьбе за реформу математического образования приняли передовые русские преподаватели математики. Функциональная зависимость нашла свое отражение в новых программах по математике. Большое внимание вопросам, связанным с идеей функциональной зависимости, уделили два Всероссийских съезда преподавателей математики, созванных в 1911 г. (г. Санкт-Петербург) и 1913 г. (г. Москва).
После съездов в 1911-1916 гг. вышло большое количество учебных пособий, которые отражали смешение вопросов о трактовке понятия функции и способов ее задания, т.е. содержали рассмотрение способов задания функции (аналитического, графического, табличного) в контексте понятия функции.
Третий этап развития русской школы начался в 20-е гг. двадцатого столетия. Анализ методической литературы советского периода показал, что введение понятия функции в школьный курс математики сопровождалось бурными дискуссиями, и позволил нам выделить четыре основных проблемы, вокруг которых существовали расхождения во мнениях методистов, а именно: 1) цель и значение изучения понятия функции учащимися; 2) подходы к определению функции; 3) вопрос функциональной пропедевтики; 4) место и объем функционального материала в курсе школьной математики начальной школы.
Первые послереволюционные программы, составленные в 1918-1921гг., отражали стремление их авторов к коренному преобразованию школьного курса математики начальной школы. При их разработке были учтены основные достижения передовой педагогической мысли того времени: курс математики строился на основе понятия функции. Авторы программ считали, что все включенное в программу "должно быть проработано основательно, главным образом, в направлении развития функционального мышления, при этом идейной и практической стороне должно отдать предпочтение перед формальной" [11, с.380].
Анализ программ позволил выделить их положительные и отрицательные стороны. Главное достоинство, на наш взгляд, - это разделение вопросов о трактовке понятия функциональной зависимости и способах задания функции. Общим недостатком была перегруженность их в той' или иной степени учебным материалом, который, к тому же, был распределен по годам обучения без учета возрастных особенностей учащихся. Как следствие, на практике не удалось в полном объеме выполнить предъявленные данными программами требования.
Не исправили положение программы на основе "комплексного" метода, суть которого состояла в том, что взамен систематического изложения школьного курса математики начальной школы, опирающегося на внутреннюю логику предмета, преподавание строилось в соответствии с последовательностью, содержанием и основными идеями комплексных схем. Известный советский методист Н.Н. Никитин указывал на утилитарность комплексных программ и методических указаний к ним, приведшую к снижению уровня математической подготовки учащихся. "Учащиеся получали поверхностное, случайное знакомство со многими вопросами из математики, но по-настоящему прочно и сознательно знать ничего не могли" [37, с.115].
Итак, данный этап, полностью обусловленный политической и экономической нестабильной ситуацией в России 20-х гг., характеризуется разногласием в действиях методистов, их стремлением к отказу от достижений в области отечественной методики преподавания математики. Разногласия методистов в решении проблем, связанных с определением цели и значения изучения функции учащимися, места и объема функционального материала в курсе школьной математики, а также отсутствие единого мнения по вопросу функциональной пропедевтики привели к ухудшению качества знаний учащихся.
Кризисная ситуация в области преподавания математики вызвала необходимость пересмотра и проверки методов школьной работы.
Четвертый этап обусловлен переводом экономики РСФСР на плановую основу.
В 1931-34 годы была предпринята попытка перехода школьного образования на позиции систематического и прочного усвоения наук. В данный период срок обучения в школе был увеличен до десяти лет, основной формой работы в школе был утвержден урок, была восстановлена роль учебника как основного руководства для ученика, с систематическим изложением основ наук и полным охватом содержания программы по предмету.
Формирование представления о функции, прежде всего как об аналитическом выражении, ученые расценивают как проявление формализма в преподавании, для которого "характерно неправомерное доминирование в сознании и памяти учащихся привычного внешнего (словесного, символического или образного) выражения математического факта над содержанием этого факта" [21, с.46].
Они считали, что в начальной школе понятие функции необходимо изучать на основе понятия соответствия. Для нашего исследования важным является подход А.Я. Хинчина к разработке системы упражнений, способствующих усвоению понятия функции. Он указывал, что традиционные примеры, рассматриваемые непосредственно после введения понятия функции, способны разрушить положительный эффект определения и привить учащимся мысль, что формальное определение само по себе, а в действительности функция есть просто формула. По его мнению, уже среди первых примеров функциональной зависимости наряду с традиционными алгебраическими и геометрическими соотношениями необходимо рассматривать и функции, заданные без использования формулы.
Данный период характеризуется недостаточностью времени на изучение функций, непродуманностью систем упражнений, непониманием учащимися истинной сущности понятия функции, низким уровнем функциональных и графических навыков выпускников школ.
Таким образом, вновь возникла потребность в реформировании преподавания математики в начальной школе. Перестройка всей школьной математики на основе теоретико-множественного подхода ознаменовала пятый этап развития идеи функциональной зависимости. Идея, теоретико-множественного подхода была предпринята группой французских ученых, объединившихся под псевдонимом Николя Бурбаки. В г. Роймоне (Франция, 1959 г.) состоялось международное совещание, на котором было провозглашено свержение всех обычных курсов. В центре внимания оказались структуры и объединения всей школьной математики на базе теории множеств [25, с.174].
Важную роль в развитии идей реформы сыграли статьи В.Л. Гончарова, в которых автор указывал на важность ранней и длительной функциональной пропедевтики, предлагал использовать упражнения, заключающиеся в выполнении ряда заранее указанных числовых подстановок в одном и том же заданном буквенном выражении. Эти упражнения, наряду с совершенствованием вычислительных навыков, могли бы служить и идеям функциональной пропедевтики. Ученый особое внимание отводил построению графика функции, заданной использованным для вычислений буквенным выражением. Особую целесообразность он видел в том, "чтобы две капитальной важности и высокой трудоемкости проблемы — сообщения учащимся прочных навыков арифметических вычислений и пропедевтическое ознакомление их с идеей функции могли быть разрешаемы совместно" [22, с.153].
Таким образом, стабилизация программ и учебников создала почву для возникновения положительных сдвигов в качестве функциональных знаний учащихся. В конце шестидесятых - начале семидесятых, наряду с отрицательными отзывами, в печати стали появляться и такие, в которых отмечалось определенное улучшение знаний школьников о функциях и графиках. Однако общий уровень математического развития учащихся в целом оставался недостаточным. В школьном курсе математики по-прежнему неоправданно много времени отводится формальной подготовке и не уделяется должного внимания формированию представлений младших школьников о функциональной зависимости.
Виды упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников мы рассмотрим в следующем параграфе.
1.3
Виды упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников
Для организации учебной деятельности учащихся начальных классов, направленной на эффективную подготовку к формированию представлений о функциональной зависимости должны выполняться следующие дидактические условия: наличие в курсе математики идей, непосредственно связанных с функциональными представлениями, таких как идея изменения, соответствия, закономерности и зависимости; наличие в содержании курса математики понятий, необходимых для осознанного усвоения понятия функции; создание проблемных ситуаций в процессе усвоения программного содержания; систематическое использование различных моделей (предметной, вербальной, символической, схематической и графической); использование учебных заданий, в основу которых положены приемы выбора, сравнения, преобразования и конструирования; организация целенаправленного наблюдения, сравнения, анализа и обобщения в процессе выполнения учебных заданий [4, с.110].
Для организации деятельности учащихся, направленной на формирование функциональных представлений и понятий, необходимых для восприятия и усвоения понятия «функция», целесообразно использовать учебные задания следующих видов: задания на тождественные преобразования числовых выражений (равенств) на основе смысла арифметического действия; на соотнесение предметной модели с числовым выражением (равенством); на соотнесение предметной, графической и символической моделей; на выявление закономерности; на установление соответствия между символическими моделями; на конструирование графической модели по заданной графической модели; на конструирование символической модели по заданной вербальной модели; на выбор символической модели, соответствующей вербальной модели; на конструирование числовых равенств по заданным условиям; на установление соответствия между символической и графической моделью; на выбор графической модели соответствующей символической модели; на преобразование на плоскости; на конструирование графической модели, соответствующей символической модели и т.д. [5, с.23].
Учебные задания, способствующие формированию функциональных представлений и понятий, необходимых для осознанного усвоения понятия функции, должны характеризоваться:
1) вариативностью;
2) неоднозначностью решений;
3) нацеленностью на формирование приемов умственной деятельности (таких, как анализ и синтез, сравнение, аналогия, классификация и обобщение);
4) отображением разнообразных закономерностей и зависимостей;
5) включенностью их в содержательную линию курса математики начальных классов [17, с.81].
На основе функциональных представлений разработаны учебные задания, направленные на их формирование:
1. Задания на формирование представлений об изменении и зависимости: на изменение результата арифметического действия в зависимости от изменения его компонентов; на использование основного свойства дроби; на классификацию числовых выражений (равенств) на основе их результата арифметического действия; тождественные преобразования числовых выражений (равенств) на основе смысла арифметического действия; на преобразование числовых выражений; на преобразование дробных выражений; на конструирование символической модели по заданной вербальной модели и др.).
Например, «Чем похожи все пары выражений? Найди их значения:
а) 89 + 47 б) 57+29 в) 76+57
90 + 47 57+30 76+60
Сравни равенства в каждой паре и сделай вывод».
2. Задания на формирование представления о закономерности, как правила, по которому записаны ряды чисел: на выявление закономерности.
Например, «Найди правила, по которым составлены ряды чисел:
а) 0,5; 0,05; 0,005; 0,0005; …;
б) 0,2; 0,4; 0,6; 0,8; …;
в) 0,12; 2,14; 4,16; 6,18; ….
Запиши в каждом ряду еще три числа по тому же правилу».
3. Задания на формирование представления о соответствии: на соотнесение предметной, графической и символической моделей; на установление соответствия между символическими моделями.
Например, «Соедини с числом 5 те выражения, значения которых делятся на 5, если а делится на 5».
Эти учебные задания формулируются в основном на числовом материале, причем они усложняются и варьируются как по форме, так и по содержанию.
Решение задач на прямую и обратную пропорциональные зависимости посвящен решению текстовых задач на прямую и обратную пропорциональные зависимости арифметическим способом. Среди таких задач выделяются задачи, в которых числовые данные находятся в некотором отношении, что предполагает ещё один способ решения, представляющий интерес с точки зрения функциональной пропедевтики [36, с.105].
Кроме того, придать функциональный характер текстовым задачам можно с помощью дополнительных вопросов, направленных на изменение данных задачи, условия, вопроса, на соотнесение условия с различными выражениями и равенствами. Эти приемы помогают учащимся представить величины, рассматриваемые в задаче в движении, изменении, что позволяет формировать у учащихся функциональный стиль мышления.
На программном содержании курса математики начальных классов используются также учебные задания следующих видов:
1) задания на соотнесение предметной модели с числовым выражением (равенством);
2) задания на установление соответствия между символическими моделями;
3) задания на конструирование графической модели по заданной графической модели;
4) задания на конструирование символической модели по заданной вербальной модели;
5) задания на выбор символической модели, соответствующей вербальной модели;
6) задания на конструирование числовых равенств по заданным условиям;
7) задания на установление соответствия между символической и графической моделью;
8) задания на выбор графической модели, соответствующей символической модели;
9) задания на преобразование на плоскости;
10) задания на конструирование графической модели, соответствующей символической модели и т.д. [20, с.110].
Приведем примеры заданий:
1. Задание на конструирование числовых равенств по заданным условиям:
Выбери два отношения, из которых можно составить верное равенство. Запиши это равенство:
1,5 : 2; 3 : 6; 4,5 : 8; 6 : 8; 15 : 10.
2. Задание на конструирование графической модели, соответствующей символической модели:
Проверь, будут ли величины х и у прямо пропорциональными при данных значениях:
| х |
1 |
4 |
16 |
64 |
256 |
| у |
0,6 |
2,4 |
9,6 |
38,4 |
153,6 |
Если возникнут трудности при выполнении задания, то:
представь данную таблицу в таком виде:
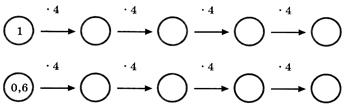
и найди отношения соответствующих значений величин х и у.
3. Задание на преобразование на плоскости:
Впиши пропущенные слова и числа, чтобы получились верные высказывания:
1) точка А (3; 4) при перемещении вправо на 2 единичных отрезка перешла в точку В (…;…);
2) точка L (5; -2) при перемещении______________на___единичных отрезков перешла в точку M (5; 2);
3) точка Х (1; 1) при перемещении вверх на 3 и вправо на 6 единичных отрезков перешла в точку У (…;…);
4) точка V (2; 3) при перемещении__________на___и___________ на___ единичных отрезков перешла в точку W (7; -2).
4. Задание на конструирование графической модели, соответствующей символической модели:
а) Выбери единичный отрезок и построй точки в координатной плоскости:
А (0,6; 0), В (0; 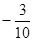 ), С (0,1; 0,7), D ), С (0,1; 0,7), D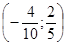 , E , E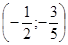 , К , К 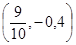 . .
б) Выбери единичный отрезок и построй точки в координатной плоскости:
А(600; 0), B(0; -300), C(100; 700), E(-500; -600), K(900; -400).
Все учебные задания, обладают следующими характеристиками: вариативностью; неоднозначностью решений; нацеленностью на формирование приемов умственной деятельности (таких, как анализ и синтез, сравнение, аналогия, классификация и обобщение); отображением разнообразных закономерностей и зависимостей; включенностью их в содержательную линию курса математики начальных классов [10, с.95].
Таким образом, рассмотрев теоретические основы формирования представлений о функциональной зависимости у младших школьников, мы пришли к выводу, что функциональная зависимость является одной из тех математических идей, которые способны объединить в единое целое все разделы математики, включенные в школьный курс. Функциональная зависимость отражает практическую направленность курса математики, взаимосвязь величин в естественнонаучных дисциплинах, а также формирует функциональное мышление школьников. Исходя из опыта обучения, известно, что понятие функции является абстрактным и довольно сложным для восприятия учащимися. Поэтому в процессе реализации данной линии необходимо усилить наглядность изучаемых объектов и понятий в рамках отведенного времени, предоставить учащимся возможность увидеть зависимость не только в виде статичной модели, но и в динамике, дать возможность учащимся непосредственно задавать, изменять и изучать функции при помощи интерактивных моделей, расширить систему задач при помощи упражнений, содержащих анимацию и элементы управления и т.д. Такому «живому» изучению функциональной зависимости может способствовать применение комплекса упражнений, направленных на формирование представлений о функциональной зависимости.
Следующая глава будет посвящена экспериментальной работе по формированию представлений младших школьников о функциональной зависимости.
Глава 2. Опытно-экспериментальная работа по формированию представлений о функциональной зависимости у младших школьников с применением комплекса упражнений
2.1 Диагностика уровней сформированности представлений младших школьников о функциональной зависимости
Для формирования представлений у младших школьников о функциональной зависимости на базе МОУ СОШ №31 города Ишима был проведен эксперимент.
В эксперименте приняли участие учащиеся 3 «А» (экспериментальная группа) и 3 «Б» (контрольная группа) классов в количестве по 20 человек в каждом классе. Список детей, участвующих в исследовании приведен в приложении 1.
Эксперимент состоял из трех этапов:
1 этап – констатирующий этап - диагностика уровня сформированности представлений о функциональной зависимости у младших школьников.
2 этап – формирующий этап - разработан и реализован комплекс упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников.
3 этап – контрольный этап - проведен анализ эффективности занятий с применением комплекса упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников.
Для выявления уровня сформированности представлений о функциональной зависимости у младших школьников были выделены следующие функциональные умения:
1) строить график функции;
2) записывать координаты точек;
3) находить наибольшее и наименьшее значения функции на заданном промежутке;
4) оперировать функциональной символикой.
На основе выделенных умений, а также для аналитической обработки результатов исследования и получения количественных показателей были выделены три уровня сформированности представлений о функциональной зависимости у младших школьников: низкий, средний и высокий.
С целью определения уровня сформированности представлений о функциональной зависимости у младших школьников в ходе констатирующего эксперимента организовывались беседы с учащимися 3-х классов, проводились контрольные работы, по результатам выполнения которых выявлялись трудности, возникающие у учащихся при усвоении понятия функции, функциональной зависимости.
Чтобы оценить способность учащихся применять функциональные умения для решения практических задач им были предложены ситуационные задачи. В силу своей межпредметности, интегративности ситуационные задачи способствуют систематизации предметных знаний на деятельностной практико-ориентированной основе, когда ученики, осваивая универсальные способы деятельности, решают личностно-значимые проблемы с использованием предметных знаний. Следует отметить, что в процессе обучения математике учащиеся ни экспериментального, ни контрольного классов с такими задачами не встречались.
Приведем пример одной из ситуационных задач, которые предлагались учащимся:
Задача. «Эти простые – непростые зависимости»
Каждый слышал поговорку: «Как аукнется, так и откликнется». А ты замечал на себе проявление такой закономерности?
Текст 1. Маша и Миша решили посадить одновременно цветы, чтобы подарить их маме к 8 марта. В течение 12 недель Маша поливала цветок регулярно, а Миша иногда забывал. Высота цветка Маши в конце каждой недели представлена в таблице 1:
| Неделя, t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Высота
цветка, h (см)
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
Текст 2. Существуют различные шкалы для измерения температуры. Для перевода температуры, измеренной в градусах Цельсия, в градусы Фаренгейта пользуются формулой 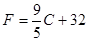 , где С – число градусов по шкале Цельсия, а F – число градусов по шкале Фаренгейта. Для каждого значения температуры по Цельсию с помощью этой формулы можно найти соответствующее значение температуры по шкале Фаренгейта. , где С – число градусов по шкале Цельсия, а F – число градусов по шкале Фаренгейта. Для каждого значения температуры по Цельсию с помощью этой формулы можно найти соответствующее значение температуры по шкале Фаренгейта.
Задания.
1. Пользуясь таблицей роста цветка Маши, составь таблицу роста цветка Миши, учитывая, что его цветок рос в два раза медленнее (из-за забывчивости Миши).
2. Найди высоту цветка Миши через 3,5 недели. Опиши процесс нахождения ответа на вопрос.
3. Составь таблицу перевода значений температуры из градусов по Цельсию в градусы по Фаренгейту (для значений от 0° С до 30° С).
4. Выяви зависимости, описанные в тексте 1 и тексте 2. Сравни их.
5. Предложи жизненные ситуации, в которых проявляются закономерности, выявленные тобой из анализа текста 1 и 2.
Проанализировав результаты работ учащихся по четырем умениям, можно прийти к следующим выводам:
- учащиеся как 3 «А», так и 3 «Б» классов понимают представленную информацию, предлагают способы решения проблемы, но при обосновании способа решения учащиеся 3 «А» класса в меньшей степени оперируют функциональными представлениями;
- учащиеся 3 «А класса при выполнении задания, где нужно было привести примеры зависимостей, аналогичных тем, что были предложены в задаче, приводят примеры таких зависимостей, т.е. зависимостей, которые являются функциональными, в то время как учащиеся 3 «Б» класса предлагают зависимости, исходя из своего представления о них.
Таким образом, большее количество учащихся 3 «А» класса слабо оперирует функциональными представлениями и не способно применить сформированные функциональные умения для решения новых практических задач.
Данные констатирующего этапа эксперимента приведены в таблице 2.
Таблица 2
Показатели уровня сформированности представлений о функциональной зависимости у младших школьников по критериям на констатирующем этапе эксперимента
| Класс |
Функциональные умения младших школьников |
| строить график функции |
записывать координаты точек |
находить наибольшее и наименьшее значения функции на заданном промежутке |
оперировать функциональной символикой |
| Низкий уровень |
Средний уровень |
Высокий уровень |
Низкий уровень |
Средний уровень |
Высокий уровень |
Низкий уровень |
Средний уровень |
Высокий уровень |
Низкий уровень |
Средний уровень |
Высокий уровень |
| 3 «А» класс |
5 |
14 |
1 |
4 |
15 |
1 |
4 |
14 |
2 |
3 |
16 |
1 |
| 3 «Б» класс |
1 |
16 |
3 |
- |
13 |
7 |
1 |
14 |
5 |
2 |
15 |
3 |
В результате проведенной работы на констатирующем этапе эксперимента было установлено, что 30% всех испытуемых имеют низкий уровень сформированности представлений о функциональной зависимости, исходя из четырех критериев, определенных в начале эксперимента, 57 % испытуемых показали средний уровень и лишь 13% младших школьников имеют высокий уровень сформированности представлений о функциональной зависимости.
Анализ полученных результатов позволил сделать вывод о том, что большая часть младших школьников имеет средний и низкий уровень сформированности представлений о функциональной зависимости и нуждается в коррекции. Следовательно, результаты констатирующего этапа исследования требуют проведения формирующего этапа эксперимента в соответствии с предложенной гипотезой.
2.2 Реализация комплекса упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников
С целью формирования у младших школьников представлений о функциональной зависимости нами был проведен формирующий этап эксперимента, в котором приняли участие только учащиеся экспериментального 3 «А» класса. Для этого нами применялся комплекс подобранных для этой цели упражнений, направленных на формирование функциональной зависимости у младших школьников. Изучение проводилось по теме школьного курса математики «Зависимость между результатами и компонентами арифметических действий». По теме проводилось пробное и основное исследование.
Зависимость между элементами арифметических действий изучалась каждым из испытуемых в индивидуальном порядке под руководством экспериментатора один раз, затем второй, третий, — так до полного овладения ею. В конце исследования-обучения давалась в индивидуальном порядке контрольная работа.
Изучение зависимости между элементами геометрических фигур проводилось в течение нескольких уроков. Сначала учащиеся знакомились с простейшими случаями зависимости между площадью и стороной прямоугольника при постоянной величине смежной стороны. Затем — с зависимостью между сторонами и площадью квадрата. И, наконец, со школьниками велись занятия-исследования по обучению их пониманию и усвоению зависимости между основанием, высотой и площадью прямоугольника, параллелограмма и треугольника при постоянной величине суммы их основания и высоты.
Все занятия проводились в индивидуальном порядке. В конце исследования-обучения в индивидуальном же порядке давалась контрольная работа.
По теме «Зависимость между компонентами и результатами действий» работа проводилась следующим образом.
Группа изучала материал в таком порядке изменение суммы, затем — изменение произведения, далее — изменение разности и, наконец, — изменение частного.
Затем группа изучала материал в том же порядке, но в одновременном противопоставлении изменению компонентов изменения результатов действий.
И, наконец, группа изучала материал в следующем порядке: изменение суммы, затем — изменение разности, далее — изменение произведения и, наконец, — изменение частного.
Для изучения зависимости между изменением площади и изменением входящих и ее выражение компонентов были созданы группы, работавшие:
Первая группа — с графиками.
Вторая группа — с графиками + наглядное изображение образа меняющейся фигуры в тетради
Третья группа — с диаграммами.
Четвертая группа — с наглядным изображением образа меняющейся фигуры в тетради
В изучении зависимости между элементами действии ученик пользуется конкретным примером. Он постепенно переходит от использования данного единичного примера, как необходимого в выражении зависимости, к использованию его, как возможного для выражения разбираемой зависимости.
В активной деятельности с вариативным использованием примеров ученик в процессе обучения доходит до понимания и усвоения обобщенного характера изменения зависимых величин, от «живого созерцания» он поднимается к «абстрактному мышлению» и затем конкретизирует обобщенные знания в практическом применении. Все это связано с совершенствованием анализа и синтеза в совместной деятельности первой и второй сигнальных систем при ведущей роли второй, словесной системы мозговой коры.
При решении задач в первое время ученики не осмысливали их на базе заключенной в них функциональной зависимости, за внешним оформлением не вскрывали сущности изученной уже в принципе ими зависимости. Обобщающая и конкретизирующая деятельность реализовалась лишь применительно к заданиям — примерам. Она не переносилась на решение задач. Развитие умения переосмысливать решение примеров на основе функциональной зависимости в дальнейшей работе ученика, в связи с совершенствованием избирательной иррадиации и развитием подвижности мозговых процессов, переносилось и на решение задач.
В исследовании обнаружилось смешение школьниками разностных и кратных изменений, происходящих в зависимых величинах. Это обусловливалось там, что на предыдущих этапах обучения изучение этих изменений проводилось без надлежащего использования сравнения, особенно сравнения в виде противопоставления.
При изучении обратной зависимости изменения ученики обычно на первых занятиях обратную зависимость подменяли прямою, а количественное изменение устанавливали подбором. Выработанный стереотип понимания отношения между величинами прямого изменения переносился на выполнение задания с обратным изменением. В процессе дальнейшей систематической работы понимание обратной зависимости учениками совершалось от частичного привнесения обратного изменения в прямую зависимость к полной замене прямой зависимости обратной.
Формирование понимания зависимости происходило только в непосредственной деятельности с заданием. Часто первичное восприятие задания приводило к ошибочному его выполнению. Дальнейшая работа над заданием раскрывала перед учеником существенные связи, сначала им незамеченные.
Понимание зависимости между изменением одного компонента и изменением результата действия совершается сначала в динамике качественного изменения. Количественная отдифференцированность изменения происходит позднее, причем в изменении разности и частного она носит более сложный характер и требует для понимания больше усилий, чем в изменении суммы и произведения. Это первая ступень в понимании зависимости между компонентами и результатами действия.
Затем школьники поднимаются к пониманию и усвоению зависимости между изменением обоих компонентов и изменением результата действия. На этой второй ступени в понимании зависимости школьники проходят несколько этапов.
На первом этапе работы все задание по установлению зависимости между тремя элементами выполнялось школьниками обычно неверно. Они не могли еще осмыслить полностью одновременное изменение трех величин.
Понимание зависимости начиналось с выяснения качественного характера изменения величин.
Понимание изменений в сложении и умножении наступало раньше, чем в вычитании и делении.
Обратная зависимость на этом этапе работы не понималась.
На втором этапе этой ступени в отличие от первого этапа заданные изменения понимались учеником как проявление функциональной зависимости. Выполнялись все предложенные изменения не как арифметические действия над заданными числами, а как результативные изменения величин, зависимых от заданных изменений других величин.
Однако на этом этапе работы обнаружился ряд трудностей, специфичных для понимания сложного характера изменения элементов вычитания и деления, в силу чего качественное и количественное изменения элементов этих действий нередко определялось неверно.
На следующем этапе наступало понимание вариативности изменения между качественным характером поведения зависимых величин и их количественным выражением. Для действий сложения и вычитания расхождений не обнаруживалось.
При изучении вариативных изменений в действиях умножении и делении характер изменения иногда отрывался учеником от количественного выражения, и, обычно уменьшение выполнялось вычитанием, а увеличение — сложением.
В действиях вычитания и деления обнаружился отрицательный перенос изменения последнего компонента на изменение результата действия. Старые связи, отношения, образовавшие стереотипную систему изменений в сложении и умножении, тормозили понимание новых отношений и формирование новых связей.
Наконец, на третьей ступени школьники начинали понимать обратный характер зависимости между элементами арифметических действий. Понимание обратной зависимости для каждого действия шло через использование прямого характера изменения. Понимание обратной зависимости для всех арифметических действий при решении примеров и задач происходила медленнее, чем понимание прямой зависимости.
Овладение зависимостью между компонентами и результатами действий выразилось в развитии у школьников тесной связи абстрагирующей и конкретизирующей мыслительной работы. Сформировавшиеся обобщенные, понятийные знания о зависимости между элементами действий школьники начинали умело применять к решению новых примеров и задач, к самостоятельному составлению примеров и задач на заданную зависимость. Школьники начинали понимать рациональное значение применения понятийного знания зависимости к решению конкретных арифметических задач.
При изучении зависимости между элементами геометрических фигур ученик стремился представить себе наглядный образ изменяющейся фигуры. Но ввиду ограниченности геометрических знаний образ фигуры оказывается у него неподвижным, статическим, лишенным изменений.
На начальных этапах изучения зависимости между величинами геометрической фигуры понимание ее происходило не через соотношение элементов конкретного, разбираемого образа. Сначала зависимость в ее понятийном содержании понималась через известный и более простой математический материал, через активизацию знаний и пришлого опыта. Затем полученное понятийное знание зависимости соответственно выражалось в наглядных образах.
Привлечение наглядного образа играет двоякую роль: оно может и помогать, облегчать установление заключенной в задаче зависимости, а может мешать, заслонять ее. Отрицательная роль наглядных образов проявляется тогда, когда они говорят ученику лишь об отдельных частных случаях разбираемой зависимости.
Для проверки эффективности реализованного комплекса упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников, нами была проведена повторная диагностика уровней сформированности представлений о функциональной зависимости школьников экспериментальной и контрольной групп.
Методика контрольного обследования совпадала с методикой констатирующего обследования уровня сформированности представлений о функциональной зависимости. Данные контрольного этапа эксперимента по проведенной диагностике в экспериментальной и контрольной группах испытуемых приведены в таблице 3. Результаты анализировались с привлечением данных констатирующего обследования уровня сформированности представлений о функциональной зависимости.
Таблица 3
Показатели уровня сформированности представлений о функциональной зависимости в экспериментальной группе на контрольном этапе эксперимента
| Уровень сформированности представлений о функциональной зависимости |
Количествонаблюдений |
% |
| Низкий |
0 |
0 |
| Средний |
7 |
70 |
| Высокий |
3 |
30 |
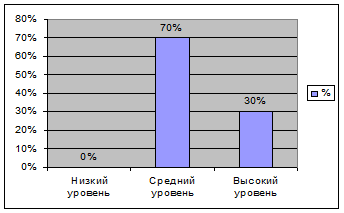
Рис.1 Уровень сформированности представлений о функциональной зависимости в экспериментальной группе на контрольном этапе
Для наглядности показатели уровня сформированности представлений о функциональной зависимости в экспериментальной группе на контрольном этапе эксперимента представлены на рисунке 1.
Таблица 4
Показатели уровня сформированности представлений о функциональной зависимости в контрольной группе на контрольном этапе эксперимента
| Уровень сформированности представлений о функциональной зависимости |
Количествонаблюдений |
% |
| Низкий |
2 |
20 |
| Средний |
5 |
50 |
| Высокий |
3 |
30 |
 Для наглядности показатели уровня сформированности представлений о функциональной зависимости в контрольной группе на контрольном этапе эксперимента представлены на рисунке 2. Для наглядности показатели уровня сформированности представлений о функциональной зависимости в контрольной группе на контрольном этапе эксперимента представлены на рисунке 2.
Рис.2 Уровень сформированности представлений о функциональной зависимости в контрольной группе на контрольном этапе
Оценка динамики изменения уровня сформированности представлений о функциональной зависимости в экспериментальной группе на констатирующем и контрольном этапах эксперимента представлена в таблице 5.
Таблица 5
Показатели уровня сформированности представлений о функциональной зависимости в экспериментальной группе на констатирующем и контрольном этапах эксперимента
| Уровень сформированности представлений о функциональной зависимости |
Констатирующий этап (%) |
Контрольный этап(%) |
| Низкий |
20 |
0 |
| Средний |
60 |
70 |
| Высокий |
20 |
30 |
Для наглядности представим сравнительный анализ уровня сформированности представлений о функциональной зависимости в экспериментальной группе на констатирующем и контрольном этапе на рисунке 3.
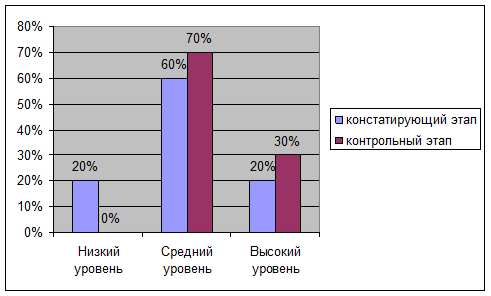
Рис.3 Сравнительный анализ уровня сформированности представлений о функциональной зависимости в экспериментальной группе на констатирующем и контрольном этапе
Сравнение данных констатирующего этапа с данными, полученными на контрольном этапе показывает, что количество школьников с низким уровнем сформированности представлений о функциональной зависимости уменьшилось до 0, на 10 % увеличилось количество школьников, имевших средний уровень сформированности представлений о функциональной зависимости. За счет уменьшения количества низкого уровня сформированности представлений о функциональной зависимости на 10% увеличилось количество школьников, показавших высокий уровень сформированности представлений о функциональной зависимости. В целом, это доказывает, что содержание и приемы формирующего этапа эксперимента были выбраны правильно и оказались эффективными для повышения уровня сформированности представлений о функциональной зависимости у младших школьников.
Незначительные изменения уровня сформированности представлений о функциональной зависимости контрольной группы, выявленные на контрольном этапе: уменьшение на 10% школьников с высоким и увеличение на 10% с низким уровнем сформированности представлений о функциональной зависимости, средний уровень сформированности представлений о функциональной зависимости без изменений подтверждает предположения, что без применения упражнений достижение существенного изменения сформированности представлений о функциональной зависимости у младших школьников весьма затруднительно.
Сравнительный анализ уровня сформированности представлений о функциональной зависимости экспериментальной и контрольной групп на контрольном этапе эксперимента представлен в таблице 6.
Таблица 6
Показатели уровня сформированности представлений о функциональной зависимости экспериментальной и контрольной групп на контрольном этапе эксперимента
| Уровень сформированности представлений о функциональной зависимости |
Экспериментальная группа (%) |
Контрольнаягруппа(%) |
| Низкий |
0 |
20 |
| Средний |
70 |
50 |
| Высокий |
30 |
30 |
Таким образом, контрольный этап эксперимента позволил прийти к выводу о том, что для формирования представлений о функциональной зависимости у младших школьников необходимо разрабатывать и применять упражнения, направленные на формирование представлений о функциональной зависимости.
Заключение
Одним из видов объективно существующих связей является математическая функциональная зависимость.
Понятие функциональной зависимости является одним из основных понятий всей математики, в том числе и элементарной. Если одна величина стоит в зависимости от другой, то при изменении последней (независимого переменного), первая (т. е. функция) будет изменяться по известному закону; таким образом, каждое частное значение независимого переменного вполне определяет соответствующее значение функции.
Школьные программы должны быть построены так, чтобы идеи переменной величины и функциональной зависимости, являющиеся прямым математическим выражением основных черт диалектического миропонимания, как можно ранее усваивались учащимися и как можно ранее становились основным стержнем всего школьного курса математики.
В нашем исследовании мы рассмотрели понятие «функциональная зависимость» в методической литературе, выявили педагогические идеи преподавания функциональной зависимости в начальной школе, изучили виды упражнений, направленных на формирование представлений о функциональной зависимости у младших школьников.
Для исследования и проверки эффективности комплекса подобранных нами упражнений для формирования представлений о функциональной зависимости нами было проведена опытно-экспериментальная работа. На констатирующем этапе исследования нами был определен уровень сформированности представлений о функциональной зависимости у младших школьников. Было установлено, что большинство учащихся 3 классов имеют низкий уровень сформированности представлений о функциональной зависимости. Для формирования представлений нами был проведен формирующий этап эксперимента, на котором нами были использованы упражнения, направленные на формирование представлений о функциональной зависимости. Контрольный этап экспериментального исследования показал, что в результате формирующего этапа уровень сформированности представлений о функциональной зависимости у младших школьников экспериментальной группы значительно изменился.
Таким образом, задачи, поставленные в начале работы, нами были решены, цель исследования достигнута, гипотеза подтверждена.
Библиография
1. Аматова, Г.И. Математика [Текст]/Г.И. Аматова, М.А. Аматов. -М.: Московский психолого-социальный институт, 1999. – 337 с.
2. Аммосова, Н.В. Понятие функциональной зависимости в начальной школе [Текст] / Аммосова Н.В. // Начальная школа. - 2000. - №5.- С.109-114.
3. Байрамукова, П.У. Внеклассная работа по математике [Текст] / П.У. Байрамукова. – М.: Издат-школа «Райл», 1997. – С.214.
4. Бантова, М.А. Методика преподавания математики в начальных классах [Текст] /М.А. Бантова, Г.В. Бельтюкова. – М.: Просвещение, 1984. – 335 с.
5. Боцманова, М.Э. Психологические вопросы применения графических схем учащимися начальной школы [Текст]/М.Э. Боцманова// Вопросы психологии. – 1960. – №5.
6. Виленкин, Н.Я. Задачник практикумом по математике [Текст] / Н.Я.Виленкин, Н.Н.Лаврова, В.Б.Рождественская, Л.П. Стойлова. – М.: Просвещение, 1985. – С.142.
7. Виленкин, Н.Я. Математика [Текст]/Н.Я. Виленкин, Л.М. Пышкало, В.Б. Рождественская, Л.И. Стойлова. – М.: Просвещение, 1977. – С.220.
8. Зак, А.З. 600 игровых задач для развития логического мышления детей [Текст] /А.З. Зак. - Ярославль: Академия развития, 1998. – 175 с.
9. Истомина, Н.Б. Активизация учащихся на уроках математики в начальных классах: Пособие для учителя [Текст]/Н.Б. Истомина.– М.: Просвещение, 1985. –– 64 с.
10. Истомина, Н.Б. и др. Практикум по методике преподавания математики в начальных классах [Текст]/ Н.Б. Истомина, Л.Г. Латохина, Г.Г. Шмырева. – М.: Просвещение, 1986. – 176 с.
11. Истомина, Н.Б. Методика обучения математике в начальных классах [Текст] /Н.Б. Истомина. - М.: ACADEMA, 2000. – 453 с.
12. Истомина, Н.Б. Методика обучения математике в начальных классах [Текст] /Н.Б. Истомина. – М.: Издательский центр «Академия», 1998. – 288 с.
13. Котов, А.Я. Вечера занимательной математики [Текст]/А.Я.Котов. – М.: Просвещение, 1967. – С.117.
14. Крутецкий, В.А. Психология математических способностей школьников [Текст] /В.А. Крутецкий. – М.: Просвещение,1968. – 432 с.
15. Кульневич, С.В. Нетрадиционные уроки в начальной школе [Текст] / С.В. Кульневич, Т.П. Лакоценина. — Ростов н/Д: ТЦ «Учитель», 2002. – 375 с.
16. Марушенко, Л.Ю. Арифметическая задача как средство формирования первых функциональных представлений у учащихся [Текст] / Л.Ю. Марушенко // Новые технологии в обучении физике, математике и информатике: материалы региональной научно-практической конференции, посвященной памяти чл.-корр. РАЕН, проф., доктора педагогических наук А.А. Пинского. – Благовещенск: Издательство БГПУ, 2007. – С. 107 - 115.
17. Марушенко, Л.Ю. К вопросу об изучении функций в школе [Текст]/Л.Ю. Марушенко//Новые технологии в обучении физике, математике и информатике: материалы региональной научно-практической конференции, посвященной памяти чл.-корр. РАЕН, проф., доктора педагогических наук А.А. Пинского. – Благовещенск: Издательство БГПУ, 2005. - С. 81-83.
18. Марушенко, Л.Ю. К проблеме изучения понятия функции в школьном курсе математики [Текст] /Л.Ю. Марушенко// Актуальные вопросы методики преподавания математики и информатики в свете модернизации Российского образования: сборник научных трудов Всероссийской научно-практической конференции, 17 апреля 2006 г. – Биробиджан: Изд-во ДВГСГА, 2006. – 263 с.
19. Марушенко, Л.Ю. Об оценке качества усвоения понятия функции учащимися старших классов [Текст] / Л.Ю. Марушенко // Новые технологии в обучении физике, математике и информатике: материалы региональной научно-практической конференции, посвященной памяти чл.-корр. РАЕН, проф., доктора педагогических наук А.А. Пинского. – Благовещенск: Издательство БГПУ, 2008. - С. 121-125.
20. Марушенко, Л.Ю. Пропедевтика функциональной зависимости в курсе математики средней школы [Текст] / Л.Ю. Марушенко// Новые технологии в обучении физике, математике и информатике: материалы региональной научно-практической конференции, посвященной памяти чл.-корр. РАЕН, проф., доктора педагогических наук А.А. Пинского. – Благовещенск: Издательство БГПУ, 2006. - С. 110-111.
21. Марушенко, Л.Ю. Функциональный подход к решению текстовых задач на прямо пропорциональную зависимость [Текст]/Л.Ю. Марушенко// Начальная школа. - 2007. - №7. – С. 44-51.
22. Методика начального обучения математике / под ред. Л.Н. Скаткина. – М.: Просвещение, 1972. – 320 с.
23. Методика начального обучения математике. Под общей редакцией А.А. Столяра и В.Л. Дрозда. Минск: Вышэйшая школа, 1988. – 234 с.
24. Методика начального обучения математике: Учеб. пособие для пед. ин-тов / В.Л. Дрозд, А.Т. Касатонова, Л.А. Латотин и др.; Под общ. ред. А.А. Столяра, В.Л. Дрозда. – Мн.: Выш. шк., 1988. – 254 с.
25. Моро, М.И. Методика обучения математике I-III классах [Текст] / М.И. Моро, А.М. Пышкало. - М.: Просвещение, 1978. – 321 с.
26. Остер, Г.Б. Задачник [Текст]/Г.Б.Остер. – М.: Спарк-М, 1995. – 116с.
27. Пойа, Д. Как решать задачу [Текст]/Д.Пойа. – М.: Учпедгиз, 1959. – 216 с.
28. Программы общеобразовательных учреждений. Начальные классы (1-4). Часть I. - М.: Просвещение, 2001. – 432 с.
29. Сорокин, П.И. Занимательные задачи по математике [Текст] / П.И.Сорокин. – М.: Просвещение, 1967. – 229 с.
30. Стойлова, Л.П. Математика [Текст]/Л.П. Стойлова.- М.: Академия, 2000. – С.226.
31. Стойлова, Л.П. Основы начального курса математики [Текст] / Л.П. Стойлова, А.М. Пышкало. – М.: Просвещение, 1988.– 320 с.
32. Труднев, В.П. Внеклассная работа по математике в начальной школе [Текст] /В.П. Труднев. – М.: Просвещение, 1975. – 335 с.
33. Труднев, В.П. Считай, смекай, отгадывай! [Текст]/В.П. Труднев. – М.: Просвещение, 2004. – С.128.
34. Учебное пособие по математике для педагогических факультетов. Под редакцией Мерзона- М.: Московский псих.-соц. институт, 1999. – С.28.
35. Формирование элементарных математических представлений у дошкольников / под редакцией А.А. Столяра. – М.: Просвещение, 1988. – 303 с.
36. Фридман, Л.М. Как научиться решать задачи [Текст]/Л.М. Фридман, Е.Н. Турецкий. – М.: Просвещение, 1989. – 192 с.
37. Эрдниев, П.М., Эрдниев Б.П. Теория и методика обучения математике в начальной школе [Текст]/П.М. Эрдниев, Б.П. Эрдниев. – М.: Педагогика, 1988. – 208 с.
|