Министерство образования и науки Российской Федерации
ГОУ ВПО “Татарский государственный гуманитарно-педагогический университет”
Институт педагогики и психологии
Кафедра математики и методики ее преподавания
Выпускная квалификационная работа
Использование занимательных игр в развитии познавательного интереса младших школьников на уроках математики
Выполнил: студент группы
Руководитель:
должность: ст.преподаватель, к.п.н
Казань 2009
Оглавление
Введение
Глава I Теоретические основы процесса формирования и развития познавательного интереса младших школьников на уроках математики
1.1 Историко-педагогический аспект проблемы формирования познавательного интереса в процессе обучения
1.2 Понятие «познавательный интерес», его структура
1.3 Взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике
1.4 Вывод по 1-ой главе
Глава II Развитие познавательного интереса к урокам математики младших школьников средствами использования занимательных дидактических игр
2.1 Дидактические игры, их виды
2.2 Особенности использования дидактических игр в 1 классе
2.3 Опытно-экспериментальная работа
2.4 Вывод по 2-ой главе
Заключение
Список использованной литературы
Приложения
Введение
Математика в начальных классах является основным учебным предметом. Младшие школьники усваивают систему важнейших математических понятий, овладевают умениями и навыками в области счета, письма, речи, без чего невозможно успешное обучение в школе. Велико воспитательное значение математики: она открывает младшим школьникам дидактические игры занимательного характера.
Как известно, знания, полученные без интереса, не становятся полезными. Поэтому одной из труднейших и важнейших задач дидактики как была, так и остается проблема воспитания интереса к учению.
Познавательный интерес в трудах психологов и педагогов изучен достаточно тщательно. Но все-таки остаются не решенными некоторые вопросы. Главный из них – как вызвать устойчивый познавательный интерес.
С каждым годом дети все равнодушнее относятся к учебе. В частности понижается познавательный интерес учащихся начальных классов к такому предмету как математика. Этот предмет воспринимается учащимися как скучный и совсем не интересный. В связи с этим учителями ведется поиск эффективных форм и методов обучения математике, которые способствовали бы активизации учебной деятельности, формированию познавательного интереса.
Реклама

Одна из возможностей развивать познавательный интерес учащихся к математике лежит в широком применении внеклассной работы по математике. Внеклассная работа по математике имеет мощный резерв для реализации такой задачи обучения, как повышение познавательного интереса, через все разнообразие форм ее проведения. Одной из таких форм является занимательная игра.
"Предмет математики настолько серьезен, что полезно не упускать случая сделать его немного занимательным " - сказал Б.Паскаль.
Познавательный интерес – избирательная направленность личности на предметы и явления окружающие действительность. Эта направленность характеризуется постоянным стремлением к познанию, к новым, более полным и глубоким знаниям. Систематически укрепляясь и развиваясь познавательный интерес становится основой положительного отношения к учению. Познавательный интерес носит поисковый характер. Под его влиянием у человека постоянно возникают вопросы, ответы на которые он сам постоянно и активно ищет. При этом поисковая деятельность школьника совершается с увлечением, он испытывает эмоциональный подъем, радость от удачи. Познавательный интерес положительно влияет не только на процесс и результат деятельности, но и на протекание психических процессов - мышления, воображения, памяти, внимания, которые под влиянием познавательного интереса приобретают особую активность и направленность. Познавательный интерес - это один из важнейших для нас мотивов учения школьников. Его действие очень сильно. Под влиянием познавательного интереса учебная работа даже у слабых учеников протекает более продуктивно. Познавательный интерес при правильной педагогической организации деятельности учащихся и систематической и целенаправленной воспитательной деятельности может и должен стать устойчивой чертой личности школьника и оказывает сильное влияние на его развитие. Познавательный интерес выступает перед нами и как сильное средство обучения. Классическая педагогика прошлого утверждала – ” Смертельный грех учителя – быть скучным”. Когда ребенок занимается из-под палки, он доставляет учителю массу хлопот и огорчений, когда же дети занимаются с охотой, то дело идет совсем по-другому. Активизация познавательной деятельности ученика без развития его познавательного интереса не только трудна, но практически и невозможна. Вот почему в процессе обучения необходимо систематически возбуждать, развивать и укреплять познавательный интерес учащихся и как важный мотив учения, и как стойкую черту личности, и как мощное средство воспитывающего обучения, повышения его качества. Познавательный интерес направлен не только на процесс познания, но и на результат его, а это всегда связано со стремлением к цели, с реализацией ее, преодолением трудностей, с волевым напряжением и усилием. Познавательный интерес – не враг волевого усилия, а верный его союзник. В интерес включены, следовательно, и волевые процессы, способствующие организации, протеканию и завершению деятельности. Таким образом, в познавательном интересе своеобразно взаимодействуют все важнейшие проявления личности.
Реклама

Занимательные игры отличаются эмоциональностью, вызывают у учащихся положительное отношение к урокам математики; способствуют активизации учебной деятельности; обостряют интеллектуальные процессы и главное, способствуют формированию познавательного интереса к предмету. Но следует заметить, что занимательная игра как форма классной работы применяется довольно таки редко, в связи с трудностями организации и проведения. Таким образом, большие образовательные, контролирующие, воспитывающие возможности (в частности возможность развития познавательного интереса) применения занимательной игры на уроках математики реализуются недостаточно.
А может ли занимательная игра являться эффективным средством развития познавательного интереса учащихся к математике? В этом и заключается проблема данного исследования.
Исходя из этой проблемы, можно определить цель исследования – обосновать эффективность использования дидактических игр в работе учителя начальных классов для формирования и развития познавательного интереса у учащихся к математике.
Объект исследования - процесс развития познавательного интереса у младших школьников на уроках математики.
Предмет исследования - развитие познавательного интереса у младших школьников на уроках математики средствами использования дидактических игр.
Гипотеза исследования состоит в следующем: повышению уровня познавательного интереса к урокам математики у младших школьников способствует включение в процесс обучения систематически проводящихся разнообразных дидактических игр.
Задачи:
- изучить теоретические основы формирования и развития познавательного интереса младших школьников;
- выявить особенности использования дидактических игр на уроках математики;
- разработать и провести опытно-экспериментальную работу с целью проверки рабочей гипотезы.
Методы исследования: изучение методической, психолого-педагогической литературы по рассматриваемой теме; наблюдение; анкетирование; тестирование.
Практическая значимость исследования состоит в том, что выводы и материалы исследования могут быть использованы студентами и педагогами учебных заведений, учителями начальной школы при планировании и организации уроков математики, внеклассных мероприятий, занятий математического кружка и других форм работы с учащимися.
Структура работы:
В соответствии с целями и задачами исследования выпускная квалификационная работа состоит из введения, 2 глав, включающих 6 параграфов, в том числе опытно-экспериментальную часть, заключения, списка используемой литературы, приложений.
В заключении обобщаются результаты исследования, формулируются выводы и практические рекомендации.
База исследования: 1 класс «Б» (экспериментальный) и 1 класс «А» (контрольный), школы № 2 п.г.т.Кукмор Республики Татарстан.
Глава I Теоретические основы процесса формирования и развития познавательного интереса младших школьников на уроках математики
1.1 Историко-педагогический аспект проблемы формирования познавательного интереса в процессе обучения
Проблема интереса к учению в истории русской педагогической мысли и в практике обучения выкристаллизовывалась постепенно под влиянием требований жизни. Социально-экономические изменения в России начиная со второй половины XVIII в. подводили к жизненно назревшим вопросам развития просвещения. К перестройке просвещения в России и поиску путей усвоения знаний, пригодных для развития в стране промышленности и торговли, с учётом, однако, интересов помещиков-крепостников, были привлечены образованнейшие для того времени люди, воспринявшие передовые идеи европейской педагогики, - И.И. Бецкой и Ф.И. Янкович. Идеи И.И. Бецкого создать сословные учебные заведения и вырастить в них «новую породу людей» выражали новое отношение к природе человека. Природу ребёнка нельзя разбудить, пока учение будет горестным, нужно приохотить детей к занятиям, вызвать у них любовь к учению. Практически руководя перестройкой образования в России, Бецкой доказывал это в уставных документах и в своих работах. Однако реализовать идею не удалось. Дальнейший поиск системы образования и обучения осуществлялся Ф.И. Янковичем. Янкович выступал за использование в обучении элементов занимательности, игры, оживляющих занятия. Он впервые увидел связь интереса к учению с нравственностью. Линия связи интереса с нравственным воспитанием прослеживается и во взглядах Н.И. Новикова. Он отождествлял любопытство с потребностью в учении. Условием развития любопытства Н.И. Новиков считал знание воспитателя сил и способностей, которые дают наблюдения за занятиями ребёнка «по натуральному побуждению», выражающему интерес, внимание к изучаемому. Реализовать первые подступы к проблеме интереса в обучении было трудно. В училищах, организованных Н.И. Новиковым и в народных училищах, основанных Ф.И. Янковичем, преобладали зубрёжка, побои, и дети стремились убегать с уроков, пропускали занятия по несколько месяцев. В первой половине XIX в. общественно-экономическое развитие России всё же привело к созданию в стране системы образования, требовавшей новой дидактической теории, которой в России в начале века ещё не было. Появляются отдельные, правда переводные, работы по педагогике. Впервые любопытство от любознательности отграничил В.Ф. Одоевский. Он считал, что свойственное детям любопытство при надлежащем руководстве может перерасти в любознательность, в страсть к познанию, развивающую умственную самостоятельность. В.Г. Белинский и А.И. Герцен были убеждены в том, что любознательность детей следует в первую очередь развивать при помощи естественных наук, книг, знакомящих с землёй, природой, которые сильнее всего могут заинтересовать детей, так как природа близка им. Для педагогических воззрений В.Г. Белинского и А.И. Герцена характерна связь интереса к познанию с интересом социальным. Но эта идея не могла найти своего воплощения, поскольку В.Г. Белинский писал в подцензурной России, а работы А.И. Герцена вообще были запрещены. И тем не менее передовая педагогическая мысль 60–70-х гг. XIX в. в решении вопросов воспитания и обучения не обходила стороной проблему интереса в обучении, несмотря на то, что социальных исследований по этой проблеме всё ещё не было. Обстоятельно, в контексте своей педагогической теории проблему интереса рассмотрел К.Д. Ушинский. В своей теории он психологически обосновал интерес в обучении. Глубокая психологическая основа всей педагогической теории К.Д. Ушинского и проблемы интереса усилили внимание к природосообразному развитию детей. Обострённая критика обучения и воспитания в период общественно- педагогического подъёма привела к идее пристального внимания к внутреннему миру ребёнка на основе его полной свободы. Эту точку зрения отразил в своих педагогических взглядах Л.Н. Толстой. Он справедливо считал, что интерес ребёнка может раскрыться лишь в условиях, не стесняющих проявление его способностей и наклонностей. Интерес в педагогических взглядах Толстого является центром всей педагогической работы. Важнейшее условие проявления интереса - это создание на уроке такой естественной, свободной атмосферы, которая вызывает подъём душевных сил ребёнка. Л.Н. Толстой всецело полагался на интересы детей, за учителем оставалось право лишь фиксировать увлечения детей, связанные с их природой. Н.А. Добролюбов и Н.Г. Чернышевский считали, что только воспитание, опирающееся на разумную свободу ребёнка, развивает его интересы и любознательность, укрепляет его ум и волю. С этих позиций Н.А. Добролюбов высоко оценивал школы Р. Оуэна, где учителя поддерживали и развивали интерес детей к учению. Но прогрессивные идеи трудно было применить на практике. Причин было много: неудовлетворительная подготовка учителей, особенно начальной школы, консерватизм учителей, перегруженность программ, тяжёлое материальное положение народного учителя. В начале XX в. отдельным изданием вышла работа по интересу в обучении А.И. Анастасиева. В этом исследовании весь процесс обучения раскрывался через призму интереса. После победы Октябрьской революции поиск новых путей учебно- воспитательной работы связывался с задачей воспитания поколений, способных строить коммунистическое общество. С марксистских позиций рассматривала проблему интереса Н.К. Крупская. Практическое применение прогрессивные идеи по проблеме интереса в обучении нашли в опыте педагогов А.С. Макаренко и С.Т. Шацкого. С.Т. Шацкий уделял самое серьёзное внимание проблеме интереса в обучении. Но С.Т. Шацкий не избежал противоречий: с одной стороны, как он считал, интерес - важный фактор активного усвоения ребёнком социального опыта, с другой - роль интереса он видел в приспособлении ребёнка к окружающей среде. А.С. Макаренко раскрывает некоторые методические приёмы поддержания и развития интереса: подсказка, вызывающая догадку, постановка интересного вопроса, введение нового материала, рассматривание иллюстраций, наталкивающих на вопросы, и т.д. Макаренко считал, что жизнь и труд ребёнка должны быть пронизаны интересом, что содержание образовательной работы определяется детским интересом. В диалектике воспитательного процесса А.С. Макаренко показал единство содержания, средств и методов воспитания, раскрыл логику воспитательного процесса, исходя из сочетания требований общественной жизни с интересами детского коллектива и интересами отдельной личности. Дальнейшая разработка проблемы интереса была связана с переходом на классно-урочную систему обучения. Ш.А. Амонашвили разрабатывал проблему интереса в обучении шестилеток. Интерес к учению слит со всей жизнедеятельностью младшего школьника: неосторожный поворот метода, однообразие приёма может расшатать интерес, который ещё очень хрупок. Лабораторией экспериментальной диалектики НИИ педагогики Грузии под руководством Ш.А. Амонашвили разработаны психолого - педагогические основы, заложенные в эксперименте по обучению шестилеток, накоплены приёмы стимулирования познавательных интересов детей (преднамеренные «ошибки» учителя, задачи на внимание, сочинительство сказок, задачи на сравнение и т.д.). Сегодня проблема интереса всё шире исследуется в контексте разнообразной деятельности учащихся, что позволяет творчески работающим учителям, воспитателям успешно формировать и развивать интересы учащихся, обогащая личность, воспитывать активное отношение к жизни.
Сегодня нужен человек не только потребляющий знания, но и умеющий их добывать. Нестандартные ситуации наших дней требуют от нас широты интереса. Интерес - это реальная причина действий, ощущаемая человеком как особо важная. Он является одним из постоянных сильнодействующих мотивов деятельности. Интерес можно определить как положительное оценочное отношение субъекта к его деятельности.
Как сильное и очень значимое для человека образование, интерес имеет множество трактовок в своих психологических определениях, он рассматривается как:
1)проявление его умственной и эмоциональной активности (С.Л.Рубинштейн);
особый сплав эмоционально-волевых и интеллектуальных процессов, повышающих активность сознания и деятельности человека (А.А.Гордон);
активное познавательное (В.Н. Мясинцев, В.Г. Иванов), эмоционально-познавательное (Н.Г.Морозова) отношение человека к миру;
специфическое отношение личности к объекту, вызванное сознанием его жизненного значения и эмоциональной привлекательности (А.Г.Ковалев).
Этот перечень трактовок интереса в психологии далеко не полон, но и сказанное подтверждает, что наряду с различиями выступает и известная общность аспектов, направленных на раскрытие феномена интереса, - его связи с различными психическими процессами, из которых особенно часто выделяют эмоциональные, интеллектуальные, регулятивные (внимание, воля), его включенность в различные личностные образования.
Особый вид интереса - интерес к познаниям, или, как его принято теперь называть, познавательный интерес. Его область - познавательная деятельность, в процессе которой происходит овладение содержанием учебных предметов и необходимыми способами или умениями и навыками, при помощи которых ученик получает образование.
Проблема интереса как важнейшего стимула развития личности теперь все больше привлекает к себе внимание, как педагогов, так и психологов.[4;с.45]
Интерес с психологической точки зрения, характеризуется подвижностью, изменчивостью, разнообразием оттенков и степеней развития. Большинство психологов относят интерес к категории направленностей, то есть к стремлениям личности к объекту или деятельности. Придавая особое значение познавательному интересу, психологи указывают на то, что под этим «интересом понимаются как интерес к содержанию, так и к процессу овладения знаниями».
С точки зрения С.Л.Рубинштейна и Б.Г.Ананьева психологические процессы, включенные в познавательный интерес, - это не сумма слагаемых, а особые связи, своеобразные взаимоотношения. Интерес – это «сплав» многих психических процессов, образующих особый тонус деятельности, особые состояния личности (радость от процесса учения, стремление углубиться в познание интересующего предмета, в познавательную деятельность, переживание неудач и волевые устремления к их преодолению).[7;с.33]
Познавательный интерес играет в педагогическом процессе главную роль. И. В. Метельский определяет познавательный интерес следующим образом: «Интерес – это активная познавательная направленность, связанная с положительным эмоционально окрашенным отношением к изучению предмета с радостью познания, преодолению трудностей, созданием успеха, с самовыражением развивающейся личности». [25;с.20]
Г. И. Щукина, специально занимавшаяся исследованием познавательного интереса в педагогике, определяет его следующим образом: «познавательный интерес выступает перед нами как избирательная направленность личности, обращенная к области познания, к ее предметной стороне и самому процессу овладения знаниями». [41;с.34]
У школьников одного и того же класса познавательный интерес может иметь разный уровень своего развития и характер проявлений, обусловленных различным опытом, особыми путями индивидуального развития.
Элементарным уровнем познавательного интереса можно считать открытый, непосредственный интерес к новым фактам, занимательным явлениям, которые фигурируют в информации, полученной учеником на уроке. На этой стадии – стадии любопытства ученик довольствуется только занимательностью того или иного предмета, той или иной области знаний. На этой ступени у учащихся еще не замечается стремления к познанию сущности.
Более высоким уровнем его является интерес к познаниям существенных свойств предметов и явлений, составляющих более глубокую часто невидимую их внутреннюю суть. Этот уровень, называемый стадией любознательности, требует поиска, догадки, активного оперирования имеющимися знаниями, приобретенными способами. Стадия любознательности характеризуется стремлением проникнуть за пределы видимого на ступени развития познавательного интереса. Школьнику свойственны эмоции удивления, радости познания. Ученик, включаясь по собственному побуждению в деятельность, наталкивается на трудности и сам начинает искать причины неудачи. Любознательность, становясь устойчивой чертой характера, представляет большую ценность для развития личности. Эта стадия, как показали исследования, характерны для младших подростков, которые еще не имеют достаточного теоретического багажа, чтобы проникнуть в суть и в глубь вещей, но уже оторвались от элементарных конкретных действий и становятся способными к самостоятельному дедуктивному подходу в изучении. [15;с.24]
Еще более высокий уровень познавательного интереса составляет интерес школьника к причино-следственным связям, к выявлению закономерностей, к установлению общих принципов явлений, действующих в различных условиях. Этот интерес характеризует собой подлинно познавательный интерес. Стадия познавательного интереса обычно связывается со стремлением ученика к разрешению проблемного вопроса. В центре внимания школьника становится не готовый материал учебного предмета и не сама по себе деятельность, а вопрос, проблема. Познавательный интерес, как особая направленность личности на познание окружающей действительности, характеризуется непрерывным поступательным движением. Содействует переходу школьника от незнания к знанию. Для познавательного интереса характерно напряжение мысли, усиления воли, проявление чувств, ведущие к преодолению трудностей в решении задач, к активным поискам ответа на проблемные вопросы.
Существует так же стадия теоретического интереса, связанная не только стремлением к познанию закономерностей, теоретических основ, но и с применением их в практике, появляется на определенном этапе развития личности и ее мировоззрения. Эта ступень характеризуется активным воздействием на мир, направленным на его переустройство, требует от личности не только глубоких знаний, она связана с формированием стойких ее убеждений. На эту ступень в состоянии подняться лишь старшие школьники, имеющие теоретическую основу для формирования научных взглядов, правильного миропонимания.
Эти ступени развития познавательного интереса: любопытство, любознательность, познавательный интерес, теоретический интерес помогает нам более или менее точно определить отношение ученика к предмету и степень влияния его на личность. И хотя эти стадии не все принимают и выделяются они чисто условно остаются общепризнанными.
Было бы ошибкой, однако, рассматривать указанные ступени познавательного интереса изолированно друг от друга. В реальном процессе они представляют собой сложнейшие сочетания и взаимосвязи.
Состояние заинтересованности, которое обнаруживает ученик на том или ином учебном занятии, проявляющееся под влиянием самых разнообразных сторон обучения (занимательность, расположение к учителю, удачный ответ, поднявший его престиж перед коллективом и т. д.), может быть временным, преходящим, не оставляющим глубокого следа в развитии личности ученика, в отношении школьника к учению. Но в условиях высокого уровня обучения, при целенаправленной работе учителя по формированию познавательных интересов это временное состояние заинтересованности может быть использовано, как отправная точка для развития пытливости, любознательности, стремления во всем руководствоваться научным подходом при изучении различных учебных предметов (искать и находить доказательства, читать дополнительную литературу, интересоваться последними научными открытиями и т. д.). [17;с.43]
Познавательный интерес психологи и педагоги изучают с различных сторон, но любое исследование рассматривает как часть общей проблемы воспитания и развития. Сегодня проблема интереса всё шире исследуется в контексте разнообразной деятельности учащихся, что позволяет творчески работающим учителям, воспитателям успешно формировать и развивать интересы учащихся, обогащая личность, воспитывать активное отношение к жизни.
1.2 Понятие «познавательный интерес», его структура
Познавательный интерес - это избирательная направленность личности на предметы и явления окружающие действительность. Эта направленность характеризуется постоянным стремлением к познанию, к новым, более полным и глубоким знаниям. Лишь тогда, когда та или иная область науки, тот или иной учебный предмет представляются человеку важными, значительными, он с особым увлечением занимается ими, старается более глубоко и основательно изучить все стороны тех явлений, событий, которые связаны с интересующей его областью знаний. В противном случае интерес к предмету не может носить характера подлинной познавательной направленности: он может быть случайным, нестойким и поверхностным.
Систематически укрепляясь и развиваясь познавательный интерес становится основой положительного отношения к учению. Познавательный интерес носит поисковый характер. Под его влиянием у человека постоянно возникают вопросы, ответы на которые он сам постоянно и активно ищет. При этом поисковая деятельность школьника совершается с увлечением, он испытывает эмоциональный подъем, радость от удачи. Познавательный интерес положительно влияет не только на процесс и результат деятельности, но и на протекание психических процессов - мышления, воображения, памяти, внимания, которые под влиянием познавательного интереса приобретают особую активность и направленность.
Характерной особенностью познавательного интереса является и его волевая направленность. Познавательный интерес направлен не только на процесс познания, но и на результат его, а это всегда связано со стремлением к цели, с реализацией ее, преодолением трудностей, с волевым напряжением и усилием. Познавательный интерес - не враг волевого усилия, а верный его союзник. В познавательном интересе своеобразно взаимодействуют все важнейшие проявления личности.
Познавательный интерес - это один из важнейших мотивов учения школьников. Под влиянием познавательного интереса учебная работа даже у слабых учеников протекает более продуктивно. Этот мотив окрашивает эмоционально всю учебную деятельность подростка. В то же время он связан с другими мотивами (ответственностью перед родителями и коллективом и др.). Познавательный интерес как мотив учения побуждает ученика к самостоятельной деятельности, при наличии интереса процесс овладения знаниями становится более активным, творческим, что в свою очередь, влияет на укрепление интереса. Самостоятельное проникновение в новые области знания, преодоление трудностей вызывает чувство удовлетворения, гордости, успеха, то есть создает тот эмоциональный фон, который характерен для интереса. [7;с.44]
Познавательный интерес при правильной педагогической и методической организации деятельности учащихся и систематической и целенаправленной воспитательной деятельности может и должен стать устойчивой чертой личности школьника и оказывает сильное влияние на его развитие. Как черта личности познавательный интерес проявляется во всех обстоятельствах, находит применение своей пытливости в любой обстановке, в любых условиях. Под влиянием интереса развивается мыслительная активность, которая выражается во множестве вопросов, с какими школьник, например, обращается к учителю, к родителям, взрослым, выясняя сущность интересующего его явления. Отыскание и чтение книг в интересующей области, выбор определенных форм внеклассной работы, способных удовлетворить его интерес, - все это формирует и развивает личность школьника.
Познавательный интерес выступает и как сильное средство обучения. Характеризуя интерес как средство обучения, следует оговориться, что интересное преподавание - это не развлекательное преподавание, насыщенное эффективными опытами, демонстрациями красочных пособий, занимательными задачами и рассказами и т. д., это даже не облегченное обучение, в котором все рассказано, разъяснено и ученику остается только запомнить. Интерес как средство обучения действует только тогда, когда на первый план выступают внутренние стимулы, способные удержать вспышки интереса, возникающие при внешних воздействиях. Новизна, необычность, неожиданность, странность, несоответствие ранее изученному, все эти особенности способны не только вызвать мгновенный интерес, но и пробудить эмоции, порождающие желание изучить материал более глубоко, т. е. содействовать устойчивости интереса. Классическая педагогика прошлого утверждала – ” Смертельный грех учителя – быть скучным”. Когда ребенок занимается из-под палки, он доставляет учителю массу хлопот и огорчений, когда же дети занимаются с охотой, то дело идет совсем по-другому.
Активизация познавательной деятельности ученика без развития его познавательного интереса не только трудна, но практически и невозможна. Вот почему в процессе обучения необходимо систематически возбуждать, развивать и укреплять познавательный интерес учащихся и как важный мотив учения, и как стойкую черту личности, и как мощное средство воспитывающего обучения, повышения его качества.
Быть внимательным к каждому ребенку. Уметь увидеть, подметить у ученика малейшую искру интереса к какой-либо стороне учебной работы, создавать все условия для того, чтобы разжечь ее и превратить в подлинный интерес к науке, к знаниям - в этом задача учителя, формирующего познавательный интерес.
Таким образом, познавательный интерес может рассматриваться как один из важнейших мотивов учения, как устойчивая черта личности и как сильное средство обучения. В процессе же обучения важно развивать и укреплять познавательный интерес и как мотив учения, и как черту личности, и как средство обучения. При этом нужно помнить, что существуют разные стадии развития познавательного интереса, знать их особенности, признаки. А для того чтобы учитель мог формировать познавательный интерес в какой-либо деятельности он должен знать основные формы и пути активизации познавательного интереса, учесть все необходимые для этого условия. [32;с.75]
Опираясь на огромный опыт прошлого, на специальные исследования и практику современного опыта, можно говорить об условиях, соблюдение которых способствует формированию, развитию и укреплению познавательного интереса учащихся:
Первое условие состоит в том чтобы, осуществлять максимальную опору на активную мыслительную деятельность учащихся. Главной почвой для развития познавательных сил и возможностей учащихся, как и для развития, подлинно познавательного интереса, являются ситуации решения познавательных задач, ситуации активного поиска, догадок, размышления, ситуации мыслительного напряжения, ситуации противоречивости суждений, столкновений различных позиций, в которых необходимо разобраться самому, принять решение, встать на определённую точку зрения.
Второе условие предполагает обеспечение формирования познавательных интересов и личности в целом. Оно состоит в том, чтобы вести учебный процесс на оптимальном уровне развития учащихся. Путь обобщений, отыскание закономерностей, которым подчиняются видимые явления и процессы, — это путь, который в освещении множества запросов и разделов науки способствует более высокому уровню обучения и усвоения, так как опирается на максимальный уровень развития школьника. Именно это условие и обеспечивает укрепление и углубление познавательного интереса на основе того, что обучение систематически и оптимально совершенствует деятельность познания, её способов, её умений. В реальном процессе обучения учителю приходится иметь дело с тем, чтобы постоянно обучать учащихся множеству умений и навыков. При всём разнообразии предметных умений выделяются общие, которыми учение может руководствоваться вне зависимости от содержания обучения, такие, например, как умение читать книгу (работать с книгой), анализировать и обобщать, умение систематизировать учебный материал, выделять единственное, основное, логически строить ответ, приводить доказательства и т.д. Эти обобщённые умения основаны на комплексе эмоциональных регулярных процессов. Они и составляют те способы познавательной деятельности, которые позволяют легко, мобильно, в различных условиях пользоваться знаниями и за счёт прежних приобретать новые.
Эмоциональная атмосфера обучения, положительный эмоциональный тонус учебного процесса - третье важное условие. Благополучная эмоциональная атмосфера обучения и учения сопряжена с двумя главными источниками развития школьника: с деятельностью и общением, которые рождают многозначные отношения и создают тонус личного настроения ученика. Оба эти источника не изолированы друг от друга, они всё время переплетаются в учебном процессе, и вместе с тем стимулы, поступающие от них, различны, и различно влияние их на познавательную деятельность и интерес к знаниям, другие - опосредованно. Благополучная атмосфера учения приносит ученику желание быть умнее, лучше и догадливей. Именно это стремление ученика подняться над тем, что уже достигнуто, утверждает чувство собственного достоинства, приносит ему при успешной деятельности глубочайшее удовлетворение, хорошее настроение, при котором работается скорее, быстрее и продуктивней. Создание благоприятной эмоциональной атмосферы познавательной деятельности учащихся - важнейшее условие формирования познавательного интереса и развития личности ученика в учебном процессе. Это условие связывает весь комплекс функций обучения - образовательной, развивающей, воспитывающей и оказывает непосредственное и опосредованное влияние на интерес. Из него вытекает и четвёртое важное условие, обеспечивающее благотворное влияние на интерес и на личность в целом.
Четвертым условием является благоприятное общение в учебном процессе. Эта группа условий отношения «ученик - учитель», «ученик - родители и близкие», «ученик - коллектив». К этому следует добавить некоторые индивидуальные особенности самого ученика, переживание успеха и неуспеха, его склонности, наличие других сильных интересов и многое другое в психологии ребенка. Каждое из этих отношений может повлиять на заинтересованность ученика, как в положительном, так и в отрицательном направлении. Всеми этими отношениями и, прежде всего отношением «учитель - ученик» управляет учитель. Его требовательное и в тоже время заботливое отношение к ученику, его увлеченность предметом и стремление подчеркнуть его огромное значение - определяет отношение ученика к изучению данного предмета. К этой группе условий следует способности ученика, а также успех, достигнутый им в результате упорства и настойчивости.
Итак, выше были рассмотрены одни из самых главных условий формирования познавательного интереса. Соблюдение всех этих условий способствует формированию познавательного интереса при обучении школьным предметам, в том числе и математике.
1.3 Взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике
Познавательный интерес, как и всякая черта личности и мотив деятельности школьника, развивается и формируется в деятельности, и, прежде всего, в учении.
Успех учителя в процессе обучения зависит в первую очередь от того, насколько ему удалось заинтересовать учащихся своим предметом. Но интерес не может возникнуть сам по себе, учителю нужно принять в этом участие, поспособствовать. Как это сделать? Следует заметить, что успеваемость учащихся по предмету не всегда является показателем наличия у ученика познавательного интереса к нему. Ребенок может получать только отличные оценки и это может свидетельствовать только о его старательности или о том, что ему легко дается математика. О наличии у него познавательного интереса к математике утверждать нельзя. В то же время, ученик, не отличающийся успеваемостью по математике, может проявлять интерес к предмету, ему нравиться заниматься на уроке математики. Работа учителя в классе заключается в том, чтобы выявить таких учеников, развить и сформировать у них устойчивый познавательный интерес. Педагог должен поддержать таких учеников, разнообразить их учебную деятельность, привлечь к внеклассной работе по математике. Возможно, таким детям понравиться решать нестандартные математические задачи, в которых они смогут проявить свои математические способности. Добившись успеха, ученик поднимется не только в своих глазах, но в глазах одноклассников. Все это вдохновит его на дальнейшее более серьезное изучение математики. [24;с.56]
Чтобы заинтересовать как можно больше учащихся математикой, учителю нужно использовать в обучении математике различные формы, знать основные пути формирования познавательного интереса. Формирование познавательных интересов учащихся в обучении может происходить по двум основным каналам, с одной стороны само содержание учебных предметов содержит в себе эту возможность, а с другой – путем определенной организации познавательной деятельности учащихся.
Первое, что является предметом познавательного интереса для школьников – это новые знания о мире. Вот почему глубоко продуманный отбор содержания учебного материала, показ богатства, заключенного в научных знаниях, являются важнейшим звеном формирования интереса к учению. Каковы же пути осуществления этой задачи? Прежде всего, интерес возбуждает и подкрепляет такой учебный материал, который является для учащихся новым, неизвестным, поражает их воображение, заставляет удивляться. Удивление - сильный стимул познания, его первичный элемент. Удивляясь, человек как бы стремится заглянуть вперед. Он находится в состоянии ожидания чего-то нового.
Но познавательный интерес к учебному материалу не может поддерживаться все время только яркими фактами, а его привлекательность невозможно сводить к удивляющему и поражающему воображение. Новое и неожиданное всегда в учебном материале выступает на фоне уже известного и знакомого. Вот почему для поддержания познавательного интереса важно учить школьников умению в знакомом видеть новое. Такое преподавание подводит к осознанию того, что у обыденных, повторяющихся явлений окружающего мира множество удивительных сторон, о которых он сможет узнать на уроках.
Все значительные явления жизни, ставшие обычными для ребенка в силу своей повторяемости, могут и должны приобрести для него в обучении неожиданно новое, полное смысла, совсем иное звучание. И это обязательно явится стимулом интереса ученика к познанию. Именно поэтому учителю необходимо переводить школьников со ступени его чисто житейских, достаточно узких и бедных представлений о мире - на уровень научных понятий, обобщений, понимания закономерностей. Интересу к познанию содействует также показ новейших достижений науки. Сейчас, больше чем когда-либо, необходимо расширять рамки программ, знакомить учеников с основными направлениями научных поисков, открытиями. Все это можно осуществлять как на уроке математике, так и во внеклассной работе по математике.
Есть и другие направления развития интереса у школьников к математике, например использование научной фантастики. Задачи так же могут служить средством развития познавательного интереса. Содержание задач, их занимательная фабула, связь с жизнью незаменимы при обучении математике. Занимательность создает заинтересованность, рождает чувство ожидания, побуждает любопытство, любопытство переходит в любознательность и побуждает интерес к решению математических задач, к самой математике. К содержательной стороне задачи относится и ее новизна, достигаемая за счет включения сведений, связанных с жизнью. Повышают интерес к математике и задачи, содержащие факты из жизни конкретных исторических личностей, сведения из истории математики. Вообще, включение сведений из истории науки в занятия способствуют более сознательному усвоению учебного материала, развитию интереса у школьников к математике. Новизна задач также может достигаться путем реализации предметных связей. Также для развития интереса к математике можно использовать задачи и упражнения, содержащие ошибки. Такие задачи приучают школьников обращать внимание на необходимость строгих логических рассуждений. Умение решать задачи является одним из показателей уровня математического развития учащихся, глубины усвоения имеющихся у них знаний. [26;с.73]
Далеко не все в учебном материале может быть для учащихся интересно. И тогда выступает еще один, не менее важный источник познавательного интереса – сам процесс деятельности. Что бы возбудить желание учиться, нужно развивать потребность ученика заниматься познавательной деятельностью, а это значит, что в самом процессе ее школьник должен находить привлекательные стороны, что бы сам процесс учения содержал в себе положительные заряды интереса. Так эпизодическое использование игровых ситуаций, проведение в виде игр уроков и внеклассной работы своей не традиционностью и занимательностью повышают интерес учащихся к предмету.
Разнообразив содержание занятий по математике, как внеклассных, так и самих уроков, изменяя форму их приведения и учтя все условия формирования познавательного интереса, можно способствовать его развитию у большого числа учащихся.
Современное содержание математического образования направлено главным образом на интеллектуальное развитие младших школьников, формирование культуры и самостоятельности мышления.
Мы убедились в том, что наилучшее иллюстрирование заставляет ученика применить рассуждение, т. е. логические средства исследования, способствующие развитию мыслительных операций. Достаточная подготовленность к мыслительной деятельности снимает психологические нагрузки в учении, предупреждает неуспеваемость.
Мышление базируется на знаниях ребенка. Приведем примеры заданий на развитие мышления, которые мы успешно выполняем на уроках с учащимися.
Умение делать обобщения формируется на логических заданиях, включающих по 2 – 3 изменяющихся признака. Можно упражнять учащихся в поиске закономерностей, они выполняют задания следующего вида:
Нарисовать недостающий домик, не нарушая закономерности и т.п.
Считаю, что у ученика должна быть возможность сделать открытие, возможность творческой деятельности – это стимул учебного процесса, востребованный личностью обучающегося.
1.4 Вывод по 1-ой главе
Итак, мы рассмотрели в первой главе историко-педагогический аспект проблемы формирования познавательного интереса в процессе обучения;
понятие «познавательный интерес», его структура; взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике. В связи с этим можно сделать следующие выводы:
Познавательный интерес психологи и педагоги изучают с разных сторон, но любое исследование рассматривает интерес как часть общей проблемы воспитания и развития.
Познавательный интерес – это избирательная направленность личности на предметы и явления окружающей действительности.
Познавательный интерес можно рассматривать с разных сторон: как мотив учения, как устойчивую черту личности, как сильное средство обучения. Для того чтобы активизировать учебную деятельность школьника нужно систематически возбуждать, развивать и укреплять познавательный интерес и как мотив, и как стойкую черту личности, и как мощное средство обучения.
Структура. Существует четыре уровня развития познавательного интереса. Это любознательность, любопытство, познавательный интерес и теоретический интерес. Учителю нужно уметь определять, на какой стадии развития познавательный интерес у отдельных учащихся, для того чтобы способствовать укреплению интереса к предмету и его дальнейшему росту.
Существует определенная взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике.
Глава II Развитие познавательного интереса к урокам математики младших школьников средствами использования занимательных дидактических игр
2.1 Дидактические игры, их виды
В отличие от других видов деятельности игра содержит цель в самой себе; посторонних и отдаленных задач в игре ребенок не ставит и не решает. Игра часто и определяется как деятельность, которая выполняется ради самой себя, посторонних целей и задач не преследует. Следует иметь в виду, что по мере развития игр (от забав до сюжетно-ролевых, творческих) на определенном этапе появляется цель. Игровые действия становятся целесообразными: приступая к строительству «туннеля» в «горах» или к лечению «больного», ребенок знает, что и как он будет делать и что получится в результате игры. Точно так же и начиная игру в волейбол, футбол, дети ставят цель - выиграть. Но как в первом, так и во втором случае цель не выходит за рамки игры, заключена в ней самой и никаких посторонних задач в ней не ставится и не решается. [25;с.48]
Однако если для воспитанника цель - в самой игре, то для воспитателя, организующего игру, есть и другая цель - развитие детей, усвоение ими определенных знаний, формирование умений, выработка тех или иных качеств личности. В этом, между прочим, одно из основных противоречий игры как средства воспитания: с одной стороны - отсутствие цели в игре, а с другой - игра - есть средство целенаправленного формирования личности.
В наибольшей степени это проявляется в так называемых дидактических играх. Характер разрешения этого противоречия и определяет воспитательную ценность игры: если достижение дидактической цели будет осуществлено в игре как деятельности, заключающей цель в самой себе, то воспитательная ее ценность будет наиболее значимой. Если же дидактическая задача решается в игровых действиях, целью которых и для их участников является решение этой дидактической задачи, то воспитательная ценность игры будет минимальной.
О целесообразности использования игры в обучении существуют различные мнения. Учитывая большую сложность современного содержания образования и вообще то, что учение - дело серьезное, некоторые считают, что в обучении игре нет места. Но более обоснованным является все-таки другое мнение, сторонники которого утверждают, что обучение без игры не решит всех стоящих перед ним задач. Дело в том, что задачи обучения значительно шире, чем сообщение ученикам определенной суммы знаний и выработка умений применять эти знания. Главная задача обучения - подготовка детей к жизни. А в период ученичества дети фактически лишь в игре получают возможность трансформации окружающего мира в соответствии со своими желаниями, и, кроме того, игра, как справедливо утверждает Д.Брунер, является источником удовольствия для ребенка, она способствует его безболезненной адаптации к условиям социальной жизни в дальнейшем. Особая ценность игры состоит в том, что «...игра означает для нас трансформацию окружающего мира согласно нашему желанию, тогда как учение изменяет нас самих для лучшей адаптации к внешним условиям». Отметим, что Я.А. Коменский очень высоко оценивал роль игры в обучении. Он писал в «Автобиографии»: «Весь мой метод направлен на то, чтобы школьная подневольшина превратилась в игру и забаву».
И действительно, игра помогает активизировать учащихся в обучении, преодолевать скуку, уходить от шаблонных решений интеллектуальных и поведенческих задач, стимулирует инициативу и творчество.
Все игры, которые используются в дидактических целях, можно разделить на два вида в зависимости от основного содержания игровых действий. В одном случае основу содержания игры составляет дидактический материал, действия с которым облекаются в игровую форму. Например, дети, разделившись на команды, соревнуются в скорости счета или нахождения ошибок в словах, вспоминании дат исторических событий и т.п. Они выполняют обычные учебные действия считают, исправляют ошибки, вспоминают даты, - но выполняют эти действия ветре.
В другом случае дидактический материал вводится как элемент в игровую деятельность, которая является как по форме, так и по содержанию основной. Так, в игру-драматизацию со сказочным сюжетом, где каждый играет роль, определенную содержанием сказки, может быть внесен дидактический материал: некоторые знания по географии, биологии, истории, математике или другим предметам. Дети играют роли Буратино, Незнайки, Красной Шапочки, Бабы-яги и упражняются в счете, узнают расположение частей света или получают сведения о строении растений. [19;с.65]
Ясно, что во втором случае дидактическая «нагрузка» значительно меньшая, чем в первом. Но это оправдывается тем, что на первый план выдвигается не усвоение дидактического материала, а воспитательные задачи, использование знаний в различных ситуациях или предварительное ознакомление с новыми знаниями. Такие игры используются чаще во внеурочное время и на уроках в начальных классах для отдыха детей от напряженной интеллектуальной работы.
В начальных классах уже сама постановка учебной задачи для детей может осуществляться с использованием игровых моментов. Так, учитель может обратиться к детям от имени Буратино и Незнайки с просьбой вспомнить буквы и какие звуки обозначают эти буквы и т.п.
При изучении нового материала в дидактические игры в начальных классах вносятся моменты творчества. Так, С.И.Волкова рекомендует при изучении в III классе геометрических фигур стимулировать составление детьми изображений предметов из фигур, с которыми они познакомились.
Использование творческой игры на уроках русского языка организуется с целью расширения знаний детей, а главное - развития способностей самостоятельного их приобретения и использования в новых ситуациях. На занятиях русским языком для этого используют включение в игру работы со словарями, сочинения на свободную тему. На уроках математики - решение нестандартных задач, задач с неполными данными и т.д.
Естественно, чаще всего дидактические игры используются при учете знаний. Так, на уроке учета знаний по математике класс, делится на несколько команд, которые, соревнуясь, выполняют те или иные задания: математический диктант, решение задач по вариантам, решение примеров «цепочкой» на доске и т.д. Для учета результатов может быть сформировано жюри или назначены арбитры, эксперты и т.д. Командам могут быть даны сказочные, фантастические или просто интересные детям названия, могут быть введены в структуру и другие игровые символы.
В средних классах игры на уроках используются реже, чем в младших, в связи с тем, что перед подростками в обучении стоят более сложные задачи, да и сами подростки обладают, безусловно, большей способностью к систематическому целенаправленному труду. К традиционным соревнованиям, конкурсам, олимпиадам в 90-е гг. добавились игры по типу популярных телепередач:
«Что? Где? Когда?», «Поле чудес», «Звездный час», «Аукцион» и др. В них сохранилась соревновательно-конкурсная основа, изменилось лишь игровое оформление. Так, на уроках химии (например, на последнем уроке первого и второго полугодия) можно провести химические турниры, в которых - примут участие все школьники, изучающие химию.
Задания для конкурсов составляются так, чтобы, учащиеся продемонстрировали умение выразить химические знания в стихах, придумать и отгадать химические рифмованные загадки, ребусы, составить художественную презентацию какого-либо химического явления, класса химических соединений и др.
Большими обучающими возможностями располагают игры-драматизации типа «Корректор», «Редакция» на уроках русского языка или «Парламент», «Демократия» и др. на уроках истории.
Отметим, что Я.Коменский использовал игру в обучении. Он писал: «Я составил из первых 20 глав «Двери языков» первое представление, отобрав для него 52 дворянских юношей. ... Наши актеры играли свои роли так умело, что мы смотрели с изумлением. Ибо те, которые прежде едва могли выдержать взгляд взрослого человека и ничего не могли сказать без заикания, держали себя с пристойной свободой» («Автобиография»).
В современных условиях на уроках кроме игр-соревнований и драматизации проводят игры-имитации, моделирующие определенные отношения реального мира.
Ю.З.Гильбух описывает уроки-игры, характеризуя их такими положительными качествами, как ярко выраженная мотивация деятельности, добровольность участия и подчинения правилам, заинтриговывающая неопределенность исхода и более высокая по сравнению с обычными уроками обучающая, развивающая и воспитательная результативность. Автор разделяет их на учебно-ролевые и соревновательные. Для первых характерно максимальное включение воображения. Они разделяются на несколько видов:
1) с принятием учащимися определенных ролевых функций масок (по типу «Следствие ведут знатоки», «Круглый стол», «Суд» и т. п.);
2) с использованием сказочного сюжета (чаще всего в младших классах - «Волшебник мягкий знак», «Части речи», «Гласные и согласные»);
3) с фантазированием (например, на уроке-зачете по математике в игре «Мы - альпинисты» нужно взять «эту» высоту);
4) деловые игры - основаны на проигрывании не художественных, а профессиональных ролей; моделируются условия профессиональной деятельности, например, в начальных классах на уроке русского языка может быть проведена игра «Редакция».
Для использования всех игр в обучении характерна общая структура учебного процесс а, включающая четыре этапа:
1. Ориентация: учитель представляет тему, дает характеристику игры, общий обзор ее хода и правил.
2. Подготовка к проведению: ознакомление со сценарием, распределение ролей, подготовка к их исполнению, обеспечение процедур управления игрой.
3. Проведение игры: учитель следит за ходом игры, контролирует последовательность действий» оказывает необходимую помощь, фиксирует результаты.
4. Обсуждение игры: дается характеристика выполнения действий, их восприятия участниками, анализируются положительные и отрицательные стороны хода игры, возникшие трудности, обсуждаются возможные пути совершенствования игры, в том числе изменения ее правил. [31;с.44]
Конечно, использование игры в обучении связано с рядом проблем, и прежде всего с меньшей обучающей эффективностью игры по сравнению с обычной учебной работой, основу которой составляет учение как вид специальной деятельности учащихся, направленной на усвоение знаний, формирование умений и навыков. К тому же далеко не все учителя в достаточной мере знакомы с учебными играми, в школах нередко не хватает оборудования и материалов для проведения игр, немаловажной является и проблема обеспечения дисциплины, должного порядка в ходе игры по причине повышенной оживленности, эмоциональности учащихся. Однако глубокая продуманность учебной цели, обоснованный отбор содержания учебного материала и обеспечение высокого уровня включенности всех учащихся в игру, в которой ключевые роли получают не только сильные в учении, позволяют преодолеть эти и другие проблемы.
В последние десятилетия медленно, но достаточно настойчиво в школьную практику начали внедряться компьютерные игры. Эпизодичность использования компьютера на большинстве уроков в настоящее время вообще создает обстановку игры даже в том случае, если учащиеся работают по обучающим программам. Однако существуют и специальные игровые программы по различным учебным предметам: биологии, химии и др. Так, например, по истории есть такие программы, как «Цивилизация», «Центурион», «Аустерлиц» и др. Учитель, хорошо владеющий техникой работы с компьютером, может сам составлять игровые, контрольные и обучающие программы или программы с игровыми элементами.
Один из пионеров применения компьютеров в обучении С.Пейперт так описывает возможности использования компьютерных игр в учебном процессе: «На телевизионном экране... появляется цветная мультипликация. Вы можете сами нарисовать ее... По вашему желанию на экране может возникнуть палитра цветов, и вы можете выбрать цвет, которым станете рисовать. Цвет сохранится до тех пор, пока вы сами не пожелаете его изменить. Конечно, пока вы рисуете на экране, этот процесс по своим возможностям мало чем отличается от традиционных способов рисования, но различие становится принципиальным, когда вы решаете поработать над своим рисунком. На языке компьютера вы можете «говорить» с ним о своем рисунке. Вы можете попросить его изменить цвет или превратить рисунок в движущуюся картинку, заставить получившиеся два изображения вращаться в разные стороны,... заменить цветовую палитру на звуковую и «нарисовать» музыкальный фрагмент. ...Не надо много рассуждать, чтобы увидеть развлекательную сторону этого процесса. Но работа на компьютере - это не только забава. Это устройство позволяет превратить учение в весьма плодотворный процесс. Работая с электронной чертежной доской, дети учатся говорить на языке постоянно меняющихся форм ... меняющихся скоростей, на языке процессов и технологий».
К сожалению, на пути внедрения и распространения этих игр в обучении стоит чрезвычайно большое и мощное препятствие недостаток средств, отсутствие экономической базы, которая обеспечила бы каждого ребенка достаточно совершенным персональным компьютером, включенным в единую коммуникационную сеть. Это в значительной мере является и препятствием для разработки игровых программ и методики их использования при изучении различных учебных дисциплин: ведь не только у учеников нет персональных компьютеров, нет их и у учителей. Однако даже эпизодическое использование компьютера и приобщение детей к компьютерным играм если и не вводит их в мир современных технологий, то хотя бы показывает характер отношений человека с техникой в обществе будущего.
Одним из известных нетрадиционных видов урока является грамматическая игра (кроссворд, таящий в себе большие возможности для развития творческих способностей ребенка, тренировки памяти. На уроках кроссворды целесообразны не для проверки эрудиции учащихся, а для лучшего усвоения ими фактического материала. Логические задания кроссвордов подбираются с возрастными и психологическими особенностями учащихся. Способов зашифровки много, однако наибольший интерес у учащихся младших классов вызывают игры, зашифрованные с помощью загадок, требующих от ребенка сообразительности, поэтической выдумки. Загадки учат детей говорить ярко, образно. Они обогащают память детей подлинными жемчужинами родного языка. Назначение загадки состоит в выработке у учащихся внимания и акцентирования его на изучаемом материале (для пополнения словарного запаса детей, знакомства с лексическим значением слова, развития слуховой, а позднее зрительной памяти, выработки орфографической зоркости). Расширяя кругозор детей, знакомя их с окружающим миром, развивая и обогащая речь, загадки имеют неоценимое значение в формировании способности к творчеству: логического мышления (способность к анализу, синтезу, сравнению, сопоставлению), элементов эвристического мышления (способность выдвигать гипотезы, ассоциативность, гибкость, критичность мышления). Вот что писал по этому поводу К.Д.Ушинский: «Загадку я помещал не с той целью, чтобы ребенок отгадал сам загадку, хотя это часто может случиться, так как многие загадки просты; но для того, чтобы доставить уму ребенка полезное упражнение; приладить загадку, дать повод к интересной и полной классной беседе, которая закрепится в уме ребенка именно потому, что живописная и интересная для него загадка заляжет прочно в его памяти, увлекая за собой все объяснения, к ней привязанные». Процесс отгадывания, по мнению современных педагогов, является своеобразной гимнастикой, мобилизующей и тренирующей умственные силы ребенка. Отгадывание загадок оттачивает и дисциплинирует ум, приучая детей к четкой логике, к рассуждению и доказательству. Отгадывание загадок можно рассматривать как процесс творческий, а саму загадку (как творческую задачу). Поддержание познавательной активности учащихся в ходе контроля за уровнем знаний (важное условие успешности учебного процесса). Однако известно, что повторное воспроизведение детьми учебного материала, будучи важным в плане закрепления и контроля, снижает интерес к предмету, если проводится дублирующим образом и в форме простого повторения. Оживить опрос и активизировать в процессе его работу учащихся могут занимательные формы проверки усвоения фактического материала (кроссворды). Работать с ними можно с первого класса. Первоначально, вводя кроссворды в свою практику, следует объяснить учащимся, как их нужно решать. Лучше всего сделать это сначала совместно со школьниками, а затем постепенно предоставлять ребятам большую самостоятельность. Относительную трудность при использовании кроссвордов представляет их вычерчивание. Можно предварительно начертить кроссворд и написать текстовое пояснение на доске. Более целесообразным представляется показ его проекции через эпидиаскоп или кодоскоп. Можно наложить на кроссворд просвечивающий лист бумаги и таким образом вписать ответ без предварительного вычерчивания. Можно использовать кроссворды в виде кармашков, лицевая часть которых представляет собой трафарет с прорезями вместо букв, а на изнаночной стороне напечатаны задания для решения. Внутри кармашка вложен чистый листок с фамилией ученика. Такой кармашек позволяет многократно использовать одну и ту же сетку-решетку кроссворда для индивидуальной работы. Тематические кроссворды можно использовать как для фронтальной, так и для индивидуальной работы с учащимися. [12;с.34]
В современных работах рассматриваются различные формы дидактических игр, подразделяющиеся соответственно на три типа:
1)Прямое знакомство детей со средствами и способами познания или отражения окружающей действительности.
2)Передача информации от детей – взрослым, когда дети действуют самостоятельно, а взрослый наблюдает за их деятельностью.
3)Равноправный поиск взрослыми и детьми как субъектами деятельности решения проблемы в ходе наблюдения, обсуждения или экспериментирования.
Целесообразное сочетание игровой и трудовой деятельности в образовательном процессе приобретает особое значение в духовном развитии детей младшего школьного возраста, обособление которой от игры происходит постепенно и представляет собой итог естественного развития игровой деятельности детей.
В каждом виде изучения вычислений можно использовать игровые формы. Например, такие игры:
ромашка;
магические квадраты;
занимательные рамки;
составим поезд;
лестница;
угадай число;
почтовый ящик;
магазин;
угадай слово;
радисты и др.
Предлагаемые уроки-путешествия, уроки-экскурсии, уроки- игры в основном будут способствовать закреплению и расширению знаний и представлений, полученных на уроках, проходящих в классе с использованием заданий учебника. Исключение составляет материал, связанный с объектами трехмерного пространства, который входит в программу первого класса, но, в силу своей специфики, не отражен на страницах учебника.
Урок-путешествие по теме "Наши встречи с математикой". Урок желательно провести в окрестностях школы, проложив маршрут так, чтобы можно было посетить несколько разных магазинов, пройти мимо домов разной высоты, перейти или хотя бы посмотреть на улицы разной ширины. Во время путешествия дети измеряют отдельные, выбранные учителем, отрезки пути шагами, считают повороты налево и направо.
Желательно, чтобы учитель при участии детей составил план пройденного пути.
Целью данного урока является ознакомление с понятием натурального числа, и формирование абстрактного мышления – предметы в мире отличаются, но их количество можно выразить через те же самые числа.
Задачи урока: 1) заинтересовать детей математикой; 2) дать понятие натурального числа; 3) дать навыки счета и сравнения чисел между собой.
Урок-игра по теме "Ориентация в пространстве". Урок проводится на свежем воздухе или в помещении, которое позволит назвать большое количество предметов в любом названном учителем направлении - слева, справа, сзади, спереди, вверху, внизу, перед, за. Класс разбивается на 2 команды, которые попеременно называют предметы, расположенные в заданном направлении. Команда, которая не смогла назвать предмет, отдает фант. В конце игры фанты разыгрываются. В процессе игры желательно несколько раз менять местоположение команд, что позволит рассмотреть положение предметов с разных позиций.
Целью данного урока является ознакомление с основными координатами пространства.
Задачи урока: 1) развить навыки коллективной работы; 2) дать понятие направления в пространстве; 3) сформировать практические навыки определения направления в пространстве.
Урок-экскурсия "Геометрия вокруг нас". Урок можно провести, следуя потому же маршруту, который был использован на уроке 1, но теперь основное внимание сосредотачивается на форме окружающих предметов, среди которых дети стараются найти похожие, а также на поиске в объемных предметах знакомых плоскостных фигур (кругов, многоугольников разной формы и т.д.). (программный материал, не отраженный в учебнике).
Целью данного урока является ознакомление с понятием формы, и формирование абстрактного мышления – предметы в мире отличаются, но их форму можно свести к определенному набору фигур.
Задачи урока: 1) заинтересовать детей геометрией; 2) дать понятие формы предмета; 3) дать навыки определения форм и сравнения их между собой.
Урок-путешествие на тему "Зачем людям нужны числа". Урок проводится в окрестностях школы по маршруту, на котором ученики могут увидеть различные объекты, в которых использованы числа (номера домов, маршрутов автобусов и других видов транспорта, шкалы весов, цены товара и т.д.). При проведении урока желательно использовать стихотворение
Негаданно-нежданно
Нагрянула беда:
Все числа потерялись,
Исчезли без следа.
Как дом или квартиру
Без номера найти?
И к другу в день рожденья
Вовремя прийти?
Ведь стрелка не покажет
Нам время на часах,
И сколько весят фрукты,
Не видно на весах.
Отныне заблудиться.
Не стоит и труда:
Автобус без маршрута
Уходит в никуда.
Целью данного урока является ознакомление с понятием натурального числа, и формирование абстрактного мышления – предметы в мире отличаются, но их количество можно выразить через те же самые числа.
Задачи урока: 1) заинтересовать детей математикой; 2) дать понятие натурального числа; 3) дать навыки счета и сравнения чисел между собой.
Урок-экскурсия на тему "Линии вокруг нас". Урок желательно провести там же, где проходил урок 3, но сосредоточив внимание на поиске линий, как части рассматривавшихся на нем объемных и плоскостных объектов.
Целью данного урока является ознакомление с понятием линии, и формирование абстрактного мышления – предметы в мире отличаются, но их форму можно свести к определенному набору линий.
Задачи урока:
- заинтересовать детей геометрией;
- дать понятие линии;
- дать навыки определения линий и их направлений.
Урок-игра "Движемся по плану" (завершение работы над ориентацией в пространстве с использованием одного направления).
Целью данного урока является закрепление понятия направления, и формирование абстрактного мышления – все многообразие перемещений можно свести к определенному набору направлений.
Задачи урока:
- заинтересовать детей геометрией;
- закрепить представление об основных направлениях в пространстве;
- дать навыки определения направлений и движения по плану в пространстве.
На пришкольном участке или в любом выбранном для проведения урока помещения заранее устраиваются "тайники" с сюрпризами по числу команд, на которые учитель разделит учеников. Для каждой команды заготавливается план движения к одному из тайников с указанием поворотов и длины проходок по прямой между ними в шагах или с использованием любой другой мерки, которая вручается команде (это может быть палочка, кусок шнура и т.д.). Желательно, чтобы на каждом отрезке пути число мерок не превышало 9. Игра завершается, когда все команды найдут свой тайник. Те, кто справился с заданием раньше, могут по просьбе отставших оказывать им помощь. (Команды должны быть примерно равными по возможностям). [15;с.87]
2.2 Особенности использования дидактических игр в 1 классе
Для использования игр характерна общая структура учебного процесса, включающая четыре этапа:
1)Ориентация: учитель представляет тему, дает характеристику игры, общий обзор ее хода и правил.
2)Подготовка к проведению: ознакомление со сценарием, распределение ролей, подготовка к их исполнению, обеспечение процедур управления игрой.
3)Проведение игры: учитель следит за ходом игры, контролирует последовательность действий, оказывает необходимую помощь, фиксирует результаты.
4)Обсуждение игры: дается характеристика выполнения действий, их восприятия участниками, анализируются положительные и отрицательные стороны хода игры, возникшие трудности, обсуждаются возможные пути совершенствования игры, в том числе изменения правил.
При подборе и разработке игр нужно исходить из основных закономерностей обучения. Вот главная их них: обучение происходит только при активной деятельности учащихся. Чем разностороннее обеспечиваемая учителем интенсивность деятельности учащихся с предметом усвоения, тем выше будет качество на уровне, зависящем от характера организуемой деятельности – репродуктивной или творческой. Проведение игры требует мастерства от учителя. Перед игрой учитель должен доступно изложить ее сюжет, распределить роли, поставить перед детьми познавательную задачу, подготовить необходимое оборудование, сделать нужные записи на доске. В игре обязательно в той или иной роли должен участвовать каждый ученик класса. В системе уроков по теме важно подбирать игры на разные виды деятельности: исполнительную, воспроизводящую, контролирующую и поисковую. В игре следует продумывать не только характер деятельности детей, но и организационную сторону, характер управления игрой.
В процессе игр учитель должен постепенно воспитывать ведущих из числа лидеров, а в простых играх предлагать роль ведущего поочерёдно разным учащимся. [22;с.94]
Не следует приучать детей к тому, чтобы на каждом уроке они ждали новых игр или сказочных героев. Необходим последовательный переход от уроков, насыщенных игровыми ситуациями, к урокам, где игра является поощрением за работу на уроке или используется для активизации внимания: весёлые шутки-минутки, игры-путешествия в страну чисел или страну знаний.
Особенно широко используются игры на уроках при обучении детей шести-семилетнего возраста, поскольку ведущей деятельностью детей до поступления была игра, а с поступлением в школу происходит смена ведущей деятельности на учебную. Надо иметь в виду, что очень эффективными являются игровые формы обучения, различного рода дидактические игры. В этих условиях переход от одной ведущей деятельности к другой происходит безболезненно. Надо шире практиковать занимательные игровые формы обучения, которые вызывают большой интерес у детей (например, игру в магазин при обучении математике, обведение контуров рисунка при обучении письму, игру с куклами и мячами на уроках по развитию речи и т.д.)
Даже слаборазвитые, робкие и застенчивые дети охотно включаются в подобные игры. При этом надо чётко представлять себе, какую именно дидактическую нагрузку несёт содержание той или иной игры, и постепенно совершенствовать эту дидактическую основу. В ситуации весёлой, увлекательной дидактической игры дети более успешно усваивают знания, чем в процессе учебных занятий.
Разумеется, обучение нельзя превращать в сплошную игру. И в дальнейшем ученики, когда станут старше, поймут, что учение не игра, а труд, и труд серьёзный и ответственный, хотя по-прежнему радостный и увлекательный.
Младший школьник мыслит наглядно-образно, поэтому необходимо при применении дидактических игр использовать наглядность. Игра должна быть занимательной, интересной для детей, но ни в коем случае нельзя принудительно заставлять детей играть. Это не даст желаемого результата ни в развивающем, ни в образовательном плане.
В игре детям следует предоставлять большую самостоятельность, в то же время на них нельзя возлагать и большую ответственность. Важно, чтобы ребята сами следили за выполнением правил, чтобы каждый участник игры чувствовал ответственность перед коллективом.
Дидактические игры кратковременны (10-20 мин.), и важно, чтобы всё это время не снижалась умственная активность играющих, не падал интерес к поставленной задаче. Особенно важно следить за этим в коллективных играх. Нельзя допустить. чтобы решением задачи был занят один ребёнок, а другие бездействовали. Обычно при таком проведении игры дети быстро утомляются от пассивного ожидания. Другая картина наблюдается, если все играющие включены в решение задачи. [13;с.56]
В игре проявляются особенности характера ребёнка, обнаруживается уровень его развития. Поэтому игра требует индивидуального подхода к детям. Учитель должен считаться с индивидуальными особенностями каждого ребёнка при выборе задания, постановке вопроса: одному дать задание надо легче, другому – труднее, одному стоит задать наводящий вопрос, а от другого потребовать вполне самостоятельного решения. Особого внимания требуют дети робкие, застенчивые: иногда такой ребёнок знает правильный ответ, но от робости не решается ответить, смущенно молчит. Учитель помогает ему преодолеть застенчивость, одобряет его, хвалит за малейшую удачу, старается чаще его вызывать, чтобы приучить выступать перед классом (коллективом).
Дидактические игры особенно необходимы в воспитании и обучении детей шестилетнего возраста. В них удаётся сконцентрировать внешне даже самых инертных детей. В начале дети проявляют интерес только к игре, а затем и к тому учебному материалу, без которого участие в игре невозможно. Как показывают наблюдения за детьми шестилетнего возраста, наибольших успехов достигают те учителя, которые отводят на игру третью часть урока. Недооценка или переоценка игры отрицательно сказывается на учебно-воспитательном процессе. При недостаточном использовании игры снижается активность учащихся на уроке, ослабляется интерес к обучению, при её чрезмерном использовании ученики с трудом переключаются на обучение в неигровых условиях.
В работе при обучении учащихся, большое внимание необходимо уделять нестандартным задачам на построение цепочки логических рассуждений. Решение таких задач учащиеся легко отыскивают с помощью составление таблицы или схемы. Приведу пример такой задачи, которую можно предложить ученикам 1 класса: «Игорь грустнее Жени, Женя грустнее Севы. Нарисуй лица мальчиков».
Вот еще несколько заданий на развитие логического мышления: «Ошибки-невидимки».
На доске записано несколько математических выражений, содержащих явную ошибку. Задача учащихся, ничего не стирая и не зачеркивая, сделать ошибку «невидимой».
Возможные варианты выполнения задания учащимися:
20<20 6=5
а) 20<200 а) 6=5+1
б) 20<20+8 б) 11 – 6 =5
Представленные задания вызывают у детей большой интерес. А ведь именно интерес должен лежать в основе обучения младшего школьника.
При изучении темы «Сложение и вычитание в пределах 10» использовались нижеперечисленные игры. При этом учебный процесс осуществлялся в соответствии со следующими этапами: ознакомление, повторение, закрепление изученного материала. Приведем конспекты нескольких уроков с использованием этих игр.
Тема урока: «Перестановка слагаемых»
Цель урока: Познакомить детей с переместительным свойством сложения.
Ход урока
Организационный момент
Прозвенел звонок веселый.
Всех зовет он на урок.
Ну-ка, дети, все готовы?
Начинаем точно в срок.
На места все тихо сядем,
Не нарушим тишину.
Приготовились все слушать,
Я урок сейчас начну.
2. Повторение изученного.
У. Послушайте внимательно тексты загадок-обманок, сочиненных современным детским поэтом Марком Шварцем. Отгадайте, кто пришел сегодня к нам на урок.
Клубком свернулся – ну-ка тронь!
Со всех сторон колючий… (Еж.)
- Ребята, ежик просит вас сосчитать от 1 до 10 через одно и два числа.
Дети выполняют задание.
Кто в малине знает толк?
Косолапый, бурый… (Медведь)
- Ребята, косолапый мишка тоже хочет дать вам задание. Выполним его?
Д. Да
У. Сосчитайте от 10 до 1 через одно и два числа.
Дети выполняют задание.
У. На заборе поутру
Кукарекал… (Петух.)
- Петушок приготовил вам задание посложнее. Сосчитайте от 1 до 20 и от 20 до 1.
Дети выполняют задание.
Кто любит по ветвям носиться?
Конечно, рыжая… (Белка.)
- Ребята, белочка приготовила для вас игру, которая называется: «Считай верно»
Цель игры: формирование навыка табличного сложения и вычитания в пределах 10 и умения пользоваться терминами «слагаемое», «сумма».
Оборудование: у учащихся карточки с числами от 0 до 9.
Описание игры: перед каждым учеником разложены в любом порядке лицевой стороной вверх карточки с числами от 0 до 9. Учитель читает выражение. Ученики, решив его, ищут карточку с ответом и переворачивают ее лицевой стороной вниз. Учитель дает 6-7 примеров с различными ответами.
- Найди сумму чисел 5 и 4.
- На сколько 6 больше 3?
- К 4 прибавь столько же.
- Увеличь 3 на 4.
- Первое слагаемое равно 2, второе – 3. Чему равна сумма?
- 5 плюс 1.
- А теперь проведем проверку. Те, у кого остались не перевернутыми карточки с числами 0,1,2 и 4 правильно справились с заданием.
У. Молодцы ребята, вы выполнили задания героев загадок.
2. Изучение нового материала.
У. - Все преграды одолев,
Бьет копытом верный… (Конь.)
- В цирковом представлении первым номеров выступали 5 лошадей.
На наборное полотно выставляются 5 предметных картинок с изображением лошадей.
- Сено хоботом берет
Толстокожий … (Слон.)
- После лошадей на арену цирка вышли 3 слона.
На наборное полотно выставляются 3 предметные картинки с изображением слонов.
- Как узнать, сколько всего лошадей и слонов участвовало в цирковом представлении?
Д. 5+3=8
У. В следующем представлении участвовали сначала слоны, а затем лошади. Как узнать, сколько слонов и лошадей участвовало в цирковом представлении?
Д. 3+5=8
У. Как одним словом назвать данные записи?
Д. Равенства.
У. Сравните равенства: чем они похожи, чем отличаются.
Д. Одинаковые слагаемые и сумма. Слагаемые поменяли местами.
3. Усвоение нового материала
4. Физкультминутка
Ветер дует нам в лицо,
Закачалось деревцо.
Ветер тише, тише, тише,
Деревцо все выше, выше, выше.
5. Повторение изученного.
6. Итог урока.
У. Что вы сегодня узнали нового. Что смогли для себя открыть?
  Тема урока: «Решение примеров вида 6- , 7- » Тема урока: «Решение примеров вида 6- , 7- »
Цель урока: Познакомить с приемом вычитания из чисел 6 и 7 на основе взаимосвязи сложения и вычитания.
Ход урока
1. Организационный момент.
2. Повторение изученного.
Прежде чем приступить к изучению новой темы, мы повторим пройденный материал, состав чисел 6 и 7.
- Посмотрите на «волшебное колесо» и подумайте, по какому правилу в нем расположены числа. (Сумма чисел, расположенных на любой прямой линии равна 8)
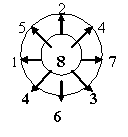
- Расположите числа в « волшебном колесе» так, чтобы сумма чисел, расположенных по любой прямой линии в первом колесе была равна 6, а во втором – 7.
 
       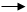 6 7 6 7
3. Изучение нового материала
– Молодцы, с этим заданием вы справились и теперь можем приступить к изучению новой темы (проводится практическая работа),
4. Усвоение нового материала
- А теперь я предлагаю вам поиграть в игру «Угадайка»
5. Повторение пройденного материала
Для формирования навыка сложения и вычитания в пределах 10 детям была предложена игра «Математическая эстафета».
Дидактическая цель: закрепление приемов прибавления и вычитания в пределах 10.
Оборудование: рисунки цепочек на доске:

Содержание игры:
- Ваша задача по одному от каждого ряда выйти к доске, выполнить указанные действия, заполнить пустые круги и передать эстафету (мел) следующему ученику из своей команды. Выигрывает та команда, которая не допустит ни одной ошибки и первой правильно закончит выполнение цепочки.
- Молодцы, каждая команда выполнила задание правильно, в этом вам помогло знание таблицы сложения и вычитания в пределах10.
6. Итог урока
- Вам понравился урок? Чем? Что нового вы открыли для себя?
Кроме таких уроков проводились уроки-путешествия. В уроках-путешествиях ненавязчиво закрепляется изученный материал, обогащается словарный запас, активизируется внимание детей, расширяется кругозор, прививается интерес к предмету, развивается творческая фантазия и воспитываются нравственные качества. И главное - ни одного скучающего на уроке. Всем интересно, дети играют, а играя, непроизвольно закрепляют и доводят до автоматизированного навыка математические знания. Приводим конспекты таких уроков.
Тема урока: «Сложение и вычитание 1, 2» (закрепление)
Цели урока: Закрепить знание случаев сложения, вычитания с 1, 2.
Ход урока
1. Организационный момент.
2. Тема урока.
Учитель. Сегодня мы отправляемся в гости к героям разных сказок. Они хотят посмотреть, чему вы научились – умеете ли вы решать примеры, задачи. А как надо вести себя в гостях?
Дети. Громко не разговаривать, уважительно относиться к хозяевам…
У. Ребята, мы пойдем по сказочной улице, где в своих сказочных домиках живут герои мультфильмов. Отгадав загадку, вы узнаете, к кому первому мы отправляемся в гости.
Не артист, а голосист.
Не ездок, а шпоры у ног.
Кто это?
Д. Петушок!
У. Как вы думаете, в каком домике живет Петушок?
Д. В доме номер 1.
У. Петушок предлагает вам следующие вопросы и задания.
На доске прикреплен рисунок: петушок держит в клюве конверт с заданиями.
Задания.
1. Посчитайте до 10 в прямом и обратном порядке.
2. Игра «Молчанка».
Дидактическая цель:
формирование навыков сложения и вычитания 1,2.
Примеры даны на карточках:
1+1 2+2 3+1
5+1 6-2 8-1
9-1 4+2 9-2
Дети работают с кассой, показывают ответы.
У. А теперь, когда мы решили примеры, зашифрованные на листочке, продолжим игру так: Я буду задавать вопрос, а вы показывать ответ.
Какое число следует за числом 7?
Какое число стоит перед 6?
Какое число больше 3 на 2?
Какое число меньше 8 на 2?
Дети отвечают
- Давайте скажем Петушку спасибо, попрощаемся с ним и отправимся в гости к девочке, рост которой не больше дюйма. Догадались, кто это?
Д. Дюймовочка.
У. Правильно. Дюймовочка живет в доме номер 9. Мимо домов с какими номерами мы пойдем, если будем двигаться только по правой стороне улицы?
Д. Мимо домов с номерами 1, 3, 5, 7.
У. Дюймовочка предлагает вам решить пример 6+2 разными способами.
Д. К 6 прибавить 2; к 6 прибавить 1 и еще 1.
У. Какое действие мы должны выполнить, чтобы получить ответ?
Д. Сложение.
У. Назовите число, которое больше 6 на 2. Составьте с этими же числами пример на вычитание.
Д. 8-2=6
У. Скажем Дюймовочке до свидания и отправимся в домик под номером 4, где живет Баба Яга. Что нам надо сделать, чтобы найти этот домик?
Д. Перейти через дорогу.
У. А как вы будете переходить через дорогу?
Д. По пешеходному переходу. Сначала посмотрим налево, а на середине дороги – направо.
У. Баба Яга приготовила вам трудные задания. Она просит сравнить числа 8 и 5, 4 и 6.И спрашивает, почему 8 больше 5.
Д. Потому что в натуральном ряду чисел 8 стоит правее 5.
У. Почему 4 меньше 6?
Д. Потому что в натуральном ряду чисел стоит левее 6.
У. Кто знает, откуда появилась запись числа? Вам трудно ответить на вопрос, поэтому я расскажу эту историю.
    Давным-давно числа записывались по-другому. В Египте, например, числа первого десятка обозначались количеством палочек: так число 3 - и т.д. Давным-давно числа записывались по-другому. В Египте, например, числа первого десятка обозначались количеством палочек: так число 3 - и т.д.
Греки и славяне цифры обозначали буквами, но, чтобы не путать их с обычными буквами, над ними ставили знак –
Десятичная запись числа была изобретена в Индии, потом ее переняли арабы, и от арабов она уже перешла к нам. Поэтому мы называем наши цифры арабскими.
- А теперь пойдем в гости в домик номер 2. Жалко, что дома никого нет, но нам оставили записку с заданием.
У детей на партах карточки с заданием: Соедини точки по порядку.

У. Соединив точки, мы получили рисунок. Что на нем изображено?
Д. Кусочек сыра.
У. Как вы думаете, кто мог погрызть сыр?
Д. Мышки.
У. Теперь вы знаете, кто живет в этом домике. Они предлагают вам такое задание: составьте задачу по картинке.
Д. На ветке сидели две белки, потом к ним прыгнула еще одна белка. Сколько всего стало белок на ветке?
У. Давайте вспомним, из каких частей состоит задача.
Д. Условие и вопрос.
У. Назовите условие этой задачи.
Д. На ветке сидели две белки, к ним прыгнула еще одна белка.
У. Каков вопрос к задаче?
Д. Сколько всего белок стало на ветке?
У. Какое решение этой задачи?
Д. К 2 прибавить 1 получится 3.
У. А что такое 3?
Д. Это ответ.
У. Составьте две обратные задачи.
Ответы детей.
3. Физкультминутка
Вышли мышки как-то раз
Посмотреть который час.
Раз, два, три, четыре –
Мышки дернули за гири.
Тут раздался страшный звон.
Побежали мышки вон.
4. Тема урока (продолжение)
У. Теперь отправляемся в домик номер 3.
А кто же там живет? Мы узнаем
это, если вспомним слова:
Я от дедушки ушел,
Я от бабушки ушел,
У меня румяный бок,
А зовусь я …
Д. Колобок.
У. Колобок выполняет домашнее задание, но никак не может справиться с одним заданием. Давайте поможем Колобку!
5+1 5+2
9-1-1 8-1-1
У. Ребята, решив примеры за Колобка, правильно ли мы поступили?
Д. Нет.
У. Почему? Что надо было сделать?
Д. Объяснить Колобку решение.
Дети объясняют ход решения примеров.
У. Идем дальше, в домик номер 10. Здесь живет лиса. Она приготовила вам «хитрые» задания.
Перед детьми карточки, на которых изображены человечки, составленные из геометрических фигур.
- Какие геометрические фигуры вы видите?
Д. Треугольник, овал, круг …
У. До домика с каким номером мы дошли?
Д. До домика номер 10.
У. Ой, смотрите, тяжелые черные тучи закрыли солнышко, и сейчас пойдет дождь. Давайте вернемся в домик номер 2 и попросим у мышек зонтики. Мимо домов, с какими номерами мы будем бежать?
Д. Мимо домов с номерами 8,6,4.
У. Вот мы и добежали до дома номер 2 (каждый ученик получает зонтик). Но зонтики, к сожалению, белые. Давайте, чтобы они были красивыми, их раскрасим. Но сначала надо решить примеры: 3+2; 9-1; 8-2;, а затем сектор с ответом 5 раскрасим зеленым цветом , 6 –желтым, 8- красным.
Дети выполняют задания. Проводится фронтальная проверка.
У. Поднимите зонтики над головами, чтобы вас не замочил дождь.
5. Итог урока
Оценка работы детей на уроке. Дети в качестве поощрения получают фигурки сказочных героев.
Тема урока: « Сложение и вычитание чисел 5,6,7,8,9 (закрепление)»
Цели урока: Повторение знание состава чисел, компонентов при сложении; закрепить умение применять приемы прибавления и вычитания чисел в пределах 10.
Ход урока
Организационный момент
Учитель. Сегодня наш урок будет необычным и занимательным. Сегодня к нам на урок придет сказка и поможет нам лучше узнать математику. Мы отправимся в путешествие по сказкам на ковре-самолете в сказочное Математическое королевство. Для этого мы должны сказать волшебные слова: крабле-крибли-бумс.
Звучит музыка, открывается доска
2. Новый материал
У. Перед вами сказочное Математическое королевство. Правит этим королевством мудрый король. Он издал указ: « Повелеваю ребятам выполнять все мои желания!» Первое желание короля узнать, внимательны ли вы. Вот его задания.
Задания.
1. Росли две вербы. На каждой вербе по 2 ветки, на каждой ветке по 2 груши. Сколько всего груш?
2. На яблоне было 10 яблок, а на иве на 2 меньше. Сколько всего было яблок?
3. Крышка стола имеет четыре угла. Один угол отпилили. Сколько стало углов у крышки стола? - Итак, вы справились с заданием, и король разрешил вам путешествовать по его королевству. Смотрите, наш ковер-самолет пролетает над лесом. Кто же это идет по тропинке? Дети. Винни-Пух и Пяточок.
У. Из какой они сказки?
Д. Из сказки « Винни-Пух и все- все- все».
У. А куда они идут? Д. В гости к Кролику.
У. Но почему он их не угощает? Ах, вот в чем дело. Оказывается, у него закончился пирог. Чтобы его купить, нужно сходить к Сове. Но она продаст пирог, если Пятачок и Винни-Пух выполнят все задания. Давайте, ребята, мы им поможем.
Д. Да.
У. Вставьте пропущенный знак и число.
Ответы детей
- Какое число можно вставить в «окошечко»?
3+2>
Ответы детей
- С числами 2, 3, 4 составьте все возможные примеры на сложение, используя их в качестве слагаемых.
Дети выполняют задание.
У. А теперь игра « День и ночь». Когда я скажу «ночь», вы закрываете глаза и начинаете считать. Когда я говорю «день», то вы открываете глаза и называете ответ.
3+1+2-4+5+1-4+6
6+3-7+6+2-5+4-8
Ответы детей
У. Молодцы! Вы помогли выполнить задания Винни-Пуху и Пятачку. Сова им продаст пирог, и они буду пить с ним чай.
Наше путешествие продолжается. Мы летим над синим морем. « А у самого синего моря жил старик со своею старухой». Какая это сказка?
Д. «Сказка о рыбаке и рыбке».
У. Кто автор?
Д. Александр Сергеевич Пушкин.
У. Вот мы в гостях у золотой рыбки. Она приплыла к нам не одна, а со своими подружками и предложила поиграть в игру « Математическая рыбалка».
- Кто из рыбаков поймал больше рыбок?
У. Раскрасьте курточку каждого рыбака и рыбок, которых он поймал, одинаковым цветом.
Дети выполняют задание
У. Что же мы будем делать с пойманными рыбками?
Д. Отпустим их в синее море, пусть гуляют себе на просторе.
У. Снова в путь. Наш ковер-самолет пролетает над красивым домом, в котором живет Мальвина. На лужайке сидит мальчик и горько плачет. Ребята, как зовут этого мальчика.
Д. Буратино.
У. Правильно. А из какой он сказки?
Д. Из сказки Алексея Николаевича Толстого « Приключения Буратино».
У. Сейчас мы узнаем, почему он плачет. Оказывается, Буратино не может решить задачи, которые ему задала Мальвина. Ребята, давайте поможем.
Учитель читает задачу вслух.
1. В ведре 9 л воды, а в кастрюле – 4 л. Где воды больше? Почему? На сколько больше? Как это узнать?
Масса судака 3 кг, а трески – 1 кг. Какая рыба тяжелее?
3. У Вити решено 6 примеров, он еще должен решить 4. Сколько примеров у него будет решено?
4. На одной полке 9 книг, а на другой – на 4 книги меньше. Сколько книг на другой полке?
У. Вы очень хорошо и быстро решили задачи. Но нас ждут и другие испытания.
3. Физкультминутка
На одной ноге постой - ка,
Будто ты солдатик стойкий.
Ногу левую - к груди.
Да смотри - не упади.
А теперь постой на левой,
Если ты солдатик смелый.
У. Ребята, в какой сказке живет смелый стойкий солдатик?
Д. В сказке Ганса Христиана Андерсена « Стойкий оловянный солдатик».
У. А сейчас мы полетим в гости к Незнайке. Он давно нас ждет. Мы ему должны помочь найти ошибки.
1 вариант 2 вариант
8-2=5 4+6=9 6+3=10 7-2=5
5+4=10 7-3=4 9- 4=6 4+5=10
2+8=9 9-5=5 3+7=8 9-3=5
Звучит запись песни В. Шаинского « Чебурашка».
У. Послушайте, ребята, кто же поет эту песню?
Д. Это Чебурашка.
У. Правильно. Назовите имя его друга.
Д. Крокодил Гена.
У. Верно. Чебурашка и Крокодил Гена приготовили для вас задание. Вам нужно расшифровать слова.
| У |
2+8 |
Ж |
9-3 |
| Р |
2+6 |
Б |
8-5 |
| А |
6-4 |
Д |
5+4 |
  9 9 |
8 |
10 |
6 |
3 |
2 |
5. Итог урока.
У. Ребята, а какое слово было зашифровано?
Д. Это слово «дружба».
У. Нравится вам это слово?
Д. Да.
У. Почему? Какими должны быть друзья? Как вы понимаете пословицу
« Друзья познаются в беде». Назовите героев сказок, которым мы пришли на помощь?
Ответы детей.
- Наше путешествие подошло к концу. Сказка прощается с вами. Чему учили нас сказочные герои?
2.3 Опытно-экспериментальная работа
Прежде чем подбирать упражнения и всевозможные игры для использования на уроках, мы выявили, какие знания лежат в основе сложения и вычитания в пределах 10.
последовательность чисел в отрезке от 1 до 10
нумерация
смысл числа
отношения «больше», «меньше»
состав числа
Все эти знания необходимы для сознательного и прочного усвоения материала. Поэтому первым нашим шагом было выяснение того, насколько этими знаниями и соответствующими умениями владеют учащиеся. Для этого была проведена самостоятельная работа, которая дала возможность определить имеющийся у учащихся уровень знаний по данным вопросам.
В самостоятельной работе были даны следующие задания:
Какие числа пропущены?
Запиши цифрой: сколько кругов нужно дорисовать.
Сравни количество предметов на картинках. Запиши неравенства.
Самостоятельная работа проводилась в 1 классе «А» (контрольном) и 1 классе «Б» (экспериментальном) в Кукморской средней школе №2:
1 класс «А» (контрольный) - 19 человек
1 класс «Б» (экспериментальный) – 20 человек
Результаты самостоятельной работы были занесены в таблицу 1.
Таблица 1
| 1 «А» класс контрольный |
1 «Б» класс эксперементальный |
| Писали работу |
19чел. |
20чел. |
| Выполнили верно |
12чел.(63,1%) |
12чел.(60%) |
| Допустили ошибки на нумерацию чисел в пределах 10 |
1чел.(5,2%) |
- |
| Допустили ошибки на состав числа |
7чел.(36,8%) |
7чел.(35%) |
| Допустили ошибки на сравнение чисел |
4чел.(21%) |
4чел.(20%) |
Анализ детских работ показал, что на начало эксперимента уровень знаний у детей контрольного и экспериментального классов находится на одном уровне.
Проведенный анализ позволил спланировать дальнейшую работу. В экспериментальном классе мы учли, что некоторые учащиеся не совсем хорошо усвоили необходимый материал. Поэтому в начале каждого урока давались задания на активизацию ранее приобретенных знаний.
В 1 классе «Б» (экспериментальном) на уроках математики вводились дидактические игры. Они были направлены:
- на подготовку к изучению нового материала;
- на изучение нового материала;
- на закрепления изученного материала.
Игры давались систематически, в соответствии с целями и задачами урока. Дети охотно включались в дидактическую игру, с охотой принимали ее условия. Здесь даже пассивные, несмелые дети активно включались в работу, применяя на практике свои знания и умения. Особенно учащимся нравились задания, в которых надо исправить ошибки. От них требовалось не только исправить ошибки, но и объяснить, почему допущена ошибка. Отобранные дидактические игры позволили повысить активность учащихся в их деятельности, ведь ребенок сам активно участвует в процессе познания, сам решает какие знания и умения ему потребуются для выполнения поставленной задачи.
В уроки так же включались сюжеты знакомых детям сказок и герои литературных произведений. Мы старались объединить уроки одной темой, одной сюжетной игрой. Так, например, при проведении урока-игры, дети отправились путешествовать в Математическое Королевство. По пути дети делали остановки, во время которых не только повторяли изученный материал, но и вспоминали литературные произведения, с их героями, вспомнили о дружбе, о друзьях, которым надо помогать, в игре-путешествии дети расширяли свой кругозор.
Отобранные игры давались на каждом уроке, естественно, форма подачи, виды и время игры или задания менялись в зависимости от цели и задачи урока.
В конце 1 полугодия в контрольном и экспериментальном классах была проведена еще одна самостоятельная работа.
Найди значения выражений:
4+4 3+7 10-2 7-5
3+5 5+4 8-3 9-2
6+2 2+7 6-4 5-3
8+1 4+3 3-3 8-6
Результаты этой работы были занесены в таблицу 2.
Таблица 2
| 1 «А» класс контрольный |
1 «Б» класс эксперементальный |
| Писали работу |
19чел. |
20чел. |
| Выполнили верно |
10чел.(52,6%) |
14чел.(70%) |
| Допустили ошибки на сложение |
4чел.(21%) |
2чел.(10%) |
| Допустили ошибки на вычитание |
7чел.(36,8%) |
4чел.(20%) |
В самостоятельной работе надо было найти значения выражений за ограниченный промежуток времени (10минут).
Результаты этой работы показывают, что в экспериментальном классе дети лучше усвоили материал, выполнили работу быстрее, допустив меньше ошибок при решении.
Далее в экспериментальном классе была продолжена работа с использованием на уроках дидактических игр, по итогам которой, была проведена итоговая работа.
Найди значения выражений:
10-9 2+7 9-5 3+6
8-5 6-6 1+3 8-7
8+2 4+6 9-0 10-6
9+1 7-3 2+6 4+3
Результаты были проанализированы и занесены в таблицу 3.
Таблица 3
| 1 «А» класс контрольный |
1 «Б» класс эксперементальный |
| Писали работу |
19чел. |
20чел. |
| Выполнили верно |
9чел.(47,4%) |
17чел.(85%) |
| Допустили ошибки на сложение |
8чел.(42,1%) |
2чел.(10%) |
| Допустили ошибки на вычитание |
6чел.(31,5%) |
2чел.(10%) |
Сопоставительный анализ уровня знаний учащихся в контрольном и экспериментальном классах показал, что учащиеся экспериментального класса лучше справились с работой. В экспериметальном классе 17 человек выполнили работу верно, а в контрольном классе - 9 человек. Допустили ошибки на вычитание в экспериментальном классе 2 человека, а в контрольном -6 человек. Мы убедились, что игровая деятельность способствует не только активизации познавательной деятельности, но и формированию умения безошибочно вычислять.
Применение дидактических игр позволило сделать обучение младших школьников более интересным, занимательным, активизировать мыслительную деятельность и воображение, повысить уровень внимания и памяти. Использование дидактических игр стимулирует активность каждого ребенка, повышает качество процесса обучения младших школьников.
2.4 Вывод по 2-ой главе
В период обучения большое место в жизни и обучении занимают игры. В них ребенок учится подчинять свое поведение правилам, формируется внимание, умение сосредоточиться. То есть развиваются личностные качества и способности ребенка, которые важны для успешного обучения.
Чтобы сформировать у младших школьников умение складывать и вычитать числа в пределах 10 необходимо целенаправленная активизация их учебной деятельности. Способом такой активизации является дидактическая игра. Подбор игр должен осуществляться с учетом возрастных особенностей детей, уровнем их подготовленности и в соответствии с целями и задачами урока. Игры можно использовать на разных этапах урока, эффективны уроки-путешествия. Выделяют также условия формирования познавательного интереса, а именно: максимальная опора на активную мыслительную деятельность учащихся, ведение учебного процесса на оптимальном уровне развития учащихся, положительный эмоциональный тонус учебного процесса, благоприятное общение в учебном процессе.
Познавательный интерес к математике формируется и развивается в процессе учения. Главная цель учителя заключается в том, чтобы заинтересовать учащихся своим предметом. А успешно осуществлять данную цель можно не только на уроках, но и во внеклассной работе по математике.
В основе любой игровой методики, проводимой на занятиях и внеклассных мероприятиях, должны лежать следующие принципы:
- актуальность дидактического материала;
- коллективность;
- соревновательность.
Заключение
В результате проведенного исследования согласно поставленным задачам было подтверждено, что в педагогической работе большое внимание следует уделять дидактической игре на уроке. Дидактическая игра содействует лучшему пониманию математической сущности вопроса, уточнению и формированию математических знаний учащихся. Игры можно использовать на разных этапах усвоения знаний: на этапах объяснения нового материала, его закрепления, повторения, контроля. Игра позволяет включить в активную познавательную деятельность большее число учащихся. Она должна в полной мере решать как образовательные задачи урока, так и задачи активизации познавательной деятельности, и быть основной ступенью в развитии познавательных интересов учащихся. Игра помогает учителю донести до учащихся трудный материал в доступной форме. Отсюда можно сделать вывод о том, что использование игры необходимо при обучении детей младшего школьного возраста.
Методики, использованные учителем на практике, хорошо зарекомендовали себя даже при кратковременном применении (порядка 2-х недель). Есть основание полагать, что при постоянном их использовании на этапе повторения знаний, и в учебно-воспитательном процессе вообще, эти методики будут иметь еще большую эффективность, формируя устойчивый интерес учащихся к изучаемой теме и учебному процессу в целом.
Итак, мы рассмотрели в данной дипломной работе историко-педагогический аспект проблемы формирования познавательного интереса в процессе обучения; понятие «познавательный интерес», его структура; взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике; дидактические игры, их виды; особенности использования дидактических игр в 1 классе; провели опытно-экспериментальную работу с 1«А» и 1«Б» классами. Рассмотрели примеры использования дидактических игр на уроках математики, проведенных в Кукморской средней школе №2. В связи с этим можно сделать следующие выводы:
Познавательный интерес психологи и педагоги изучают с разных сторон, но любое исследование рассматривает интерес как часть общей проблемы воспитания и развития.
Познавательный интерес – это избирательная направленность личности на предметы и явления окружающей действительности.
Познавательный интерес можно рассматривать с разных сторон: как мотив учения, как устойчивую черту личности, как сильное средство обучения. Для того чтобы активизировать учебную деятельность школьника нужно систематически возбуждать, развивать и укреплять познавательный интерес и как мотив, и как стойкую черту личности, и как мощное средство обучения.
Структура. Существует четыре уровня развития познавательного интереса. Это любознательность, любопытство, познавательный интерес и теоретический интерес. Учителю нужно уметь определять, на какой стадии развития познавательный интерес у отдельных учащихся, для того чтобы способствовать укреплению интереса к предмету и его дальнейшему росту.
Существует определенная взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике.
Чтобы сформировать у младших школьников умение складывать и вычитать числа в пределах 10 необходимо целенаправленная активизация их учебной деятельности. Способом такой активизации является дидактическая игра. Подбор игр должен осуществляться с учетом возрастных особенностей детей, уровнем их подготовленности и в соответствии с целями и задачами урока. Игры можно использовать на разных этапах урока, эффективны уроки-путешествия. Выделяют также условия формирования познавательного интереса, а именно: максимальная опора на активную мыслительную деятельность учащихся, ведение учебного процесса на оптимальном уровне развития учащихся, положительный эмоциональный тонус учебного процесса, благоприятное общение в учебном процессе.
Познавательный интерес к математике формируется и развивается в процессе учения. Главная цель учителя заключается в том, чтобы заинтересовать учащихся своим предметом. А успешно осуществлять данную цель можно не только на уроках, но и во внеклассной работе по математике.
В основе любой игровой методики, проводимой на занятиях и внеклассных мероприятиях, должны лежать следующие принципы:
- актуальность дидактического материала;
- коллективность;
- соревновательность.
Мы рекомендуем использовать дидактические игры учителям начальных классов общеобразовательных школ.
Также рекомендуем литературу, использованную нами при проведении данной работы и указанную в списке литературы.
Список использованной литературы
1. Бантова М. А., Бельтюкова Г. В., Степанова С. В. Методическое пособие к учебнику «Математика. I класс»: Пособие для учителя. - М.: Просвещение, 2003.
2. Бахир В.К. Развивающее обучение // Начальная школа. - 2004.-№ 5.-С.26-30.
3. Букатов В.М. Педагогические таинства дидактических игр: Учебно-методическое пособие / В.М. Букатов. - М.: Московский психолого-социальный институт: Флинта, 2005.
4. Вайс В. Перспективное планирование воспитательной работы в начальной школе // Воспитание школьников. - 2005.
5. Вайндорф-Сысоева М.Е., Крившенко Л.П. Педагогика: Краткий курс лекций. - М.: Юрайт-Издат, 2004.
6. Гаврилычева Г.Ф. Развитие самостоятельности у детей // Нач. шк.,2005, №11.
7. Горенков Е.М. Технологические особенности совместной деятельности учителя и учащихся в дидактической системе Л.В. Занкова // Начальная школа. - 2004. - № 2. - С. 57-62.
8. Далингер В.А., Самостоятельная деятельность учащихся – основа развивающего обучения. // Математика в школе, №6, 2004.
9. Демидова С.И., Денищева Л.О. Самостоятельность учащихся при обучении математике. - М.: Просвещение, 2005
10. Дрозд В.Л., Урбан М.А. От маленьких проблем - к большим открытиям // Начальная школа. - 2005. - № 5. - С.37.
11. Еженедельная учебно-методическая газета “Математика” №21, 2003
12. Еженедельная учебно-методическая газета “Математика” №22, 2004
13. Жарова А.В. Учить самостоятельности.-М.,2005.
14. Ивашова О.А. Роль исследовательской деятельности младших школьников в овладении математической культурой //Сборник научных трудов по непрерывному образованию. Выпуск. 4. «Метаметодика: продуктивный диалог предметных методик обучения» - СПб.: «Культ-Информ-Пресс», 2003.
15. Истомина Н.Б. Методика обучения математике в начальной школе: Учеб. пособие для студ. сред. и высш. пед. учеб. завед. - М.: «Академия», 2004
16. Ксензова Г.Ю. Перспективные школьные технологии: Учебно-методическое пособие. - М.: Педагогическое общество России, 2005.
17. Кошмина И.В. Межпредметные связи в начальной школе. - М.: Гуманит. изд. центр ВЛАДОС, 2004.
18. Коджаспирова Г.М., Коджаспиров А.Ю. Педагогический словарь: Для студентов высших и средних педагогических заведений – М. – Издат. центр «Академия», 2005. – 176с.
19. Кульбякина Л.Я., Зотова Т.Н. Вопросы в методике преподавания математике // Начальная школа. - 2004.
20. Левитас Г.Г. Решение текстовых задач с помощью уравнений // Начальная школа. - 2005
21. Математика для II класса начальной школы. В 2 ч. / М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. - М.: Просвещение, 2006.
22. Михайлова Ф.Р. Памятки - способ самоорганизации учебной деятельности младших школьников // Интернет-журнал "Эйдос". - 2005.
23. Метельский И.В. Как поставить перед учащимися учебную задачу // Начальная школа. - 2004.
24. Педагогический энциклопедический словарь/Гл. ред. Б.М. Бим-Бад; Редкол.: М.М. Безруких, В.А. Болотов, Л.С. Глобова и др. – М.: Большая Российская Энциклопедия, 2006. – 528.:ил.
25. Подласый И.П. Педагогика. Новый курс: учебник для студентов педагогических вузов: в 2 КН. – м.: Гуманит. Издат. Центр ВЛАДОС, 2005.
26. Попова А.И., Литвинская И.Г. Развитие самодеятельности младших школьников в условиях коллективных занятий// Нач.шк.,№7,2004.
27. Программы образовательных учреждений. Начальные классы. В 2 ч. Ч. 1. Математика / М. И. Моро, Ю. М. Колягин, М. А. Бантова, Г. В. Бельтюкова и др. - М.: Просвещение, 2005.
28. Педагогика: учебник для студентов педагогических вузов и педагогических колледжей/Под ред. П.И. Пидкасистый. М.: Пед. Общ. России, 2004.
29. Педагогика: Учебное пособие для студентов педагогических учебных заведений, В.А. Сластенин, И.Ф.Исаев, А.И.Мищенко, Е.Н.Шиянов. – 4-е изд. – М.: Школьная Пресса, 2005.
30. Развитие исследовательских умений учащихся общеобразовательной школы: методический аспект. Круглый стол //Вестник Северо-западного отделения Российской Академии Образования. Образование и культура Северо-запада России. Выпуск 7. Тенденции в развитии и модернизации современного образования СПб, 2004.
31. Реан А.А., Бордовская Н.В., Розум С.И. Психология и педагогика. – СПб.: Питер, 2003.
32. Столяренко Л.Д. Педагогика. Серия «Учебники, учебные пособия». Ростов н/Д; «Феникс», 2005. – 448с.
33. Смолеусова Т.В. Этапы, методы и способы решения задач // Начальная школа. -2003. - №12. -С.62-66.
34. Темербекова А.А. Методика преподавания математики: Учеб. пособие для студ. вузов. - М.: Гуманит. изд. центр ВЛАДОС, 2004.
35. Татьянченко Д., Воровщиков С. Развитие общеучебных умений школьников. //Народное образование №8, 2003
36. Чиверская Л.Н, Формирование мыслительных операций у младших школьников на уроках математики.- Ульяновск, УИПК ПРО,2006
37. Царева С.Е. Нестандартные виды работы с задачами на уроке как средство реализации современных педагогических концепций и технологий // Начальная школа. - 2004.
38. Цукарь А.Я. Элементы исследовательской деятельности младших школьников на уроках математики // Начальная школа. - 2005.
39. Щукина, Г.И. Активизация познавательной деятельности учащихся в учебной деятельности. - М: Просвещение, 2004.
40. Щукина, Г.И. Педагогические проблемы формирования познавательного интереса учащихся. - М: Просвещение, 2005.
41. Юдачева Т.В. Деятельность учителя по организации домашней работы по математике// Нач.шк.,2004, №11.
42. Эльконин Д.Б. Психология игры. - М: Педагогика,2004
Приложение 1
Прохождение лабиринта
Помоги лягушонку, стремящемуся к знаниям, добраться в школу через лабиринт с числовыми выражениями. При этом значения выражений должны составить отрезок натурального ряда.

Такие игры на этапе ознакомления, повторения и закрепления изученного материала выполняют функцию формирования в процессе игры общеучебных умений и навыков, а так же психологических образований, крайне необходимых для активизации учебного процесса.
Приложение 2.
Тест
Задание. Обозначь в игровом поле:
I вариант
Х – числа, которые делятся на 6
О – числа, которые не делятся на 6
II вариант
Х – числа, которые делятся на 7
О – числа, которые не делятся на 7
| На доске |
Рабата учащихся в тетрадях |
Правильный ответ |
| 18 |
81 |
49 |
| 15 |
42 |
9 |
| 63 |
64 |
54 |
|
Вариант I
|
 |
Вариант II
|
 |
Приложение 3
Анкета для учителей.
1. Используете ли вы игры в педагогическом процессе?
2. Какие формы игры вы считаете наиболее успешными в учебном процессе?
3. В каких случаях вы используете игру?
4. На каких этапах урока предпочтительнее на ваш взгляд использовать игру или ее элементы?
5. Какую цель вы чаще всего преследуете, используя дидактическую игру?
6. Считаете ли вы целесообразным использовать игру на уроке?
7. Каких результатов чаще всего вы хотите добиться и удается ли вам это сделать?
8. Любят ли дети игру на уроках?
9. Выполняют ли дети все правила игры?
10. В каких случаях не нужно применять игры?
11. Какие психологические качества ребенка развивает игра?
12. Целесообразно ли использовать игру для развития качеств личности учащегося.
Приложение 4
Анкета для учащихся.
1. Нравится ли тебе, когда учитель использует на уроке игру?
2. Как часто ты бы хотел, чтобы игра использовалась на уроке?
3. Какую форму игры ты любишь больше: индивидуальную, групповую, парную?
4. На каких уроках тебе нравится играть (перечисли)?
5. Бывают ли случаи, когда тебе не нравится игра и почему?
6. Зависит ли твое желание от учителя, использующего игры?
7. Что тебе больше всего нравится в игре?
Приложение 5

Приложение 6

Приложение 7

Приложение 8

|