Контрольная работа
По эконометрики
Обзор корреляционного поля
Эти данные скорее всего можно аппроксимировать при помощи линейной регрессии вида ŷ = а -
b
·
x
,
как самой простой.
Рассчитаем необходимые суммы и запишем их в таблице № 1:
Таблица №1:
| i
|
x
|
y
|
x
²
|
y
²
|
x
·
y
|
ŷ
|
e
|
e²
|
A
(%)
|
| 1
|
2,5 |
69 |
6,25 |
4761 |
172,5 |
66,40 |
2,60 |
6,75 |
3,76 |
| 2 |
3 |
65 |
9 |
4225 |
195 |
64,85 |
0,15 |
0,02 |
0,23 |
| 3 |
3,4 |
63 |
11,56 |
3969 |
214,2 |
63,61 |
-0,61 |
0,37 |
0,97 |
| 4 |
4,1 |
59 |
16,81 |
3481 |
241,9 |
61,44 |
-2,44 |
5,94 |
4,13 |
| 5 |
5 |
57 |
25 |
3249 |
285 |
58,65 |
-1,65 |
2,71 |
2,89 |
| 6 |
6,3 |
55 |
39,69 |
3025 |
346,5 |
54,61 |
0,39 |
0,15 |
0,70 |
| 7 |
7 |
54 |
49 |
2916 |
378 |
52,44 |
1,56 |
2,43 |
2,89 |
| Сумма:
|
31,3 |
422 |
157,31 |
25626 |
1833,1 |
422,00 |
0,00 |
18,38 |
15,57 |
| Среднее:
|
4,471 |
60,286 |
22,473 |
3660,857 |
261,871 |
- |
- |
- |
2,22% |
Ковариация между y
и x
рассчитывается по формуле 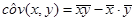 , где , где 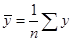 , , 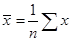 , , 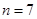 . Дисперсия и среднее квадратическое отклонение для x
и y
находим по формулам:
. Дисперсия и среднее квадратическое отклонение для x
и y
находим по формулам:
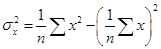 = 2,479, = 2,479, 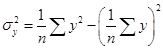 = 26,490, = 26,490, 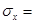 1,575, 1,575,  5,147. 5,147.
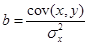 = -7,692 / 2,479 = -3,103; = -7,692 / 2,479 = -3,103; 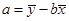 = 60,286 + 3,103 · 4,471 = 74,159 = 60,286 + 3,103 · 4,471 = 74,159
Получили уравнение регрессии: ŷ = 74,159 - 3,103·х
(округлено до сотых).
Оцениваем качество полученной линейной модели:
а) TSS= 25624 - (31,3²) : 7 = 185,492; RSS = TSS - ESS= 185,429 - 18,38 = 176,051, где ESS= 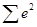 = 18,38 (в таблице №1); F - статистика = RSS · (n - m - 1) : ESS = 176,051 · ·5 :18,38 = 45,45. = 18,38 (в таблице №1); F - статистика = RSS · (n - m - 1) : ESS = 176,051 · ·5 :18,38 = 45,45.
Табличное значение на 1% уровне значимости равно 16,26 (см. таблицу распределения Фишера - Снедекора). Фактическое значение F - статистики больше табличного на 1% уровне значимости, следовательно уравнение регрессии в целом значимо и на 5% уровне значимости.
б) Средняя ошибка аппроксимации равна (ΣА)/7 = ((ΣIy-ŷI: y) · 100%) / 7 = 15,57 / 7 = =2,22%, что говорит о хорошей аппроксимации зависимости моделью (2,22% < 6%).
Вывод: модель получилась приемлемая (в смысле аппроксимации).
в) Коэффициент корреляции находим по формуле: 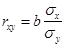 = -0,949: сильная обратная линейная зависимость. = -0,949: сильная обратная линейная зависимость.
г) Коэффициент детерминации находим следующим образом: 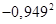 = 0,901 или вариация x
определяет вариацию y
на 90,1%. = 0,901 или вариация x
определяет вариацию y
на 90,1%.
Проверка на соответствие условиям теоремы Гаусса - Маркова
а) По таблице №2 рассчитаем статистику Дарбина - Уотсона:
Таблица №2
| i
|
e²
|
e
|
e
i-1
|
(e
i
-e
i-1
)²
|
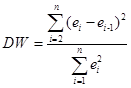 =16,050 : 18,38 = 0,8734. =16,050 : 18,38 = 0,8734.
|
| 1 |
6,75 |
2,60 |
- |
- |
| 2 |
0,02 |
0,15 |
2,598 |
5,996 |
| 3 |
0,37 |
-0,61 |
0,149 |
0,576 |
| 4 |
5,94 |
-2,44 |
-0,610 |
3,342 |
| 5 |
2,71 |
-1,65 |
-2,438 |
0,628 |
| 6 |
0,15 |
0,39 |
-1,646 |
4,134 |
| 7 |
2,43 |
1,56 |
0,388 |
1,373 |
| Итого: |
18,38 |
- |
-1,559 |
16,050 |
Полученное значение попадает в область неопределённости: DW
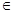 (0,7; 1,35). Это значит, что для прояснения вопроса относительно автокорреляции остатков необходимо дальнейшее исследование ряда остатков другими методами, в которых отсутствует зона неопределённости. (0,7; 1,35). Это значит, что для прояснения вопроса относительно автокорреляции остатков необходимо дальнейшее исследование ряда остатков другими методами, в которых отсутствует зона неопределённости.
б) Воспользуемся тестом
серий Бройша - Годфри:
Таблица №3
| t
|
e
t
|
e
t-1
|
e²
t-1
|
e
t
·e
t-1
|
ê
t
|
(y-bx)
²
|
| 1 |
2,598 |
0,149 |
0,022 |
0,387 |
0,074 |
6,371 |
| 2 |
0,149 |
-0,610 |
0,372 |
-0,091 |
-0,302 |
0,204 |
| 3 |
-0,610 |
-2,438 |
5,944 |
1,487 |
-1,208 |
0,358 |
| 4 |
-2,438 |
-1,646 |
2,709 |
4,013 |
-0,816 |
2,632 |
| 5 |
-1,646 |
0,388 |
0,151 |
-0,639 |
0,192 |
3,379 |
| 6 |
0,388 |
1,559 |
2,430 |
0,605 |
0,773 |
0,148 |
| Итого: |
-1,559
|
-2,598
|
11,628
|
5,763
|
-1,287 |
13,092 |
На основании полученных данных построим уравнение регрессии без свободного члена вида ŷ=b·x.
При этом стандартная ошибка коэффициента регрессии b
, рассчитанная по формуле:
Реклама

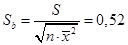 , ,
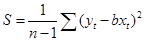 , , 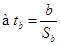 = 1,181, = 1,181,
что меньше значения t
табл.
=
2,57. Это означает, что автокорреляция первого уровня отсутствует.
Однако следует отметить, что и тест Дарбина - Уотсона и тест серий Бройша - Годфри применяются только для выборок достаточно большого размера[1]
, в то время как предложенная нам для анализа выборка состоит только лишь из семи значений.
в) При помощи критерия серий
проверим случайность распределения уровней ряда остатков. С 95% вероятностью распределение ряда остатков считается случайным, если одновременно выполняются два неравенства:
1) 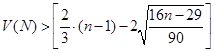
общее число серий должно быть больше
двух, и 2) 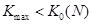 - максимальная длина серии должна быть строго меньше
пяти. - максимальная длина серии должна быть строго меньше
пяти.
Данные для расчётов получаем из таблицы № 4.
Таблица № 4.
Критерий серий линейная модель не проходит:
| ei
|
ei
- ei
-1
|
серии |
Число серий = 2, Продолжительность самой длинной серии
равна 3.
2 = 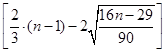 = [2.079] = 2. (не выполняется), = [2.079] = 2. (не выполняется),
хотя 3 < 5. Значит уровни распределены не случайно.
|
| 0,149 |
-2,449 |
+ |
| -0,610 |
-0,759 |
+ |
| -2,438 |
-1,828 |
+ |
| -1,646 |
0,792 |
- |
| 0,388 |
2,033 |
- |
| 1,559 |
1,172 |
- |
г) Соответствие ряда остатков нормальному закону распределения проверяем, используем RS-критерий:
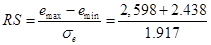 = 2,63, где = 2,63, где 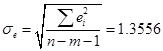 . .
Значение нашего RS-критерия для 7 наблюдений практически попадает в интервал [2,67 3,69], (для 10 наблюдений) хотя и этот критерий определён для выборок более 10 единиц.
д) При помощи теста ранговой корреляции Спирмена определяем отсутствие или наличие гетероскедастичности.
Таблица № 5.
| Ранг Х
|
Х
|
I ei
I |
Ранг еi
|
Di
|
D²i
|
Коэффициент ранговой кореляции определяется по формуле: 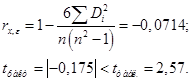
|
| 1 |
2,5 |
2,60 |
7 |
-6 |
36 |
| 2 |
3 |
0,15 |
4 |
-2 |
4 |
| 3 |
3,4 |
0,61 |
3 |
0 |
0 |
| 4 |
4,1 |
2,44 |
1 |
3 |
9 |
| 5 |
5 |
1,65 |
2 |
3 |
9 |
| 6 |
6,3 |
0,39 |
5 |
1 |
1 |
| 7 |
7 |
1,56 |
6 |
1 |
1 |
Так как абсолютное значение статистики коэффициента ранговой корелляции 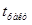 =0,175 оказалась значительно меньше табличного значения =0,175 оказалась значительно меньше табличного значения 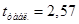 , то гетероскедастичность отсутствует. , то гетероскедастичность отсутствует.
Вывод: линейная модель не соответствует всем предпосылкам регрессионного анализа (условиям теоремы Гаусса-Маркова) и, хотя она пригодна для прогнозирования, но возникает вопрос о её значимости.
Доверительные интервалы для параметра
b
регрессии
Стандартные ошибки для параметров регрессии находим по формулам:
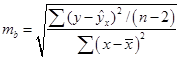 = 0,46, = 0,46,
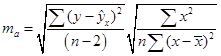 = 2,18. = 2,18.
Проверим на статистическую значимость коэффициент b
модели, для чего рассчитаем t
-статистику по формуле 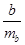 . Полученнаяt
-статистика равна -6,742, что по модулю больше табличного значения t
=
2,57. Экономически этот параметр интерпретируется так: при изменении дохода потребителей на одну единицу объёмы продаж изменятся на -3,103 ед. . Полученнаяt
-статистика равна -6,742, что по модулю больше табличного значения t
=
2,57. Экономически этот параметр интерпретируется так: при изменении дохода потребителей на одну единицу объёмы продаж изменятся на -3,103 ед.
Проверим на статистическую значимость коэффициент a
модели, для чего рассчитаем t
-статистику по формуле 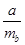 . Полученная t
-статистика равна 33,992, что больше табличного значения t
=
2,57. Доверительный интервал параметраb
определяем по формуле: . Полученная t
-статистика равна 33,992, что больше табличного значения t
=
2,57. Доверительный интервал параметраb
определяем по формуле:
Реклама

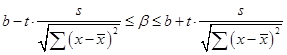 ; ;
s = 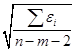 = 1,917, = 1,917,
Доверительный интервал параметраb
составляет 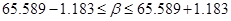 ; или ; или 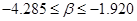 (t
табл.
= 2.57, Δ = 2,57 · 0,4602 = 1,1827). (t
табл.
= 2.57, Δ = 2,57 · 0,4602 = 1,1827).
Проведённый анализ коэффициентов регрессии говорит о том, что параметры регрессии значимы, кроме того и уравнение регрессии в целом значимо на 1% уровне значимости (cм. выше). Это позволяет использовать построенную нами модель для получения прогнозов.
Точечный и интервальный прогнозы
Вначале находим точечный прогноз для значения х
, на 25% превышающего среднее значение 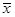 = 4,47 ( т.е. при = 4,47 ( т.е. при 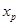 = 5,589), = 5,589), 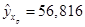 . Тогда стандартная ошибка прогноза составит: . Тогда стандартная ошибка прогноза составит:
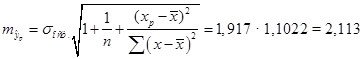 , ,
t
табл.
= 2.57, Δ = 2,57 · 2,18 = 5,604.
Интервальный прогноз для точечного прогноза при 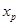 = 5,589 ( = 5,589 (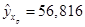 ) составит: ) составит:  или или 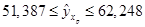 . .
[1]
Кристофер Доугерти. Введение в эконометрику. М.: Инфра М, 2001. С. 238.
|