|
Среднегодовая численность населения области выглядит следующим образом:
| Год |
Среднегодовая численность населения, тыс.чел. |
| 1992 |
2528,0 |
| 1993 |
2655,0 |
| 1994 |
2689,0 |
| 1995 |
2722,0 |
| 1996 |
2747,4 |
| 1997 |
2747,7 |
| 1998 |
2750,5 |
| 1999 |
2747,9 |
| 2000 |
2739,0 |
Рассчитать абсолютные (цепные и базисные) и средние показатели динамики.
Решение
1. Требуемые показатели рассчитываются по формулам:
· Абсолютный прирост:

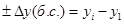
· Темп роста
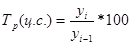
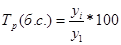
· Темп прироста:
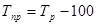
Полученные данные представим в таблице:
| Год |
Среднегодовая численность населения, тыс. чел. |
Абсолютный прирост, млн. руб. |
Темпы роста, % |
Темпы прироста, % |
| к баз. |
к отч. |
к баз. |
к отч. |
к баз. |
к отч. |
| 1992 |
2528,0 |
0 |
- |
100 |
- |
0 |
- |
| 1993 |
2655,0 |
127 |
127 |
105,0 |
105,0 |
5 |
5 |
| 1994 |
2689,0 |
161 |
34 |
106,4 |
101,3 |
6,4 |
1,3 |
| 1995 |
2722,0 |
194 |
33 |
107,7 |
101,2 |
7,7 |
1,2 |
| 1996 |
2747,4 |
219,4 |
25,4 |
108,7 |
100,9 |
8,7 |
0,9 |
| 1997 |
2747,7 |
219,7 |
0,3 |
108,7 |
100 |
8,7 |
0 |
| 1998 |
2750,5 |
222,5 |
2,8 |
108,8 |
100,1 |
8,8 |
0,1 |
| 1999 |
2747,9 |
219,9 |
-2,6 |
108,7 |
99,9 |
8,7 |
-0,1 |
| 2000 |
2739,0 |
211 |
-8,9 |
108,3 |
99,7 |
8,3 |
-0,3 |
Среднегодовой абсолютный прирост определим по формуле:
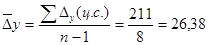 тыс. чел. тыс. чел.
Среднегодовые темпы роста и прироста:
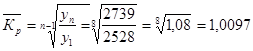  или 100,97% или 100,97%
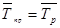
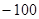 =
100,97-100 = 0,97%,
=
100,97-100 = 0,97%,
то есть ежегодно уровни ряда возрастали в среднем на 0,97%.
По одному из предприятий региона имеются следующие данные об объеме производства макаронных изделий:
| Год |
Объем производства, т. |
| 1990 |
138,4 |
| 1991 |
155,4 |
| 1992 |
165,4 |
| 1993 |
168,1 |
| 1994 |
173,9 |
| 1995 |
178,1 |
| 1996 |
184,2 |
| 1997 |
189,7 |
| 1998 |
190,5 |
| 1999 |
200,2 |
| 2000 |
209,7 |
Определить:
1. среднегодовое производство макаронных изделий;
2. базисные, цепные и среднегодовые показатели абсолютного прироста, темпов роста и темпов прироста производства макаронных изделий;
3. проверьте ряд динамики производства макаронных изделий на наличие тренда. Используя метод аналитического выравнивания, постройте уравнение прямой;
4. изобразите динамику производства макаронных изделий на графике.
Решение
1. Данный динамический ряд является интервальным, поэтому для определения среднегодового производства используем формулу арифметической простой:
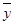 = =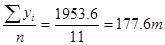 , ,
то есть в среднем в год производится 177,6 тонн макаронных изделий.
2. Базисные, цепные и среднегодовые показатели абсолютного прироста, темпов роста и темпов прироста производства макаронных изделий рассчитываются по формулам:
· Абсолютный прирост:

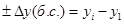
· Темп роста:
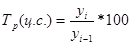
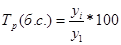
· Темп прироста:
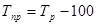
Полученные данные представим в таблице:
| Год |
Объем производства, т. |
Абсолютный прирост, млн. руб. |
Темпы роста, % |
Темпы прироста, % |
| к баз. |
к отч. |
к баз. |
к отч. |
к баз. |
к отч. |
| 1990 |
138,4 |
0 |
- |
100 |
- |
0 |
- |
| 1991 |
155,4 |
17 |
17 |
112,28 |
112,28 |
12,28 |
12,28 |
| 1992 |
165,4 |
27 |
10 |
119,51 |
106,44 |
19,51 |
6,44 |
| 1993 |
168,1 |
29,7 |
2,7 |
121,46 |
101,63 |
21,46 |
1,63 |
| 1994 |
173,9 |
35,5 |
5,8 |
125,65 |
103,45 |
25,65 |
3,45 |
| 1995 |
178,1 |
39,7 |
4,2 |
128,68 |
102,42 |
28,68 |
2,42 |
| 1996 |
184,2 |
45,8 |
6,1 |
133,09 |
103,43 |
33,09 |
3,43 |
| 1997 |
189,7 |
51,3 |
5,5 |
137,07 |
102,99 |
37,07 |
2,99 |
| 1998 |
190,5 |
52,1 |
0,8 |
137,64 |
100,42 |
37,64 |
0,42 |
| 1999 |
200,2 |
61,8 |
9,7 |
144,65 |
105,09 |
44,65 |
5,09 |
| 2000 |
209,7 |
71,3 |
9,5 |
151,52 |
104,75 |
51,52 |
4,75 |
3. Рассчитаем уравнение тренда ряда динамики.
| Годы |
Объем производства, т. |
t |
t2
|
yt |
 |
| 1990 |
138,4 |
1 |
1 |
138,4 |
-151,88 |
| 1991 |
155,4 |
2 |
4 |
310,8 |
-101,63 |
| 1992 |
165,4 |
3 |
9 |
196,2 |
-51,38 |
| 1993 |
168,1 |
4 |
16 |
672,4 |
-1,13 |
| 1994 |
173,9 |
5 |
25 |
869,5 |
49,12 |
| 1995 |
178,1 |
6 |
36 |
1068,6 |
99,37 |
| 1996 |
184,2 |
7 |
49 |
1289,4 |
149,62 |
| 1997 |
189,7 |
8 |
64 |
1517,6 |
199,87 |
| 1998 |
190,5 |
9 |
81 |
1714,5 |
250,12 |
| 1999 |
200,2 |
10 |
100 |
2002 |
300,37 |
| 2000 |
209,7 |
11 |
121 |
2306,7 |
350,62 |
| Итого |
1953,6 |
66 |
506 |
12086,1 |
1093,07 |
Для выравнивания ряда динамики по прямой следует получить уравнение:  =a0
+a1
t. =a0
+a1
t.
Для расчета параметров а0
и а1
решается система нормальных уравнений:
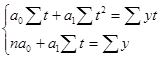
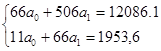
Решив систему, получаем: a0
=-202,13, a1
=50,25.
Уравнение тренда примет вид:  =-202,13+50,25t. =-202,13+50,25t.
Ряд выровненных значений  характеризует тенденцию стабильного увеличения выпуска продукции. характеризует тенденцию стабильного увеличения выпуска продукции.
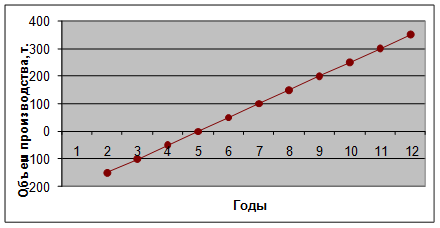
4. Изобразим динамику производства макаронных изделий на графике.

Имеются данные о вводе жилых домов по одной из строительных компаний:
| Год |
Введено общей площади, тыс. кв. м. |
| 1990 |
33 |
| 1991 |
35 |
| 1992 |
35 |
| 1993 |
37 |
| 1994 |
42 |
| 1995 |
46 |
| 1996 |
48 |
| 1997 |
50 |
| 1998 |
52 |
| 1999 |
54 |
| 2000 |
58 |
Определить:
1. среднегодовой ввод жилых домов;
2. базисные, цепные и среднегодовых показатели абсолютного прироста, темпов роста и прироста ввода жилых домов.
3. на основе средних абсолютных приростов и темпов роста определить ожидаемый уровень ввода жилых домов в 2005 г.
Реклама

4. изобразить динамику ввода жилых домов на графике.
Решение
1. Данный динамический ряд является интервальным, поэтому для определения среднегодового производства используем формулу арифметической простой:
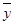 = =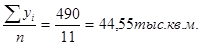 , ,
то есть в среднем в год вводится 44,55 тыс. кв. м
2. Требуемые показатели рассчитываются по формулам:
· Абсолютный прирост:

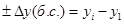
· Темп роста:
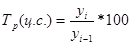
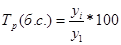
· Темп прироста:
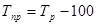
Полученные данные представим в таблице:
| Год |
Введено общей площади, тыс. кв. м. |
Абсолютный прирост, млн. руб. |
Темпы роста, % |
Темпы прироста, % |
| к баз. |
к отч. |
к баз. |
к отч. |
к баз. |
к отч. |
| 1990 |
33 |
0 |
- |
100 |
- |
0 |
- |
| 1991 |
35 |
2 |
2 |
106,06 |
106,06 |
6,06 |
6,06 |
| 1992 |
35 |
2 |
0 |
106,06 |
100 |
6,06 |
0 |
| 1993 |
37 |
4 |
2 |
112,12 |
105,71 |
12,12 |
5,71 |
| 1994 |
42 |
9 |
5 |
127,27 |
113,51 |
27,27 |
13,51 |
| 1995 |
46 |
13 |
4 |
139,39 |
109,52 |
39,39 |
9,52 |
| 1996 |
48 |
15 |
2 |
145,45 |
104,35 |
45,45 |
4,35 |
| 1997 |
50 |
17 |
2 |
151,51 |
104,17 |
51,51 |
4,17 |
| 1998 |
52 |
19 |
2 |
157,58 |
104 |
57,58 |
4 |
| 1999 |
54 |
21 |
2 |
163,64 |
103,85 |
63,64 |
3,85 |
| 2000 |
58 |
25 |
4 |
175,76 |
107,41 |
75,76 |
7,41 |
Среднегодовой абсолютный прирост определим по формуле:
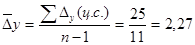 тыс. кв. м. тыс. кв. м.
Среднегодовые темпы роста и прироста:
  или 105,8% или 105,8%
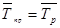
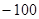 =
105,8-100 = 5,8%,
=
105,8-100 = 5,8%,
то есть ежегодно уровни ряда возрастали в среднем на 5,8%.
3. Если принять во внимание ввод жилых домов в 2000 и рассчитанный выше абсолютный прирост, то в 2005 году ввод жилых домов составит приблизительно 69,35 тыс. кв. м. (58+2,27*5).
4. Изобразим динамику ввода жилых домов на графике:

Задача 4
Имеются данные о ценах и количестве проданных товаров:
| Вид товара |
Единица измерения |
Цена за единицу, руб. |
Реализовано, тыс. ед. |
| Базисный период |
Отчетный период |
Базисный период |
Отчетный период |
| Мясо |
кг |
80 |
110 |
600 |
500 |
| Молоко |
л |
15 |
25 |
800 |
900 |
Определить:
1. общий индекс цен;
2. общий индекс физического объема товарооборота;
3. общий индекс товарооборота.
Решение
1. Общий индекс цен определим по формуле:
Ip
=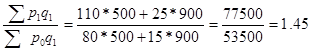 или 145%. или 145%.
Следовательно, цены увеличились в среднем на 45%.
2. Общий индекс физического объема оборота рассчитаем по формуле:
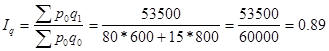 или 89%. или 89%.
Следовательно, физическая масса продажи снизилась на 11%.
3. Общий индекс оборота в действующих ценах:
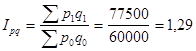 или129%. или129%.
Взаимосвязь: 1,45*0,89=1,29
В коммерческом банке в порядке собственно-случайной выборки обследовано 5% кредитных договоров, в результате чего установлено:
| Группы договоров с ссудозаемщиками по размеру кредита, тыс. руб. |
Число договоров с ссудозаемщиками |
| До 200 |
47 |
| 200-600 |
117 |
| 600-1400 |
105 |
| 1400-3000 |
47 |
| 3000 и более |
34 |
| ИТОГО |
350 |
Определить:
1. по договорам, включенным в выборку:
а) средний размер выданного ссудозаемщиком кредит
а;
б) долю ссудозаемщиков, получивших кредит в размере более 3000 тыс. руб.
2. с вероятностью 0,954 пределы, в которых можно ожидать средний размер выданного ссудозаемщикам кредита и доли судозаемщиков, получивших кредит в размере более 3000 тыс. руб. в целом по отделению банка.
Решение
1. Закроем интервалы, определим центры интервалов, рассчитаем размер кредитов во всех договорах и занесем расчетные показатели в таблицу:
| Группы договоров с ссудозаемщиками по размеру кредита, тыс. руб. |
Число договоров с ссудозаемщиками (fi
) |
Группы договоров с ссудозаемщиками по размеру кредита, тыс. руб. |
Середина интервала
(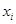 ) )
|
Размер кредитов во всех договорах, тыс. руб. (xi
fi
) |
x2
f |
| До 200 |
47 |
0-200 |
100 |
4700 |
470000 |
| 200-600 |
117 |
200-600 |
400 |
46800 |
18720000 |
| 600-1400 |
105 |
600-1400 |
1000 |
105000 |
105000000 |
| 1400-3000 |
47 |
1400-3000 |
2200 |
103400 |
227480000 |
| 3000 и более |
34 |
3000-4600 |
3800 |
129200 |
490960000 |
| ИТОГО |
350 |
- |
- |
389100 |
842630000 |
а) для определения среднего размера выданного ссудозаемщиком кредита воспользуемся формулой средней арифметической взвешенной:
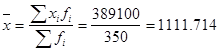 тыс. руб. тыс. руб.
б)доля ссудозаемщиков, получивших кредит в размере более 3000 тыс. руб. равна:
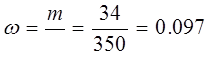 или 9,7%. или 9,7%.
2. Определим с вероятностью 0,954 пределы, в которых можно ожидать средний размер выданного ссудозаемщикам кредита и доли судозаемщиков, получивших кредит в размере более 3000 тыс. руб. в целом по отделению банка.
Дисперсия рассчитывается по формуле:
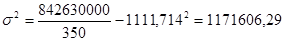
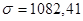
Средняя ошибка выборки составит:
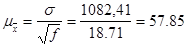
t=2
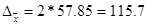 тыс. руб. тыс. руб.
Реклама

Установим границы: 1111,714-115,7≤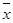 ≤1111,714+115,7 ≤1111,714+115,7
996,014≤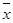 ≤1227,414 ≤1227,414
Значит, на основании проведенного обследования с вероятностью 0,954 можно заключить, что средний размер выданного ссудозаемщикам кредита, получивших кредит в размере более 3000 тыс. руб., в целом по отделению банка лежит в пределах от 996,014 до 1227,414 тыс. руб.
1. Теория статистики: Учебник / Р. А. Шмойлова, В. Г. Минашкин, Н. А. Садовникова, Е. Б. Шувалова; Под ред. Р. А. Шмойловой. – 4-е изд., перераб. и доп. – М.: Финансы и статистика, 2005. – 656с.
2. Гусаров В.М. Статистика: Учебное пособие для вузов. - М.: ЮНИТИ-ДАНА, 2001.
3. Октябрьский П. Я. Статистика: Учебник. – М.: ТК Велби, Изд-во Проспект, 2005. – 328 с.
4. Сборник задач по теории статистики: Учебное пособие/ Под ред.проф. В.В.Глинского и к.э.н., доц. Л.К.Серга. Изд.З-е.- М.:ИНФРА-М; Новосибирск: Сибирское соглашение, 2002.
5. Статистика: Учебное пособие/Харченко Л-П., Долженкова В.Г., Ионин В.Г. и др., Под ред. В.Г.Ионина. - Изд. 2-е, перераб. и доп. - М.: ИНФРА-М.2003.
|