1.
Анализ распределения элементов статистического ряда
Исходная таблица содержит данные по количеству выявленных лиц, совершивших кражи чужого имущества в населенных пунктах А и Б с 1961 по 2000 гг. В то время было принято измерять временные интервалы пятилетиями. В интервале с 1961 г. по 2000 г. укладывается ровно 8 пятилеток.
Таблица 1. Группировочная таблица по числу выявленных лиц в населенных пунктах А и Б с 1 по 8 пятилетку
| Пятилетка |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Населенный пункт А |
173 |
109 |
236 |
137 |
159 |
235 |
79 |
116 |
| Населенный пункт Б |
360 |
380 |
339 |
387 |
454 |
286 |
181 |
256 |
С точки зрения статистики у нас появились два вариационных ряда для признаков Х (населенный пункт А) и У (населенный пункт Б) с одинаковым числом вариантов n = 8 без выделения частот и относительных частот. Одновременно эти ряды являются рядами динамики для одного и того же временного интервала с 1 по 8 пятилетку. Графически они могут быть представлены в виде полигонов как ряды динамики.
В рамках данной темы целесообразнее рассматривать интервальные ряды для распределения числа выявленных лиц по населенным пунктам А и Б.
Таблица 2. Интервальные ряды для числа выявленных лиц по населенным пунктам А и Б
| № |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| А |
173 |
109 |
236 |
137 |
159 |
235 |
79 |
116 |
| Б |
360 |
380 |
339 |
387 |
454 |
286 |
181 |
256 |
Таблица 2 служит таблицей частот. Для построения гистограмм лучше рассмотреть относительные частоты.
Таблица 3. Статистическое распределение интервальных рядов
| i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| (Wi) А |
0,14 |
0,09 |
0,19 |
0,11 |
0,13 |
0,19 |
0,06 |
0,09 |
| (Wi) Б |
0,14 |
0,14 |
0,13 |
0,15 |
0,17 |
0,11 |
0,07 |
0,10 |
Относительные частоты вычисляются по формуле:
Wi = ni
/n, (n = 1, 2, 3, …, 8),
где nа
= 1244, nб
= 2643
Диаграмма 1. Гистограмма относительных частот числа выявленных лиц по населенному пункту А
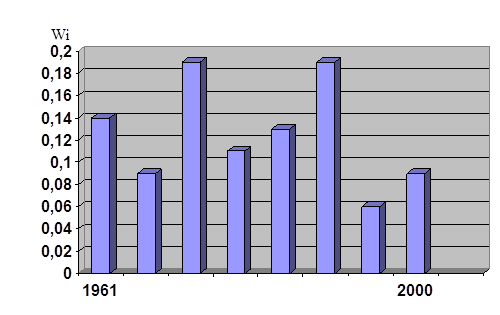
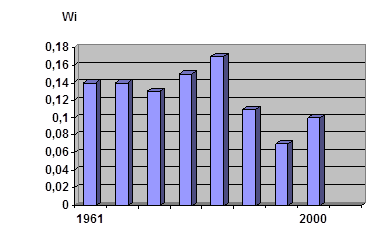
Диаграмма 2. Гистограмма относительных частот числа выявленных лиц по населенному пункту Б
Населенный пункт А характеризуется неравномерностью распределения числа выявленных лиц, совершивших кражи. Пики преступности данного вида приходятся на 3 и 6 пятилетки. Относительное снижение преступности отмечается в 7 пятилетке (выявлено всего 79 лиц, относительная частота на гистограмме составил W7
= 0,06). В целом усматривается незначительное снижение уровня преступности.
В населенном пункте Б уровень рассматриваемой преступности выше, чем в населенном пункте А. Обострение преступности произошло в 5 пятилетки. 7-ая пятилетка была спокойнее остальных.
2. Вычисление основных статистических параметров
Таблица 4. Основные статистические параметры рядов распределения
| Среднее значение |
Среднее квадратичное отклонение |
Асимметрия |
Эксцесс |
| А |
155,5 |
53,661 |
0,33 |
46,135 |
| Б |
330,375 |
80,404 |
-0,39 |
-0,66 |
Среднее значение вычисляется по формуле:
Х = 1/8 ∑х
Среднее квадратичное отклонение
б = √х2
– (х)2
Асимметрия
As = М3
/ б3
Эксцесс
Ех = М4
/ б4
где М3
= 1/8 ∑(хi
– х)3
,
М4
= 1/8 ∑(хi
– х)4
.
Отметим промежуточные результаты:
М3
(А) = 51664,875;
М4
(А) = 407404409,3;
М3
(Б) = -201499,2539;
М4
(Б) = 97879670,62.
Реклама

Видно, что в населенном пункте Б средний уровень преступности почти в 2 раза больше, чем в населенном пункте А.
У соответствующих двух рядов распределения разный характер асимметрии. Довольно большой эксцесс у первого признака, у второго – незначительный.
Заметим, что нулевое значение эксцесса характерно для нормального закона распределения (распределения Гаусса).
3.
Анализ динамических рядов
Таблица 5. Ряды динамики числа выявленных лиц по населенным пунктам А и Б
| Номер пятилетки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Х |
173 |
109 |
236 |
137 |
159 |
235 |
79 |
116 |
| У |
360 |
380 |
339 |
387 |
454 |
286 |
181 |
256 |
Таблица 6. Основные показатели динамики по населенному пункту А
| Пятилетка |
Число лиц |
Абсолютный прирост (∆) |
Темп роста Тр, % |
Темп прироста Тпр, % |
Абсолютное значение 1% прироста |
цеп
ной
|
базис
ный
|
цеп
ной
|
базисный |
цепной |
базисный |
| 1 |
173 |
- |
- |
100,0 |
100,0 |
0,0 |
0,0 |
- |
| 2 |
109 |
-64 |
-64 |
63,0 |
-37,0 |
-37,0 |
-37,0 |
1,73 |
| 3 |
236 |
127 |
63 |
216,5 |
136,4 |
116,5 |
36,4 |
1,09 |
| 4 |
137 |
-99 |
-36 |
58,1 |
79,2 |
-41,9 |
-20,8 |
2,36 |
| 5 |
159 |
22 |
-14 |
116,1 |
91,9 |
16,1 |
-8,1 |
1,37 |
| 6 |
235 |
76 |
63 |
147,8 |
135,8 |
47,8 |
35,8 |
1,59 |
| 7 |
79 |
-166 |
-94 |
33,6 |
45,7 |
-66,4 |
-54,3 |
2,35 |
| 8 |
116 |
37 |
-57 |
146,8 |
67,1 |
46,8 |
-32,9 |
0,79 |
| В среднем |
155,5 |
-8 |
82,5 |
-17,5 |
Таблица 7. Основные показатели динамики по населенному пункту Б
| Пятилетка |
Число лиц |
Абсолютный прирост (∆) |
Темп роста Тр, % |
Темп прироста Тпр, % |
Абсолютное значение 1% прироста |
цеп
ной
|
базис
ный
|
цеп
ной
|
базисный |
цепной |
базисный |
| 1 |
360 |
- |
- |
100,0 |
100,0 |
0,0 |
0,0 |
- |
| 2 |
380 |
20 |
20 |
105,6 |
105,6 |
5,6 |
5,6 |
3,6 |
| 3 |
339 |
-41 |
-21 |
89,2 |
94,2 |
-10,8 |
-5,8 |
3,8 |
| 4 |
387 |
48 |
27 |
114,2 |
107,5 |
14,2 |
7,5 |
3,39 |
| 5 |
454 |
67 |
94 |
117,3 |
126,1 |
17,3 |
26,1 |
3,87 |
| 6 |
286 |
-132 |
-74 |
63,0 |
79,4 |
-37,0 |
-20,6 |
4,54 |
| 7 |
181 |
-105 |
-179 |
63,3 |
50,3 |
-36,7 |
-49,7 |
2,86 |
| 8 |
256 |
75 |
-104 |
141,1 |
71,1 |
41,4 |
-28,9 |
1,81 |
| В среднем |
330,4 |
-15 |
87,2 |
-12,8 |
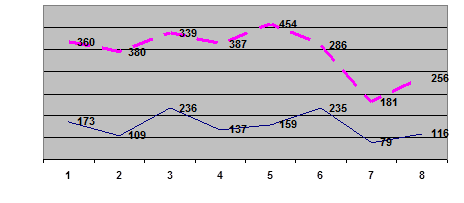
Диаграмма 3. Графическое изображение рядов динамики по населенным пунктам А (сплошная линия) и Б (пунктирная линия)
При заполнении таблиц 6 и 7 использованы формулы для цепной формы расчета:
∆ = у – уi
,
Тр = уi
/уi – 1
,
Тпр = Тр – 1,
А = уi – 1
/100
и для базисной формы:
∆ = уi
– у0
,
Тр = уi
/у0
,
Тпр = Тр – 1,
∆-
= ∆/7,
Тр-
= 7
√(Тр)1
(Тр)2
… (Тр)7
.
Графики и расчетные таблицы говорят о небольшом снижении уровня краж по населенным пунктам А и Б. В среднем абсолютное снижение больше у населенного пункта Б, а темп снижения больше у пункта А. Но сам уровень преступности все время остается выше в населенном пункте Б.
4. Корреляционная зависимость
Парный коэффициент корреляции
Чху
= ху-
– х-
*у-
/бх
бу
.
После вычисления среднего значения
ху-
= 1/8∑хi
yi
= 52514,25
получаем Чху
= 0,26
Корреляционная зависимость слабая.
У величины Чху
как у случайной величины есть среднее квадратичное отклонение
mч
= √1-ч2
/n-2 = 0,4
Величина tч
= ч/ mч
распределена по закону Стьюдента со степенью свободы к = n – 2 = 6.
При уровне значимости а = 0,05
Табличное значение
tтабл
= 2,4469
Предельная ошибка
∆ч = tтабл
* mч
= 0,98.
Поскольку вообще -1≤чху
≤1, то вычисленная ошибка ∆ч = 0,98 смысла не имеет. Причина кроется в слабой тесной связи признаков х и у.
5. Уравнение регрессии
Линейная регрессия у = а + вх рассчитывается по формуле:
ỷ – у-
= ч бу
/бх
(х-х-
),
ỷ – 330,4 = 0,26 * 80,404/53,661 (х – 155,5),
ỷ = 0,39х + 269,8
Критерий Фишера имеет расчетное значение
F = (tч)4
= (ч/ mч
)4
= 0.18
При надежности 95% табличное значение Fтабл
= 5,99. со степенями свободы к1
= 1, к2
= 6.
Так как F = 0,18 ‹ 1, следует перейти к обратной величине Fфакт
= 5,55. Но тогда и Fтабл
= 233,97 для степеней свободы к1
= 6, к2
= 1.
Реклама

Мы видим, что все уравнение регрессии не значимо.
Абсолютная ошибка ∆у зависит от конкретного значения х и рассчитывается по формуле:
∆у = бост
√1+1/8 + ∑(х – х-
)2
/8бх
2
,
Где в свою очередь,
бост
= √∑(уi
–ỷi
)2
/6.
По формуле ỷ = 269,8 + 0,39х найдем восемь значений ỷ(х):
337 312 362 323 332 361 301 315
Значит, бост
= 89,373.
Самая малая ошибка ∆у будет при х = х-
:
(∆у)min
= 34,8 * 2,4469 = 232.
Для ошибки это слишком много. Это объясняется слабой теснотой корреляционной зависимости.
6. Обобщение статистических данных и статистический анализ
После группировки исходных данных по пятилетним периодам получились вариационные интервальные ряды.
Поэтому в их ранжировке нет необходимости.
После построения гистограмм выяснилось, что распределения сильно отличаются от распределения Гаусса. Поэтому их исследование с помощью понятий асимметрии и эксцесса становится формальным.
Вычисление средних значений позволило сделать вывод о почти двукратном превышении показателя преступности в населенном пункте Б. Это подтверждает и сравнительная диаграмма 3.
В течение первых шести пятилеток в населенных пунктах А и Б отмечались противоположные тенденции по динамике уровня выявленных лиц, а в последние две пятилетки эти тенденции совпадали. В целом заметно небольшое снижение уровня преступности данного вида. На это указали и расчеты при заполнении таблиц 6 и 7.
Как и ожидалось, корреляционная зависимость показателей по двум населенным пунктам оказалась слабой. Оказалось незначимой и сама регрессионная линейная модель.
По этой причине потеряли практический смысл оценки ошибок для линейного коэффициента корреляции и для прогнозных значений регрессии.
1. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для ВУЗов. М.: ЮНИТИ-ДАНА, 2005.
2. Практикум по эконометрике: Учебное пособие. Под ред. И.И. Елисеевой. М.: Финансы и статистика, 2003.
3. Эконометрика: Учебник. Под ред. И.И. Елисеевой. М.: Финансы и статистика, 2004.
4. Шимко П.Д., Власов М.П. Статистика/ Серия «Учебники, учебные пособия». – Ростов на Дону: Феникс, 2003.
5. Глинский В.В., Ионин В.Г. Статистический анализ: Учебное пособие. М.: ИНФРА-М; Новосибирск: Сибирское соглашение, 2002.
6. Сборник задач по теории статистики: Учебное пособие / Под ред. В.В. Глинского и Л.К. Серга. – М.: ИНФРА-М; Новосибирск: Сибирское соглашение, 2002
|