Задача 1.7
Имеются данные по группе работников промышленного предприятия
| № п/п
|
Выполнение норм выработки, % |
Заработная плата грн. |
№ п/п |
Выполнение норм выработки, % |
Заработная плата грн. |
| 1 |
103,1 |
363 |
16 |
107 |
388 |
| 2 |
105,2 |
382 |
17 |
105,8 |
389 |
| 3 |
106 |
390 |
18 |
97 |
340 |
| 4 |
96,7 |
342 |
19 |
103 |
364 |
| 5 |
114 |
416 |
20 |
108 |
395 |
| 6 |
107 |
404 |
21 |
110 |
410 |
| 7 |
98,5 |
344 |
22 |
100,8 |
362 |
| 8 |
90 |
300 |
23 |
105,3 |
385 |
| 9 |
102,3 |
373 |
24 |
103 |
376 |
| 10 |
106,4 |
378 |
25 |
93,6 |
303 |
| 11 |
104,3 |
367 |
26 |
100,7 |
363 |
| 12 |
103,7 |
364 |
27 |
98 |
345 |
| 13 |
106,9 |
387 |
28 |
101 |
356 |
| 14 |
94 |
310 |
29 |
101,2 |
360 |
| 15 |
108,3 |
406 |
30 |
100 |
350 |
Для изучения зависимости между выполнением норм выработки и заработной платы произведите группировку рабочих по выполнению норм выработки, выделив пять групп с равными интервалами. По каждой группе и в целом совокупности работников подсчитайте:
1) число рабочих;
2) средний процент выполнения норм;
3) среднюю заработную плату;
Результаты представьте в виде таблицы сделайте выводы.
Решение
Величина интервала
h = (xmax
– xmin
) / m = (114 – 90) / 5 = 4,8
Границы интервалов:
90 + 4,8 = 94,8
94,8 + 4,8 = 99,6
99,6 + 4,8 = 104,4
104,4 +4,8 = 109,2
109,2 + 4,8 =114
Следовательно, первая группа рабочих имеет норм выработки 90–94.8%, вторая – 94.8–99.6%, третья – 99,6–104,4%, четвертая – 104,4–109,2%, пятая – 109,2–114% выработки. По каждой группе подсчитаем нормы заработной платы и оформим результаты в виде рабочей таблицы 2.
Таблица 2
№ п/п
|
Выполнение норм выработки, % |
Заработная плата грн. |
| 8 |
90 |
300 |
| 25 |
93,6 |
303 |
| 14 |
94 |
310 |
| Итого |
277,6 |
913 |
| 4 |
96,7 |
342 |
| 18 |
97 |
340 |
| 27 |
98 |
345 |
| 7 |
98,5 |
344 |
| Итого |
390,2 |
1371 |
| 30 |
100 |
350 |
| 26 |
100,7 |
363 |
| 22 |
100,8 |
362 |
| 28 |
101 |
356 |
| 29 |
101,2 |
360 |
| 9 |
102,3 |
373 |
| 24 |
103 |
376 |
| 19 |
103 |
364 |
| 1 |
103,1 |
363 |
| 12 |
103,7 |
364 |
| 11 |
104,3 |
367 |
| Итого |
1123,1 |
3998 |
| 2 |
105,2 |
382 |
| 23 |
105,3 |
385 |
| 17 |
105,8 |
389 |
| 3 |
106 |
390 |
| 10 |
106,4 |
378 |
| 13 |
106,9 |
387 |
| 6 |
107 |
404 |
| 16 |
107 |
388 |
| 20 |
108 |
395 |
| 15 |
108,3 |
406 |
| Итого |
1065,9 |
3904 |
| 21 |
110 |
410 |
| 5 |
114 |
416 |
| Итого |
224 |
826 |
Построим аналитическую таблицу по группировочному признаку (см. таблицу 3).
Таблица 3
| № группы |
Группа рабочих по выработке, % |
Число рабочих, чел. |
Средняя норма выработки, % |
Месячная зарплата, грн. |
| I |
90–94.8 |
3 |
92,53 |
304,3333333 |
| II |
94.8–99.6 |
4 |
97,55 |
342,75 |
| III |
99,6–104,4 |
11 |
102,1 |
363,4545455 |
| IV |
104,4–109,2 |
10 |
106,59 |
390,4 |
| V |
109,2–114 |
2 |
112 |
413 |
| Всего: |
30 |
102,69 |
367,07 |
Построим гистограмму распределения (см. рисунок 1).
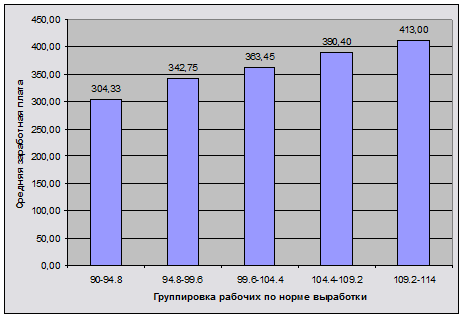
Рисунок 1 – Гистограмма распределения
Вывод:
результаты группировки представлены в таблице 3, они свидетельствуют о том, что с увеличением выработки средняя месячная заработная плата увеличивается, то есть между нормой выработки рабочего и месячной заработной платой существует прямая зависимость. Данные по каждое группе представлены в таблице 3.
Задача 2.08
Имеются данные по трем заводам, вырабатывающим одноименную продукцию «КС‑1»(таблица 4).
Таблица 4
| Завод |
2002 год |
2003 год |
| Затраты времени на единицу продукции, ч. |
Изготовлено продукции, тыс. шт. |
Затраты времени на единицу продукции, ч. |
Затраты времени на всю продукцию, ч. |
| 1 |
2,0 |
2,0 |
1,8 |
3960 |
| 2 |
2,5 |
5,0 |
2,3 |
11500 |
| 3 |
2,2 |
3,0 |
2,0 |
6400 |
Исчислите средние данные времени на всю продукцию по трем заводам в 2002 и 2003 гг. Укажите какие виды средних необходимо применить. Сделайте выводы.
Решение
Согласно условия, имеем:
X
i
- i‑й вариант значения усредняемого признака – времени на изготовление продукции по двум годам (дано для 2002 и 2003 гг.
),
fi
- частота i‑го варианта – изготовлено продукции шт. (дано для 2002 г.
),
Mi
- произведения значения признака и частоты – общие затраты времени на всю продукцию (дано для 2003 г.
).
1) Рассчитаем среднюю затраты времени в 2002 г., используя формулу средней арифметической взвешенной
(так как располагаем данными о значениях и частотах):
Реклама

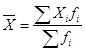 , ,
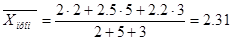 ч ч
2) Рассчитаем среднюю затраты времени в 2003 году, используя формулу средней гармонической взвешенной
(так как располагаем данными о значениях, не располагаем данными о частотах, но имеем произведения значений и частот):
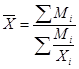 , ,
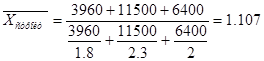 ч ч
3) Вывод:
средние затраты времени в 2002 г. составили 2,31 ч. (рассчитано по формуле средней арифметической взвешенной, так как располагаем данными о значениях и частотах), в 2003 г. – 1,107 ч. (рассчитано по формулесредней гармонической взвешенной, так как располагаем данными о значениях и произведения значений и частот). Средняя время на изготовление продукции в 2002 г. больше на 1,203 ч., чем в 2003 г.
Задача 3.11
Распределение 260 металлорежущих станков на заводе характеризуется данными, представленными в таблице 5. Вычислите:
1) Средний срок службы станка;
2) Моду и медиану;
3) Среднее линейное отклонение;
4) Дисперсию и среднее квадратичное отклонение;
5) Коэффициент вариации;
Решение
Таблица 5
| Срок службы, лет
|
до 4 |
4–8 |
8–12 |
12–16 |
свыше 16 |
Итого |
| Количество станков
|
50 |
90 |
40 |
50 |
30 |
260 |
Способ моментов основан на применении математических свойств средней арифметической взвешенной и позволяет значительно упростить технику вычисления. Расчет производится по формуле
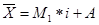 , ,
где 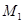 - момент первого порядка, - момент первого порядка,
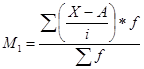
i
– величина интервала (шаг),
A
–
постоянная величина, на которую уменьшаются все значения признака. В вариационных рядах с равными интервалами в качестве такой величины принимается вариант ряда, с наибольшей частотой.
Построим рабочую таблицу (см. таблицу 6).
Имеем
i=4, A=6
(приf max=9
0)
Таблица 6
| Срок службы лет |
количество станков |
Середина интервала, X
|
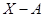
|
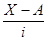
|
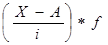
|
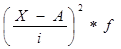
|
| до 4 |
50 |
2 |
-4 |
-1 |
-50 |
50 |
| 4–8 |
90 |
6 |
0 |
0 |
0 |
0 |
| 8–12 |
40 |
10 |
4 |
1 |
40 |
40 |
| 12–16 |
50 |
14 |
8 |
2 |
100 |
200 |
| свыше 16 |
30 |
18 |
12 |
3 |
90 |
270 |
| Итого: |
260 |
20 |
180 |
560 |
Определим момент первого порядка
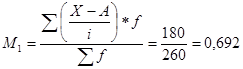
Определим момент второго порядка
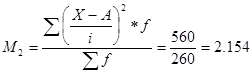
Тогда имеем средняя продолжительность работы станка:
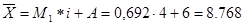 лет лет
Определим моду:
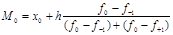 = =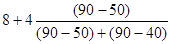 =9,78 лет. =9,78 лет.
Определим медиану:
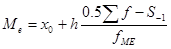 = =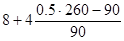 =12,77 лет =12,77 лет
Определим среднее линейное отклонение
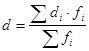 = =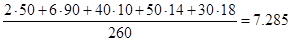
Дисперсия определим по формуле:
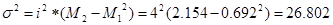
Среднее квадратическое отклонение определим по формуле:
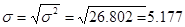
Коэффициент вариации:
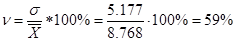
Так как коэффициент вариации больше 33%, значит ряд не устойчивый (совокупность не однородная).
Ответ: средняя длительность работы станка 8,768 лет; дисперсия – 26,802, среднее квадратическое отклонение – 5,177; коэффициент вариации -59%;
Задача 4.12
Имеются данные о производстве продукции промышленного предприятия за 1994–1999 гг. смотреть таблицу 7
Таблица 7
| Год |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
| Произведено млн. грн. |
8,0 |
8,4 |
8,9 |
9,5 |
10,1 |
10,8 |
Исчислите аналитические показатели ряда динамики продукции предприятия за 1994–1999 гг. абсолютное значение одного процента прироста, а также средние обобщающие показатели ряда динамики.
Решение
1) Абсолютный прирост базисный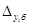 определяется по формуле: определяется по формуле:
Реклама

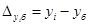 , ,
где 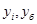 – уровни i‑го и базисного годов соответственно; – уровни i‑го и базисного годов соответственно;
Абсолютный прирост цепной (по годам) 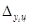 определяется по формуле: определяется по формуле:
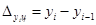 , ,
где 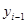 – уровень предыдущего года; – уровень предыдущего года;
Темп роста базисный 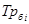 определяется по формуле: определяется по формуле:
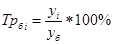 , ,
Темп роста цепной (по годам) 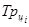 определяется по формуле: определяется по формуле:
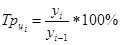
Темп прироста базисный 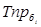 определяется по формуле: определяется по формуле:
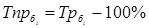
Темп прироста цепной (по годам) 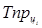 определяется по формуле: определяется по формуле:
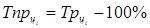
Абсолютное содержание одного процента прироста 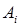 определяется по формуле: определяется по формуле:
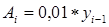
Рассчитаем по перечисленные величины и составим рабочую таблицу (см. таблица 8).
Таблица 8
| Год |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
| Произведено млн. грн. |
8 |
8,4 |
8,9 |
9,5 |
10,1 |
10,8 |
| Абсолютный прирост базисный |
- |
0,4 |
0,9 |
1,5 |
2,1 |
2,8 |
| Абсолютный прирост цепной (по годам) |
- |
0,4 |
0,5 |
0,6 |
0,6 |
0,7 |
| Темп роста базисный |
- |
105,00% |
111,25% |
118,75% |
126,25% |
135,00% |
| Темп роста цепной (по годам) |
- |
105,00% |
105,95% |
106,74% |
106,32% |
106,93% |
| Темп прироста базисный |
- |
5,00% |
11,25% |
18,75% |
26,25% |
35,00% |
| Темп прироста цепной (по годам) |
- |
5,00% |
5,95% |
6,74% |
6,32% |
6,93% |
| Абсолютное содержание 1‑го%-та прироста |
- |
0,08 |
0,084 |
0,089 |
0,095 |
0,101 |
Изобразим исходные данные графически (см. рисунок 2)
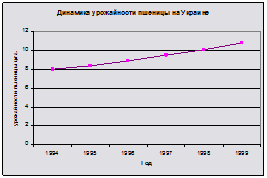
Рисунок 2 – Динамика производства продукции на предприятии с 1994 по 1999 год
Вывод: график показывает, что производство продукции на предприятии с 1994 г. по 1999 г. наблюдалась тенденция увеличения производства.
Задача 5.13
По городской телефонной сети из 1000 абонентов в порядке механической выборки произвели 100 наблюдений и установили, что средняя продолжительность телефонного разговора составляет 4 мин. При среднем квадратичном отклонении 2 мин.
Определите:
1. предельную ошибку репрезентативности (с вероятностью 0,954)
2. вероятность того, что предельная ошибка репрезантивности не превысила 0,3 мин.
Решение
1. Средняя ошибка среднего длительность звонка в выборке (выборочной средней)
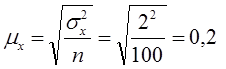
Предельная ошибка репрезентивности с вероятностью 0,954 (гарантийный коэффициент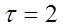 ) составит
) составит
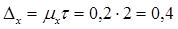
2. Определим вероятность того, что предельная ошибка репрезантивности не превысила 0,3 мин.
Необходимая численность выборки при вероятности 0,954 (гарантийный коэффициент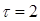 ) определяется следующим образом:
) определяется следующим образом:
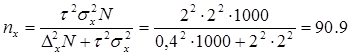 . .
Проверка.
предельная ошибка длительности телефонного звонка составляет
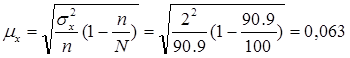 чел. чел.
Предельная ошибка выборочной средней при вероятности 0,954 (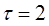 )
)
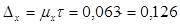 мин. не превышает заданной ошибки 0,3 мин. мин. не превышает заданной ошибки 0,3 мин.
Задача 6.16
Имеются данные о продаже товаров таблица 10
Таблица 10
| Товарные группы |
Продано товара в 2002 году млн. грн. |
Индексы количества товаров в 2003 г. По сравнению с 2002 г. |
| Ткани шерстяные |
45 |
0,97 |
| Трикотажные изделия |
54 |
1,12 |
| Обувь |
34 |
1,25 |
Вычислите общий индекс физического объема товарооборота в 2003 г. По сравнению с 2002 г.
Используя взаимосвязь индексов, определите, насколько процентов в среднем изменилась цена на проданные товары, если известно, что товарооборот в фактических ценах вырос на 10%
| Товарные группы |
Продано товара в 2002 году млн. грн. |
Индексы количества товаров в 2003 г. По сравнению с 2002 г. |
| Ткани шерстяные |
45 |
43,65 |
| Трикотажные изделия |
54 |
60,48 |
| Обувь |
34 |
42,5 |
Решение
1) Общий индекс физического объема товарооборота в 2003 г. по сравнению с 2002 г.
Общий индекс физического объема товарооборота вычисляется по формуле:
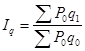 , ,
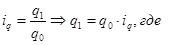 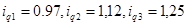 , тогда , тогда
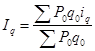 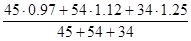 =1,112 (111,2%) =1,112 (111,2%)
Вывод:
индекс физического объема товарооборота в 2003 г. по сравнению с 2002 г. в отчетном периоде увеличился на 11,2%.
2) Используя взаимосвязь индексов, определите, насколько процентов в среднем изменилась цена на проданные товары, если известно, что товарооборот в фактических ценах вырос на 10%.
Общий индекс цен вычисляется по формуле:
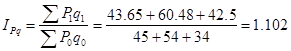 , ,
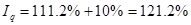 – изменение товарооборота в фактических ценах. – изменение товарооборота в фактических ценах.
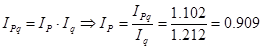 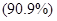
Вывод: при увеличении товарооборота на 10% проявляется тенденция снижения индекса цен на 9,1%
Список использованной литературы
1. Практикум по курсу «Статистика» для студентов всех специальностей. Часть 1 /Сост.: Акимова Е.В., Маркевич О.В. – Краматорск, ДГМА, 2002 – 59 с.
2. Практикум по курсу «Статистика» для студентов всех специальностей. Часть 2 /Сост.: Акимова Е.В., Маркевич О.В. – Краматорск, ДГМА, 2002 – 54 с.
3. Теория статистики: Учебник /Под ред. проф. Р.А. Шмойловой. – 3-е изд., перераб. – М.:
Финансы и статистика, 2002. – 560 с.: ил.
4. Практикум по теории статистики: Учеб. пособие /Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 2003. – 416 с.: ил.
|