Міністерство освіти і науки України
Національний технічний університет
“ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”
Кафедра “Обчислювальної техніки та програмування”
Реферат з курсу “
Введение в численные методы
”
Тема: “ПОИСК ОПТИМАЛЬНЫХ РЕШЕНИЙ”
Виконав:
студент групи
Перевірив:
Харків
Содержание
1. Основные понятия оптимизационных задач
2. Итерационные процессы с учетом градиента
3. Функционал для градиентного равенства
4. Функционалы в задачах условной оптимизации
Литература
1.
Основные понятия оптимизационных задач
К задачам поиска нулей функций сводятся многие задачи нахождения наибольших или наименьших значений многомерных функций в заданной области. В литературе такого рода задачи называются задачами оптимизации. В этих задачах дополнительно оговариваются условия, при которых оптимум должен быть достигнут. В качестве условий могут выступать системы алгебраических уравнений, или системы неравенств, или и то и другое одновременно. Оптимизируемая функция при этом является, как правило, критериальной, т.е. описывающей показатель качества объекта.
Простым примером оптимизационной задачи может быть метод наименьших квадратов (МНК), где критерием качества аппроксимации служила сумма квадратов отклонений заданной системы точек от искомой аппроксимирующей кривой. Аналогичным образом построенные многопараметрические критериальные выражения в литературе называют функционалами, минимуму которых и необходимо удовлетворить соответствующим выбором параметров функционала.
Если функционал построен, включает в себя параметры и не содержит ограничений или условий на характер и диапазон изменения параметров, то система уравнений относительно неизвестных значений параметров получается приравниванием частных производных по всем параметрам нулю. В результате задача оказывается сведенной к решению линейной, как в МНК, или в общем случае нелинейной системы уравнений. Такие задачи называются задачами безусловной оптимизации.
2.
Итерационные процессы с учетом градиента
Ограничения и условия в задачах оптимизации встраивают тем или иным образом в общий функционал, после чего решают задачу поиска экстремума. Наиболее популярной структурой функционала является взвешенная сумма квадратов невязок, полученных из условий и ограничений. Это обеспечивает всему функционалу квадратичную зависимость по каждому неизвестному параметру и, как следствие, локальный минимум всему функционалу.
Реклама

Изменение искомых параметров можно подчинить какой-либо детерминированной динамической процедуре, обеспечивающей сходимость итерационного процесса движения к точке минимума. Наиболее распространенным, имеющем множество модификаций, процессом является метод градиента: вектор скорости изменения неизвестных параметров пропорционален с обратным знаком вектору градиента функционала
:
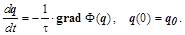
Это условие соответствует выбору наибольшей скорости убывания функционала, что несложно увидеть, рассмотрев выражение для производной функционала по времени:
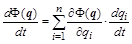 . .
Правую часть можно рассматривать как скалярное произведение двух n-
компонентных векторов: вектора градиента
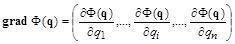
и вектора скорости изменения координат-параметров
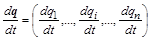 . .
Скалярное произведение максимально, когда векторы коллинеарные.
В результате система градиентных уравнений наискорейшего приближения к значениям оптимальных параметров приобретает вид:
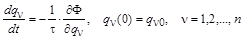 . .
Вид функционала существенно влияет на достижение локального минимума в итерационном процессе решения полученного градиентного уравнения. Численная итерационная процедура для решения последнего легко записывается, если производные правых частей системы представить конечными разностями первого порядка и переписать уравнения, разрешенными относительно очередных приближений искомых решений:
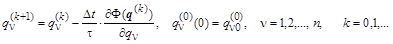
Равенство нулю градиента функционала может означать остановку итерационного процесса на одной из седловых точек, когда производные первого порядка по всем переменным 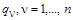 равны нулю, а некоторые из производных второго порядка имеют разные знаки по обе стороны от точки остановки решения. Это возможно, когда функция равны нулю, а некоторые из производных второго порядка имеют разные знаки по обе стороны от точки остановки решения. Это возможно, когда функция 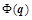 нелинейная. Чтобы сдвинуться с точки промежуточной остановки на пути к локальному минимуму, необходимо провести оценку знаков вторых смешанных производных по всем неизвестным. В общем виде, в случае многомерного нелинейного функционала, смешанные производные второго порядка могут быть представленными в векторной форме. Для этого в разложении Тейлора достаточно произвести перегруппировку частных производных так, чтобы группы слагаемых представляли скалярные произведения векторов и матриц из частных производных: нелинейная. Чтобы сдвинуться с точки промежуточной остановки на пути к локальному минимуму, необходимо провести оценку знаков вторых смешанных производных по всем неизвестным. В общем виде, в случае многомерного нелинейного функционала, смешанные производные второго порядка могут быть представленными в векторной форме. Для этого в разложении Тейлора достаточно произвести перегруппировку частных производных так, чтобы группы слагаемых представляли скалярные произведения векторов и матриц из частных производных:
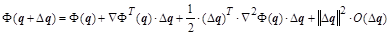 , ,
где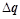 , ,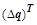 – вектор-столбец и вектор-строка очередных приращений, – вектор-столбец и вектор-строка очередных приращений,
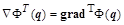 – строчная форма записи вектора градиента, – строчная форма записи вектора градиента,
Реклама

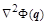 – матрица вторых частных производных (гессиан
), – матрица вторых частных производных (гессиан
),
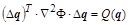 – квадратичная форма с матрицей Гессе, – квадратичная форма с матрицей Гессе,
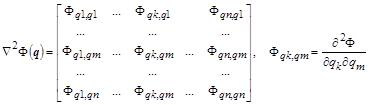 . .
Условием достижения локального минимума является положительная определенность квадратичной формы с матрицей Гессе 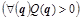 в точке остановки, в которой в точке остановки, в которой 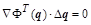 . Квадратичная форма положительна тогда и только тогда, когда все главные миноры ее квадратной матрицы, например, матрицы A
, положительны: . Квадратичная форма положительна тогда и только тогда, когда все главные миноры ее квадратной матрицы, например, матрицы A
, положительны:
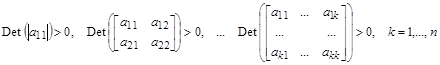 . .
Из проведенных рассмотрений можно сделать заключение, что для линейных функционалов любая остановка итерационного процесса соответствует локальному экстремуму, так как производные выше второй равны нулю.
3
. Функционал для градиентного равенства
Функционалом можно считать любую функцию, минимум которой необходимо определить. Вся сложность задачи заключается в ограничениях, накладываемых на переменные и их взаимосвязь. Если ограничения отсутствуют, то говорят о задаче безусловной оптимизации (Пример МНК). К последней сводится и система нелинейных алгебраических уравнений, заданных в неявной форме:
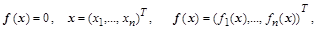
если из системы сконструировать квадратичный функционал такого вида
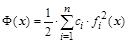 , ,
где 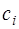 – масштабирующие (весовые) коэффициенты. – масштабирующие (весовые) коэффициенты.
Подстановка функционала в покомпонентную систему градиентных уравнений приводит к итерационной процедуре с вычислением на каждом шаге следующих выражений:
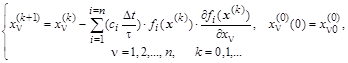
Если система уравнений линейная, то частные производные 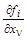 будут константами будут константами 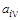 . Вместе с . Вместе с 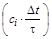 = =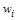 они определяют индивидуальный весовой коэффициент каждого уравнения исходной линейной системы в формулах градиентной итерационной процедуры. они определяют индивидуальный весовой коэффициент каждого уравнения исходной линейной системы в формулах градиентной итерационной процедуры.
Для нелинейной системы, функционал которой в окрестности точки минимума 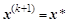 можно аппроксимировать квадратичной функцией с положительно определенной матрицей Гессе, в итерационном выражении можно аппроксимировать квадратичной функцией с положительно определенной матрицей Гессе, в итерационном выражении
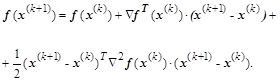
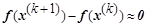 и после приравнивания оставшихся слагаемых нулю и сокращения суммы на вектор и после приравнивания оставшихся слагаемых нулю и сокращения суммы на вектор 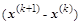 несложно получить соотношение несложно получить соотношение
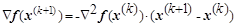 , ,
которое приводит к итерационной формуле
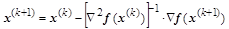
идентичной формуле Ньютона в применении к решению системы нелинейных уравнений
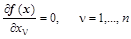 . .
Для строго выпуклой, квадратичной функции решение получается за одну итерацию. Этот момент особенно привлекателен для задач линейного программирования, когда целевая функция линейная или квадратичная, а ограничения представлены системой линейных равенств и неравенств. При этом системы равенств и неравенств вводят в общий функционал в виде суммы квадратов функций невязок (аддитивно).
4. Функционалы в задачах условной оптимизации
Конструирование выпуклого квадратичного функционала с учетом ограничений рассмотрим для следующей задачи:

В приведенную обобщенную запись задачи минимизации включены:
Минимизируемая функция вектора искомых параметров (функция цели или критериальная функция):
f
(x
),  . .
Система ограничений типа равенств:
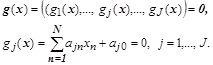
Система ограничений типа неравенств:
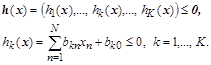
Ограничения на изменения самих неизвестных параметров
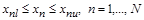 , ,
которые в принципе являются частным случаем ограничений типа неравенств 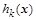 при при 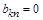 , кроме , кроме  и и 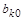 , задающего границы изменения конкретного параметра: , задающего границы изменения конкретного параметра:
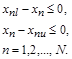
В качестве квадратов функций невязок для ограничений типа равенств берутся квадраты исходных равенств, умноженные на выравнивающие масштабирующие коэффициенты, которые позволят каждой невязке вносить в общий функционал одно-порядковые приращения при подстановке в него вектора неизвестных:
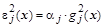 , j=
1, 2, ... ,J
. , j=
1, 2, ... ,J
.
Систему неравенств необходимо предварительно преобразовать в систему равенств путем умножения ее на единичную (знаковую) функцию
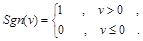
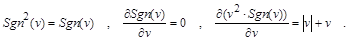
Теперь система квадратов невязок для неравенств будет представлена в виде квадратов следующих функций
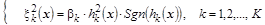 . .
Аналогично вводятся квадраты невязок и для ограничений на параметры снизу и сверху:
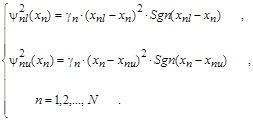
Составной функционал, учитывающий ограничения и требующий минимизации, можно теперь записать в следующем виде:
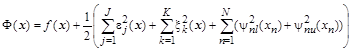 . .
В результате проведенных преобразований исходная задача сведена к задаче безусловной оптимизации и, применяя метод наискорейшего спуска, систему покомпонентных градиентных уравнений получим в виде:
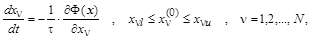
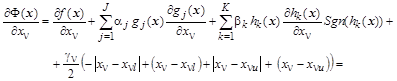
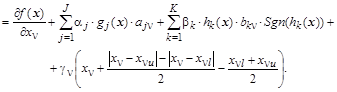
Выражение для 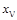 в больших круглых скобках задает кривую с зоной нечувствительности для в больших круглых скобках задает кривую с зоной нечувствительности для 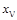 в интервале в интервале 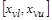 . В этом интервале выражение в скобках равно нулю, а вне интервала - пропорционально . В этом интервале выражение в скобках равно нулю, а вне интервала - пропорционально 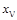 с коэффициентом с коэффициентом 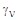 . Если ограничения на переменную не вводятся, т.е. ее границы раздвинуты от . Если ограничения на переменную не вводятся, т.е. ее границы раздвинуты от 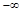 до до 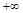 , то выражение в скобках будет равно нулю. , то выражение в скобках будет равно нулю.
Литература
1. Вержбицкий В.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М.: Высш.шк., 2001. - 383с.
2. Рено Н.Н. АЛГОРИТМЫ ЧИСЛЕННЫХ МЕТОДОВ: МЕТОДИЧЕСКОЕ ПОСОБИЕ ДЛЯ ВУЗОВ. Изд-во: "Книжный дом Университет" (КДУ), 2007. – 24с.
3. Самарский А.А. Введение в численные методы Учебное пособие для вузов 3-е изд.,стер. ЛАНЬ, 2005. – 288с.
4. Фаворский А.П., Костомаров Д.П. Вводные лекции по численным методам. Логос, 2006. – 184с.
5. Шуп Т.Е. Прикладные численные методы в физике и технике. М.: Высш. шк., 1990. - 255с.
|