Федеральное агентство по образованию
ГОУ ВПО Тульский государственный университет
Реферат
на тему: «Поверхности»
Дисциплина: «ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА»
Выполнил
студент группы 120691
Юдин А.С.
Проверил
Казимиров А.Н.
Поверхность - название для двумерного многообразия в пространстве.
Поверхности определяются как множество точек, координаты которых удовлетворяют определённому виду уравнений. Это неявный способ указания поверхности. Существуют еще два: явный способ (возможно, выразить одну переменную из уравнения поверхности через другие) и параметрический способ задания. При параметрическом указании задается система уравнений, которая и определяет поверхность.
Простая поверхность - поверхность, которую можно представить как часть плоскости, подвергнутую непрерывным искажениям.
Поверхности классифицируются по многим признакам. Некоторые из них:
1) Кривизна: каждому направлению поверхности от заданной точки соответствует своя форма сечения, которая и определяет кривизну;
2) Наличие касательной к поверхности: обычно касательная к поверхности – это плоскость. В некоторых случая через одну точку поверхности можно провести сколь угодно много касательных. Наличие касательной у какой-либо поверхности влияет на ее гладкость;
3) Метрика и внутренняя геометрия;
4) Нормаль: за нормаль к поверхности принимают единичный вектор, перпендикулярный касательной плоскости в заданной точке. Существует так же нормальное сечение;
5) Геодезические линии: кривая на поверхности называется геодезической линией, если во всех её точках главная нормаль к кривой совпадает с нормалью к поверхности;
6) Площадь: площадь в общем смысле – это числовая характеристика. Существуют поверхности с бесконечной площадью, например параболоид;
7) Ориентация: ориентированной называется двусторонняя поверхность с выбранным направлением нормали.
Приведем примеры некоторых поверхностей, опишем их основные характеристики, укажем применение и обозначение.
Эллипсоид
. Эллипсоидом называется поверхность, каноническое уравнение которой имеет вид
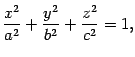
где a, b и c - положительные числа.
Данная поверхность обладает тремя плоскостями симметрии, тремя осями симметрии и центром симметрии. Ими служат соответственно координатные плоскости, координатные оси и начало координат. Существует так же эллипсоид вращения. Применяется в геодезии.
Реклама

Сфера
– частный случай эллипсоида - замкнутая поверхность, следовательно, она имеет конечную площадь. Площадь сферы находят по формуле S=4πR^2.
Поверхность обозначается формулой:
(x - x0)^2 + (y - y0)^2 + (z - z0)^2 = R^2.
Применяется во многих отраслях (например, шарики для подшипников)

Рис. 1
На рисунке 1 представлен тор
. Тор получается при вращении окружности радиуса b по окружности радиуса a. Существует возможность проведения такой касательной плоскости, которая будет иметь с тором только одну единственную точку. Обозначается параметрическими уравнениями:
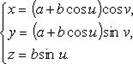
Применяется в хлебопекарной промышленности.
Рисунок 1 содержит катеноид
. Параметрическое уравнение:
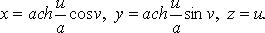
Эта поверхность применяется в медицинской технике, для создания излучателя ультразвуковых волн. Имеет бесконечную площадь, причем это поверхность вращения.
Псевдосфера и
меет следующее параметрическое уравнение:
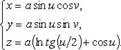
Существование псевдосферы выявлено из работ Лобачевского.
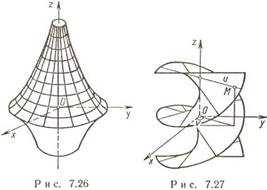
Рис. 2
На рисунке 2 изображен геликоид
. Прямой геликоид - поверхность, образованная движением прямой, вращающейся вокруг оси и перпендикулярной к ней и одновременно поступательно движущейся в направлении этой оси, причем скорости этих движений пропорциональны.
Задается параметрическими уравнениями:
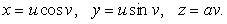
Применяется при создании винтовых поверхностей, например лестниц или валов мясорубок.
Параболоид
– поверхность вращения. Описывается уравнениями:
z = ax^2 + by^2
Одна из наиболее известных поверхностей – цилиндр
. Имеет параметрические уравнения вида:
x=cos2Ps;
y=2t-1;
z=sin2Ps.
Цилиндры имеют широчайшее применение во всех сферах жизни (например, колесо автомобиля, кружка, ручка).
Существует еще много поверхностей в пространстве, которые имеют необычную для нас форму и размер. Мы рассмотрели лишь простейшие из них.
|