Міністерство освіти і науки України
Кафедра вищої математики
КУРСОВА РОБОТА
з дисципліни
„Вища математика”
за темою:
Перетворення Фур’є. Спектри неперіодичних функцій.
Виконав студент групи
Викладач
Дніпропетровськ 2010
Атестаційний аркуш
захисту курсової роботи
студента_____________________________________________________
_____________________________________________________________
  Якість оформлення курсової роботи Якість оформлення курсової роботи
Якість виступу на захисті курсової роботи
  Рівень знань базового предмету Рівень знань базового предмету
Додаткові питання при захисті курсової роботи:
______________________________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
  Оцінка відповідей на додаткові питання Оцінка відповідей на додаткові питання
  КІНЦЕВА ОЦІНКА КІНЦЕВА ОЦІНКА
Дата захисту __________ 2010 р.
Підпис викладача _________________
Підписи комісії ____________________
Зміст
Вступ
1. Постановка задачі
2. Перетворення Фур'є
2.1 Зображення функції інтегралом Фур’є
2.2 Комплексна форма інтеграла Фур’є
2.3 Інтегральне перетворення Фур’є
3. Спектральна характеристика (щільність) неперіодичної функції
4. Розрахункова частина
Висновки
Список використаної літератури
Розкладання періодичної функції в ряд Фур'є з погляду фізики відповідає на запитання про розподіл енергії процесу по гармоніках, дискретно, тобто стрибком, що міняє частоту.
Такі явища, як світлові промені або шуми при радіозв'язку містять у своєму складі гармоніки всіх частот та у дану схему не укладаються. Безперервна зміна частоти приводить до поняття інтеграла Фур'є, у якому розподіл енергії по частотах характеризується спектральною щільністю. Кожній окремій узятій частоті відповідає нульова енергія, однак вона здобуває вагу, якщо розглядається деякий інтервал частот. Подібно повній масі, що у випадку безперервного розподілу виражається інтегралом від щільності, до інтеграла зводиться й повна енергія процесу, неперервно розподілена по частотах. Цей підхід став надбанням фізиків і інженерів, чиї професійні інтереси пов'язані з теорією передачі сигналів (радіофізика, оптика, акустика, кібернетика, електричні лінії тощо). Разом з тим, незалежно від фізичного змісту гармонійний аналіз має іншу важливу складову, він - ефективний засіб рішення широкого класу задач із різних галузей науки.
Реклама

Перетворення Фур'є - це самостійна операція математичного аналізу, досліджувана в курсовій роботі саме в цій якості.
Для неперіодичної функції 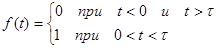 , знайти розклад інтеграла Фур'є амплітудний і фазовий спектри. , знайти розклад інтеграла Фур'є амплітудний і фазовий спектри.
Ця задача має відношення до розділу математики, який називають гармонійний аналіз (або Фур'є аналіз).
Спектральный аналіз (Spectral analysis, Синоніми: Фур'єАналіз, Гармонійний аналіз, Frequency analysis) - це різновид обробки даних, пов'язаний з перетворенням їхнього частотного подання або спектра. Спектр виходить у результаті розкладання вихідної функції, що залежить від часу (часовий ряд) або просторових координат (наприклад, зображення), у базис деякої періодичної функції. Найбільш часто для спектральної обробки використовується спектр Фур'є, одержуваний на основі базису синуса (розкладання Фур'є, перетворення Фур'є) [7].
Основний зміст перетворення Фур'є в тім, що вихідна неперіодична функція довільної форми, яку неможливо описати аналітично й у загальному випадку важка для обробки й аналізу, представляється у вигляді сукупності синусів або косинусів з різною частотою й амплітудою. Іншими словами, складна функція перетвориться в множину більш простих. Кожна синусоїда (або косинусоїда) з певною частотою й амплітудою, отримана в результаті розкладання Фур'є, називається спектральною складовою або гармонікою. Спектральні складові створюють спектр Фур'є [5].
Візуально спектр Фур'є представляється у вигляді графіка, на якому по горизонтальній осі відкладається кругова частота, позначувана грецькою буквою "омега", а по вертикалі - амплітуда спектральних складових, звичайно позначувана латинською буквою A. Тоді кожна спектральна складова може бути представлена у вигляді відліку, положення якого по горизонталі відповідає її частоті, а висота - її амплітуді. Гармоніка з нульовою частотою називається постійною складовою (у тимчасовому поданні це пряма лінія).
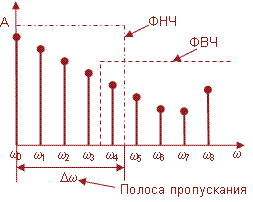
Рис.1.1 Основні показники спектру функції [7]
Навіть простий візуальний аналіз спектра може багато сказати про характер функції, на основі якої він був отриманий. Інтуїтивно зрозуміло, що швидкі зміни вихідних даних породжують у спектрі складові з високою частотою, а повільні - з низкою. Тому якщо в ньому амплітуда складових швидко убуває зі збільшенням частоти, то вихідна функція (наприклад, часовий ряд) є плавною. І, навпаки, якщо в спектрі присутні високочастотні складові з великою амплітудою, то вихідна функція буде містити різкі коливання. Так, для часового ряду це може вказувати на більшу випадкову складову, нестійкість описуваних їм процесів, наявність шумів у даних.
Реклама

В основі спектральної обробки лежить маніпулювання спектром. Дійсно, якщо зменшити (придушити) амплітуду високочастотних складових, а потім на основі зміненого спектра відновити вихідну функцію, виконавши зворотне перетворення Фур'є, то вона стане більш гладкою за рахунок видалення високочастотного компонента. Для часового ряду, наприклад, це означає забрати ін. - формацію про щоденні продажі, які сильно піддані випадковим факторам, і залишити більше стійкі тенденції, наприклад, сезонність. Можна, навпаки, придушити складові з низькою частотою, що дозволить забрати повільні зміни, а залишити тільки швидкі. У випадку часового ряду це буде означати придушення сезонного компонента.
Застосовуючи спектр таким чином, можна домагатися бажаної зміни вихідних даних. Найбільше часто використовується згладжування часових рядів шляхом видалення або зменшення амплітуди високочастотних складових у спектрі [7].
Для маніпуляцій зі спектрами використовуються фільтри - алгоритми, здатні управляти формою спектра, придушувати або підсилювати його складові. Головною властивістю будь-якого фільтра є його амплітудно-частотна характеристика (АЧХ), від форми якої залежить перетворення спектра. Якщо фільтр придушує тільки складові з низькою частотою, то він називається фільтр нижніх частот (ФНЧ), і з його допомогою можна згладжувати дані, очищати їх від шуму й аномальних значень, а якщо тільки складові з високою частотою, то це фільтр високих частот (ФВЧ). Завдяки йому можна придушувати повільні зміни, наприклад, сезонність у рядах даних. Крім цього, використовується множина інших типів фільтрів: фільтри середніх частот, загороджувальні фільтри й смугові фільтри, а також більш складні, які застосовуються при обробці сигналів у радіоелектроніці. Підбираючи тип і форму частотної характеристики фільтра, можна домогтися бажаного перетворення вихідних даних шляхом спектральної обробки.
Виконуючи частотну фільтрацію даних з метою згладжування й очищення від шуму, необхідно правильно вказати смугу пропущення ФНЧ. Якщо її вибрати занадто великою, то ступінь згладжування буде недостатнім, а шум буде подавлений не повністю. Якщо вона буде занадто вузькою, то разом із шумом можуть виявитися подавленими й зміни, що несуть корисну інформацію.
Спектральний аналіз є одним з найбільш ефективних і добре розроблених методів обробки даних. Частотна фільтрація - тільки один з його численних додатків. Крім цього, він використовується в кореляційному й статистичному аналізі, синтезі сигналів і функцій, побудові моделей і т.д.
Наведемо лише суттєвими рисами ті міркування, що приводять до інтегральної формули Фур’ є [3].
Нехай функція 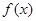 визначена на всій числовій прямій та задовольняє таким умовам: визначена на всій числовій прямій та задовольняє таким умовам:
Функція 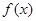 є обмеженою та абсолютно інтегрованою на є обмеженою та абсолютно інтегрованою на 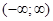 , тобто існує невластний інтеграл , тобто існує невластний інтеграл
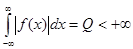
2. У будь-якому скінченому проміжку 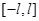 функція функція 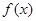 розкладається у ряд Фур’ є розкладається у ряд Фур’ є
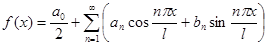 (2.1) (2.1)
де коефіцієнти Фур’є визначаються формулами
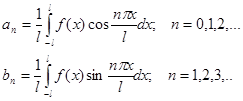 (2.2) (2.2)
Підставивши замість коефіцієнтів 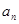 і і 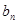 їх вирази, перепишемо ряд у вигляді їх вирази, перепишемо ряд у вигляді
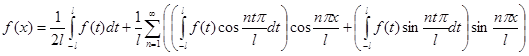
або
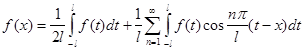 (2.3) (2.3)
Дістанемо граничну форму цього розвинення при 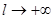 . Оскільки функція . Оскільки функція 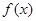 абсолютна інтегрована на всій числовій осі, то при граничному переході при абсолютна інтегрована на всій числовій осі, то при граничному переході при 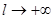 перший доданок у правій частині (2.3) прямує до нуля перший доданок у правій частині (2.3) прямує до нуля
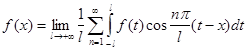 (2.4) (2.4)
Позначимо 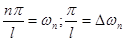 та перепишемо (2.4) як та перепишемо (2.4) як
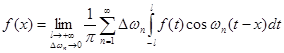 (2.5) (2.5)
При 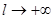 інтеграл інтеграл 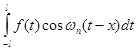 можна замінити інтегралом можна замінити інтегралом
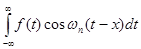 , а суму , а суму
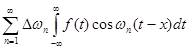
можна вважати за інтегральну суму для інтеграла
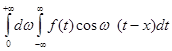
Таким чином, з рівності (2.5) дістаємо
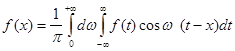 (2.6) (2.6)
Рівність (2.6) називається інтегральною формулою Фур’є, а інтеграл у її правій частині - інтегралом Фур’є. Зображення функції 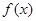 у вигляді інтеграла Фур’є звичайно називають розкладанням цієї функції в інтеграл Фур’є. у вигляді інтеграла Фур’є звичайно називають розкладанням цієї функції в інтеграл Фур’є.
Зауваження 1. Формула (2.6) має сенс тільки для точок неперервності функції 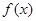 , а у кожній точці , а у кожній точці 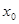 розриву першого роду, як і для рядів Фур’ є, інтеграл Фур’є збігається до числа розриву першого роду, як і для рядів Фур’ є, інтеграл Фур’є збігається до числа
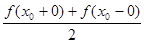 . .
Формулу (2.6) приводимо до вигляду, що є збіжним з рядом Фур’ є:
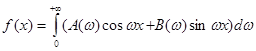 (2.7) де (2.7) де
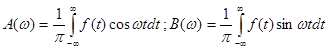 (2.8) (2.8)
Рівність (2.7) аналогічна розвиненню функції в тригонометричний ряд Фур’є, а вираз (2.8) - формулам для коефіцієнтів Фур’ є. І, таким чином, (2.7) можна трактувати як розкладання неперіодичної функції, визначеної на всій числовій осі на суму гармонічних складових частоти 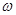 , які неперервно заповнюють дійсну піввісь , які неперервно заповнюють дійсну піввісь 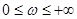
Зауваження 2. Якщо функція 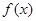 - парна, то - парна, то 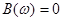 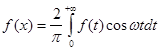 та інтеграл Фур’є для такої функції має вигляд та інтеграл Фур’є для такої функції має вигляд
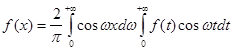 (2.9) (2.9)
У випадку непарної функції 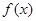
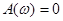 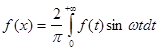
інтеграл Фур’є набуває вигляду
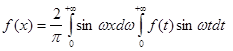 (2.10) (2.10)
Приклад 1. Зобразити інтегралом Фур’є неперіодичну функцію
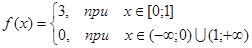

Дана функція задовольняє умовам зображення її інтегралом Фур’є. За формулами (2.8) і (2.7)
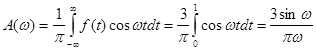
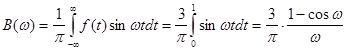
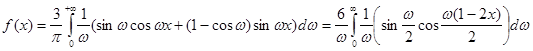
у точках розриву 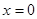 і і 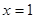 інтеграл збігається до числа інтеграл збігається до числа 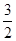
Приклад 2. Зобразити інтегралом Фур’є неперіодичну функцію
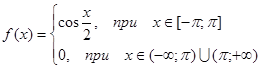
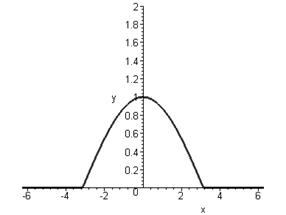
Функція задовольняє умовам зображення її інтегралом Фур’ є, до того ж вона парна, а відтак 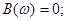
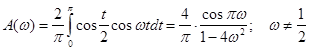
Якщо 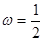 , то , то
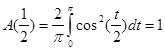 і і
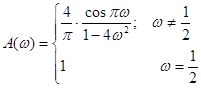
Функція 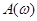 у точці у точці 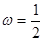 має усувний розрив (що не впливає на значення інтеграла (2.7)). Побудоване зображення функції має усувний розрив (що не впливає на значення інтеграла (2.7)). Побудоване зображення функції 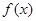 інтегралом Фур’є можна записати у вигляді інтегралом Фур’є можна записати у вигляді
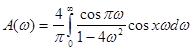 . .
Перетворимо за допомогою формули Ейлера [2] підінтегральну функцію у формулі (2.7) до наступного вигляду
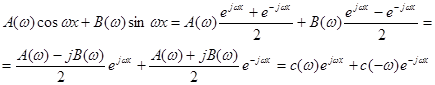 (2.11) (2.11)
де позначено
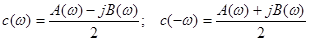
Тоді
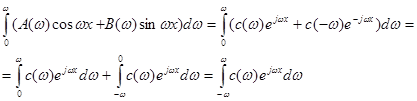 (2.12) (2.12)
Для 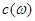 дістаємо вираз дістаємо вираз
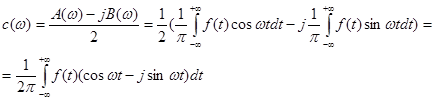 (2.13) (2.13)
Звідси
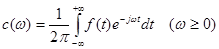 (2.14) (2.14)
Безпосередньо бачимо, що ці формули не втрачають сенс і при 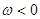 , бо , бо 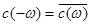 . Тому із формули (2.7) випливає . Тому із формули (2.7) випливає
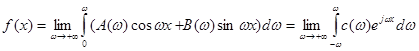 (2.15) (2.15)
Отже, в точках неперервності функції
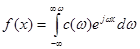 (2.16) де (2.16) де
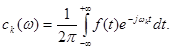 (2.17) (2.17)
Вираз для 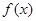 у формі (2.15) називають комплексною формою інтеграла Фур’є для функції у формі (2.15) називають комплексною формою інтеграла Фур’є для функції 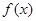 . .
Зауваження. Множник 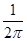 можна записати у будь - яку з формул (2.16) чи (2.17): у вираз для можна записати у будь - яку з формул (2.16) чи (2.17): у вираз для 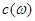 , як у формулі (2.17), або у формулі (2.16), як це у подальшому буде зроблено для формул перетворення Фур’ є відповідно до стандартів електротехніки. , як у формулі (2.17), або у формулі (2.16), як це у подальшому буде зроблено для формул перетворення Фур’ є відповідно до стандартів електротехніки.
Приклад. Побудувати розклад (2.17) для функції
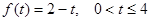 , , 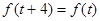
Розв‘язок
Тут 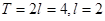 . Проінтегруємо по проміжку . Проінтегруємо по проміжку 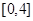 , відповідно (2.2) при , відповідно (2.2) при 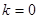 отримаємо отримаємо
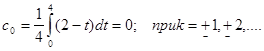

Оскільки
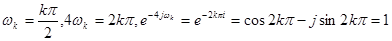 , тоді , тоді
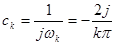 . .
Розклад (2.18), де 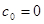 запишеться як: запишеться як:
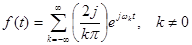
При дотриманні певних умов у ряд Фур'є розкладається періодична функція, задана на всій дійсній осі, або функція, визначена на кінцевому інтервалі. Розкладання в ряд Фур'є неперіодичної функції, заданої на необмеженому інтервалі, нездійсненно. Однак ідея подання функції нескінченним набором гармонік у декілька зміненій формі реалізована і в цьому випадку. Засобом досягнення мети служить інтеграл Фур'є [3], [4], [5].
Припустимо, що комплексна формула інтеграла Фур'є має місце для всіх значень 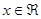 за винятком скінченої кількості точок. за винятком скінченої кількості точок.
Тоді
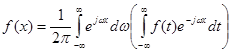 (2.18) (2.18)
Вираз у дужках - функція від 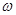 . Позначимо цю функцію . Позначимо цю функцію 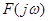 : :
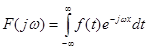 (2.19) тоді (2.19) тоді
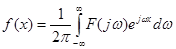 (2.20) (2.20)
Вирази (2.19) та (2.20) називаються двобічним прямим та оберненим перетворенням Фур'є. Якщо функція 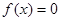 при при 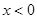 , то дістанемо однобічні перетворення Фур'є. , то дістанемо однобічні перетворення Фур'є.
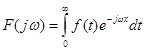 (2.21) (2.21)
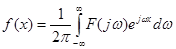 (2.22) (2.22)
Аналогічно, звернувшись до формул (2.9) і (2.10), можна ввести пряме і обернене косинус-перетворення Фур'є для парної функції 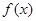 . .
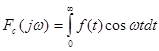 (2.23) (2.23)
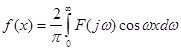 (2.24) (2.24)
та пряме і обернене синус-перетворення Фур'є для непарної функції 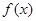 : :
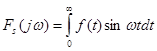 (2.25) (2.25)
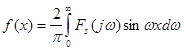 (2.26) (2.26)
Приклад. Знайти прямі косинус - перетворення Фур'є 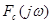 та синус-перетворення та синус-перетворення 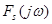 функції функції 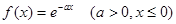 . .
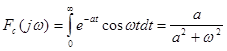 , , 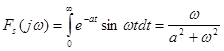
За формулами обернених перетворень (2.24) і (2.25) маємо
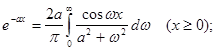
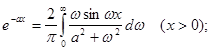
У відповідності з формулою (2.22), неперіодична функція 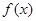 зображується сукупністю нескінченно великої кількості гармонік з нескінченно малими амплітудами зображується сукупністю нескінченно великої кількості гармонік з нескінченно малими амплітудами 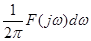 у всьому діапазоні частот у всьому діапазоні частот 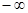 до до 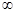 . Функцію . Функцію 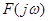 , визначену для неперіодичної функції , визначену для неперіодичної функції 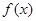 за формулою (2.19) чи (2.22), називають спектральною характеристикою (спектральною щільністю, спектральною функцією) функції за формулою (2.19) чи (2.22), називають спектральною характеристикою (спектральною щільністю, спектральною функцією) функції 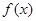 . ЇЇ модуль . ЇЇ модуль 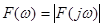 і аргумент і аргумент 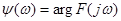 називають відповідно амплітудною та фазовою спектральними характеристиками (відповідно амплітудно-частотним та фазочастотним спектрами). називають відповідно амплітудною та фазовою спектральними характеристиками (відповідно амплітудно-частотним та фазочастотним спектрами).
Деякі властивості спектральної характеристики. Нехай 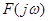 - спектральна характеристика - спектральна характеристика 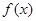 (це символічно можна записати (це символічно можна записати 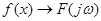 . Тоді спектральній характеристиці (у випадку двобічного перетворення Фур'є) притаманні такі властивості [3]: . Тоді спектральній характеристиці (у випадку двобічного перетворення Фур'є) притаманні такі властивості [3]:
Лінійність 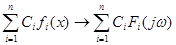 де де 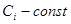 ; ; 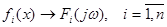
Диференціювання оригіналу 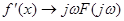 , якщо , якщо 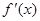 абсолютно інтегрована функція. Інтегрування оригіналу абсолютно інтегрована функція. Інтегрування оригіналу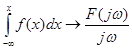 за умови, що за умови, що 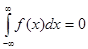 . Диференціювання спектральної функції . Диференціювання спектральної функції 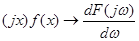 у випадку, коли у випадку, коли 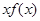 - абсолютно інтегрована функція - абсолютно інтегрована функція
Зміна масштабу незалежної змінної 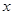 . . 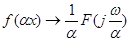
Зсув незалежної змінної 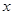 . . 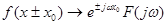
Зсув спектральної функції 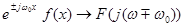
Множення функції 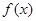 на косинус та синус на косинус та синус
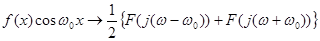
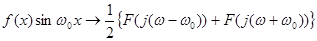
Функція 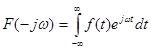 - комплексно - спряжена для функції - комплексно - спряжена для функції 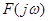 , і, оскільки модулі спряжених функцій , і, оскільки модулі спряжених функцій 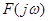 і і 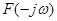 рівні, а аргументи - відрізняються знаком, то амплітудно-частотний спектр - завжди парна, а фазо-частотний спектр - завжди непарна функція частоти рівні, а аргументи - відрізняються знаком, то амплітудно-частотний спектр - завжди парна, а фазо-частотний спектр - завжди непарна функція частоти 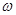 . .
Інколи спектральну характеристику 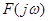 описують кривими, що являють собою дійсну описують кривими, що являють собою дійсну 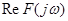 та уявну та уявну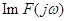 частину спектральної функції. частину спектральної функції.
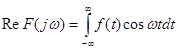 (3.1) (3.1)
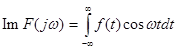 (3.2) (3.2)
Ці дві криві містять повну інформацію про амплітуду і фазу спектральної характеристики причому 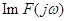 - непарна функція, - непарна функція, 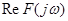 - парна функція, а відтак, якщо функція - парна функція, а відтак, якщо функція 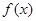 - парна, то спектр зводиться тільки до дійсної частини - парна, то спектр зводиться тільки до дійсної частини 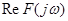 , що збігається з , що збігається з 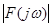 . Аналогічно у разі непарної функції . Аналогічно у разі непарної функції 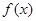 спектр зводиться до уявної частини спектр зводиться до уявної частини 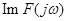 . .
Зауваження 1. Спектральну характеристику можна вважати обвідною коефіцієнтів ряду Фур'є, тобто границею лінійчатого спектра частот періодичної функції, коли період функції прагне до нескінченності.
У розрахунковій частині даної роботи досліджується неперіодична функція
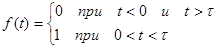 , ,
Потрібно знайти:
розклад в інтеграл Фур'є
амплітудний і фазовий спектр.
Розв'язання
а) Функція 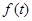 задовольняє таким умовам теореми Фур’є [4], [5]: задовольняє таким умовам теореми Фур’є [4], [5]:
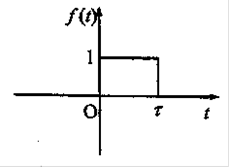
Рис.4.1 Графік досліджуємої неперіодичної функції f (t)
(прямокутний імпульс тривалості t) задана на всій осі 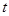 . на будь-якому кінцевому відрізку цієї осі задовольняє умовам Дирихле [], а отже розкладається в ряд Фур'є. . на будь-якому кінцевому відрізку цієї осі задовольняє умовам Дирихле [], а отже розкладається в ряд Фур'є.
Абсолютно інтегрувальна по всій осі, тобто 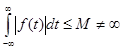 те функція те функція 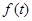 допускає подання у формі інтеграла Фур'є допускає подання у формі інтеграла Фур'є
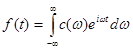 (4.1), де (4.1), де
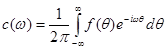 (4.2) (4.2)
Застосувавши (4.2), знайдемо спектральну щільність
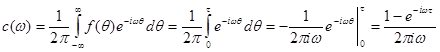 . (4.3) . (4.3)
Згідно (4.1), підставляючи (4.3), отримуємо інтеграл Фур’є в комплексній формі:
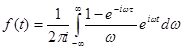 (4.4) (4.4)
З формули (4.4) після відділення дійсної й мнимої частини можна перейти до інтеграла Фур'є в дійсній формі. З обліком парних і непарних функцій одержимо
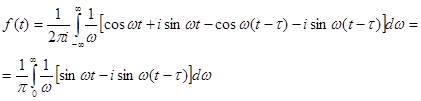 , тобто , тобто
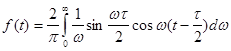 (4.5) (4.5)
б) Минаючи стандартну процедуру, визначимо модуль і аргумент величини 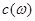 привівши її до показової форми запису привівши її до показової форми запису
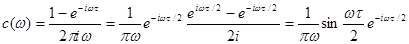 (4.6) (4.6)
Поки співмножник експоненти (разом із синусом) міняє знак, він не може відігравати роль модуля 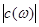 . Неважко перевірити, що в проміжках . Неважко перевірити, що в проміжках
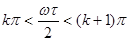 при при 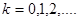
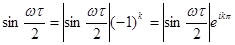 . .
Тому для 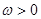 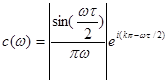 , значить , значить 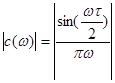 ; ;
звідки
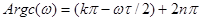 . (4.7) . (4.7)
В виразі (4.7) ціле число 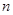 довільне, його варто вибрати так, щоб виділялося головне значення. Оскільки в означених вище інтервалах зміни w справедливо довільне, його варто вибрати так, щоб виділялося головне значення. Оскільки в означених вище інтервалах зміни w справедливо 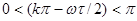 , то досить взяти , то досить взяти 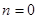 . .
Маємо:
1. амплітудний спектр у вигляді функції
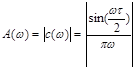 , ,
Побудуємо таблицю амплітудного спектра
Графік амплітудного спектра наведений на рис.4.2
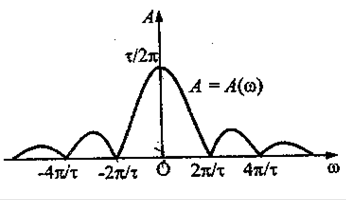
Рис.4.2 Графік амплітудного спектру досліджуємої неперіодичної функції
2. фазовий спектр у вигляді функції
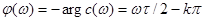 , , 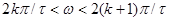 . Діаграми для . Діаграми для
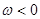 побудовані з урахуванням парності побудовані з урахуванням парності 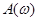 й непарності й непарності 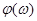 . .
Побудуємо таблицю для фазового спектра
Графік фазового спектра наведений на рис.4.3
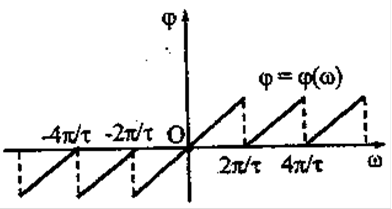
Рис.4.3 Графік фазового спектру досліджуємої неперіодичної функції
Розглянуту функцію 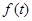 в радіотехніці застосовують для опису прямокутного імпульсу тривалості в радіотехніці застосовують для опису прямокутного імпульсу тривалості 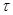 . Прилад, що реєструє цей сигнал, сприймає тільки кінцевий інтервал частот. Важливо, щоб в останній попадала основна частина спектра, який відповідає найбільшим значенням амплітуд . Прилад, що реєструє цей сигнал, сприймає тільки кінцевий інтервал частот. Важливо, щоб в останній попадала основна частина спектра, який відповідає найбільшим значенням амплітуд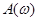 . Довжину такого інтервалу характеризують за допомогою поняття ширини спектра. У даному прикладі шириною спектра називають величину . Довжину такого інтервалу характеризують за допомогою поняття ширини спектра. У даному прикладі шириною спектра називають величину 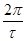 . Тривалість імпульсу . Тривалість імпульсу 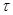 й ширина його спектра обернено залежні. Ця властивість - загальна для імпульсів різної форми. й ширина його спектра обернено залежні. Ця властивість - загальна для імпульсів різної форми.
В курсовій роботі розглянута теорія та практика спектрального аналізу функцій при спектральному представленні неперіодичних функцій з застосуванням математичного апарату інтегральних перетворень Фур’є.
Від періодичного коливання до неперіодичного можна просто перейти, якщо не змінюючи форми імпульсу безмежно збільшувати період його проходження, що, у свою чергу, приведе до нескінченно близького розташування друг до друга спектральних складових, а значення їхніх амплітуд стають нескінченно малими. Однак початкові фази цих складових такі, що сума нескінченно великої кількості гармонійних коливань нескінченно малих амплітуд відрізняється від нуля й дорівнює функції тільки там, де існує імпульс. Тому поняття спектра амплітуд для неперіодичного коливання не має змісту, і його заміняють, використовуючи пряме й зворотне перетворення Фур'є. Відомо, що функція, що задовольняє заданим умовам, може бути представлена інтегралом Фур'є (зворотне перетворення Фур'є)
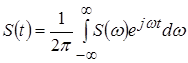 . .
Використовуючи пряме перетворення Фур'є, приходимо до інтеграла
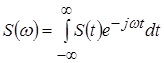 . .
Функція 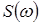 називається комплексною спектральною щільністю амплітуд, а її модуль називається комплексною спектральною щільністю амплітуд, а її модуль 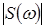 - спектральною щільністю амплітуд. Аргумент - спектральною щільністю амплітуд. Аргумент 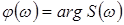 називають фазовим спектром неперіодичного коливання. називають фазовим спектром неперіодичного коливання.
1. Ильн В.А., Позняк Э.Г. Основы математического анализа. ч.1М.: "Наука" - 387с-1980. ч.2М. Наука. - 444с-1982.
2. Овчинников П.П. Вища математика: підручник. Ч.2-3є вид. - К.: Техніка, 2001. - 792 с.
3. 3. Поляков М.Г., Фомичова Л.Я., Сушко С.О., Математичні основи теоретичної електротехніки: Навчальний посібник - Дн.: НГА України, 2001. - ч.1-210с.
4. 4. Синайский, Е.С. Высшая математика: учеб. пособие. - 2е изд. - / Синайский Е.С., Новикова Л.В., Заславская Л.И.; Министерство образования и науки Украины, Национальный горный университет. - Днепропетровск: НГУ. - Ч.1. - 2009. - 399 с.
5. Синайский Е.С. Высшая математика / Синайский Е.С., Новикова Л.В., Заславская Л. И.; Министерство образования и науки Украины, Национальный горный университет. - Днепропетровск: НГУ. - Ч.2. - 2006. - 452 с.
6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. - М.: „Наука”, 1970. - Т.2. - 800 с.
7. Харкевич А.А. Спектры и анализ - М.: Физматгиз, 1980. - 246 с.
|