Методы решения алгебраических уравнений
1. Одношаговые итерационные модели
Для решения уравнений часто прибегают к итерационным методам, которые иногда называют методами последовательных приближений.
Суть этого класса методов можно раскрыть на примере.
Пусть нам нужно решить уравнение:
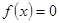 (1) (1)
для решения этого уравнения строится соответствующая итерационная формула:
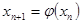 (2) (2)
Задавая начальное приближение корня уравнения (1) в виде:
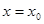 (3) (3)
находим дальнейшие приближения по формуле (2):
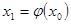 (4), (4), 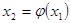 (5), (5), 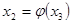 (6) (6)
Мы видим, что каждое вычисленное значение 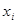 становится исходным для вычисления последующих приближений становится исходным для вычисления последующих приближений 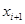 . .
Такие итерационные формулы называются одношаговыми.
Существуют и двухшаговые, трёхшаговые и т.д. итерационные формулы, которые определяются соответственно формулами:
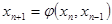
- двухшаговая формула (7)
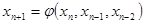
- трёхшаговые формула (8)
и т.д.
После построения итерационной формулы (2) возникают вопросы:
а) сколько нужно считать последовательных приближений 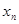 , т.е. когда остановиться? , т.е. когда остановиться?
б) сходится ли последовательность приближений 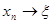 к корню к корню 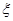 ? ?
Ответы на эти вопросы нужно давать всегда, когда имеем дело с методом последовательных приближений Пикара. На вопросы отвечают следующим образом:
а) задаётся точность вычислений 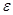 и итерационный процесс останавливают, как только достигается соответствующая абсолютная погрешность, т.е. как только выполняется условие: и итерационный процесс останавливают, как только достигается соответствующая абсолютная погрешность, т.е. как только выполняется условие:
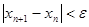 (9) (9)
б) нужно соответствующим образом строить формулы (2), используя соответствующие теоремы о достаточном условии сходимости. В частности теорему Банаха о сжатых отображениях.
Определение: Пусть M- метрическое пространство с метрикой 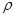 . Оператор A, отображающий это пространство в себя называется сжимающим, если существует такое число . Оператор A, отображающий это пространство в себя называется сжимающим, если существует такое число 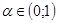 , что для любой пары элементов , что для любой пары элементов 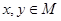 имеет место неравенство: имеет место неравенство:
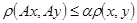 (10) (10)
Т.о. сжимающий оператор сжимает расстояние между элементами 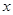 и и 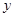 , т.е. расстояние между образами элементов , т.е. расстояние между образами элементов 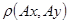 меньше или равно расстоянию между их прообразами меньше или равно расстоянию между их прообразами 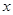 и и 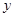 . Для таких отображений используется теорема Банаха. Теорема Банаха: Пусть A- сжимающий оператор в полном метрическом пространстве M, тогда уравнение . Для таких отображений используется теорема Банаха. Теорема Банаха: Пусть A- сжимающий оператор в полном метрическом пространстве M, тогда уравнение
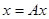 (11) (11)
имеет в этом пространстве одно и только одно решение, т.е. существует ровно один элемент 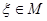 , для которого выполняется уравнение , для которого выполняется уравнение 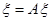 . Этот элемент может быть получен как предел последовательности элементов . Этот элемент может быть получен как предел последовательности элементов 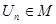
Реклама

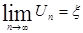 (12) (12)
где 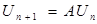 , причём элемент , причём элемент 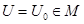 может быть выбран произвольно. Эта теорема применима и для случая, когда оператор может быть выбран произвольно. Эта теорема применима и для случая, когда оператор 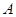 - является функцией, т.е. для формулы (2), а также для построения сходящихся итерационных формул Ритца-Якоби в случае линейных систем алгебраических уравнений с плохо обусловленной матрицей (определитель близок к нулю) коэффициентов, для дифференциальных и интегральных операторов и т.д. Для итерационной формулы (2), применяя формулу Лагранжа о конечных приращениях, получаем, что для - является функцией, т.е. для формулы (2), а также для построения сходящихся итерационных формул Ритца-Якоби в случае линейных систем алгебраических уравнений с плохо обусловленной матрицей (определитель близок к нулю) коэффициентов, для дифференциальных и интегральных операторов и т.д. Для итерационной формулы (2), применяя формулу Лагранжа о конечных приращениях, получаем, что для 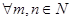 имеет место соотношение: имеет место соотношение:
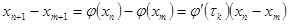 (13) (13)
что со своей стороны можно переписать в виде
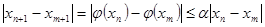 (14) (14)
если Чебышевская норма функций 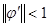 , т.е. если , т.е. если
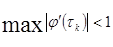 (15) (15)
В таком случае отображение 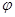 из (2) является сжимающим и, соответственно, для неё имеет место теорема Банаха.Т. е. итерационная формула (2) позволяет найти корень из (2) является сжимающим и, соответственно, для неё имеет место теорема Банаха.Т. е. итерационная формула (2) позволяет найти корень 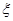 уравнения (1) по формуле уравнения (1) по формуле
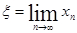 (16) (16)
Несмотря на кажущуюся простоту, итерационные формулы вида (2) таят в себе много интересных эффектов. Для раскрытия некоторых из них рассмотрим простейшую нелинейную итерационную формулу, возникающую в задаче об эволюции денежных вкладов.
2. Возникновение хаоса в детерминированных системах
Пусть 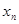 - количество денежных вкладов за - количество денежных вкладов за 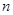 лет. Коэффициент относительного прироста вкладов обозначим через лет. Коэффициент относительного прироста вкладов обозначим через 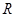 . Тогда имеем: . Тогда имеем:
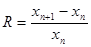 (17) (17)
т.е. 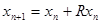 , где , где 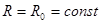 (18) (18)
Для исследования динамики процесса перепишем (18) в виде:
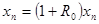 (19) (19)
Ясно, что если начальное значение денежного вклада было 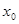 , тогда , тогда
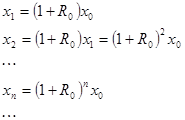 (20) (20)
из (20) следует, что с ростом n, количество денежных вкладов неограниченно увеличивается, т.к 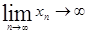 . .
Формула (20) позволяет решить задачу о допустимых процентах роста R. Например, выясним, каким должен быть R, чтобы удвоение вкладов происходило за 50 лет. Имеем:
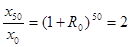 (21) (21)
Тогда
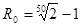 (22) (22)
т.е.
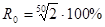 (23) (23)
Теперь допустим, что совет директоров банка решил увеличить коэффициент прироста R- для привлечения клиентов, но чтобы защитить себя от банкротства решил не допускать дальнейшего увеличения вкладов если величина достигает значения 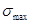 , после чего коэффициент должен становится отрицательным, т.е. уменьшать вклады пока не опустятся ниже , после чего коэффициент должен становится отрицательным, т.е. уменьшать вклады пока не опустятся ниже 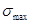 , для этого решили, что , для этого решили, что 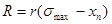 . Тогда из (17) получаем: . Тогда из (17) получаем:
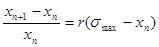 (24) (24)
где 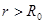 . Тогда имеем: . Тогда имеем:
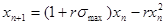 (25) (25)
Исследуем точки равновесия системы (25), т.е. те значения вкладов 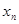 , которые с ростом n, не изменяются (или иначе , которые с ростом n, не изменяются (или иначе 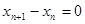 ). ).
Очевидно, что такими значениями служат:
а) 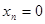 и б) и б) 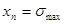 . .
Для того, чтобы точка равновесия реализовалась на практике нужна её устойчивость, иначе малое возмущение может её быстро вывести из состояния, так что мы и ахнуть не успеем. Поэтому, исследуем эти состояния на устойчивость.
Реклама

а) Рассмотрим сначала состояние равновесия 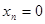 , т.е. состояние, когда на вашем счету денег нет.д.обавим малое "возмущение" точке равновесия , т.е. состояние, когда на вашем счету денег нет.д.обавим малое "возмущение" точке равновесия 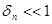 и исследуем её динамику со временем: т.е. и исследуем её динамику со временем: т.е. 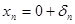 , тогда из (25) получаем: , тогда из (25) получаем:
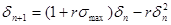 (27) (27)
т.к 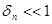 , ясно, что , ясно, что 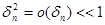 поэтому ею можно пренебречь в (27). Вследствии имеем: поэтому ею можно пренебречь в (27). Вследствии имеем:
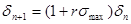 (29) (29)
отсюда, легко получить, что
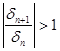 (29) (29)
т.е. возмущения нарастают со временем, что со своей стороны означает неустойчивость точки равновесия 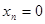 . По смыслу же, задачи это означает рост вклада со временем, если хоть какая-то малая сумма денег . По смыслу же, задачи это означает рост вклада со временем, если хоть какая-то малая сумма денег 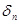 села на счёт. села на счёт.
б) Исследуем теперь устойчивость второй точки равновесия: 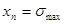 . Здесь также дадим малое приращение . Здесь также дадим малое приращение 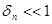 к точке равновесия, т.е. рассмотрим значение к точке равновесия, т.е. рассмотрим значение 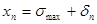 и исследуем динамику этого состояния с течением времени n. Из (25) получаем: и исследуем динамику этого состояния с течением времени n. Из (25) получаем:
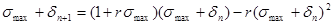 (30) (30)
Произведя преобразования, имеем:
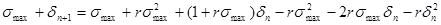
Учитывая, что 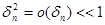 и поэтому, пренебрегая ею получаем: и поэтому, пренебрегая ею получаем:
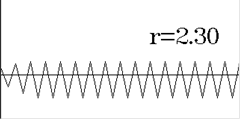
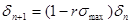 (31) (31)
для устойчивости точки равновесия 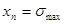 , должно выполнятся условие: , должно выполнятся условие:
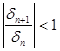 (32) (32)
т.е.
(рис.1)
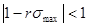 (33) (33)
это условие со своей стороны означает, что
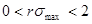 (34) (34)
таким образом, если мы выберем в качестве относительного коэффициента роста:

(рис.2)
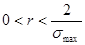 (35) (35)
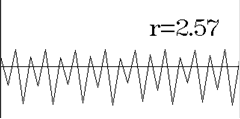
то состояние 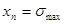 будет устойчивым, иначе мы вступаем в зону неустойчивостей, которая полна неожиданностями. В частности, при будет устойчивым, иначе мы вступаем в зону неустойчивостей, которая полна неожиданностями. В частности, при 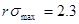 , (рис.3) возникают периодические колебания , (рис.3) возникают периодические колебания 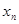 (рис.1). При (рис.1). При 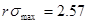 картина усложняется и появляется двоякопериодические колебания (рис.2) При дальнейшем росте относительного коэффициента прироста, получаем учетверение периода и т.д., в случае картина усложняется и появляется двоякопериодические колебания (рис.2) При дальнейшем росте относительного коэффициента прироста, получаем учетверение периода и т.д., в случае 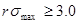 наблюдаются хаотические колебания (рис.3). наблюдаются хаотические колебания (рис.3).
Таким образом, нелинейные итерационные формулы типа (2) скрывают в себе множество тайн и для их раскрытия нужны дополнительные исследования в каждом конкретном случае. Тем более, что не всегда удаётся оценить сходимость итерационного процесса глобально.
Этот пример хоть и является частным случаем формулы (2), но наводит на полезные размышления. Вышеизложенная итерационная формула (25) впервые была построена для изучения динамики популяций особей определённого вида в зависимости от истребления ареала пищи Ферхюльстом и носит его имя.
Мы видим, что одна и та же математическая модель может содержать в себе различные аспекты приложений, что вполне характерно для духа прикладной математики.
3. Методы решения алгебраических уравнений
Большинство задач физики, экономики, социологии, биологии и других областей знания приводят к решению алгебраических уравнений или систем уравнений.
Несмотря на наличие множества приближённых методов, в настоящее время, пожалуй, нет общего подхода для решения любого нелинейного уравнения и тем более нелинейной системы уравнений. Поэтому, в каждом частном случае приходится исследовать уравнения и строить соответствующие алгоритмы, комбинируя идеи разных численных методов. Так, что решение нелинейного уравнения, в настоящее время, скорее искусство, чем наука. Хотя, известные программные продукты современных фирм позволяют, во многих случаях, упростить поиск корней.
Перейдём на изложение основных известных и наиболее популярных методов. Прежде отметим, что при отыскании приближённых значений корней приходится решать две задачи:
а) отделение корней, т.е. отыскание достаточно малых областей в каждой из которых находится корень;
б) вычисление корней с заданной точностью.
3.1 Метод деления отрезка пополам (метод дихотомии)
Перед началом решения уравнения
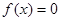 (36) (36)
мы должны выделить интервал поиска решения 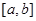 , т.е. ответить на вопрос а) предыдущего параграфа. Для этого используется теорема Вейерштрасса. , т.е. ответить на вопрос а) предыдущего параграфа. Для этого используется теорема Вейерштрасса.
Теорема Вейерштрасса: Если на концах некоторого отрезка непрерывная функция 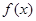 принимает значения разных знаков, то на этом отрезке уравнение (36) имеет хотя бы один корень. принимает значения разных знаков, то на этом отрезке уравнение (36) имеет хотя бы один корень.
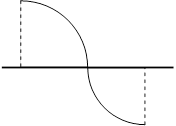
Эта теорема выражает геометрически очевидный факт (рис.4), состоящий в том, что если в точках 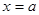 и и  график непрерывной функции находится в график непрерывной функции находится в
разных полуплоскостях от оси 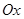 , то найдётся точка , то найдётся точка 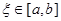 , такая что график этой функции пересекается с осью , такая что график этой функции пересекается с осью 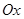 в точке в точке 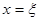 , т.е. , т.е. 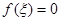 . .
а 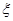 bЗамечание: если при этом bЗамечание: если при этом 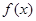 имеет первую имеет первую
производную 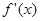 - не меняющую знака, то корень единственный. - не меняющую знака, то корень единственный.
Таким образом, мы можем сказать, что уже умеем
Рис. находить отрезок 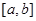 , где находится корень , где находится корень
уравнения (36), но этот отрезок можно уменьшать, основываясь на теореме Вейерштрасса.
Для этого в качестве первого приближения к корню берём середину отрезка 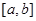 , т.е. , т.е.
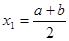 (38) (38)
Этой точкой отрезок 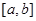 делится на два равных отрезка: делится на два равных отрезка: 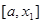 и и 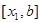 . Используя теорему Вейерштрасса, устанавливаем в каком из этих отрезков лежит корень, т.е. на концах какого из этих двух отрезков функция . Используя теорему Вейерштрасса, устанавливаем в каком из этих отрезков лежит корень, т.е. на концах какого из этих двух отрезков функция 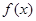 принимает разные знаки. С этим отрезком действуем также, т.е. выбираем в качестве второго приближения к корню середину этого отрезка принимает разные знаки. С этим отрезком действуем также, т.е. выбираем в качестве второго приближения к корню середину этого отрезка 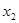 и продолжаем этот итерационный процесс, пока отрезок поиска решения и продолжаем этот итерационный процесс, пока отрезок поиска решения 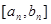 не станет меньше требуемой точности не станет меньше требуемой точности 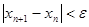 . .
Оценка погрешности вычислений по методу деления отрезка пополам производится по очевидной формуле:
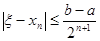 (39) (39)
Ясно, что 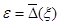 , а относительная погрешность , а относительная погрешность 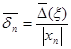 . .
Изложенный метод легко программируется и даёт сходимость с точностью (39), хотя при практических вычислениях чаще пользуются комбинациями различных численных методов, добиваясь более быстрой сходимости процесса.
3.2 Метод ложного положения (метод хорд).
В основе метода лежит линейная интерполяция по двум значениям функции, имеющим противоположные знаки. Этот метод зачастую даёт более быструю сходимость, чем метод деления отрезка пополам.
Для иллюстрации алгоритма метода ложного положения (метода хорд), рассмотрим рис.5.
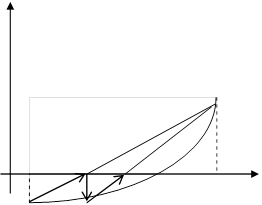
рис.5.
Сначала находим отрезок 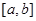 где где
yзаведомо известно, что существует
корень 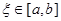 , т.е. , т.е. 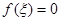 , для этого по теореме Вейерштрасса должно быть , для этого по теореме Вейерштрасса должно быть  . .
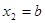
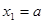 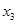 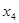 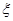
В качестве первого приближения к корню берём 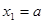 , второе приближение , второе приближение 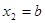 . Для нахождения следующего приближения соединяем эти две точки отрезком прямой. Точку пересечения этого отрезка берём в качестве третьего приближения . Для нахождения следующего приближения соединяем эти две точки отрезком прямой. Точку пересечения этого отрезка берём в качестве третьего приближения 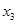 , далее значение функции , далее значение функции 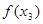 сравнивается с сравнивается с 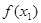 и и 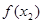 , где будут разные знаки, в дальнейшем используется именно тот отрезок вместо , где будут разные знаки, в дальнейшем используется именно тот отрезок вместо 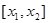 , и т.д. Соответствующая итерационная формула имеет вид: , и т.д. Соответствующая итерационная формула имеет вид:
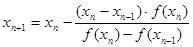 (40) (40)
где 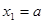 и и 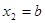 . .
Ясно, что эта итерационная формула требует, чтобы 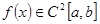 , а также , а также 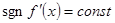 и и 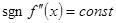 . .
Точность вычисления корня методом хорд оценивается неравенством
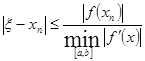 (41) (41)
предельная относительная погрешность:
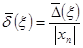 (42) (42)
где 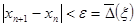 . .
3.3 Метод Ньютона (метод касательных)
Хотя метод ложного положения даёт более быструю сходимость, чем метод деления отрезка пополам, проверка условий применимости метода хорд достаточно громоздка, поэтому рассмотрим метод Ньютона, который иногда называют методом касательных.
В отличие от предыдущих методов здесь не требуется предварительно искать отрезок 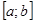 , где , где 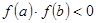 . Для решения уравнения . Для решения уравнения
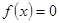 (43) (43)
в методе Ньютона задаёмся требуемой точностью 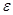 (абсолютная погрешность). Далее произвольно выбираем начальное приближение (абсолютная погрешность). Далее произвольно выбираем начальное приближение 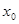 . Считаем, что . Считаем, что
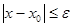 (44) (44)
для нахождения следующего приближения 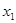 , где , где
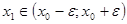 (45) (45)
воспользуемся формулой Тейлора для 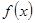 : :
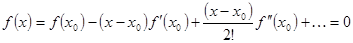 (46) (46)
Отбрасывая члены разложения, содержащие производные выше первого порядка, получаем уравнение для определения приближённого значения корня 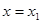 : :
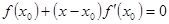 (47) (47)
т.е.
 (48) (48)
Зная 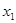 , новое, улучшенное значение , новое, улучшенное значение 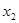 находим аналогично находим аналогично
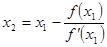 (49) (49)
и вообще
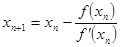 (50) (50)
Вычисления надо продолжать до тех пор, пока не достигнем требуемой абсолютной погрешности 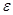 : :
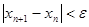 (51) (51)
Предельная относительная погрешность равна:
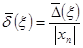 (52) (52)
Скорость сходимости итерационной формулы Ньютона (50) оценивается неравенством:
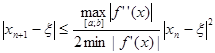 (53) (53)
Ясно, что скорость сходимости выше, чем в методе хорд. Однако, здесь так же нужно иметь в виду, что 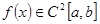 , а также , а также 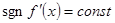 и и 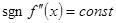 , а эти условия трудно проверить, что и является отталкивающим фактором для исследователей. Кроме того, для применения метода Ньютона, нужно достаточно точное знание начального приближения , а эти условия трудно проверить, что и является отталкивающим фактором для исследователей. Кроме того, для применения метода Ньютона, нужно достаточно точное знание начального приближения 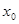 . .
Здесь, так же как и в методе хорд, легко представить этот процесс геометрически. Взяв начальное приближение 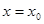 , в этой точке проводится касательная к графику функции , в этой точке проводится касательная к графику функции 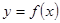 . Пересечение касательной с осью абсцисс . Пересечение касательной с осью абсцисс 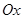 принимается за первое приближение. Далее касательная проводится в точке принимается за первое приближение. Далее касательная проводится в точке 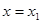 , пересечение касательной с осью , пересечение касательной с осью 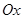 берётся в качестве второго приближения и т.д. берётся в качестве второго приближения и т.д.
Литература
1. Высшая математика - Сапунов И.С. - М. 2000 г.
|