Реферат «
Введение в численные методы
»
Тема: «Методы предварительных эквивалентных преобразований и итерационные методы с минимизацией невязки для решения СЛАУ»
1.
Методы предварительных эквивалентных преобразований
1.1
Преобразование вращения
Следующий важный подход к решению алгебраических систем уравнений базируется на применении эквивалентных преобразований с помощью унитарных матриц, сводящем исходную матрицу к эквивалентной ей диагональной.
Смысл этого подхода состоит в том, чтобы последовательно, умножением слева и / или справа на специальные унитарные матрицы, превратить некоторые компоненты исходной матрицы в нуль.
Матрица S
называется унитарной, если ее произведение со своей комплексно сопряженной равно единичной матрице. Это означает, что комплексно сопряженная матрица равна обратной матрице:
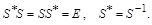
Известной унитарной матрицей является матрица вращения
,которая применяется для поворота на заданный угол вектора, принадлежащего некоторой плоскости, вокруг начала координат. В двумерном случае вектор 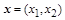 поворачивается на угол поворачивается на угол 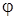 путем умножения на матрицу путем умножения на матрицу
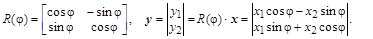
Чтобы сохранить эквивалентность результирующей матрицы при умножении ее на матрицу вращения, необходимо исходную матрицу умножать справа на 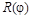 и слева на и слева на 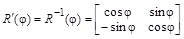 . Умножение же матрицы вращения на вектор дает такой же по величине вектор, но повернутый на заданный угол. . Умножение же матрицы вращения на вектор дает такой же по величине вектор, но повернутый на заданный угол.
Поворот вектора в многомерном пространстве на произвольный угол можно представить, как последовательность плоских вращений каждой проекции на некоторый угол. Если подобрать угол вращения так, чтобы в плоском повороте одну из проекций вектора совместить с координатной осью, то вторая проекция в этой плоскости становится равной нулю.
Частные повороты вектора в многомерном пространстве с помощью матрицы вращения можно выполнять, если ее расширить до матрицы размера  следующим образом: следующим образом:
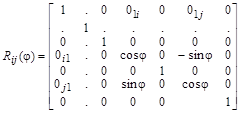 . .
Индексы i, j
обозначают матрицу вращения, поворачивающую вектор в плоскости 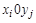 на угол на угол 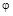 . .
Теперь частное эквивалентное преобразование матрицы A
вращением на угол 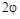 записываются так: записываются так:
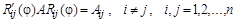 . .
Условие превращения в нуль ij-
тых элементов симметричной матрицы A
можно получить методом неопределенных коэффициентов на двумерной матрице:
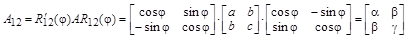 . .
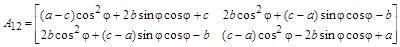 . .
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Угол поворота, при котором 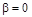 , находится из уравнения , находится из уравнения
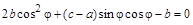 . .
Разделив на 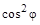 и обозначив и обозначив 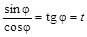 , , 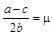 , получим квадратное уравнение для тангенса требуемого угла поворота , получим квадратное уравнение для тангенса требуемого угла поворота
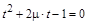 . .
Из двух решений для тангенса выбирается такое, чтобы 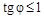 . В этом случае . В этом случае 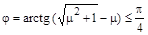 . Подставив выражение для угла в соотношения для диагональных элементов, после тригонометрических преобразований получаются следующие формулы: . Подставив выражение для угла в соотношения для диагональных элементов, после тригонометрических преобразований получаются следующие формулы:
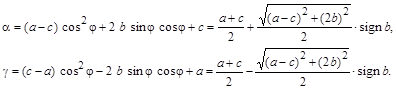
Для получения результирующей матрицы выполнять матричное умножение трех матриц совсем необязательно. Структура матриц вращения вызывает при умножениях изменение только тех элементов исходной матрицы, которые находятся на i-
той и j-
той строчках и на i-
том и j-
том столбцах. Изменения представляются суммами элементов, стоящих в строчках и столбцах, умноженных на синус или косинус угла  в соответствии с формулами, где j>i
: в соответствии с формулами, где j>i
:
преобразования строк – 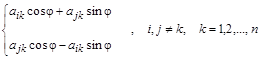 ; ;
преобразование столбцов –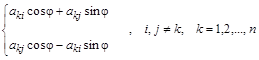 . .
На пересечениях i
-й строки и i-
того столбца и j
-й строки и j-
того столбца располагаются соответственно вычисленные выше 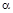 и и 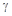 , а на местах ij
-того и ji
-того элементов вставляются нули. , а на местах ij
-того и ji
-того элементов вставляются нули.
Для приведения к диагональной матрице необходимо выполнить 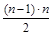 таких элементарных преобразований. таких элементарных преобразований.
1.2
Ортогональные преобразования отражением
Следующей важной унитарной матрицей, с помощью которой в различных алгоритмах выполняются ортогональные преобразования, являются матрицы отражения. Использование этого инструмента позволяет, например, последовательными эквивалентными преобразова-ниями свести исходную матрицу к верхней треугольной (QR-алгоритмы), трех или двух диагональным и т.д.
Смысл этого подхода состоит в том, чтобы умножением матрицы A
слева на специально подобранную унитарную матрицу 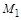 один из столбцов исходной матрицы (например, один из столбцов исходной матрицы (например, 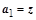 ) преобразовать в вектор, параллельный единичному координатному вектору ) преобразовать в вектор, параллельный единичному координатному вектору 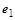 ( (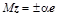 или или 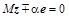 ). Тогда, последовательно подбирая нужные унитарные матрицы ). Тогда, последовательно подбирая нужные унитарные матрицы 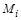 и соответствующие единичные векторы и соответствующие единичные векторы 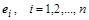 , после n
циклов эквивалентных преобразований можно будет получить верхнюю треугольную матрицу: , после n
циклов эквивалентных преобразований можно будет получить верхнюю треугольную матрицу:
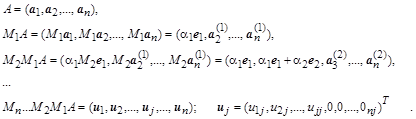
При выборе в качестве начального вектора 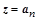 и умножениях матрицы A
на ортогональные матрицы справа в конечном счете можно получить нижнюю треугольную матрицу. и умножениях матрицы A
на ортогональные матрицы справа в конечном счете можно получить нижнюю треугольную матрицу.
Весь вопрос состоит в том, как формировать унитарную матрицу с заданными свойствами из векторов 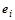 и столбцов и столбцов 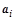 матрицы A
. матрицы A
.
Из аналитической геометрии известно, что любые векторы, лежащие в плоскости, взаимно перпендикулярны с ее нормалью, т.е. их проекции на нормаль равны нулю. Последнее эквивалентно равенству нулю скалярных произведений.
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Чтобы (k+
1) – мерный векторный треугольник 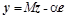 сделать параллельным k-
мерной гиперплоскости с нормалью n
(вектор единичной длины, перпендикулярный плоскости), необходимо приравнять нулю скалярное произведение: (n
, y
)=0. сделать параллельным k-
мерной гиперплоскости с нормалью n
(вектор единичной длины, перпендикулярный плоскости), необходимо приравнять нулю скалярное произведение: (n
, y
)=0.
Пусть вектор z
не параллелен плоскости, заданной своей нормалью, тогда его проекции на эту плоскость и нормаль соответственно будут представлены векторами 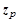 и и 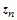 . Вектор z
и вектор зеркально-симметричный ему . Вектор z
и вектор зеркально-симметричный ему 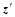 через эти проекции можно выразить так: через эти проекции можно выразить так:
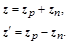
Разрешив первое относительно 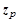 и подставив его в и подставив его в 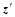 , получим , получим
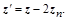
Проекцию вектора 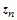 можно заменить скалярным произведением (n
, z
) и подставить в выражение для можно заменить скалярным произведением (n
, z
) и подставить в выражение для 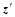 , выразив тем самым зеркально отраженный вектор через исходный вектор и нормаль гиперплоскости: , выразив тем самым зеркально отраженный вектор через исходный вектор и нормаль гиперплоскости:
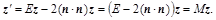
Здесь M
представляет унитарную матрицу, преобразующую произвольный вектор в зеркально отраженный. В том, что матрица унитарная, нетрудно убедиться, проверив ее произведение со своей комплексно сопряженной:
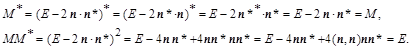
Выражение для зеркально отраженного вектора позволяет представить нормальный вектор в виде линейной функции от задаваемого вектора z
:
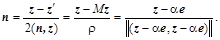
Число 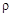 в знаменателе является нормирующим множителем. Нормальный вектор представляющий гиперплоскость обязан иметь единичную длину. Коэффициент в знаменателе является нормирующим множителем. Нормальный вектор представляющий гиперплоскость обязан иметь единичную длину. Коэффициент 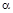 , который в общем случае является комплексным числом, необходимо выбрать так, чтобы скалярное произведение , который в общем случае является комплексным числом, необходимо выбрать так, чтобы скалярное произведение 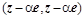 было больше нуля. Если учесть соотношение для согласованных норм: было больше нуля. Если учесть соотношение для согласованных норм: 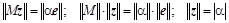 , то , то
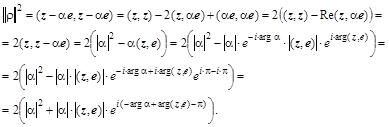
Выбрав 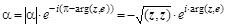 для комплексных матриц или для комплексных матриц или 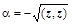 – для действительных матриц, будем иметь – для действительных матриц, будем иметь
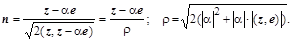
Такое нормирование не нарушает коллинеарности отраженного и единичного векторов:
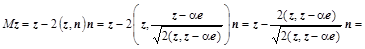
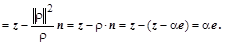
Рассмотрим пример воздействия ортогонального преобразования на матрицу
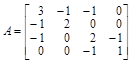 . .
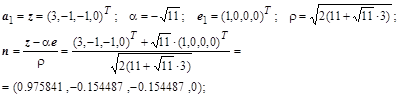
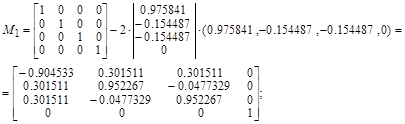
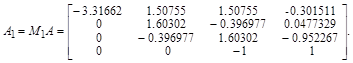
Приведенная методика получения унитарных (и ортогональных в частности) матриц используется во многих стандартных алгоритмах в качестве инструмента частичного преобразования исходных матриц к двух или трех диагональным, для которых в дальнейшем применяются рекуррентные формулы получения решения уравнений, называемые в литературе методом прогонки
для систем с ленточными матрицами.
2.
Итерационные методы с минимизацией невязки
2.
1
Ускорение сходимости итерационных методов
Точные методы получения решений, использующие рассмотренные эквивалентные преобразования полностью заполненной матрицы, требуют выполнения числа операций, пропорционального кубу размерности системы, и свободной памяти для хранения исходных и промежуточных значений – пропорциональной квадрату размера матрицы. Поэтому для сверх больших систем (число неизвестных больше нескольких сотен) ориентируются в основном на применение приближенных, итерационных методов.
Привлекательность тех или иных итерационных методов определяется скоростью сходимости итерационного процесса. Теоретически доказано, что итерационный процесс Гаусса-Зейделя сходится к решению при любом начальном значении искомого значения вектора решений, однако количество итерационных циклов может во много раз превышать число неизвестных (размерность матрицы). Это вызвало к жизни множество модификаций алгоритмов, обладающих большей скоростью сходимости.
Процедуры ускорения связаны с построением очередного вектора по одному или нескольким его значениям на предыдущих итерационных циклах. Фактически речь идет о построении на каждом шаге итераций интерполирующей функции с векторным аргументом, по которой вычисляют очередной вектор для подстановки. Для вычисления вектора 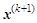 на (k+
1) – ом шаге итераций необходимо сначала получить величину на (k+
1) – ом шаге итераций необходимо сначала получить величину 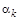 и единичный вектор направления и единичный вектор направления  и просуммировать предыдущий вектор и просуммировать предыдущий вектор 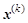 с добавочным вектором: с добавочным вектором:
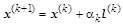 . .
Подстановка последнего в уравнение (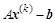 ) образует вектор ) образует вектор 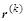 из покомпонентных невязок. Для задания структурной взаимосвязи каждой невязки с соответствующей компонентой вектора из покомпонентных невязок. Для задания структурной взаимосвязи каждой невязки с соответствующей компонентой вектора 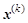 и образования функционала (скалярной функции от вектора невязок) возмем скалярное произведение вектора невязки на вектор-строку и образования функционала (скалярной функции от вектора невязок) возмем скалярное произведение вектора невязки на вектор-строку 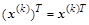 : :
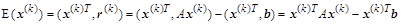 . .
После подстановки очередного вектора функционал получит новое значение, которое будет зависеть от некоторого скаляра 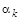 : :
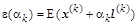 . .
Чтобы невязки на каждом шаге итераций становились меньше, желательно соответствующим образом выбирать 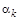 . Найдем такое значение . Найдем такое значение 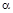 , при котором , при котором 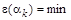 . Для этого приравняем производную по . Для этого приравняем производную по 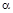 нулю. Индекс номера итерации пока опустим. нулю. Индекс номера итерации пока опустим.
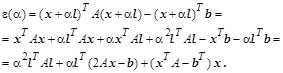
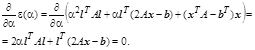
Из последнего равенства для (k+
1) – й итерации величина шага 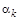 в направлении вектора в направлении вектора  должна быть вычислена так:
должна быть вычислена так:
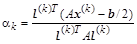 . .
Если единичные векторы направления последовательно выбирать равными координатным, т.е. 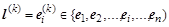 , то будет реализован метод Гаусса-Зейделя (метод покоординатного спуска в задачах оптимизации). , то будет реализован метод Гаусса-Зейделя (метод покоординатного спуска в задачах оптимизации).
Выбирая направление изменения очередного вектора в сторону локального убывания, т.е. в сторону, противоположную вектору градиента функционала, получается метод быстрого спуска. В этом случае
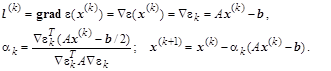
2.2
Метод сопряженных направлений
Среди методов, связанных с выбором направления существуют методы, в которых к векторам направлений предъявляются требования их взаимной сопряженности 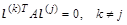 , т.е. матрица A
преобразует вектор , т.е. матрица A
преобразует вектор 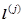 в вектор, ортогональный вектору в вектор, ортогональный вектору  . Доказано, что выбор направлений из множества сопряженных позволяет при любом начальном . Доказано, что выбор направлений из множества сопряженных позволяет при любом начальном 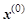 свести задачу к точному решению не более, чем за n
шагов, если матрица симметричная и положительно определенная ( свести задачу к точному решению не более, чем за n
шагов, если матрица симметричная и положительно определенная (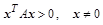 ) размера ) размера  . .
Классическим набором сопряженных векторов являются собственные векторы матрицы (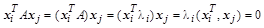 ). Однако задача их определения сложнее решения заданной системы уравнений. Не менее сложна и задача построения произвольной системы ортогональных векторов. ). Однако задача их определения сложнее решения заданной системы уравнений. Не менее сложна и задача построения произвольной системы ортогональных векторов.
В то же время примером ортогональных направлений являются направления вектора градиента и нормали в заданной точке некоторой гиперповерхности. Такая поверхность выше была представлена функционалом в виде скалярного произведения вектора невязки и вектора x
, которая и определяла направление спуска по направлению градиента. Если, используя такой же подход к вычислению 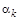 , в выражении для последнего вектор невязок дополнительно модифицировать, как показано ниже, то рекуррентно вычисляемые очередные направления окажутся сопряженными: , в выражении для последнего вектор невязок дополнительно модифицировать, как показано ниже, то рекуррентно вычисляемые очередные направления окажутся сопряженными:
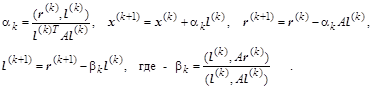
Выбрав в начале итераций 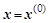 и и 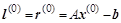 , после выполнения приведенных вычислений в (n-
1) цикле будут получены векторы направлений, удовлетворяющие соотношениям , после выполнения приведенных вычислений в (n-
1) цикле будут получены векторы направлений, удовлетворяющие соотношениям
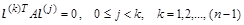 , ,
а векторы невязок будут ортогональными:
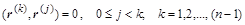 . .
Относительно метода сопряженных градиентов доказывается, что, если матрица (положительно определенная и симметричная) имеет только m
(m<n
) различных собственных значений, то итерационный процесс сходится не более, чем за m
итераций. Однако в практической реализации скорость сходимости существенно зависит от величины меры обусловленности 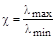 и в итерационном процессе может быть оценена согласно неравенству:
и в итерационном процессе может быть оценена согласно неравенству:
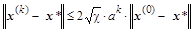 , ,
где 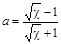 – коэффициент, степень которого на каждом шаге итерационного процесса показывает во сколько раз уменьшилось расстояние до вектора точного решения x
*. – коэффициент, степень которого на каждом шаге итерационного процесса показывает во сколько раз уменьшилось расстояние до вектора точного решения x
*.
Чем больше 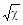 , тем ближе a
к единице и, следовательно, степени a
уменьшаются медленнее. В литературе описываются модифицированные методы сопряженных градиентов, которые тем или иным способом включают в итерационный процесс подобные (конгруэнтные
– для комплексных матриц) преобразования, предварительно уменьшающие меру обусловленности. , тем ближе a
к единице и, следовательно, степени a
уменьшаются медленнее. В литературе описываются модифицированные методы сопряженных градиентов, которые тем или иным способом включают в итерационный процесс подобные (конгруэнтные
– для комплексных матриц) преобразования, предварительно уменьшающие меру обусловленности.
Литература
1. Бахвалов И.В. Численные методы. БИНОМ, 2008. – 636c.
2. Волков Е.А. Численные методы. Изд-во ЛАНЬ, 2004. – 256.
3. Демидович Б.П., ред., Марон И.А., Шувалова Э.З. Численные методы анализа. Издательство ЛАНЬ, 2008.
4. Пантелеев А.В., Киреев В.И., Пантелеев В.И., Киреев А.В. Численные методы в примерах и задачах. М: Высшая школа, 2004. – 480c.
5. Пирумов У.Г., Пирумов О.Г. Численные методы. Изд-во: ДРОФА, 2004. – 224c.
|