Министерство образования российской федерации
Московская государственная академия тонкой химической технологии
им. М.В. Ломоносова
Кафедра химии и технологии основного органического синтеза
АТТЕСТАЦИОННАЯ РАБОТА
Сравнительный анализ рециркуляционных схем
на примере реакции изомеризации
На соискание степени бакалавра по направлению 550800
"Химическая технология и биотехнология"
Зам. Зав. Кафедрой ХТООС. Проф. Тимошенко А.В.
Руководитель работы. Доц. Назанский С.Л.
Соискатель Ворошилова Н.В.
МОСКВА 2004 г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ.. 3
Глава 1. Литературный обзор. 6
1.1. Рециркуляционные процессы. 7
1.2. Методы оценки энергетических затрат в реакционно-ректификационных процессах. 12
1.3. Постановка задачи. 13
Глава 2. Расчетно-аналитическая часть. 14
2.1. Анализ стационарных состояний рециркуляционного реакционно-ректификационного процесса. 14
2.1. Рециркуляционная схема с рециклом, охватывающим два реактора. 15
2.2. Рециркуляционная схема с рециклом, охватывающим один реактор. 19
Глава 3. Расчетная часть. 25
ВЫВОДЫ... 34
Список литературы... 35
Конечной целью функционирования любой химико-технологической схемы (ХТС) является достижение полной конверсии реагентов и разделение продуктов реакции на отдельные компоненты с заданной степенью чистоты. Однако, при использовании линейных ХТС в большинстве случаев эти цели недостижимы из-за наличия кинетических и термодинамических ограничений, накладываемых спецификой структур диаграмм фазового и химического равновесий. В частности, для обратимых реакций в реакторе любого типа невозможно достижение полной конверсии реагентов [5], а ее максимально возможное значение определяется состоянием химического равновесия. С другой стороны, наличие азеотропов в реакционной смеси часто не позволяет выделить продукты реакции требуемого качества [2]. Часто, при осуществлении медленно протекающих реакций из-за непомерного увеличения объема реактора невозможно достичь равновесия, эти реакции осуществляются с намного меньшим выходом продуктов, чем могло бы быть в условиях равновесия. Однако, если проводить процесс с небольшими превращениями за однократный пропуск при одновременном выводе из системы продуктов реакции и с последующим возвращением в систему непрореагировавших веществ, то можно достичь 100-процентного превращения исходного сырья.
Реклама

Кроме того, как правило, многие химические реакции сопровождаются параллельно или последовательно протекающими побочными превращениями. Скорость этих реакций и соотношение выходов продуктов в реакциях изменяются в зависимости от условий процесса. Максимальному выходу желаемого продукта будет соответствовать определенная глубина превращения исходного сырья, после которой начнут преобладать побочные реакции.
Таким образом, преодоление указанных ограничений возможно при организации селективного обмена веществом реакционной зоны с окружающей средой [20]. Наличие селективного обмена, независимо от способа его реализации, позволяет, с одной стороны, создавать в реакционной зоне необходимые условия для протекания целевых реакций с высокими скоростями, а с другой стороны, обеспечивать в системе в целом высокую конверсию (вплоть до полного исчерпывания реагентов) и селективность [1]. Все это, в конечном счете, и является основой создания современных энергосберегающих и экологически безопасных технологий [1].
Одним из способов организации такого селективного обмена является рециркуляция [8], которая может быть как внешней, так и внутренней.
Внешняя рециркуляция применяется в настоящее время практически во всех химико-технологических процессах [1], когда процессы синтеза и разделения проводятся последовательно и раздельно. Примером организации внутренней рециркуляции являются совмещенные реакционно-массообменные процессы [4], в которых химические реакции и процессы разделения проводятся одновременно и в рамках одного аппарата.
Очевидно, что разработка качественных и количественных методов анализа и синтеза технологических схем, использующих принцип селективного обмена веществом с окружающей средой, в частности рециркуляционных и совмещенных процессов, открывает возможности построения ХТС, обеспечивающих практически полную конверсию реагентов при минимальных энергетических затратах.
В химико-технологических системах, где в реакторах используются дорогие катализаторы, для увеличения их срока службы используют схемы, в которых до основного реактора ставят еще один реактор с более дешевым катализатором, в котором происходит очищение сырья от примесей, вредных для дорогого катализатора, и неполное превращение исходного сырья. А также для снятия теплоты реакции в первом реакторе, так как из-за больших скоростей возникает большой тепловой эффект реакции.
Реклама

В таких схемах существуют различные варианты охвата реакторов рециклом: можно подавать рецикл либо на вход первого реактора, либо на вход второго.
Таким образом, в данной работе рассматриваются две схемы с различной подачей рецикла с позиции минимальных энергетических затрат, необходимых для достижения заданной конверсии и селективности.
Основной стратегией защиты окружающей среды от негативного воздействия химической промышленности является создание экологически безопасных технологий, позволяющих наиболее полно использовать сырье и энергию [1].
Однако существует ряд ограничений химического и термодинамического характера, препятствующих реализации этой стратегии. Наличие химических ограничений связано, прежде всего, с тем, что практически все химические реакции являются обратимыми, и, следовательно, максимально возможное значение конверсии в простой проточной системе ограничено химическим равновесием. Кроме того, существуют и кинетические ограничения, из-за которых конверсия за один проход оказывается весьма низкой. Ограничения термодинамического характера проявляются на стадии разделения продуктов реакции и определяются структурой диаграммы фазового равновесия.
Одним из подходов к преодолению указанных ограничений является организация селективного обмена реакционной зоны веществом с окружающей средой, а также использование специальных методов разделения, базирующихся, например, на принципе перераспределения полей концентраций.
Существует несколько способов реализации селективного обмена веществом.1) Возврат непрореагировавших веществ со стадии разделения на стадию химического превращения (рециркуляция). Такой способ организации уже давно используется в промышленности. Использование рециркуляции позволяет проводить процесс при высоких концентрациях исходных реагентов, а, следовательно, и при высоких скоростях реакций [6-9]. Кроме того, варьируя состав рецикла, можно уменьшать образование побочных продуктов.2) Мембранные процессы, в которых высокая концентрация реагентов в зоне реакции создается за счет того, что мембрана выпускает преимущественно только продукты реакции.3) Использование принципа совмещения, когда химическое превращение и разделение объединены в рамках одного аппарата. Такие процессы начали использоваться сравнительно недавно и получили название совмещенные реакционно-массобменные процессы [4, 36]. Совмещенные процессы обладают рядом преимуществ, в частности, это отсутствие внешних рециркулирующих потоков и возможность более компактной организации процесса по сравнению с традиционной системой с рециклом.
В настоящее время рециркуляция находит широкое применение во многих промышленных крупнотоннажных процессах, таких как каталитический крекинг, пиролиз, получение полиэтилена высокого давления и многих других.
Любая типовая ХТС с рециклом состоит из узла смешения, реакторного узла и узла разделения (рис.1.1).
Состав рециркулирующего потока может быть самым различным: он может представлять собой как смесь всех компонентов реакции, так и смесь, содержащую один или несколько компонентов.
Реагенты и продукты
Реагенты Продукты
Рис.1.1. Рециркуляционная система.
Однако в любом случае, питание реактора складывается из свежего сырья и рециркулята, и должно иметь тогда большее количество, по крайней мере, одного из реагентов, чем при загрузке реактора лишь свежим сырьем. Вследствие этого, степень превращения за один проход через реакционный объем будет ниже степени превращения, рассчитанной для случая отсутствия рецикла.
Однако производительность реактора и общая степень превращения в системе по целевому продукту увеличится.
Таким образом, наличие рециклов позволяет, с одной стороны, достигать высоких скоростей химического превращения в реакторе (за счет возврата не прореагировавших реагентов в реакционную зону и уменьшения времени контакта в ней), а, с другой стороны, реализовывать селективный вывод целевых продуктов из системы, что в конечном итоге позволяет получать в схеме любую заданную конверсию. Таким образом, рециркуляционные процессы позволяют снимать термодинамические ограничения, связанные с химическим равновесием, и кинетические ограничения, связанные с низкими скоростями реакций. Следовательно, можно утверждать, что теоретически для любой обратимой реакции (независимо от скорости ее протекания и величины константы равновесия) в технологической схеме, состоящей из реактора и узла разделения охваченных рециклом, всегда может быть достигнуто полное превращение реагентов при условии, что узел разделения позволяет выделять в чистом виде продукты реакции и формировать поток рецикла требуемого состава.
Теоретические основы рециркуляции разрабатывались с 30-х годов, когда в работах [11.12] было показано, что при введении рециркуляции увеличивается выход целевых продуктов и производительность процесса. Для максимальной производительности единицы объема реактора процесс следует проводить при температуре и давлении, соответствующих максимальной скорости реакции. Каталитические реакции должны проводиться в присутствии катализаторов, проявляющих высокую активность при малых степенях превращения. Катализатор следует выбирать путем сравнения его работы не при одинаковых условиях, а исходя из способности обеспечения высокой скорости в специфических для рассматриваемого катализатора условиях – путем выявления потенциальных возможностей катализаторов.
В работе М.Ф. Нагиева [9] был сформулирован принцип супероптимальности, сущность которого состоит в том, что реакционный процесс следует проводить при низких конверсиях и с наибольшим количеством рециркулята, а также следует формировать состав рецикла таким образом, чтобы концентрации реагентов в реакторе соответствовали максимальной скорости основной реакции. Развитие теории рециркуляции получило продолжение в работах СИ. Дуева [13-18], который показал возможность достижения полного исчерпывания исходных и промежуточных реагентов в системе реактор-блок разделения. Дальнейшие исследования рециркуляционных процессов с применением системного подхода были продолжены В.В. Кафаровым [19-21]. А.В. Солохиным [22, 23] и другими исследователями.
Одним из методов исследования рециркуляционных процессов являются численные методы. Для рециркуляционной системы записывается математическая модель, которая может состоять из алгебраических или дифференциальных уравнений. Уравнения, входящие в математическую модель, как правило, нелинейны, особенно для систем с обратными связями (рециклами). Следовательно, система уравнений может иметь несколько решений, среди которых могут быть решения, не имеющие физического смысла. В зависимости от выбранного начального приближения расчет, проводимый с помощью численных методов, может сходится к тому или иному решению. Подчас бывает очень трудно выбрать хорошее начальное приближение, поскольку искомое решение лежит в узком диапазоне значений параметров. Наиболее распространенным методом решения систем нелинейных алгебраических уравнений является метод Ньютона-Рафсона [24.98], который обеспечивает достаточно хорошую скорость сходимости. Однако, когда исследуемый процесс характеризуется множественными стационарными состояниями (математическая модель имеет несколько физически осмысленных решений), возникает вероятность пропустить какое-нибудь стационарное состояние. Для снижения вероятности потери решения в последнее время стал применяться метод гомотопического продолжения [27], в котором исходная система уравнений преобразуется путем ввода дополнительного параметра (параметра гомотопии) и искомые решения приобретают вид ветвей в пространстве переменных процесса и параметра гомотопии. Например, в работе [92] проводится численное исследование совмещенного реакционно-ректификационного процесса получения этиленгликоля, в котором в качестве параметра гомотопии выступала величина объема реакционной зоны, и в зависимости от параметра гомотопии исходная модель могла плавно переходить от модели простой ректификации к модели совмещенного процесса.
Для решения задачи численным методом можно использовать такие программы как ChemCad, PRO-2, AspenPlus, HighSym и т.д. Программный пакет ChemCad базируется на сложных содержательных математических моделях, которые достаточно полно отражают реальные процессы, протекающие в аппаратах. Эта программа, как и множество других, с успехом используется для решения многочисленных задач, связанных с анализом и синтезом ХТС, основными элементами которых являются реакционные и массообменные аппараты. Однако, как правило, существующие программные средства позволяют осуществлять численное моделирование ХТС лишь в поверочном варианте. При такой постановке задачи в качестве заданных рассматриваются параметры состояния входных потоков (расходы, составы и теплосодержания потоков), конструкционные параметры аппаратов (например, длина/объем реакторов, общая высота и местоположение питаний и отборов ректификационных колонн и т.д.), а также значения управляющих режимных параметров (флегмовые или паровые числа, соотношения или абсолютные значения расходов выходных потоков, коэффициенты рециркуляции или величины потоков рецикла) рассматриваемого химико-технологического процесса. В результате проведения расчетов определяются значения параметров выходных потоков, а также распределенные и нераспределенные внутренние переменные ХТС, такие, например, как профили изменения температуры и составов фаз по высоте колонны, температуры и давления в аппарате и т.д.
В случае проектной постановки задачи расчета ХТС заданными считаются параметры состояния входных и выходных потоков. Кроме этих параметров в качестве задаваемых свободных параметров рассматривается ряд конструкционных или режимных параметров процесса, причем число таких переменных определяется числом степеней свободы рассматриваемой ХТС. Остальные конструкционные и режимные параметры, также как и внутренние переменные, рассматриваются как решения задачи. В общем случае, выбор конкретного набора свободных параметров произволен и определяется спецификой рассматриваемой задачи.
Вторая группа методов исследования рециркуляционных систем - это упрошенные качественные методы [23, 77]. Для упрощения анализа вводят различные допущения при описании реакционной и разделительной составляющих процесса. При описании реакционного блока могут использоваться упрошенные механизмы реакции или допущение о бесконечном объеме реактора, которое позволяет считать, что состав на выходе из него всегда химически равновесный [34] и т.д. При анализе разделительных процессов также можно вводить предельные допущения. В частности, можно исследовать процесс ректификации при бесконечной высоте колонны и режиме полного орошения. Тогда, в соответствии с положениями термодинамико-топологического анализа [2] для определения возможных составов продуктовых потоков разделения можно использовать фазовый портрет равновесного открытого испарения реакционной смеси. При таком "запределивании" параметров разделения исследование рециркуляционной системы можно свести к решению системы уравнений материальных балансов реактора, узла смешения и колонны, в которой реализуются четкие и получеткие разделения. Такой способ упрощения довольно широко используется различными авторами [32, 41, 49] и дает хорошие результаты. Однако остается открытым вопрос о сохранении полученных результатов анализа при переходе к реальным процессам.
Еще один метод упрощения анализа рециркуляционных систем состоит в линеаризации [68.69] структурных элементов диаграмм фазового и химического равновесия, т.е. аппроксимации разделяющих многообразий парожидкостного равновесия, бинодальных многообразий и многообразий химического равновесия. Например, в работе [68] линия химического равновесия представляется в виде ломаной, каждый участок которой описывается своим уравнением прямой. Поскольку при допущениях о бесконечной высоте колонны и полном орошении для ректификационной колонны и равновесном реакторе записываются только линейные уравнения материальных балансов (тепло не учитывается), то математическая модель превращается в систему линейных уравнений, которую можно решить любым из известных методов.
Системы нелинейных дифференциальных уравнений (динамические системы) также можно линеаризовать путем разложения их в ряд Тейлора в окрестностях особых точек [28.29.37]. По набору характеристических корней матрицы Якоби линеаризованной системы можно определить характер поведения фазовых траектории динамических систем процесса в окрестности особой точки, т.е. качественным образом отслеживать поведение процесса. Методы, качественной теории дифференциальных уравнений были применены авторами работ [30-32] для исследования процессов ректификации, а также различных реакционных процессов [77.78, 80].
Ранее в работах [1.2] было показано, что в технологических схемах содержащих ректификацию около 80% всех энергетических затрат приходится именно на этот процесс. Поэтому затраты энергии в реакционно-ректификационных процессах можно оценивать по энергозатратам на ректификацию. Эти затраты в основном связаны с формированием потока пара и для их оценки используют значение минимального флегмового числа, необходимого для получения продуктов заданного качества. Режим минимального орошения реализуется в колонне бесконечной высоты, и при этом в колонне имеются зоны постоянных концентраций [2, 3]. Существуют различные методы оценки минимального флегмового числа как численные, так и аналитические. Численные методы [24.97-104] позволяют определять минимальное флегмовое число для смесей с любым фазовым равновесием и не требуют допущения о постоянстве потоков жидкости и пара по высоте колонны. В их основе лежат уравнения материальных и тепловых балансов для зон постоянных концентраций укрепляющей и исчерпывающей секций ректификационной колонны и различные методики сходимости [25-27.99]. Поскольку численные методы являются итерационными, бывают случаи, когда расчет не сходится. Аналитические же методы позволяют оценить значение минимального флегмового числа непосредственно, однако требуют принятия различных допущений. Наиболее распространенным из таких является метод Андервуда [105-107], в основе которого лежит уравнение, связывающее составы продуктовых потоков со значением минимального флегмового числа при допущениях о постоянных относительных летучестях компонентов разделяемой смеси и постоянстве мольных потоков жидкости и пара по высоте колонны.
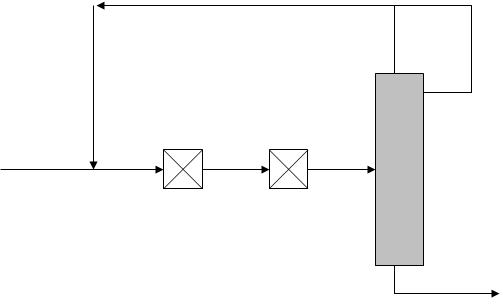
В связи с тем, что в литературе очень мало рассмотрены случаи рециркуляционных реакционно-ректификационных систем с двумя реакторами и, следовательно, варианты организации рециркулирующего потока в таких системах, целью работы является оценка минимальных энергетических затрат в рециркуляционных реакционно-ректификационных процессах с различной организацией подачи рецикла для реакции изомеризации типа А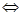 В. В.
В рециркуляционных схемах существуют различные варианты подачи рецикла. В данном случае рассматривается схема, состоящая из двух реакторов и ректификационной колонны. Очевидно, что рецикл может охватывать либо один реактор, либо оба.
Следовательно, нужно рассмотреть оба варианта для выявления наиболее выгодного.
Для успешного поведения анализа необходимо выбрать систему допущений, которая позволяла бы получать с одной стороны содержательные, а с другой стороны – максимально упрощенные модели процессов рециркуляционной реакционно-ректификационной системы.
В связи с этим для описания ректификационного блока разделения будем использовать модели ректификационных колонн, обладающих бесконечной высотой и работающих в режиме бесконечного орошения. Что дает возможность использовать понятия четких и получетких разделений, что предполагает наличие в кубе и дистилляте чистых компонентов. Для описания реакционного узла будет использоваться модель реактора идеального смешения, гидродинамическая модель которого является простейшей. Главным параметром такого реактора является его объем.
Кроме того, будем считать, что рассматриваемые реакции являются каталитическими (протекают только в зоне расположения катализатора) их скорости подчиняются закону действующих масс. Константы скорости прямой и обратной реакции зафиксированы на некоторых постоянных значениях и не зависят от условий проведения процесса.
Проведем анализ систем с различным охватом рецикла.
Рассмотрим рециркуляционную систему (рис.2.1), состоящую из двух реакторов идеального смешения и ректификационной колонны, охваченных обратным рециркулирующим потоком по дистилляту.
RXr
V1 V2
F G L L
XfXgXl1 Xl2
W, Xw
Рис.2.1. Рециркуляционная система.
Реактор-ректификационная колонна с охватом рециклом двух реакторов.
В реакторах протекают обратимые реакции типа A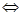 B, скорость которых подчиняется закону действующих масс. На вход в систему подается чистый реагент А, реакционная смесь зеотропна, колонна обладает бесконечной эффективностью по разделению, реагент А является легколетучим компонентом. Тогда в соответствии с обозначениями на рис.2.1. система балансовых уравнений в статике относительно реагента А имеет вид: B, скорость которых подчиняется закону действующих масс. На вход в систему подается чистый реагент А, реакционная смесь зеотропна, колонна обладает бесконечной эффективностью по разделению, реагент А является легколетучим компонентом. Тогда в соответствии с обозначениями на рис.2.1. система балансовых уравнений в статике относительно реагента А имеет вид:
Для смесителя:
G = F + R (2.1)
Gxg = Fxf + Rxr (2.2)
Для колонны:
L = W + R (2.3)
Lxl2 = Wxw + Rxr (2.4)
Для реакторов:
G = L (2.5)
G = F + R (2.6)
Для первого реактора:
Fxf + Rxr = Lxl1 + V1rA1 (2.7)
Где rA1 = k+xl1 – k-(1 – xl1) (2.8)
Для второго реактора:
Lxl1 = Lxl2 + V2rA2 (2.9)
Где rA2 = k+xl2 – k-(1 – xl2) (2.10)
Для системы в целом:
Fxf – Wxw = rA1V1 + rA2V2 (2.11)
Где rA1, rA2 – скорости химической реакции по реагенту А в первом и втором реакторах, V1, V2 – объемы реакционной зоны.
Выразим скорость химической реакции, протекающей в первом реакторе.
Для этого из (2.8) выразим сдержание компонента А на выходе из реактора xl1
Xl1 = 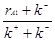 (2.12) (2.12)
И подставим его в выражение (2.7)
Fxf + Rxr - L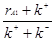 - V1rA1 = 0 (2.13) - V1rA1 = 0 (2.13)
Отсюда, после преобразований:
rA1 = 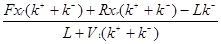 (2.14) (2.14)
С учетом, что L = R + F и что на вход в систему подается чистый компонент А, т.е. xf = 1 и в рецикле тоже чистый компонент А, xr = 1:
rA1 =  (2.15) (2.15)
Отсюда, после преобразований
rA1 =  (2.16) (2.16)
или с учетом, что L = R + F
rA1 = 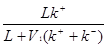 (2.17) (2.17)
Теперь выразим скорость химической реакции, протекающей во втором реакторе:
Содержание компонента А на выходе из реактора
xl2 =  (2.18) (2.18)
Теперь подставляем (2.12) и (2.18) в (2.9):
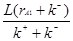 - - 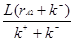 - V2rA2 = 0 (2. 19) - V2rA2 = 0 (2. 19)
после преобразований
rA2 =  (2. 20) (2. 20)
подставим (2.17) в (2. 20):
rA2 = 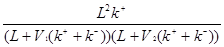 (2.21) (2.21)
Для того чтобы достичь полного превращения сырья производительность реактора должна равняться количеству реагента А, поступающего на вход в систему
F = rA1V1 + rA2V2 (2.22)
Подставим выражения (2.17) и (2.21) в (2.22):
F =  + + 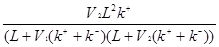 (2.23) (2.23)
После преобразований:
L (k+(V1 + V2) – F) + L(k+ + k-) (V1V2k+ - F(V1 + V2)) – FV1V2(k+ + k-) (k+(V1 + V2) – F) + L(k+ + k-) (V1V2k+ - F(V1 + V2)) – FV1V2(k+ + k-)  = 0 (2.24) = 0 (2.24)
где L = R + F.
Мы получили аналитическое выражение зависимости величины рецикла от объема.
По этому выражению мы можем построить и проследить зависимость величины рецикла от объема реакторов.
Примем k+, k - и F постоянными, а объемы реакторов равными между собой
V1 = V2.
k+ = 2
k - = 1
F = 10кмоль/час.
При этих значениях с помощью программы Excel численно просчитаем, по формуле (2.24), зависимость величины рецикла от объема. Результаты представлены в таблице 2.1.
| R |
V |
V1 |
V2 |
| 58,87981 |
6 |
3 |
3 |
| 21,59592 |
8 |
4 |
4 |
| 14,27051 |
10 |
5 |
5 |
| 11, 20142 |
12 |
6 |
6 |
| 9,539015 |
14 |
7 |
7 |
| 8,50905 |
16 |
8 |
8 |
| 7,815321 |
18 |
9 |
9 |
| 7,320508 |
20 |
10 |
10 |
| 5,672232 |
40 |
20 |
20 |
| 5,324409 |
60 |
30 |
30 |
| 5, 191836 |
80 |
40 |
40 |
| 5,126946 |
100 |
50 |
50 |
| 5,090286 |
120 |
60 |
60 |
| 5,067531 |
140 |
70 |
70 |
| 5,052428 |
160 |
80 |
80 |
| 5,041888 |
180 |
90 |
90 |
| 5,03424 |
200 |
100 |
100 |
| 5,028513 |
220 |
110 |
110 |
| 5,024113 |
240 |
120 |
120 |
| 5,020659 |
260 |
130 |
130 |
| 5,017898 |
280 |
140 |
140 |
| 5,015657 |
300 |
150 |
150 |
| 5,013811 |
320 |
160 |
160 |
| 5,012274 |
340 |
170 |
170 |
| 5,010981 |
360 |
180 |
180 |
| 5,009881 |
380 |
190 |
190 |
Таблица 2.1. Численная зависимость величины рецикла от суммарного объема реакторов при подаче рецикла на вход первого реактора.
По этим данным строится график, представленный на рис.2.2. Рис.2.2. Зависимость величины рецикла от суммарного объема реакторов при подаче рецикла на вход первого реактора.
Из графика видно, что с увеличением рецикла объем уменьшается и наоборот.
Поэтому для проведения какого-либо процесса следует выбирать оптимальное соотношение объема и величины рецикла.
Рассмотрим рециркуляционную систему (рис.2.2), состоящую из двух реакторов идеального смешения и ректификационной колонны, где рецикл охватывает только один реактор.
В реакторах протекают обратимые реакции типа A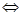 B, скорость которых подчиняется закону действующих масс. На вход в систему подается чистый реагент А, реакционная смесь зеотропна, колонна обладает бесконечной эффективностью по разделению, реагент А является легколетучим компонентом. Тогда в соответствии с обозначениями на (рис.2.3) система балансовых уравнений в статике относительно реагента А имеет вид: B, скорость которых подчиняется закону действующих масс. На вход в систему подается чистый реагент А, реакционная смесь зеотропна, колонна обладает бесконечной эффективностью по разделению, реагент А является легколетучим компонентом. Тогда в соответствии с обозначениями на (рис.2.3) система балансовых уравнений в статике относительно реагента А имеет вид:
Для смесителя:
G = F + R (2.25)
Gxg = Fxf1 + Rxr (2.26)
R Xr
V1 V2
F F G L
Xf Xf1 Xg Xl2
W, Xw
Рис.2.3. Рециркуляционная система. Реактор-ректификационная колонна.
С охватом рециклом одного реактора.
Для колонны:
L = W + R (2.27)
Lxl2 = Wxw + Rxr (2.28)
Для реакторов:
Для первого реактора:
Fxf = Fxf1 + V1rA1 (2.29)
Где rA1 = k+xf1 – k-(1 – xf1) (2.30)
Для второго реактора:
G = F + R (2.31)
Fxf1 + Rxr = Lxl2 – V2rA2 (2.32)
Где rA2 = k+xl2 – k-(1 – xl2) (2.33)
Для системы в целом:
Fxf – Wxw = rA1V1 + rA2V2 (2.34)
Где rA1, rA2 – скорости химической реакции по реагенту А в первом и втором реакторах, V1, V2 – объемы реакционной зоны.
Выразим скорость химической реакции, протекающей в первом реакторе.
Для этого из (2.30) выразим сдержание компонента А на выходе из реактора xf1
Xf1 = 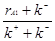 (2.35) (2.35)
И подставим его в выражение (2.29), принимая, что на вход в систему подается чистый компонент А, xf = 1:
F – 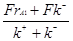 – V1rA1 = 0 (2.36) – V1rA1 = 0 (2.36)
После преобразований:
rA1 = 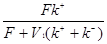 (2.37) (2.37)
Теперь выразим скорость химической реакции, протекающей во втором реакторе:
Содержание компонента А на выходе из реактора
xl2 = 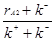 (2.38) (2.38)
Подставим (2.38) и (2.35) в (2.32), принимая, что в рецикле чистый компонент А, xr = 1:
 (2.39) (2.39)
После преобразований
rA2 = 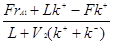 (2.40) (2.40)
затем, подставляя (2.37), получим выражение для скорости химической реакции во втором реакторе:
rA2 = 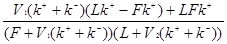 (2.41) (2.41)
Для того чтобы достичь полного превращения сырья производительность реактора должна равняться количеству реагента А, поступающего на вход в систему
F = rA1V1 + rA2V2 (2.42)
Подставим выражения (2.37) и (2.41) в (2.42):
F = 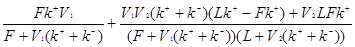 (2.43) (2.43)
После преобразований
L =  (2.44) (2.44)
где L = R + F.
Мы получили аналитическую зависимость величины рецикла от объема реакторов.
По этому выражению мы можем построить и проследить зависимость величины рецикла от объема реакторов.
Примем k+, k - и F постоянными, а объемы реакторов равными между собой
V1 = V2.
k+ = 2
k - = 1
F = 10кмоль/час. При этих значениях с помощью программы Eсxel численно просчитаем, по формуле (2.44), зависимость величины рецикла от объема. Результаты представлены в таблице 2.2.
| V1 |
V2 |
V |
R |
| 4 |
4 |
8 |
63,33333 |
| 5 |
5 |
10 |
27,5 |
| 7 |
7 |
14 |
14,65909 |
| 10 |
10 |
20 |
10 |
| 20 |
20 |
40 |
6,8 |
| 30 |
30 |
60 |
6,071429 |
| 40 |
40 |
80 |
5,757576 |
| 50 |
50 |
100 |
5,584416 |
Продолжение.
| 60 |
60 |
120 |
5,475113 |
| 70 |
70 |
140 |
5,4 |
| 80 |
80 |
160 |
5,345269 |
| 90 |
90 |
180 |
5,303644 |
| 100 |
100 |
200 |
5,270936 |
| 110 |
110 |
220 |
5,244565 |
| 120 |
120 |
240 |
5,222857 |
| 130 |
130 |
260 |
5, 204678 |
| 140 |
140 |
280 |
5,189235 |
| 150 |
150 |
300 |
5,175953 |
| 160 |
160 |
320 |
5,16441 |
| 170 |
170 |
340 |
5,154286 |
| 180 |
180 |
360 |
5,145334 |
| 190 |
190 |
380 |
5,137363 |
| 200 |
200 |
400 |
5,130219 |
| 210 |
210 |
420 |
5,123781 |
| 220 |
220 |
440 |
5,117949 |
| 230 |
230 |
460 |
5,112641 |
| 240 |
240 |
480 |
5,10779 |
| 250 |
250 |
500 |
5,103339 |
Таблица 2.2. Численная зависимость величины рецикла от суммарного объема реакторов при подаче рецикла на вход второго реактора. График по этим данным представлен на рис 2.4.
Рис.2.4. Зависимость величины рецикла от суммарного объема реакторов при подаче рецикла на вход второго реактора.
По графику видно, что с увеличением объема рецикл уменьшается и наоборот.
Концы кривой стремятся к некому пределу. Если взять, например, объем меньше предельной величины, то ни при какой величине рецикла 100% -ая конверсия не может быть достигнута.
С помощью пакета программ ChemCad проверяем аналитические расчеты и зависимости.
Эта программа, как и множество других, с успехом используется для решения многочисленных задач, связанных с анализом и синтезом ХТС, основными элементами которых являются реакционные и массообменные аппараты.
Проведем анализ двух рециркуляционных реакционно-ректификационных систем с различной подачей рецикла, но при одинаковых начальных условиях.
Сначала проверим зависимость величины рецикла от суммарного объема с помощью опытных данных снятых в программе ChemCad.
В обеих системах протекает одна и та же реакция изомеризации параксилола в ортоксилол. Начальный поток F=10 кмоль/час содержит только чистый параксилол, xf=1. Ректификационная колонна содержит 70 тарелок. Тарелка питания №35, паровое число Rb=50.
Рассчитаем минимальный суммарный объем реакторов по формуле
Vmin = 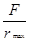 = = 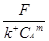 (3.1) (3.1)
Где CAm = rA, при температуре реакции (t=1000C=3730K),
Где плотность считается по формуле, представленной в программном пакете ChemCad 5.2.
rA =  (3.2) (3.2)
Коэффициенты для параксилола:
А = 0,67752
В = 0,25887
С = 616,2
D = 0.27596
Следовательно r = 2,98, а Vmin = 1,68м3, при k+= 2 и F = 10кмоль/час.
Для схемы с рециклом, охватывающим два реактора зависимость выглядит следующим образом (таблица 3.1): данные сняты при постоянном составе смеси в кубовой части колонны – содержание параксилола x=0.001м. д.
| V, м3 |
R, кмоль/час |
| 8 |
6,2 |
| 7 |
6,3 |
| 6 |
6,5 |
| 5 |
6,9 |
| 4 |
7,7 |
| 3 |
11,1 |
| 2,5 |
12,1 |
| 2 |
13,55 |
| 1,7 |
15,6 |
| 1,68 |
15,7 |
Таблица 3.1. Численная зависмиость величины рецикла от суммарного объема реакторов при охвате рециклом двух реакторов при постоянном составе х=0,001м. д.
Графическая зависимость по данным таблицы 3.1. представлена на рис. (3.1) Рис.3.1. Зависимость величины рецикла от суммарного объема реакторов при подаче рецикла на вход первого реактора при постоянном составе смеси.
Для схемы с рециклом, охватывающим один реактор зависимость выглядит следующим образом (таблица3.2): данные сняты при постоянном составе смеси в кубовой части колонны – содержание параксилола x=0.001м. д.
| V, м3 |
R, кмоль/час |
| 8 |
7,5 |
| 7 |
7,8 |
| 6 |
8,5 |
| 5 |
11 |
| 4 |
13,2 |
| 3 |
13,5 |
| 2,5 |
15,9 |
| 2,2 |
16,3 |
| 2 |
19,5 |
Таблица 3.2. Численная зависимость величины рецикла от суммарного объема реакторов при подаче рецикла на вход второго реактора при постоянном составе х=0,001м. д.
График, по этим данным, представлен на рис.3.2.
Рис.3.2. Зависимость величины рецикла от суммарного объема реакторов при подаче рецикла на вход второго реактора при постоянном составе х=0,001м. д. Из этих графиков (рис.2.2, 2.4, 3.1. и 3.2) видно, что вид зависимостей, полученных аналитически и рассчетно, совпадает. Прослеживается одна и та же закономесрность. С увеличением рецикла объем уменьшается и наоборот.
Теперь построим зависимости энергозатрат от величины рецикла, при постоянном составе смеси в кубе колонны, содержащей x=0.001м. д. параксилола, и суммарном объеме V=5м3:
Для схемы с рециклом, охватывающим два реактора численная зависимость представлена в таблице 3.3.
| R, кмоль/час |
Rb |
Q*107, кДж/час |
| 7 |
48 |
1,79177 |
| 8 |
43 |
1,60518 |
| 9 |
43 |
1,60509 |
| 10 |
43 |
1,60514 |
| 11 |
45 |
1,67978 |
| 12 |
45 |
1,67982 |
| 15 |
48 |
1,79183 |
| 20 |
53 |
1,97834 |
| 25 |
58 |
2,16508 |
| 30 |
63 |
2,35169 |
| 35 |
68 |
2,53832 |
| 40 |
73 |
2,72503 |
| 45 |
78 |
2,91184 |
| 50 |
83 |
3,09846 |
| 55 |
88 |
3,28511 |
| 60 |
93 |
3,47152 |
| 65 |
98 |
3,65804 |
| 70 |
103 |
3,84471 |
| 75 |
108 |
4,03104 |
| 80 |
113 |
4,21836 |
| 85 |
117 |
4,36775 |
| 90 |
122 |
4,55428 |
| 95 |
127 |
4,74097 |
| 100 |
132 |
4,92748 |
Таблица 3.3. Численная зависимость энергозатрат от величины рецикла при постоянном составе х=0,001м. д. и суммарном объеме реакторов V = 5м3 при подаче рецикла на вход первого реактора.
График представлен на рис.3.3.
Рис.3.3. Зависимость энергозатрат от величины рецикла при постоянном составе х=0,001м. д. и суммарном объеме реакторов V = 5м3 при подаче рецикла на вход первого реактора.
По графику видно, что при наращивании рецикла, энергозатраты увеличиваются, сначала походя через некоторый минимум, который соответствует оптимальной величине рецикла.
Для схемы с рециклом, охватывающим один реактор численная зависимость выглядит следующим образом (таблица 3.4):
| R, кмоль/час |
Rb |
Q*107, кДж/час |
| 7,5 |
81 |
3,02356 |
| 8 |
60 |
2,23976 |
| 9 |
50 |
1,86656 |
| 10 |
50 |
1,86636 |
| 11 |
50 |
1,86646 |
| 12 |
50 |
1,86641 |
| 15 |
51 |
1,90376 |
| 20 |
55 |
2,05305 |
| 25 |
60 |
2,23976 |
| 30 |
65 |
2,42644 |
| 35 |
70 |
2,61309 |
| 40 |
75 |
2,79947 |
| 45 |
79 |
2,94901 |
| 50 |
85 |
3,17299 |
| 55 |
89 |
3,32223 |
| 60 |
95 |
3,54617 |
| 65 |
99 |
3,69527 |
| 70 |
105 |
3,91953 |
| 75 |
109 |
4,06921 |
Продолжение.
| 80 |
115 |
4,29231 |
| 85 |
119 |
4,44231 |
| 90 |
125 |
4,66578 |
| 95 |
129 |
4,81576 |
| 100 |
135 |
5,03959 |
Таблица 3.4. Численная зависимость энергозатрат от величины рецикла при постоянном составе х=0,001м. д. и суммарном объеме V = 5м3 при подаче рецикла на вход второго реактора.
Графическая зависимость представлена на рис.3.4.
Рис.3.4. Зависимость энергозатрат от величины рецикла при постоянном составе х=0,001м. д. и суммарном объеме V = 5м3 при подаче рецикла на вход второго реактора. На рис.3.4. прослеживается почти такая же зависимость как и на рис.3.3. только различаются минимумами знергозатрат. В схеме с охватом рециклом двух реакторов минимум находится ниже (энергозатраты меньше).
Обсуждение результатов.
Для того, что бы проследить отличия в схемах с различным охватом рециклом, построим совместные графики.
На рис.3.5. представлена зависимость величины рецикла от суммарного объема реакторов, построенная по результатам количественного анализа. Рис.3.5. Зависимости величины рецикла от суммарного объема реакторов при различном охвате рециклом реакторов.
По графику видно, что при больших величинах рецикла или объема обе зависимости очень близки, а при малых величинах рецикла или объема зависимости отдаляются друг от друга. Например, при фиксированном суммарном объеме реакторов V = 300м3, величина рецикла в системе с охватом рециклом двух реакторов R = 5,015657 кмоль/час, а с охватом одного реактора R = 5,175953 кмоль/час. А при суммарном объеме реакторов V=10м3, величины рецикла соответственно равны 14,27051 и 27,5 кмоль/час. Причем, схема, в которой рецикл охватывает два реактора, оказывается выгоднее, чем схема, в которой рецикл охватывает один реактор.Т. к. в первой при малых величинах суммарного объема реакторов требуется меньшая величина рецикла, для достижения заданной конверсии, чем во второй.
Теперь строим совместный график зависимостей величины рецикла от суммарного объема реакторов при различной подаче рецикла по расчетным данным, полученным в программе ChemCad. В обеих системах протекает одна и та же реакция изомеризации параксилола в ортоксилол. Начальный поток F=10 кмоль/час содержит только чистый параксилол, xf=1. Ректификационная колонна содержит 70 тарелок. Тарелка питания №35, паровое число Rb=50.
График представлен на рис.3.6. Рис.3.6. Зависимость величины рецикла от суммарного объема реакторов при различной подаче рецикла, при поддержании заданной селективности.
По этому графику ярче видны различия двух схем, т. к. рассматривается та часть графика, где эти две прямые наиболее отличаются друг от друга. Здесь явно видно, что в схеме с охватом рециклом двух реакторов при некотором фиксированном значении суммарного объема реакторов требуется меньшая величина рецикла для достижения заданной конверсии (и наоборот, при некоторой фиксированной величине рецикла требуется меньший суммарный объем реакторов), чем в схеме с охватом рециклом одного реактора.
Теперь построим совместный график зависимостей энергозатрат от величины рецикла при различной организацией подачи рецикла.
График, представленный на рис.3.7, построен по расчетным данным, взятым из программы ChemCad. Начальные условия такие же как при построении графика 3.6. В обеих системах протекает одна и та же реакция изомеризации параксилола в ортоксилол. Начальный поток F=10 кмоль/час содержит только чистый параксилол, xf=1. Ректификационная колонна содержит 70 тарелок. Тарелка питания №35, паровое число Rb=50.
График построен при постоянном составе смеси в кубе колонны, содержащей x=0.001м. д. параксилола, и суммарном объеме реакторов V=5м3.
Рис.3.7. Зависимость энергозатрат от величины рецикла при различной организации подачи рецикла.
По графику видно, что энергетически более выгодная схема с охватом рециклом двух реакторов, т. к. при фиксированной величине рецикла в ней энергозатраты меньше по сравнению со схемой с охватом рециклом одного реактора. И оптимальная величина рецикла требует меньших энергетических затрат в системе с подачей рецикла на вход первого реактора. Например, при фиксированной величине рецикла R=10 кмоль/час, энергозатраты в системе с охватом рециклом двух реакторов Q=1,60514*107кДж/час, а в системе с охватом рециклом одного реактора Q=186636*107кДж/час.
Проведен анализ стационарных состояний реакционной схемы для реакции типа А Û В при различных вариантах организации подачи рецикла.
Показана возможность достижения практически полного превращения реагента в рециркуляционной схеме, как при подаче рецикла на вход первого реактора, так и на вход второго.
Для различных вариантов организации подачи рецикла определены области в пространстве величин потока рецикла и объема реактора, при которых возможна 100% -ая конверсия.
Проведена оценка минимальных энергетических затрат, необходимых для достижения заданной конверсии в рециркуляционных схемах с двумя реакторами и ректификационной колонной в случаях различной организации подачи рецикла.
1. Тимофеев B. C. Серафимов Л.А., Принципы технологии основного органического и нефтехимического синтеза: Учебное пособие для вузов. - М.: Химия. 1992.
2. Жаров ВТ., Серафимов Л.А. . Физико-химические основы дистилляции и ректификации. Л. Химия, 1974, 239 с.
3. Петлюк Ф.Б., Серафимов Л.А. Многокомпонентная ректификация. Теория и расчет. М., Химия, 1983.
4. Тимофеев В. С, Серафимов Л.А., Писаренко Ю.А., Солохин А.В. Технология основного органического синтеза. Совмещенные процессы. М.: Химия, 1993.
5 Лебедев Н.Н., Манаков М.Н., Швец В.Ф., Теория технологических процессов основного органического и нефтехимического синтеза, М., Химия, 1975, с.478.
6. Плановский А.Н., Химическая промышленность, 1944, №5-6, с.5.
7. Нагиев М.Ф. Теоретические основы рециркуляционных процессов в химии. - М.: Изд-во Акад. Наук. 1962. с.31.
8. Нагиев М.Ф. Этюды о химических системах с обратной связью. М., Наука, 1971, 92 с.
9. Нагиев М.Ф. Химическая рециркуляция. - М.: Наука. 1978.
10. Кафаров В.В. Принципы создания безотходных химических производств М.: Химия. 1982.
11. Kiss S. A. Ind. Eng. Chem., 1930, v 22, №1 с.10.
12. Маркович И.Б. Труды I Всесоюзного съезда ВНИТО нефтяников, М., Грозный, Новосибирск, ОНТИ НКТП СССР, 1934, с.283.
13. Дуев С. И, Бояринов А.И., Кафаров В.В. Исследование режимов с полным использованием исходных и промежуточных реагентов в системе реактор-узел разделения. Сб. Системный анализ процессов химической технологии. М: МХТИ, 1979. Вып.106. С.96.
14. Дуев С. И, Бояринов А.И. Исследование реакторных систем с рециклом. Известия ВУЗов СССР. Химия и хим. технол. 1980. №6. С.776.
120
15. Дуев С.И. . Теория рециркуляционной схемы реактор-блок разделения: Дис. докт. техн. наук. М.: МХТИ, 1993.
16. Дуев С.И., Бояринов А.И. Явление температурной неоднозначности в рециркуляционной системе реактор-блок разделения. // Теор. основы хим. технол. 1998. Т.32. №5. С.524.
17. Бояринов А.И., Дуев АИ. Анализ стационарных состояний реактора идеального вытеснения с рециклом. // Теор. основы хим. технол., 1988, т.22, №4, с.402-404.
18. Бояринов АИ., Дуев А.И. Расчет параметров реактора идеального смешения с рециклом для обратимой реакции второго порядка. // Теор. основы хим. технол., 1995, т.29, №4, с.441.
19. Кафаров ВВ., Дорохов И.Н., Системный анализ процессов химической технологии, М., Наука, 1976.
20. Кафаров В.В., Дорохов И.Н., Кольцова Э.М., Системный анализ процессов химической технологии, М., Химия, 1983.
21. Кафаров ВВ., Дорохов И.Н. Системный анализ процессов химической технологии. Топологический принцип формализации. М., Наука, 1979, 399 с.
22. Солохин А.В. Системный анализ рециркуляционных и совмещенных реакционно-ректификационных процессов. Дисс. докт. техн. наук: - М., МИТХТ, 1996.
23. Солохин А.В., Благов/ С.А., Тимофеев В.С. Качественный анализ реакционно-ректификационных схем // Теор. основы хим. технол. 1996 т.30. №2. С.151.
24. Чарльз Д. Холланд. Многокомпонентная ректификация, М., Химия, 1969
25. Rose A., Sweeny R. F., Scrodt V. N. Continious Distillation Calculation by Relaxation Method // Ind. Eng. Chem. - 1958. - V.50. - No5. - P.737-740.
26. Komatsu H., Holland Ch. D. A new method of convergence for solving reacting distillation problems // Journal of chemical engineering of Japan. - 1977. - V.10. - No4. - P.292 - 297.
27. Chang J. A., Seader J. D. Simulation of continuous reactive distillation by a homotopy continuation method // Computers & Chem. Engineering. - 1988. - V. 12. -No 12. -P.1243 - 1255.
28. Б.Н. Баутин, Е.А. Леонтович Методы и приемы исследования динамических систем на плоскости.М. Наука Физматлит 1990.
29. Мозжухин АС, Митропольская В.А., Тихонова Н.К. Анализ структур диаграмм парожидкостного равновесия // Учебн. пособие, МИТХТ, 1988.
30. Готлиб В. А, Митропольская В.А., Мозжухин А.С. Анализ эволюции фазовых портретов динамических систем ректификации. // Теор. основы хим. технол., т.27, №5, 1993, с.489-494.
31. Митропольская В.А., Мозжухин А.С. Исследование динамических систем ректификации при наличии нулевых концентраций в продуктах // Физико-химические основы ректификации, Сб тр. МИТХТ, М., МИХМ, 1977,. с.118-130.
32. Митропольская В.А. Кандидатская диссертация.М. МИТХТ 1977.
33. Мозжухин А. С, Митропольская В.А. О стыковке траекторий ректификации в колоннах бесконечной эффективности // Физико-химические основы ректификации, М, МИХМ, 1977, с.131-137.
34. Карапетьянц М.Х., Химическая термодинамика, М., Химия, 1975
35. Серафимов Л.А., Фролкова А.К. Фундаментальный принцип перераспределения полей концентраций между областями разделения как основа создания технологических комплексов // Теор. основы хим. технол. т.31, №2, 1997, с.184-192.
36. Серафимов Л.А., Писаренко Ю.А., Тимофеев B. C. Реакционно-массообменные процессы: проблемы и перспективы. // Теор. основы хим. технол. 1993. Т.27. № 1. С.4-13.
37. Солохин А.В., Благов С.А., Серафимов Л.А., Тимофеев ВС. Исследование динамической системы процесса открытого испарения при наличии химической реакции А о В. // Теор. основы хим. технол. 1990. Т.24. № 5 С.579-584.
38. Солохин А.В., Благов С. А, Тимофеев B. C., Серафимов Л.А. Качественный анализ реакционно-ректификационного процесса с нелокализованной реакционной зоной // Теор. основы хим. технол. - 1993. - Т.27. - №5. - С 478 - 488.
122
39. Балашов М.И. . Патласов В.П. . Серафимов Л.А. Правила принципиальной протяженности реакционной зоны в непрерывных совмещенных реакционно-ректификационных процессах: Теор. основы хим. технол. - 1980. - .14. - №5. - С.650-658
40. Патласов В.П. Качественные методы исследования реакционно-ректификационных процессов и разработка промышленных совмещенных процессов получения органических продуктов: Дис. докл. техн. наук. - М. . 1996.
41. Балашов М.И. . Серафимов Л.А. Анализ статики непрерывных совмещенных реакционно-ректификационных процессов Теорет. основы хим. технол. - 1980. - Т.14. -№6. -С.803-808.
42. Балашов МИ. Физико-химические основы и технологические принципы организации реакционно-ректификационных процессов: Дис. докт. техн. наук. - М. 1980. - 564 с.9.
43. Писаренко Ю.А. . Данилов Р.Ю. Выделение предельных стационарных состояний реакционно-ректификационных процессов // В кн.: Ш международная конференция "Наукоемкие химические технологии". Тезисы докладов - Тверь. 1995. - С.37 - 38.
44. Писаренко Ю.А. . Данилов Р.Ю. . Серафимов Л.А. Возможные виды разделения в непрерывных совмещенных реакционно-ректификационных процессах // Теор. основы хим. технол. 1996. - Т.30. -№6. -С.641 - 649.
45. Писаренко Ю.А. Разработка теоретических основ анализа стационарных режимов реакционно-массообменных процессов. Дис... . докт. техн. наук. - М, МИТХТ. 1998.
46. Гарбер Н.Ю. Анализ статики непрерывных совмещенных реакционно-ректификационных процессов с помощью ЭВМ. Автореф. дис... . канд. техн. наук. - М. 1983. - 21 с.
47. Савченко В.П. . Гельперин Н.И. Метод расчета реакционно-ректификационных аппаратов, Теор. основы хим. технол. - 1972. - Т.6, - №5. - С.748-755. 123.
48. Barbosa D., Doherty F. M. Design and minrmiim-reflux calculations for double-feed multicomponent reactive columns. // Chem. Eng. Sei. 1988. V.43. No.9. - P.2377-2389.
49. Okasinski M. J., Doherty M. F. Design Method for Kinetically Controlled, Staged Reactive Distillation Columns. // Ind. Eng. Chem. Res. 1998. V.37. p.2821-2834.
50. Grosser J. H., Doherty M. F., Malone M. F. Modelling of reactive distillation systems // Ind. Eng. Res. - 1987. - V.26. P. -983 - 989.
51. Syzulyi 1, Yagi H., Komatsy H., Hirata M. Calculation of multicomponent distillation accompanied by a chemical reaction // Journal of chemical engineering of Japan - 1971, - V.4. - Nol - P.26 - 33.
52. Komatsu H. Application of the relaxation method for solving reacting distillation problems // Journal of chemical engineering of Japan. - 1977. - V.10. - No 3. -P. 200 - 205.
53. Балашов М.И. Исследование совмещенного реакционно-ректификационного процесса на примере гидролиза метилацетата: Дис... . канд. техн. наук.М., 1967. -246 с.
54. Патласов В.П., Коровина Т.В., Балашов М.И. Экспериментальное исследование реакционно-ректификационного процесса получения пропилацетата // Гидролизная и лесохимическая промышленность. - 1985. - №4. - С.4-5.
55. Жучков В.И. Разработка малоотходной технологии производства бутилацетата этерификацией уксусной кислоты: Дис. канд. техн. наук. - М., 1985.
56. Епифанова О.А. Стационарные состояние непрерывных совмещенных реакционно-ректификационных процессов (на примере технологии получения бутилацетата): Дис... . канд. техн. наук. - М., 1988. - 180 с.
57. Синегуб В.В. Разработка технологии получения аллилового спирта из аллилацетата в непрерывном совмещенном реакционно-ректификационном процессе: Дис. канд. техн. наук. - М., 1993. - 300 с.
58. Голикова Т.Н. Исследование непрерывного реакционно-ректификационного процесса получения этилацетата: Дис. канд. техн. наук. - М., 1975. - 172 с.
59. Анохина Е.А., Кардона К.А., Писаренко Ю.А., Саксонова О.И., Пономарев В.Н. Основные этапы разработки совмещенных процессов на примере НСРРП получения аллилового спирта бутанолизом аллилацетата Часть 1. Выбор варианта организации совмещенного получения аллилового спирта // Химическая промышленность. - 1996. - №9. - С.689 - 693.
60. Анохина Е.А., Кардона К.А., Писаренко Ю.А., Саксонова О.И., Пономарев В.Н. Основные этапы разработки совмещенных процессов на примере НСРРП получения аллилового спирта бутанолизом аллилацетата Часть 2. Разделение реакционной смеси, отводимой из реакционно-ректификационной колонны синтеза аллилового спирта // Химическая промышленность. - 1996. - №11. -С.537-543.
61. Фролова Е.И. Разработка совмещенного процесса получения этилформиата: Дис... . канд. техн. наук. . - М., 1992. - 210 с.
62.В.П. Патласов, М.И. Балашов, A. M. Чащин, Л.А. Серафимов, и др. Способ получения этилацетата / А. с.857109 СССР. Заявл.17.07.79; Опубл.23.08.81. Бюлл. №31.
63.М.И. Балашов, Т.Н. Голикова, В.П. Патласов, Ю.А. Писаренко, Л.А. Серафимов, и др. Способ получения этилацетата / А. с.663691 СССР. Заявл.15.09.76; Опубл.25.05.79. Бюлл. № 19.
64. Серафимов, Л.А. Солохин А.В. Математическое обеспечение технологических задач основного органического синтеза. М.А.О. Росвузнаука 1992.
65. Podrebarac G. G., Ng F. T. T., Rempel G,L. More uses for catalytic distillation, CHEMTECH №5 p.37
66. Серафимов Л.А., Балашов М.И. Реакционно-ректификационные процессы // Астарита Дж. Массопередача с химической реакцией. Л.: Химия, 1971. Гл.17. -С.186-215.
67. Amy R. Ciric, Deyao Gu, "Synthesis of Nonequilibrium Reactive Distillation Processes by MINLP Optimization". Dept. Of Chemical Engineering, University of Cincinati, Cincinnati, OH 45221., 1994, AIChE Journal.
68. Благов С.А. Разработка метода анализа стационарных состояний рециркуляционных реакционно-ректификационных процессов. Дисс... . канд. техн. наук, М, МИТХТ, 1999.
69. Naphtali L. M., Sandholm D. P. Multicomponent separations calculations by linearization // AlChE. - 1971. -V.17. -P.148.
70. Патласов В.П. Исследование реакционно-ректификационных процессов на примерах алкоголиза метилацетата: Дис... . канд. техн. наук. - М., 1977. -160 с.
71. Патласов В.П., Балашов М.И., Чеботаев В.Ф., Получение бутилацетата из метилацетата и бутанола переэтерификацией, совмещённой со специальными методами ректификации // Гидролиз, и лесохим. пром-ть, 1984, №3, с.8-11.
72. Лебедев Н.Н., Химия и технология основного органического и нефтехимического синтеза, М., Химия, 1971.
73. Павлов С.Ю., Горшков В.А., Смирнов В.А. Получение метилтретбутилового эфира и других высокооктановых эфиров // Химическая промышленность. - 1991. -№5. -С.7-9.
74.А. С.278817 СССР, МКИ3 С07С 41/00. Способ получения 2-метоксипропена // Юркина ОТ., Захарова Й.Н., Миропольская М.А., Самохвалов Г.И. (СССР). -1969. -Н/П.
75. Калерин Е.А. Системный анализ реакционно-ректификационных процессов (на примере получения 2 - метоксипропена): Дис. канд. техн. наук., М., МИТХТ 1987.
76. Солохин А.В., Благов С.А., Тимофеев B. C. Технологические схемы, использующие принцип перераспределения полей концентраций за счет химической реакции // Теор. основы хим. технол. т.31, №2, 1997, с. 193-201.
77. Франк-Каменецкий Д.А. Диффузия и массопередача в химической кинетике, М., Наука, 1967.
78. Перлмуттер Д. Устойчивость химических реакторов, Л., Химия 1976.
79. Левеншпиль О. Инженерное оформление химических процессов, М., 1969.
80. Арис Р., Анализ процессов в химических реакторах, - Л., Химия, 1967.
81. Пономарев В.Н., Саксонова О.И., Тимофеев B. C. Полистационарность б процессах непрерывной ректификации. // Теор. основы, хим. технол. 1996. т.30. №4. -с.383.
82. Kienle A. . Gilles ED Computing Multiple Steady States in Homogeneous Azeotropic Distillation Processes. / Сотр. Chem. Engng. 1994. V.18. Suppl. P. S37-S41.
83. Bekiaris N. . Meski G. A. . Radu СМ. . Mbrari M. Multiple Steady States in Homogeneous Azeotropic Distillation. Ind. Eng. Che. . Res. 1993. V.32, No.9. p. 2023-2038.
84. Bekiaris N. . Meski СМ. . Morari M. Multiple Steady States in Heterogeneous Azeotropic Distillation. Ind. Eng. Che. . Res. 1996. V.35, No. l. p. 207-227.
85. Bekiaris N. . Morari M. Multiple Steady States in Distillation; x/x Predictions. Extensions and Implications for Design. Synthesis and Simulation // Ind. Eng. Chem. Res. 1996. v.35. Noll. - p.4264.
86. Мозжухин А.С. Сеченых АИ. Полистационарность в непрерывной ректификации и реализация выбранного стационарного состояния. // Ученые записки МИТХТ. вып.1. 1999. с.70-75.
87. Chavez R. C. Seader J. D. . Waybum T. L. Multiple Steady-State Solutions for Interlinked Separation Systems. It Ind. Engng. Chem. Fundam. 1986. v.25. - p.566.
88. Тимофеев B. C. . Солохин А В. . Калерин Е.А. Полистационарные состояния в реакционно-ректификационном процессе // Теор. основы хим. технол. - 1988. - т.22. - №6. - С.729-733.
89. Писаренко Ю.А. . Серафимов Л.А. Стационарные состояния процесса дистилляции с химической реакцией. // Теор. основы хим. технол. 1991. т.25, №3. с.422-426.
90. Писаренко Ю.А. . Анохина Е.А. . Серафимов Л.А. Поиск множества стационарных состояний противоточных реакционно-массообменных процессов // Теор. основы хим. технол. - 1993. - Т.27. - №6. С.586 - 590.
91. Писаренко ЮА. . Епифанова О.А. . Серафимов Л.А. Стационарные режимы одноотборньгх реакционно-ректификационных процессов // Теор. основы хим. технол. - 1987. - Т.21. - №4. - С.466 - 469.
92. Ciric A. R. . Miao P. Steady-State Multiplicities in an Ethvlene GKcol Reactive Distillation Column. // Ind. Eng. Chem. Res. 1994. v.33. - p.2738.
93. Jacobs R. . Krishna R. Multiple Solutions in Reactive Distillation for Methyl tert-Butyl Ether Synthesis. // hid. Eng. Chem. Res. 1993. v.32. - p.2438.
94. NijhutS S. A. . Kakhof F. P. J. M., Мак AN S. Multiple Steady States During
Reactive Distillation of Methyl tert-Butyl Ether // lnd. Eng. Chem. Res. 1993. v.32. -p.2767.
95. Hauan S. . Heitzberg Т. . Lien KM. Why MTBE Production by Reactive Distillation May Yield Multiple Solutions - // lnd. Eng. Chem. Res. 1995. V.34. p.987.
96. Солохин А.В. . Благов С.А. . Тимофеев B. C. Анализ энергетических затрат в системах с селективным обменом веществом с окружающей средой /У Теор. основы хим. технол. . т.31. №1. 1997. с.56-61.
97. Кафаров ВВ. . Ветохин В.Н. . Бояринов АИ. Программирование и вычислительные методы в химии и химической технологии. - М.: Наука. 1972. с.486.
98. Ортега Дж. . Рейнболт В. Итерационные методы решения нелинейных уравнений со многими неизвестными - М. . Мир. 1975. - 558 с.
99. Hirose Y. . Tsuba M. Straighforward determination of attenuation factor and treatment of nonphysical values for the Newton-Raphson method - an applicaton to distillation system /'/ Journal of chemical engineering of Japan. - 1978. - V.11. -No2. P.102-106.
100. Broyden C. G. A class of methods for solving nonlinear simultaneous equations II Mathematics of Computation. - 1965. - V, 19. - P.577.
101. Barbosa D. Doherty F. M. Design and minimum-reflux calculations for single-feed multicomponent reactive distillation columns // Chem. Engng. Sci. - 1988.
102. M. Tavana. D. N. Hanson lnd. Eng. Chem. Process Des. & Develop.18 №1 1979 154-156.
103. Shiras R. N. . Hanson D. N... Gibson G. H lnd. Eng. Chem.42 №5 1950 871-876.
104. Bachelor J. B. Petroleum Refiner 36 №6 1957 161-170.
105. Underwood. A. J. V. J. lnst. Petrol.32M946 598-613.
106. Underwood. A. J. V. J. lnst. Petrol.32 1946 614-627.
107. Underwood. A. J. V. Chem. Eng. Progr.44 №8 1948 603-614.
108. Благов С.А. . Солохин А.В. . Клемешова С.А. . Тимофеев ВС Сравнительный анализ системы реактор-колонна и совмещенного реакционно-ректификационного процесса на основе энергетических затрат. //
109. Теор. основы хим. технол., 1995, т.29, № 1, с.15-21.109. Коган Л.М. Производство и переработка окиси этилена в Германии. - М.:
110. Госхимиздат. 1947. С.121. ПО. Дымент О.Н., Казанский К.С., Мирошников A. M. Гликоли и другие производные окисей этилена и пропилена. - М.: Химия. 1976. с.376.
111. Квокенбуш Б., "Хелкон", пат. США №3872164; Получение этиленгликоля через образование эфиров гликоля. 1975. Изобретение стран мира. 1976.
112. Иоффе Б.С., Новикова Т.А., Химическая промышленность. Обзорная информация. Производство этиленгликоля за рубежом, М.: НИИТЭХИМ, 1980, с.36.
113. Гороззи Л., Тилтон ВВ., пат. США №3629343, 1971; приор. Англ. патент №1177877, 1970, Получение этиленгликоля из этиленкарбоната; Изобретения стран мира, 1972.
114. Brownstein A. M. Hydrocarb Process. 1975. v.53. p.129-132.
115. Hydrocarbon Process., 1978, 57, №4, с 166.
116. Монтикото Ниро и др., Япон. заявка №22406, 1973, Катализаторы для процесса гидратации окиси этилена; М., Химия, 1975.
117. Солохин А.В., Благов С.А., Тимофеев В.С. Влияние рецикла на производительность реактора // Теор. основы хим. технол. 1995. т.29. №5. С.528.
118. Henley E. J., Seader J. D. Equilibrium-Stage Separation Operations in Chemical Engineering. JOHN WILEY & SONS. New York, Chichester, Brisbane, Toronto, Singapore.
119. Рид Р., Праузниц Дж., Шервуд Т. Свойства газов и жидкостей, Л., Химия 1982.
120. Назанский С.Л., Солохин А.В., Благов С.А., Тимофеев B. C. Анализ возможных стационарных состояний системы реактор - ректификационная колонна с рециклом для реакции типа А+В<=>С // Теор. основы хим. технол. т.33, № 3, 1999, с.1-7.
121. Назанский С.Л., Благов С.А., Солохин А.В., Тимофеев B. C. Анализ стационарных состояний системы реактор - ректификационная колонна с
рециклом при наличии нескольких химических реакций // Тезисы докладов V Международной конференции "Методы кибернетики химико-технологических процессов" Казань 1999, с 127.
122. Назанский С.Л., Благов С.А., Солохин А.В., Тимофеев B. C. Сравнение системы реактор - ректификационная колонна и совмещенного реакционно-ректификационного процесса с позиции энергетических затрат // Тезисы докладов V Международной конференции "Методы кибернетики химико-технологических процессов" Казань 1999, с 126.
123. Назанский С. Л, Солохин А.В. Стационарные состояния комплекса реактор - ректификационная колонна с рециклом при протекании параллельно-последовательных реакций // Тезисы докладов VI Международной конференции "Наукоемкие химические технологии" Москва 1999, с 109.
124. Назанский С.Л., Благов С.А., Солохин А.В. Анализ минимальных энергетических затрат в совмещенном и рециркуляционном реакционно-ректификационных процессах // Тезисы докладов VI Международной конференции "Наукоемкие химические технологии" Москва 1999, с 116.
125. Назанский С.Л., Солохин А.В., Благов С.А., Тимофеев B. C. Стационарные состояния реакционно-ректификационных процессов на примере реакции типа А+В<=>С // Наука и технология углеводородов № 4, 2000, с.110-115.
126. Bronsted I. N., Kilpatric M., J. Am. Chem. Soc, 1929, v.51, №2, p.428-461.
|