МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
Донбасский государственный технический Университет
Кафедра прикладной механики
Динамический анализ механизмов долбежного станка
Алчевск, 2006
Схема механизма и исходные данные
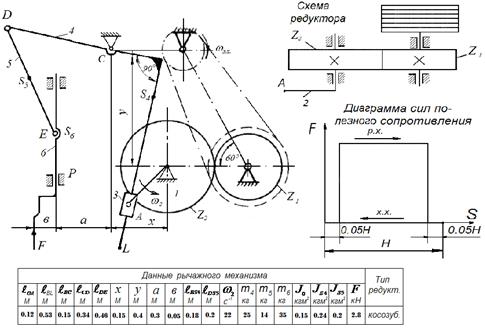
Механизмы долбежного станка
Долбежный станок предназначен для долбления пазов и внутренних канавок в отверстиях. Для движения ползуна с резцом используется шестизвенный кривошипно-кулисный механизм OALBCDEP с качающейся кулисой. Кривошип 2 получает вращательное движение от электродвигателя через клинно-ременную передачу и горизонтальный одноступенчатый редуктор с цилиндрическими колесами. Вращательное движение кривошипа преобразуется в возвратно-поступательное движение ползуна 6 через качающуюся вокруг опоры С кулису 4 с камнем 3 и шатун 5. Ход ползуна Н выбирается в зависимости от длины обрабатываемой поверхности детали с учетом перебегов 0.05Н в начале и конце рабочего хода (см. диаграмму сил полезного сопротивления). Рабочий ход ползуна 6 совершается за больший промежуток времени, чем холостой ход, и соответствует большему углу поворота кривошипа.
Кинематический анализ и выбор электродвигателя
Планы положения мех – ма и силы полезного сопротивления
Выбрав масштаб  построили 8–9 планов положений механизма при общем изображении стойки. Пусть ОА=35 мм, тогда построили 8–9 планов положений механизма при общем изображении стойки. Пусть ОА=35 мм, тогда
 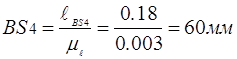
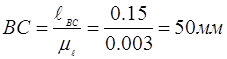 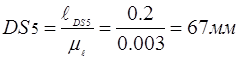
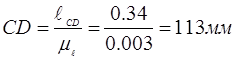 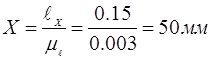
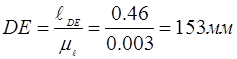 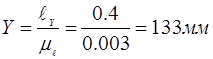
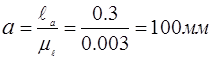 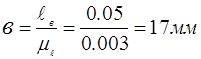
Сначала определили крайнее положение механизма перед рабочим ходом и начиная от него построили 6–8 планов положений механизма соответствующих положениям ведущего звена механизма. Определили 2-ое крайнее положение звеньев механизма и построили для него план механизма. Построили диаграмму усилий, действующее на исполнительное звено, и если необходимо, построили 2 плана положений соответствующие началу и концу действия сил полезного сопротивления.
Структурный анализ механизма
1. Выписываем кинематические пары определяя класс и вид
1–2 – вращ., 5 кл
2–3 – вращ., 5 кл
3–4 – поступ., 5 кл
4–1 – вращ., 5 кл
4–5 – вращ., 5 кл
5–6 – вращ., 5 кл
6–1 – поступ., 5 кл

2. Определяем степень подвижности
W=3n-2p5
– p4
=3*5–2*7=1
3. Строим структурную схему механизма
4. Определяем группы Ассура, определяем класс, порядок и вид
5–6 гр. Ассура, II класса, II порядка, с внешней поступательной парой
Реклама

3–4 гр. Ассура, II класса, II порядка, с внутренней поступательной парой
1–2 механизм I класса
5. Определяем точки наслоения
I(1,2) – II(3,4) – III(5,6)
Весь механизм II класса.
Планы скоростей. Линейные скорости точек и угловые скорости звеньев
Построение плана скоростей
Скорость точки A
постоянна и равна:
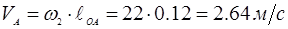
Выбираем масштаб плана скоростей. Пусть отрезок 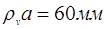 - изобр. скорость т.А на плане скоростей. Тогда масштаб плана скоростей будет: - изобр. скорость т.А на плане скоростей. Тогда масштаб плана скоростей будет:
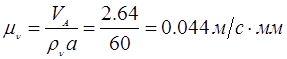
Вектор pv
а направлен перпендикулярно ОА
по направлению ω2.
Рассмотрим группу Ассура 3–4 (внутренняя точка А4
) и запишем систему уравнений:
VA
4
=
VA
+
VA
4А
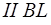
VA
4
=
V
С
+
VA
4С
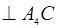
Систему решим графически. Рассмотрим первое уравнение системы: через точку a
плана скоростей проводим прямую, параллельную звену BL
(на этой прямой будет находиться VA
4А
и точка A
4
).
Решаем второе уравнение.V
С
=0
, т. к. точка С
неподвижна, а значит вектор pv
с
, изображающий скорость V
С
=0
иточка С совпадает с pv
.
Через полюс плана скоростей (точки с)
проводим прямую перпендикулярную А4
C
. При пересечении двух прямых получаем положение точки а4
.
Положение точек b
,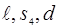 на плане скоростей определяем по теоремам подобия. Точка b
будет находиться так: на плане скоростей определяем по теоремам подобия. Точка b
будет находиться так:
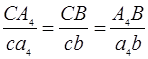
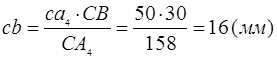
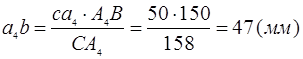
Проведём окружность радиусом а4
b
с центром в точке а4
и радиусом cb
с центром в точке c
, пересечение их является точка b
. Из полюса pv
проводим вектор в точку b
.
Точка 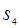 , , 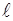 будет находиться на отрезке b
а4
, причём: будет находиться на отрезке b
а4
, причём:
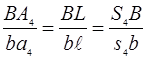
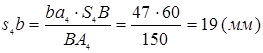
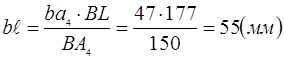
Точка d
будет находиться на отрезке bc
, причём:
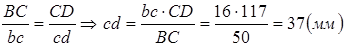
Рассмотрим группу Ассура 5–6
(внутренняя точка Е
) и запишем систему уравнений:
V
Е
= VD
+ VED
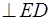
VE
= VP
+ VEP
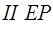
Систему решим графически. Рассмотрим первое уравнение системы: через точку d
плана скоростей проводим прямую 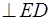 (на этой прямой будет находиться VED
и точка E
). (на этой прямой будет находиться VED
и точка E
).
Решаем второе уравнение.VP
=0
, т. к. точка P
неподвижна, а значит вектор pv
p
, изображающий скорость VP
=0
иточка P
совпадает с pv
.
Через полюс плана скоростей (точки p
)
проводим прямую 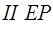 . При пересечении двух прямых получаем положение точки e
(
s
6
)
.
. При пересечении двух прямых получаем положение точки e
(
s
6
)
.
Точка 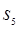 будет находиться на отрезке de
(
ds
6
),
причём: будет находиться на отрезке de
(
ds
6
),
причём:
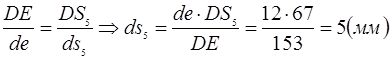
Определим истинные значения линейных скоростей точек и угловых скоростей звеньев механизма:
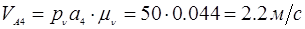
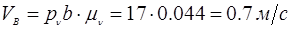
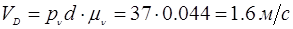
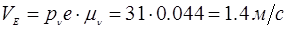
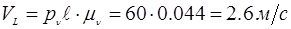
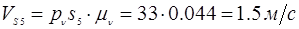
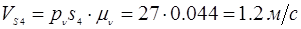
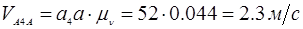
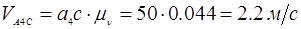
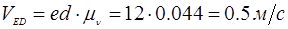
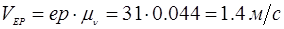
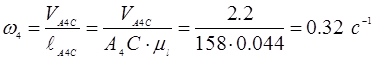 

План скоростей рассмотрен для выделенного положения.
Аналогично строится планы скоростей для остальных положений механизма.
Реклама

Результаты заносятся в таблицу скоростей точек и звеньев механизма.
Таблица 1 – Линейные скорости характерных точек и угловые скорости звеньев
| Параметр |
Значение в положении |
| 1 |
2 |
Основное |
4 |
5 |
6 |
7 |
8 |
9 |
| VА4, м/с
|
0 |
1.32 |
2.2 |
2.7 |
0.6 |
1.5 |
0 |
1.3 |
2.5 |
| VB,
м/с
|
0 |
0.5 |
0.7 |
0.8 |
0.6 |
0.4 |
0 |
0.6 |
1.1 |
| VD
, м/с
|
0 |
1.1 |
1.6 |
1.9 |
1.3 |
1. |
0 |
1.1 |
2.7 |
| VE
, м/с
|
0 |
0.8 |
1.4 |
2 |
1.4 |
1.1 |
0 |
1.2 |
2.6 |
| VS4
, м/с
|
0 |
0.7 |
1.2 |
1.2 |
0.9 |
0.7 |
0 |
0.7 |
1.8 |
| VS5
, м/с
|
0 |
1 |
1.5 |
0.2 |
1.4 |
1.1 |
0 |
1.1 |
2.6 |
| VL
,м/с
|
0 |
1.7 |
2.6 |
2.9 |
2.1 |
1.7 |
0 |
1.8 |
4.1 |
| VA4A
,м/с
|
0 |
2.8 |
2.3 |
0.4 |
1.4 |
1.8 |
0 |
2.8 |
1.2 |
| VA4C
,м/с
|
0 |
1.3 |
2.2 |
2.7 |
0.6 |
1.5 |
0 |
1.3 |
2.5 |
| VED
,м/с
|
0 |
0.4 |
0.5 |
0.4 |
0.3 |
0.3 |
0 |
0.3 |
0.2 |
| VEP
,м/с
|
0 |
0.8 |
1.4 |
2 |
1.4 |
1.1 |
0 |
1.2 |
2.6 |
| ω4
,
с-1
|
0 |
0.2 |
0.3 |
0.4 |
0.1 |
0.2 |
0 |
0.2 |
0.5 |
| ω5
,
с-1
|
0 |
1 |
1.1 |
0.8 |
0.7 |
0.6 |
0 |
0.6 |
0.4 |
5. Построение диаграммы приведенного момента сил сопротивления
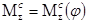
Определение точки приложения и направление уравновешивающей силы (приведенной силы)
Для определения полюса зацепления 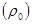 в зубчатой передаче, принять радиус делительной окружности ведомого колеса 2 в зубчатой передаче, принять радиус делительной окружности ведомого колеса 2 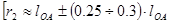  . .
Выделить более четкими линиями один из планов механизма на рабочем ходу (где действует сила полезного сопротивления), но не крайние положения. Для этого положения пронумеровать звенья и обозначить кинематические пары и центры масс звеньев. Нумерацию планов положений начать с крайнего положения перед рабочим ходом.
Определяем радиус делительной окружности ведомого колеса
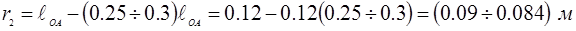
Принимаем r
2
=0,09 м
, используя масштаб 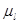 , определим масштаб на плане механизма: , определим масштаб на плане механизма:
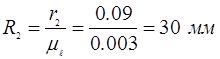
На плане механизма находится точка полюса зацепления (т. р0
), а также направ-ление уравновешивающей силы (приведенной силы и ее точки приложения т. В2
)
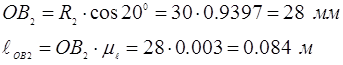
Используя теорему подобия находим положения и скорость т. В2
на планах скоростей в каждом положении:
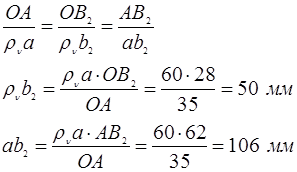
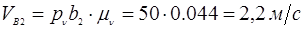
Пара-
метры
|
Положения |
| 1 |
2 |
Основное |
4 |
5 |
6 |
7 |
8 |
9 |
| pv
b
2
мм |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
50 |
| ab2
мм |
105 |
110 |
106 |
82 |
46 |
38 |
17 |
22 |
55 |
| VB2
м/с |
2.2 |
2.2 |
2.2 |
2.2 |
2.2 |
2.2 |
2.2 |
2.2 |
2.2 |
Определение силы полезного сопротивления по диаграмме сил и силы тяжести звеньев в каждом положении и прикладывание его к механизму
Определяем силы тяжести:
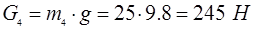
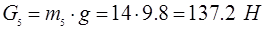 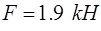
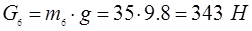
Значение сил полезного сопротивления и сил тяжести звеньев во всех положениях механизма одинаковы, кроме 1-ого и 7-ого, где F
=0
Силы проставляются только в выделенном положении.
Согласно теоремы Жуковского «О жестком рычаге», перенести все силы из плана механизма на план скоростей повернув их на 900
в том числе 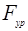 . .
Взять сумму моментов всех сил относительно pv
и найти величину, направление 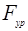 . .
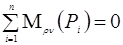
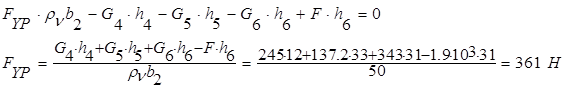
Уравновешивающий момент:
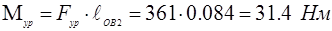
Поскольку приведенная сила сопротивления 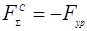 и приведенный момент сопротивления и приведенный момент сопротивления 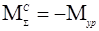 то имеем значения приведенных моментов сил сопротивления. Каждый момент заносим в таблицу то имеем значения приведенных моментов сил сопротивления. Каждый момент заносим в таблицу
Таблица 3 – Приведенные значения моментов сил полезного сопротивления
| Положения |
1 |
2 |
Основное |
4 |
5 |
6 |
7 |
8 |
9 |
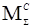 , кНм
, кНм
|
0 |
19,5 |
31,4 |
46 |
33 |
25,9 |
0 |
15,9 |
10 |
По значениям 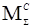 в таблице строим график в таблице строим график 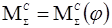 на миллиметровке. на миллиметровке.
Определение мощности электродвигателя и разбивка передаточного отношения по ступеням. Определив 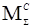 для каждого положения строим график изменения приведенного момента сил сопротивления от функции угла поворота звена приведения по оси абсцисс, масштаб равен: для каждого положения строим график изменения приведенного момента сил сопротивления от функции угла поворота звена приведения по оси абсцисс, масштаб равен:
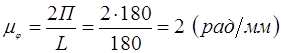
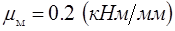
Имея зависимость 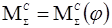 определяем требуемую мощность электродвигателя, для этого находим работу сил сопротивления: определяем требуемую мощность электродвигателя, для этого находим работу сил сопротивления:
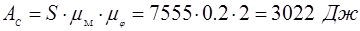 , ,
где S – площадь, мм2
Тогда работа движущих сил:
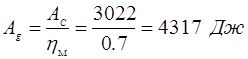 , ,
где Ag
– полезная работа механизма, 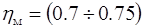
Средняя мощность движущих сил:
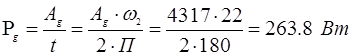
Требуемая мощность электродвигателя: 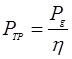 , ,
где 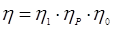
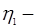 КПД зубчатой передачи, КПД зубчатой передачи, 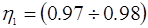 - цилиндрическая передача - цилиндрическая передача
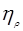 - КПД ременной передачи, - КПД ременной передачи, 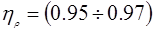
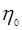 - КПД одной пары подшипников качения, - КПД одной пары подшипников качения, 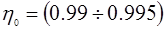
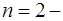 количество пар подшипников качения количество пар подшипников качения
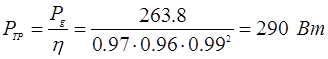
По ГОСТ 19523–81 выбираем 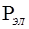 , причем , причем 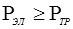 , согласно , согласно 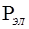 выбираем синхронную частоту вращения выбираем синхронную частоту вращения 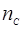 , процент скольжения S
. Соответственно выбрали: , процент скольжения S
. Соответственно выбрали:
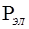 =0,55 кВт,
=0,55 кВт, 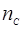 =1500 об/мин,
S
=7,3% =1500 об/мин,
S
=7,3%
Определяем номинальное число оборотов электродвигателя:
 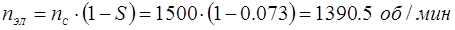
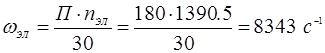
Определяем передаточное число, общее:
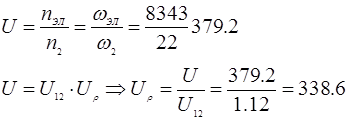
где 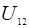 - передаточное число редуктора, выбираем по ГОСТ 2185–66 - передаточное число редуктора, выбираем по ГОСТ 2185–66
Up
– передаточное число ременной передачи
 радиус делительной окружности шестерни радиус делительной окружности шестерни
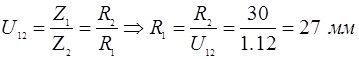
Построение диаграммы изменения кинетической энергии
Имея диаграмму  сил сопротивления сил сопротивления 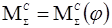 графически проинтегрируем ее методом хорд и получим график работы сил сопротивления графически проинтегрируем ее методом хорд и получим график работы сил сопротивления 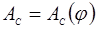 . Масштаб графика получим вычисляя по формуле: . Масштаб графика получим вычисляя по формуле:
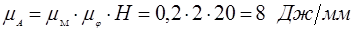 , ,
где 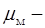 масштаб масштаб 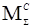
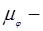 масштаб оси масштаб оси 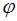
Н –
полюсное расстояние при графическом интегрировании, мм
Приведенный момент движения сил для промышленных установок принимаем постоянным в течение всего цикла установившегося режима. Учитывая то обстоятельство, что за полный цикл установившегося движения работа движущих сил равна работе сил сопротивления. Соединяем 1-ую и последнюю точки в диаграмме 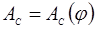 прямой линией. Указанная прямая в положительной области представляет собой диаграмму работ движущих сил прямой линией. Указанная прямая в положительной области представляет собой диаграмму работ движущих сил 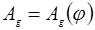 . Вычитая из ординат диаграммы . Вычитая из ординат диаграммы 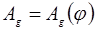 соответствующие ординаты диаграммы соответствующие ординаты диаграммы 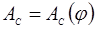 и откладывая разность на соответствующей ординате получаем диаграмму изменения (приращения) кинетической энергии механизма и откладывая разность на соответствующей ординате получаем диаграмму изменения (приращения) кинетической энергии механизма 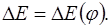
Определение истинной скорости движения звена приведения
Построение диаграммы приведенного момента инерции по уровню:
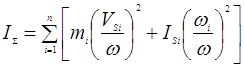
Определяем значения приведенного момента инерции в каждом положении:
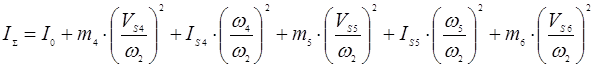
Результат заносим в таблицу.
Таблица 4 – Значения приведенных моментов инерции
| Положение |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
 |
0,15 |
0,25 |
0,43 |
0,52 |
0,39 |
0,3 |
0,15 |
0,32 |
0,86 |
По полученным значениям строим график изменения приведенного момента инерции от функции угла поворота звена приведения  . .
Масштаб 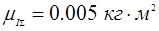
Построение диаграммы «Энергия – масса» (кривой Виттенбауэра) и зависимости
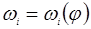
Исключив из графиков 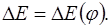 и и 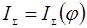 аргумент φ
получим функциональную зависимость изменения приращения к кинетической энергии от приведенного момента инерции аргумент φ
получим функциональную зависимость изменения приращения к кинетической энергии от приведенного момента инерции 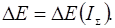 - диаграмму Виттенбауэра. - диаграмму Виттенбауэра.
Кинетическая энергия механизма в любой момент времени можно представить в виде суммы кинетической энергии механизма в начальный момент времени 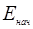 и разности работ сил движущих Ag
и сил сопротивления Aс
за время соответствующее повороту звена приведения на угол φ,
т.е. и разности работ сил движущих Ag
и сил сопротивления Aс
за время соответствующее повороту звена приведения на угол φ,
т.е.

Переносим начало координат графика 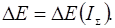 на расстояние соответствующее значению кинетической энергии на расстояние соответствующее значению кинетической энергии 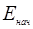 . .
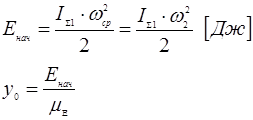
В этом случае диаграмма Виттенбауэра отнесенная к новой системе координат, представляет кривую изменения кинетической энергии всего механизма функции приведенного момента инерции 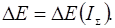
Истинная скорость звена приведения в данном его положении:
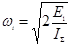 (1) (1)
Взяв на кривой 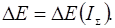 произвольно выбрав точку с координатами (х, у)
и определив значение: произвольно выбрав точку с координатами (х, у)
и определив значение:
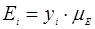 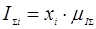
После подстановки в формулу (1) получим:
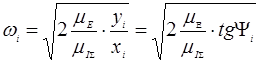 (2) (2)
Полученные данные 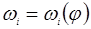 заносим в таблицу. заносим в таблицу.
Таблица 5-Значения истинной скорости движения звена приведения
| Положение |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
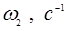 |
По значениям таблицы строим диаграмму изменения истинной скорости движения звена приведения 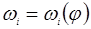 . .
Из нового начала координат т. О1
касательно к диаграмме 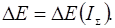 проводим проводим
Лучи и находим лучи 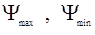 , тогда по формуле (2) находим , тогда по формуле (2) находим 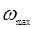 , ,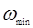 . Угловые . Угловые
Скорости звена приведения:
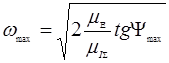  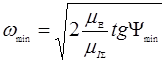
|