Министерство образования и науки Украины
Севастопольский национальный технический университет
«ПОКАЗАТЕЛИ ВАРИАЦИИ»
«ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ»
«РЯДЫ ДИНАМИКИ»
Методические указания и задания по дисциплине «Статистика. Часть 1» для студентов экономических специальностей всех форм обучения
Севастополь
2008
УДК 311(075.8)
«Показатели вариации», «Выборочное наблюдение», «Ряды динамики» Методические указания и задания по дисциплине «Статистика. Часть 1» для студентов экономических специальностей всех форм обучения/ Сост. Т.Н. Кашо, И.В. Березина. — 1- е изд. —Севастополь: Изд-во СевНТУ, 2008. — 40c.
Целью методических указаний является оказание помощи студентам в изучении методов статистических расчетов путем обеспечения материалами для закрепления теоретических знаний и получения навыков решения практических заданий. Излагаются основные понятия, формулы, примеры и решения типовых задач, контрольные вопросы и тесты по изучаемым темам и библиографический список. Указания предназначены для студентов экономических специальностей всех форм обучения.
Методические указания рассмотрены и утверждены на заседании кафедры «Учет и аудит» СевНТУ (протокол № 11 от 27 июня 2007 г.).
Допущено учебно-методическим центром СевНТУ в качестве методических указаний.
Рецензенты:
О.В. Луняков, канд. экон. наук, доцент кафедры «Менеджмент организаций» СевНТУ
О.С. Доценко, ст. преп. кафедры «Учет и аудит» СевНТУ
СОДЕРЖАНИЕ
Введение................................................................................................……… 4
1. Показатели вариации...............................................................…........….. 5
1.1. Основные формулы............................................................................. 5
1.2. Решение типовых задач...................................................................... 7
1.3. Контрольные задачи............................................................................ 10
1.4. Контрольные вопросы........................................................................ 12
1.5. Тесты..................................................................................................... 13
2. Выборочное наблюдение.......................................................................... 16
Реклама

2.1. Основные формулы............................................................................. 16
2.2. Решение типовых задач...................................................................... 18
2.3. Контрольные задачи............................................................................ 20
2.4. Контрольные вопросы........................................................................ 22
2.5. Тесты..................................................................................................... 22
3. Ряды динамики.......................................................................................... 25
3.1. Основные формулы............................................................................. 25
3.2. Решение типовых задач...................................................................... 28
3.3. Контрольные задачи............................................................................ 31
3.4. Контрольные вопросы........................................................................ 34
3.5. Тесты..................................................................................................... 34
Вопросы для подготовки к зачету по дисциплине «Статистика.Часть1» …37
Библиографический список.......................................................................... 38
ВВЕДЕНИЕ
Настоящее методико-учебное пособие содержит задачи курса «Статистика. Часть 1» с целью сориентировать студентов на подготовку по темам: «Показатели вариации», «Выборочное наблюдение», «Ряды динамики». С этой же целью в конце пособия приведен библиографический список по всему курсу и перечень вопросов к зачету.
Готовясь к практическим занятиям, студент должен прочесть рекомендованную литературу и конспект лекций, самостоятельно проверить, как он усвоил вопросы той темы, по которой будет решать задачи.
Решение задач необходимо сопровождать соответствующими формулами, подробными расчетами, пояснением сущности исследуемых показателей и краткими выводами. При этом особое внимание следует уделять экономическому содержанию показателей.
Расчеты должны быть выполнены с принятой в статистике точностью: индексы рассчитываются с точностью до 0.001, а проценты - до 0.01. При выполнении работ рекомендуется использовать статистические таблицы, которые должны быть построены и оформлены по правилам, изучающимся в теме «Сводка и группировка статистических данных».
Реклама

В соответствии с учебной программой студентам всех форм обучения необходимо иметь навык в решении определенных задач, согласно требованиям и выполнить по данному разделу домашнюю контрольную работу. По окончании курса предусмотрен зачет.
Данные методические указания значительно упростят процесс изучения материала, т.к. в нем систематизированы темы раздела, основные формулы по темам, которыми необходимо пользоваться. Для повышения эффективности самостоятельной работы приведены подробные выкладки всех расчетных формул с ответами по каждой типовой задаче, а так же представлены примеры решения распространенных задач для самостоятельного решения. В конце каждой темы приведены контрольные вопросы и тесты, ответы на которые обеспечат положительный результат при сдаче зачета.
Перед выполнением контрольной работы или решением задач на практических занятиях требуется внимательное изучение настоящих методических указаний.
1. ПОКАЗАТЕЛИ ВАРИАЦИИ
Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Различают вариацию случайную и систематическую. К показателям вариации относят: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение – являются абсолютным измерением вариации и коэффициент вариации – относительный показатель вариации.
1.1. Основные формулы
Размах вариации (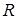 ): ):
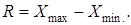 |
(1.1) |
Среднее линейное отклонение (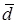 ): ):
а) для несгруппированных данных:
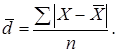 |
(1.2) |
б) для сгруппированных данных:
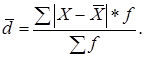 |
(1.3) |
Дисперсия (s2
):
а) простая дисперсия для несгруппированных данных:
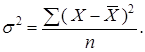 |
(1.4) |
б) взвешенная дисперсия для вариационного ряда:
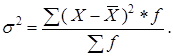 |
(1.5) |
Упрощенные методы расчета дисперсии:
1. Метод электронно-вычислительного способа расчета :
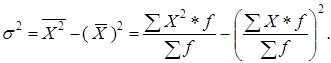 |
(1.6) |
2. По «способу моментов»:
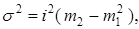 |
(1.7) |
где m2
– момент второго порядка, определяемый по формуле:
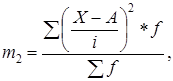 |
(1.8) |
где m1
– момент первого порядка, определяемый по формуле (4.10).
Дисперсия альтернативного признака (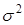 ): ):
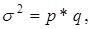 |
(1.9) |
где p – доля единиц, обладающих альтернативным признаком;
q – доля единиц, не обладающих альтернативным признаком(q = 1 - p).
Среднее квадратическое отклонение (s ):
 |
(1.10) |
Правило сложения дисперсий:
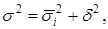 |
(1.11) |
где s2
– общая дисперсия;
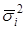 - средняя из внутригрупповых дисперсий; - средняя из внутригрупповых дисперсий;
d2
– дисперсия групповых средних (межгрупповая) дисперсия.
Средняя из внутригрупповых дисперсий:
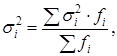 |
(1.12) |
где 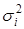 - групповые дисперсии. - групповые дисперсии.
Внутригрупповые дисперсии:
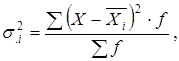 |
(1.13) |
где 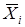 - групповые средние; - групповые средние;
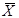 - общая средняя. - общая средняя.
Межгрупповая дисперсия:
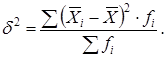 |
(1.14) |
Коэффициент вариации (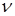 ): ):
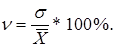 |
(1.15) |
Коэффициент детерминации ( 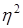 ): ):
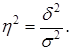 |
(1.16) |
Эмпирическое корреляционное отношение (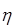 ): ):
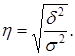 |
(1.17) |
1.2. Решение типовых задач
Задача № 1.1
Имеются данные о сменной выработке рабочих бригады, представленные интервальным рядом распределения (исходные данные в столбцах 1-2):
| Группы рабочих по сменной выработке, шт. |
Число рабочих, чел.
(
f
)
|
Расчетные значения |
Середина интервала
(
X)
|
X*f
|

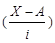
|
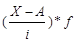
|
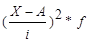
|
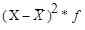
|
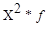
|
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 170-190 |
10 |
180 |
1800 |
-2 |
-20 |
40 |
12960 |
324000 |
| 190-210 |
20 |
200 |
4000 |
-1 |
-20 |
20 |
5120 |
800000 |
| 210-230 |
50 |
220 |
11000 |
0 |
0 |
0 |
800 |
2420000 |
| 230-250 |
20 |
240 |
4800 |
1 |
20 |
20 |
11520 |
1152000 |
| Итого |
100 |
- |
21600 |
- |
-20 |
80 |
30400 |
4696000 |
Определить:
а) среднесменную выработку рабочих;
б) дисперсию выработки;
в) среднее квадратическое отклонение;
г) коэффициент вариации.
Сделать вывод.
Решение:
а) среднесменная выработка рабочих определяется:
– по формуле средней арифметической взвешенной:
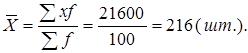
– по «способу моментов»:
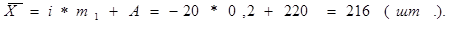
где А – середина интервала, обладающего наибольшей частотой: f маx =50, А=220.
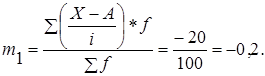
б) дисперсия выработки рассчитывается:
– по формуле средневзвешенной дисперсии:
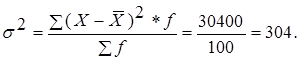
– по упрощенным методам расчета дисперсии:
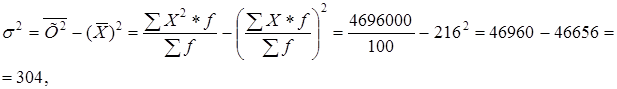
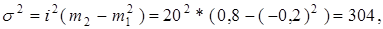
где 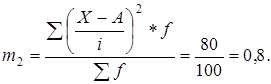
в) среднее квадратическое отклонение рассчитывается по формуле:
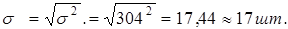
г) коэффициент вариации определяется по формуле:
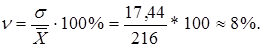
Вывод: данная бригада достаточно однородна по выработке и средняя считается надежной и типичной, поскольку вариация признака составляет лишь 8%, т. е. больше 33%.
Задача № 1.2
При изучении влияния квалификации рабочих на уровень производительности труда в цехе были получены данные, представленные в следующей таблице (исходные данные в столбцах 1, 2, 4, 5):
Номер
расчетных
значений
|
Рабочие 4-го разряда |
Номер
расчетных
значений
|
Рабочие 5-го разряда |
Выработка
рабочего,
шт.
|
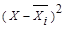 |
Выработка
рабочего,
шт.
|
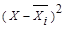 |
| 1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
7 |
9 |
1 |
14 |
1 |
| 3 |
9 |
1 |
3 |
15 |
0 |
| 4 |
10 |
0 |
4 |
17 |
4 |
| 5 |
12 |
4 |
| 6 |
13 |
9 |
| Итого |
60 |
24 |
Итого |
60 |
6 |
Определить:
а) внутригрупповые дисперсии;
б) среднюю из внутригрупповых дисперсий;
в) межгрупповую дисперсию;
г) общую дисперсию;
д) проверить правило сложения дисперсий.
Решение:
В этом примере данные группируются по квалификации рабочих, являющихся факторным признаком. Результативный признак варьирует как под влиянием систематического фактора – квалификации (межгрупповая вариации), так и других неучтенных случайных факторов (внутригрупповая вариация). Задача заключается в измерении этих вариаций с помощью дисперсий: общей, межгрупповой и внутригрупповых.
а) средняя выработка по каждой бригаде считается по формулам арифметической простой и взвешенной:
- по первой группе: 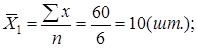
- по второй группе: 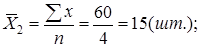
- по двум группам: 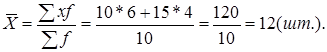
Внутригрупповые дисперсии показывают вариацию выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме различий в квалификационном разряде (внутри группы все рабочие имеют одну квалификацию) и рассчитываются по формуле:
- по первой группе: 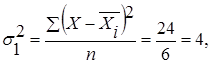 где где 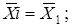
- по второй группе: 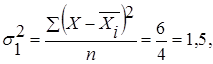 где где 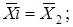
б) средняя из внутригрупповых дисперсий отражает вариацию выработки, обусловленную всеми факторами, кроме квалификации рабочих, но в среднем по всей совокупности и рассчитывается по формуле:
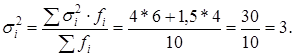
в) межгрупповая дисперсия характеризует вариацию групповых средних, обусловленную различиями групп рабочих по квалификационному разряду и рассчитывается по формуле:
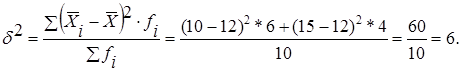
г) общая дисперсия отражает суммарное влияние всех возможных факторов на общую вариацию средних, обусловленную различиями групп рабочих по квалификационному разряду и рассчитывается по формуле:
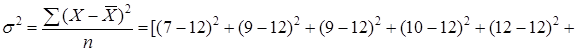 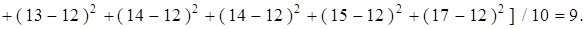
д) правило сложения дисперсий:
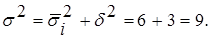
1.3. Контрольные задачи
Задача № 1.1
Имеются данные о распределении заводов по стоимости готовой продукции в следующей таблице:
| Номер группы |
Группы заводов
по стоимости готовой продукции,
млн. у.е.
|
Число заводов |
| 1 |
до 2 |
10 |
| 2 |
2 – 3 |
20 |
| 3 |
3 – 4 |
30 |
| 4 |
4 – 5 |
25 |
| 5 |
5 – 6 |
10 |
| 6 |
свыше 6 |
5 |
На основании приведенных данных вычислить:
а) среднюю стоимость продукции на один завод;
б) дисперсию и среднее квадратическое отклонение;
в) коэффициент вариации и сделать выводы.
Задача № 1.2
В целях изучения норм выработки рабочих на заводе было обследовано 400 рабочих, показавших затраты времени на обработку одной детали. Данные представлены в следующей таблице:
Затраты времени на одну деталь,
мин.
|
Число рабочих,
чел.
|
| до 14 |
40 |
| 14 –16 |
100 |
| 16 – 18 |
150 |
| 18 – 20 |
70 |
| свыше 20 |
40 |
| Итого |
400 |
Вычислить:
а) средние затраты времени на обработку одной детали;
б) дисперсию по формуле 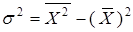 ; ;
в) коэффициент вариации.
Задача № 1.3
В целях изучения возрастной структуры рабочих завода по состоянию на 1 июля было проведено обследование, результаты которого показали распределение рабочих по возрасту, представленное в следующей таблице:
Группы рабочих по возрасту,
лет
|
Число рабочих,
чел.
|
| до 20 |
5 |
| 20 – 25 |
10 |
| 25 – 30 |
14 |
| 30 – 35 |
20 |
| 35 – 40 |
22 |
| 40 – 45 |
19 |
| свыше 45 |
10 |
| Итого |
100 |
Вычислить:
а) средний возраст рабочего;
б) среднее квадратическое отклонение;
в) Коэффициент вариации.
Задача № 1.4
Имеются данные о распределении изделий А по весу в следующей таблице:
Вес изделий,
г.
|
Число изделий,
шт.
|
| до 200 |
4 |
| 200 – 205 |
10 |
| 205 – 210 |
60 |
| 210 – 215 |
20 |
| свыше |
6 |
Вычислить:
1. По «способу моментов»:
а) средний вес изделия;
б) дисперсию и среднее квадратическое отклонение.
2. Коэффициент вариации. Сделать выводы.
Задача № 1.5
Было опрошено студентов о времени, затрачиваемом ими на дорогу в институт. Результаты обследования представлены в следующей таблице:
Время,
затрачиваемое студентом на дорогу, мин.
|
Число студентов,
чел.
|
| до 15 |
2 |
| 15 – 30 |
18 |
| 30 – 45 |
45 |
| 45 – 60 |
25 |
| свыше 60 |
10 |
| Итого |
100 |
На основании выборочных данных вычислить:
1. По «способу моментов»:
а) среднее время, затрачиваемое на дорогу в институт;
б) среднее квадратическое отклонение.
2. Коэффициент вариации.
Задача № 1.6
Определить групповые дисперсии, среднюю из групповых дисперсий, межгрупповую и общую дисперсии по данным, приведенным в следующей таблице:
| Первая бригада |
Вторая бригада |
Номер
рабочих
|
Изготовлено
деталей за час,
шт.
|
Номер
рабочих
|
Изготовлено
деталей за час,
шт.
|
| 1 |
13 |
7 |
18 |
| 2 |
14 |
8 |
19 |
| 3 |
15 |
9 |
22 |
| 4 |
17 |
10 |
20 |
| 5 |
16 |
11 |
24 |
| 6 |
15 |
12 |
23 |
| Итого |
90 |
Итого |
126 |
1.4. Контрольные вопросы
1. Необходимость измерения вариации признаков, от чего зависит ее размер.
2. Среднее линейное отклонение, размах вариаций и их недостатки как показателей вариации.
3. Среднее квадратическое отклонение, дисперсия и особенности расчета для несгруппированных и вариационных рядов распределения.
4. Цель расчет коэффициента вариации.
5. Основные свойства дисперсии.
6. Сущность упрощенного расчета дисперсии.
7. Дисперсия альтернативного признака.
8. Группы факторов, вызывающих вариацию признака.
9. Методы расчета общей, групповой и межгрупповой дисперсий. Правило сложения дисперсий, его практическое значение.
10. Смысл расчет эмпирического коэффициента детерминации и корреляционного отношения.
11. Характеристика форм распределения.
1.5. Тесты
1. Вариация – это:
а) качественные изменения признака в пределах однородной совокупности, обусловленные влиянием различных факторов;
б) различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени;
в) изменение («колеблемость») величины либо значения признак при переходе от одной единицы совокупности к другой;
г) все ответы верны.
2. К абсолютным показателям вариации относят:
а) размах вариации;
б) коэффициент вариации;
в) мода;
г) среднее квадратическое отклонение;
д) дисперсия.
3. К относительным показателям вариации относят:
а) коэффициент интенсивности;
б) коэффициент вариации;
в) среднее линейное отклонение;
г) среднее квадратическое отклонение;
д) дисперсия.
4. Размах вариации представляет собой:
а) разность между максимальным и минимальным значениями признака;
б) разность между минимальным и максимальным значениями признака;
в) сумма минимального и максимального значения признака;
г) свой ответ.
5. Формула для расчета простой дисперсии для несгруппированных данных имеет вид ______.
6. Формула для расчета дисперсии для вариационного ряда имеет вид ________.
7. Корень квадратный из дисперсии – это:
а) среднее линейное отклонение;
б) среднее квадратическое отклонение;
в) размах вариации;
г) свой ответ.
8. Чем _______ значения дисперсии и среднего квадратического отклонения, тем однороднее совокупность и тем более _____ будет средняя величина.
9. Коэффициент вариации применяют:
а) для сравнения вариаций различных признаков;
б) для характеристики однородности совокупности;
в) для сравнения колеблемости одного и то же признака в нескольких неоднородных совокупностях;
г) все ответы верны.
10. Коэффициент вариации представляет собой:
а) выраженное абсолютным показателем отношение среднего квадратического отклонения к средней арифметической;
б) отношение среднего линейного отклонения к средней арифметической;
в) выраженное в % отношение среднего квадратического отклонения к средней арифметической;
г) свой ответ.
11. Совокупность считается количественно однородной, а средняя типичной, если коэффициент вариации
а) равен 33%;
б) больше 44%;
в) больше 33%;
г) не превышает 33%.
12. Если все значение признака увеличить или уменьшить на одну и ту же постоянную величину А, то дисперсия от этого:
а) увеличится или уменьшиться на величину А;
б) предсказать нельзя;
в) не изменится;
г) нет верного ответа.
13. Распределение рабочих по заработной плате показано в следующей таблице:
Группы рабочих
по заработной плате, у.е.
|
500 – 600 |
600 – 700 |
700 – 800 |
800 – 900 |
Итого |
| Число рабочих, чел |
6 |
10 |
8 |
6 |
30 |
Определить дисперсию по «способу моментов»:
а) 10018;
б) 5005;
в) 10491;
г) 2890.
14. Выделяют следующие виды дисперсий:
а) общая;
б) межгрупповая;
в) хронологическая;
г) линейная;
д) внутригрупповая
15. Общая дисперсия измеряет ______________.
16. Отражает случайную вариацию:
а) общая дисперсия;
б) межгрупповая дисперсия;
в) внутригрупповая дисперсия;
г) средняя из внутригрупповых дисперсий.
17. Систематическую вариацию результативного признака характеризует:
а) общая дисперсия;
б) межгрупповая дисперсия;
в) внутригрупповая дисперсия;
г) средняя из внутригрупповых дисперсий.
18. Распределение рабочих по сменной выработке изделия А показано в следующей таблице:
| Группы рабочих по сменной выработке, шт. |
до 100 |
100 – 150 |
150 – 200 |
200 – 250 |
Итого |
| Число рабочих, чел |
10 |
20 |
50 |
20 |
100 |
Определить дисперсию по формуле для сгруппированных данных:
а) 1900;
б) 1700;
в) 1600;
г) свой ответ.
19. Согласно правилу сложения дисперсий общая дисперсия равна:
а) сумме средней из внутригрупповых и межгрупповой дисперсий;
б) сумме внутригрупповых и межгрупповой дисперсий;
в) сумме внутригрупповых дисперсий;
г) свой ответ.
20. Долю вариации результативного признака Y под влиянием факторного признака Xпоказывает:
а) эмпирическое корреляционное отношение;
б) эмпирический коэффициент детерминации;
в) средняя из внутригрупповых дисперсий;
г) коэффициент структуры.
21. Тесноту связи между группировочным и результативным признаками показывает:
а) эмпирическое корреляционное отношение;
б) эмпирический коэффициент детерминации;
в) средняя из внутригрупповых дисперсий;
г) коэффициент структуры;
22. Однородные совокупности характеризуются ___________ распределением:
а) одновершинным;
б) многовершинным;
в) двухвершинным;
г) свой ответ.
23. Для симметричного распределения имеет место следующее соотношение:
а) Х равно Мо равно Ме;
б) Х больше Мо больше Ме;
в) Х меньше Мо меньше Ме;
г) нет верного ответа.
24. Крутость вариационного ряда называют:
а) ассиметрией;
б) симметрией;
в) эксцессом;
г) свой ответ
25. Отрицательный знак показателя ассиметрии свидетельствует о:
а) правосторонней ассиметрии;
б) левосторонней ассиметрии;
в) несущественности показателя ассиметрии;
г) существенности показателя ассиметрии.
26. Особенности кривой нормального распределения:
а) симметрична относительно центра распределения;
б) эксцесс больше 0, ассиметрия больше 0;
в) эксцесс равен 0, ассиметрия равна 0;
г) в промежутке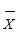 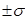 находится 60% всех значений признака; находится 60% всех значений признака; 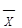 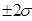 - 70% всех значений признака; - 70% всех значений признака; 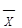 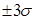 - 90% всех значений признака; - 90% всех значений признака;
д) в промежутке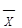 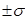 находится 68,3% всех значений признака; находится 68,3% всех значений признака; 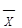 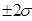 - 95,4% всех значений признака; - 95,4% всех значений признака; 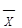 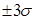 - 99,7% всех значений признака. - 99,7% всех значений признака.
2. ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
Выборочное наблюдение – это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность. Наблюдение организуется таким образом, что эта часть отобранных единиц в уменьшенном масштабе репрезентирует (представляет) всю совокупность.
Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.
2.1. Основные формулы
Средняя ошибка выборки при собственно случайном методе отбора (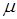 ): ):
а) повторный отбор:
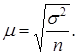 |
(2.1) |
б) бесповторный отбор:
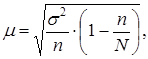 |
(2.2) |
где n – численность выборочной совокупности;
N – численность генеральной совокупности;
s2
– дисперсия средней или доли;
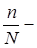 процент выборки. процент выборки.
Дисперсия средней 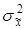 находится с использованием формул, указанных в п. 5. находится с использованием формул, указанных в п. 5.
Дисперсия выборочной доли:
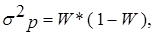 |
(2.3) |
где 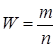 - доля единиц, обладающих данным признаком в выборочной совокупности; - доля единиц, обладающих данным признаком в выборочной совокупности;
m – единицы выборочной совокупности, обладающие данным признаком.
Предельная ошибка выборки ( D ):
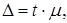 |
(2.4) |
где t – коэффициент кратности (доверия).
Доверительные интервалы:
| а) для средней: |
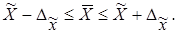 |
(2.5) |
| б) для доли: |
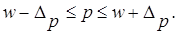 |
(2.6) |
Объем выборки при повторном отборе:
| а) для средней |
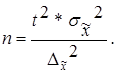 |
(2.7) |
| б) для доли: |
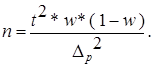 |
(2.8) |
Объем выборки при бесповторном отборе:
| а) для средней |
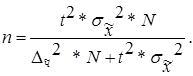 |
(2.9) |
| б) для доли: |
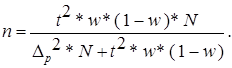 |
(2.10) |
2.2. Решение типовых задач
Задача № 2.1
В целях изучения затрат времени на изготовление детали рабочими завода проведена 10% случайная бесповторная выборка в результате которой получено данное распределение деталей по затратам времени, представлено в следующей таблице:
Затраты
времени
на одну деталь, мин.
|
Число
деталей,
шт.
|
Расчетные значения |
| Середина интервала (X) |
 |
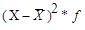 |
| до 10 |
10 |
9 |
90 |
136,9 |
| до 12 |
20 |
11 |
220 |
57,8 |
| 12 – 14 |
50 |
13 |
650 |
4,5 |
| 14 – 16 |
15 |
15 |
225 |
79,35 |
| 16 и более |
5 |
17 |
85 |
92,45 |
| Итого |
100 |
- |
1270 |
371 |
На основе этих данных вычислить:
1. С вероятностью 0.954 предельную ошибку выборочной средней и возможные границы, в которых ожидаются средние затраты времени на изготовление одной детали на заводе;
2. С вероятностью 0.954 предельную ошибку выборочной доли и границы удельного веса числа деталей с затратами времени на их изготовление от 10 до 14 мин.
Решение:
1. Определяем средние затраты времени на изготовление 1 детали для выборочной совокупности по формуле средней арифметической взвешенной:
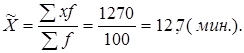
Рассчитываем дисперсию для выборочной совокупности по формуле средневзвешенной для сгруппированных данных:
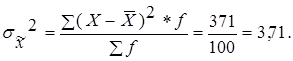
Так как выборка по условию задачи равна 10%, а n равно 100 шт., то N равно 1000 шт.Средняя ошибка выборки при бесповторном отборе рассчитывается по формуле:
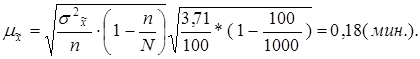
Так вероятность равна 0,954, то коэффициент доверия t равен 2. Предельная ошибка выборки определяется по формуле:
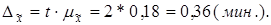
Доверительные интервалы (пределы) средней рассчитываем, исходя из двойного неравенства:
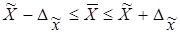 ; ;
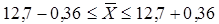 ; ; 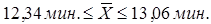
Таким образом, с вероятностью 0,954 можно утверждать, что средние затраты времени на изготовление одной детали на заводе лежат в границах от 12, 34 мин. до 13, 06 мин.
2. Определяем по выборочной совокупности долю деталей с затратами времени на их изготовление от 10 до 14 минут по формуле:
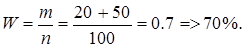
Тогда дисперсия выборочной доли равна:
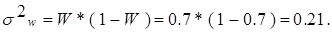
Средняя ошибка выборки определяется по аналогичной формуле, что и для выборочной средней и равна:
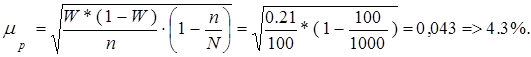
Предельная ошибка выборки для доли и доверительные интервалы определяется по формула:
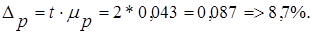
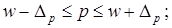 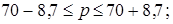 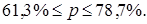 . .
Таким образом, с вероятностью 0,954 можно утверждать, что доля деталей, изготовленных с затратами времени от 10 до 14 минут составляет от 61,3% до 78,9% в общем числе деталей.
Задача № 2.2
Для определения среднего возраста 1200 студентов факультета необходимо провести выборочное обследование методом случайного бесповторного отбора. Предварительно установлено, что среднее квадратическое отклонение возраста студентов равно 3 года.
Определить количество студентов, которое нужно обследовать, чтобы с вероятностью 0,954 средняя ошибка выборки не превышала 3 года.
Решение:
Так как обследование проведено методом бесповторного отбора для определения среднего возраста студентов, то необходимый объем выборки рассчитывается по формуле:
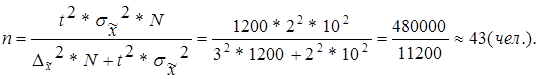
Таким образом, выборка численностью 43 человека обеспечивает заданную точность при бесповторном отборе.
2.3. Контрольные задачи
Задача № 2.1
В целях контроля за соблюдением норм расхода сырья проведено выборочное обследование партии готовой продукции. При механическом (бесповторном) способе отбора 5% изделий получены определенные данные о весе обследованных единиц, представленные в следующей таблице:
Вес изделий,
г.
|
Число образцов,
шт.
|
| до 100 |
22 |
| 100– 110 |
76 |
| 110 – 120 |
215 |
| 120 – 130 |
69 |
| 130 и свыше |
18 |
| Итого |
400 |
На основании выборочных данных вычислить:
1. По «способу моментов»:
а) средний вес изделия;
б) дисперсию.
2. Cреднее квадратическое отклонение.
3. Коэффициент вариации.
4. С вероятностью 0.997 возможные границы, в которых заключен средний вес изделий во всей партии.
5. С вероятностью 0.954 возможные границы удельного веса (доли) стандартной продукции во всей партии при условии, что к стандартной продукции относятся все изделия с весом от 100 г до 130 г.
Задача № 2.2
Для изучения возрастной структуры рабочих завода по состоянию на 1 июля было проведено 3% выборочное обследование по методу случайного бесповторного отбора. Результаты обследования распределения рабочих по возрасту представлены в следующей таблице:
Группы рабочих по возрасту,
лет.
|
Число рабочих,
чел.
|
| до 20 |
10 |
| 20 – 30 |
18 |
| 30 – 40 |
40 |
| 40 –50 |
24 |
| 50 и старше |
8 |
| Итого |
100 |
На основании данных выборочного обследования вычислите:
1. По «способу моментов»:
а) средний возраст рабочего;
б) дисперсию.
2. Среднее квадратическое отклонение.
3. Коэффициент вариации.
4. С вероятностью 0.997 возможные границы среднего возраста рабочих завода.
5. С вероятностью 0.954 возможные границы доли рабочих завода, возраст которых составляет менее 20 лет.
Задача № 2.3
При изучении производительности труда работников торговли произведено 10% -ое выборочное обследование выполнения норм выработки кассирами магазинов. В результате механического отбора получены следующие данные о распределении выборочной совокупности по выполнению норм выработки, представленные в таблице:
Выполнение норм выработки,
%
|
Число кассиров,
чел.
|
| до 90 |
3 |
| 90 – 100 |
7 |
| 100 – 110 |
30 |
| 110 – 120 |
25 |
| 120 – 130 |
17 |
| 130 – 140 |
9 |
| 140 – 150 |
6 |
| 150 и выше |
3 |
| Итого |
100 |
По данным выборки определить для генеральной совокупности:
1. С вероятностью 0.954 пределы значения доли кассиров, выполняющих норму выработки.
2. С вероятностью 0.997 пределы, в которых находится средний процент выполнения кассирами норм выработки.
Задача № 2.4
На электроламповом заводе в порядке 5% механической выборки проверено 2000 лампочек, из которых 20 забраковано. Определить с вероятностью 0,997, в каких пределах колеблется процент бракованных лампочек.
Задача № 2.5
В порядке механической 5%-ой выборки было подвергнуто испытанию на разрыв 1000 нитей из партии. Установлено, что средняя крепость пряжи равняется 340 г при среднем квадратическом отклонении 20 г. С вероятностью 0,954 определите пределы, в которых находится средняя крепость пряжи в партии.
Задача № 2.6
В городе Н с числом семей 15000 предполагается методом случайного бесповторного отбора определить долю семей с детьми ясельного возраста. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,03, если на основе предыдущих обследований известно, что дисперсия равна 0,3.
2.4. Контрольные вопросы
1. Преимущества выборочного наблюдения перед сплошным.
2. Дать определение понятий: ошибка наблюдения, ошибка регистрации, ошибка репрезентативности, максимально возможная ошибка.
3. Условия правильного отбора единиц совокупности при выборочном наблюдении.
4. Генеральная и выборочная совокупности.
5. Различия между повторной и бесповторной выборками.
6. Формулы взаимосвязи средней и предельной ошибки выборки.
7. Формулы расчета средней ошибки при повторном и бесповторном отборе.
8. Неравенства, устанавливающие возможные пределы, в которых будут находиться характеристики генеральной совокупности.
9. Формулы для расчета необходимого объема выборки.
10. Сущность теорем П.Л. Чебышева и А.М. Ляпунова.
11. Распространение результатов выборочного наблюдения на генеральную совокупность.
2.5. Тесты
1. Совокупность, из которой производится отбор единиц для выборочного наблюдения называется:
а) выборочной;
б) генеральной;
в) однородной;
г) свой ответ.
2. Виды ошибок статистических наблюдений:
а) регистрации;
б) систематические;
в) случайные;
г) репрезентативности;
д) все ответы верны.
3. По методу отбора различают:
а) бесповторный отбор;
б) случайный отбор;
в) повторный отбор;
г) все ответы верны.
4. Если количество единиц в совокупности меньше 30, то выборка считается:
а) большой;
б) малой;
в) средней;
г) нет верного ответа.
5. Виды выборок:
а) случайная;
б) типическая;
в) механическая;
г) групповая.
6. При 6%-ой выборке из партии деталей в 600 ед. объем выборки n составляет:
а) 54 ед;
б) 36 ед;
в) 46 ед.
7. Для характеристики надежности выборочных показателей различают следующие виды ошибок выборки:
а) среднюю;
б) случайную;
в) предельную;
г) репрезентативности.
8. Размер средней ошибки выборки зависит от:
а) объема выборки;
б) однородности совокупности;
в) ассиметрии;
г) степени варьирования изучаемого признака.
9. Чем больше численность выборки при прочих равных условиях, тем величина средней ошибки выборки:
а) больше;
б) меньше;
в) точнее
г) свой ответ.
10. Чем больше вариация признака, тем ______ средняя ошибка выборки:
а) больше;
б) меньше;
в) точнее;
г) свой ответ.
11. Средняя ошибка выборки показывает __________.
12. Средняя ошибка выборки имеет единицы измерения:
а) что и количественный признак;
б) не имеет единиц измерения;
в) представлена коэффициентом;
г) в процентах.
13. Для отбора единиц из неоднородной совокупности применяется:
а) типическая выборка;
б) механическая выборка;
в) собственно-случайная выборка;
г) серийная выборка.
14. Отбор единиц из генеральной совокупности посредством жеребьевки или какого-либо иного подобного способа – это:
а) типическая выборка;
б) механическая выборка;
в) собственно-случайная выборка;
г) серийная выборка.
15. Доверительные интервалы (пределы) для средней ___________.
16. Для скорости расчетов с кредиторами предприятий корпорации в коммерческом банке была проведена случайная выборка 100 платежных документов, по которым средний срок перечисления и получения денег оказался равным 22 дня со стандартным отклонением 6 дней.
Определить с вероятностью p равной 0,954 предельную ошибку выборочной средней и доверительные пределы средней продолжительности расчетов предприятий данной корпорации.
а) 1,2 дня; 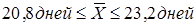 ; ;
б) 2,2 дня; 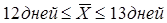 ; ;
в) 3 дня; 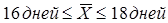 . .
17. Среди выборочного обследования 1000 семей региона по уровню душевого дохода (выборка 2%-ая, механическая) малообеспеченных оказалось 300 семей.
Определить с вероятностью 0,997 долю малообеспеченных семей во всем регионе и доверительные интервалы.
а) 2%; 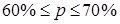 ; ;
б) 1,4%; 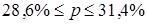 ; ;
в) 5%; 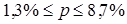 . .
18. Для определения доли рабочих со стажем работы 20 лет и более на заводе с числом рабочих 10000 была проведена механическая выборка. Определить какова должна быть численность, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,05, если на основе предыдущих обследований известно, что дисперсия равна 0,2.
а) 300 чел.;
б) 500 чел.;
в) 250 чел..
3. РЯДЫ ДИНАМИКИ
Ряд динамика представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение общественных явлений во времени. Построение и анализ рядов динамики позволяет выявить и измерить закономерности развития общественных явлений во времени.
Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней ряда: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста. Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста.
3.1. Основные формулы
Таблица 3.1 – Основные характеристики ряда динамики
| Показатель |
Цепной |
Базисный |
Абсолютный
прирост
|
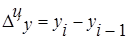 , ,
где 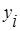 - уровень сравниваемого периода; - уровень сравниваемого периода;
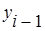 - уровень предшествующего периода. - уровень предшествующего периода.
|
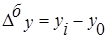 , ,
где 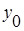 - уровень базисного периода. - уровень базисного периода.
|
Взаимосвязь: 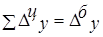 |
| Темп роста |
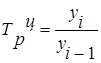 |
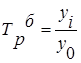 |
Взаимосвязь: 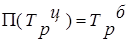 |
| Темп пророста |
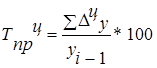 |
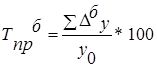 *100 *100 |
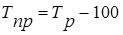 (в процентах) или (в процентах) или
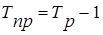 (в коэффициентах) (в коэффициентах)
|
Абсолютное
значение
одного процента
|
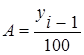 |
Таблица 3.2 – Средние показатели ряда динамики
| Показатель |
Цепной |
Базисный |
Средний
абсолютный
прирост
|
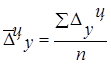 , ,
где n – число цепных абсолютных приростов в изучаемом периоде.
|
 , ,
где m – число уровней ряда динамики в изучаемом периоде, включая базисный.
|
Средний
темп роста
|
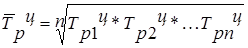 , ,
где n – число цепных коэффициентов роста;
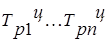 - цепные коэффициенты роста. - цепные коэффициенты роста.
|
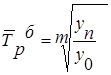
|
Темп
прироста
|
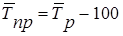 (в процентах) или (в процентах) или
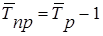 (в коэффициентах) (в коэффициентах)
|
Таблица 3.3 – Средний уровень ряда
| Ряд динамики |
Формула среднего уровня ряда |
| Для интервальных рядов динамики из абсолютных уровней |
| - при равных интервалах |
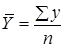 , ,
где y – абсолютные уровни ряда;
n – число уровней ряда.
|
| - при неравных интервалах |
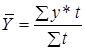 , ,
где t – веса, длительность интервалов времени между смежными датами.
|
| Для моментных рядов динамики |
| - с равностоящими уровнями |
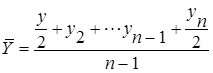 |
| - с неравностоящими уровнями |
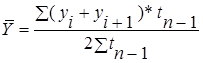 |
Таблица 3.4 – Измерение связи. Уравнения регрессии
Параметры а0
и а1
определяются из системы уравнений:
а) линейная регрессия:
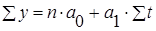 |
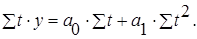 |
(3.1) |
б) парабола второго порядка:
в) гипербола:
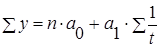 |
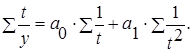 |
(3.3) |
Для определения границ интервалов прогнозируемых явлений:
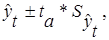 |
(3.4) |
где 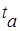 – коэффициент доверия по распределению Стьюдента; – коэффициент доверия по распределению Стьюдента;
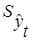 – остаточное среднее квадратическое отклонение от тренда: – остаточное среднее квадратическое отклонение от тренда:
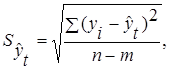 |
(3.5) |
где m – число параметров адекватной модели тренда;
n – число уровней ряда динамики.
3.2. Решение типовых задач
Задача № 3.1
Динамика производства электроэнергии в Украине характеризуется следующими данными, представленными в таблице 3.5 (столбец 1– 2):
Рассчитать:
1. Цепные и базисные аналитические показатели ряда динамики.
Проверить взаимосвязи.
2. Средние: уровень ряда, абсолютный прирост, темпы роста и прироста.
Таблица 3.5 – Исходные данные и расчетные значения
| Год |
Производство электроэнергии, млрд. кВт*ч |
Расчетные значения |
Абсолютный прирост,
млрд. кВт*ч
|
Темп роста,
%
|
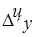 |
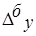 |
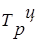 |
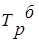 |
| 1 |
2 |
3 |
4 |
5 |
6 |
| 2001 |
957 |
– |
– |
– |
100 |
| 2002 |
876 |
876-957=-81 |
876-957=-81 |
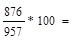 91,5 91,5 |
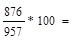 91,5 91,5 |
| 2003 |
860 |
860-876=-16 |
860-957=-97 |
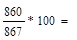 98,2 98,2 |
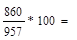 89,7 89,7 |
| 2004 |
847 |
847-860=-13 |
847-957=-110 |
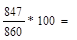 98,5 98,5 |
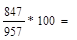 88,5 88,5 |
| 2005 |
834 |
-13 |
-123 |
98,5 |
87,1 |
| 2006 |
827 |
-7 |
-130 |
99,2 |
86,4 |
Продолжение таблицы 3.5
| Год |
Расчетные значения |
Темп прироста,
%
|
Абсолютное
значение
одного процента
прироста,
млрд. КВт*ч
|
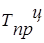 |
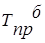 |
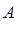 |
| 1 |
2 |
3 |
4 |
| 2001 |
– |
– |
– |
| 2002 |
91,5-100 = -8,5 |
91,5-100 = -8,5 |
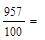 9,57 9,57 |
| 2003 |
98,2-100 = -1,8 |
89,7-100 = -10,3 |
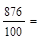 8,76 8,76 |
| 2004 |
98,5-100 = -1,5 |
88,5-100 = -11,5 |
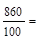 8,6 8,6 |
| 2005 |
-1,5 |
-12,9 |
8,47 |
| 2006 |
-0,8 |
-13,6 |
8,34 |
Решение:
1. Проверка взаимосвязей:
а) абсолютных приростов:
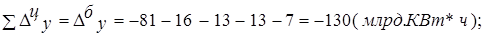
б) темпов роста:
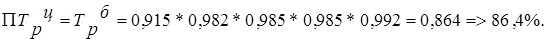
2. Так как исследуемый ряд динамики представляет собой интервальный ряд с одинаковыми интервалами, то расчет среднего размера производства электроэнергии производим по формуле:
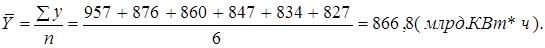
Средний абсолютный прирост рассчитывается по формулам:
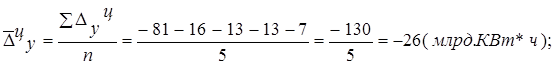
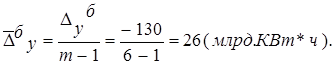
Cредний темп роста определяем по формулам:
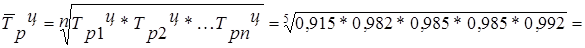
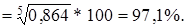
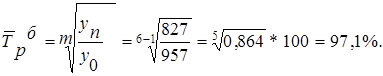
Средний темп прироста определяется по формуле:
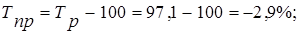
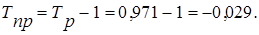
Задача № 3.2
Имеются данные об урожайности зерновых культур (исходные данные в столбцах 1 и 2):
| Месяц |
Фактическая урожайность, ц. (
y
)
|
Расчетные значения |
| t
|
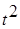 |
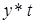 |
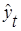 |
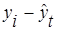 |
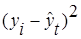 |
| Январь |
15,4 |
-9 |
81 |
-138,6 |
15,15 |
0,25 |
0,0625 |
| Февраль |
14,0 |
-7 |
49 |
-98,0 |
15,19 |
-1,19 |
1,4161 |
| Март |
17,6 |
-5 |
25 |
-88,0 |
15,23 |
2,37 |
5,6169 |
| Апрель |
15,4 |
-3 |
9 |
-46,2 |
15,28 |
0,12 |
0,0144 |
| Май |
10,9 |
-1 |
1 |
-10,9 |
15,32 |
-4,42 |
19,5364 |
| Июнь |
17,5 |
1 |
1 |
17,5 |
15,36 |
2,14 |
4,5796 |
| Июль |
15,0 |
3 |
9 |
45,0 |
15,4 |
-0,40 |
0,016 |
| Август |
18,5 |
5 |
25 |
92,5 |
15,45 |
3,05 |
9,3025 |
| Сентябрь |
14,2 |
7 |
49 |
99,4 |
15,49 |
-1,29 |
1,6641 |
| Октябрь |
14,9 |
9 |
81 |
134,1 |
15,53 |
-0,63 |
0,3969 |
| Итого |
153,4 |
0 |
330 |
6,8 |
153,4 |
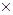 |
42,6054 |
Определить урожайность на ноябрь текущего года, построив линейную трендовую модель.
Решение:
Для выравнивания ряда используем линейную трендовую модель –
уравнение прямой: 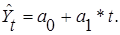
Параметры искомого уравнения прямой определяем из следующей системы нормальных уравнений:
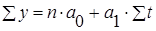
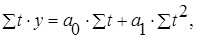 откуда откуда 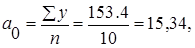
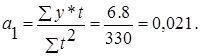
Уравнение прямой будет иметь вид: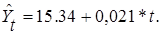
Подставляя в данной уравнение последовательно значения t, равные -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, находим выровненные уровни 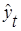 . .
Если 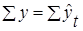 , в нашем примере эти суммы равны между собой и равны 153,4, следовательно, значения уровней выровненного ряда найдены верно. , в нашем примере эти суммы равны между собой и равны 153,4, следовательно, значения уровней выровненного ряда найдены верно.
Полученное уравнение показывает, что, несмотря на значительные колебания в отдельные годы, наблюдается тенденция увеличения урожайности зерновых культур в среднем на 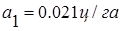 в месяц. в месяц.
Используя полученное уравнение методом экстраполяции при t равном 11, определяем ожидаемую урожайность культур на ноябрь текущего года:
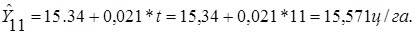
Зная точечную оценку прогнозируемого значения урожайности 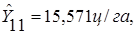 , определяем вероятностные границы интервала по формуле: , определяем вероятностные границы интервала по формуле:
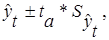 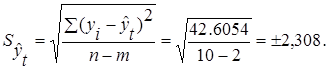
При доверительной вероятности, равной 0,95, коэффициент доверия Стьюдента равен 2,306.
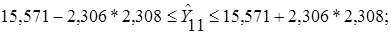
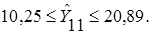
Таким образом, с вероятностью, равной 0,95, можно утверждать, что урожайность зерновых культур в ноябре текущего года будет не менее чем 10,25, но и не более чем 20,89 ц/га.
3.3. Контрольные задачи
Задача № 3.1
Динамика кредитных ресурсов коммерческого банка характеризуется следующими данными (на начало месяца, млн. у.е.), представленными в таблице:
| Месяц |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Сумма
кредитных
ресурсов
|
48 |
53 |
51 |
50 |
55 |
54 |
52 |
Определить средний объем кредитных ресурсов за 1 квартал, 2 квартал и первое полугодие.
Задача № 3.2
Стоимость основных производственных фондов предприятия выросла за период с 2003 по 2007 г. с 5,7 млн. у.е. до 8,6 млн. у.е. Численность работников увеличилась за это же время на 10%. Определить среднегодовые темпы прироста стоимости основных фондов и численности персонала.
Задача № 3.3
Представлены данные коммерческого:
| Показатели |
Предыдущий год |
Текущий год,
1 кв.
|
| 1 кв |
2 кв |
3 кв |
4 кв |
Капитал
на начало
года,
млн. у.е.
|
384 |
403 |
615 |
776 |
910 |
Прибыль
за квартал,
млн. у.е.
|
185 |
218 |
242 |
306 |
344 |
Определить:
а) виды рядов динамики;
б) среднеквартальный объем капитала;
в) постройте ряд динамики производного показателя – прибыльности капитала (определяется как отношение суммы прибыли к капиталу банка).
Задача № 3.4
Динамика импорта нефтепродуктов в регион характеризуется данными, представленными в следующей таблице:
| Год |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
Импорт,
тыс. у.е.
|
30 |
32 |
35 |
40 |
46 |
53 |
58 |
Рассчитать:
1. Цепные и базисные аналитические показатели ряда динамики. Проверить
взаимосвязи.
2. Средние: уровень ряда, абсолютный прирост, темпы роста и прироста.
Задача № 3.5
Имеются следующие данные о величине индекса потребительских цен (индекса инфляции) в Украине по месяцам за отчетный период, %:
| Месяц |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
| Индекс,% |
104,6 |
103,3 |
101,7 |
102,1 |
103,7 |
99,9 |
100,0 |
102,6 |
101,4 |
100,4 |
101,6 |
102,0 |
Определить индекс инфляции за отчетный период.
Задача № 3.6
Используя взаимосвязь показателей динамики, определить уровни производства электроэнергии в регионе и недостающие в таблице базисные показатели динамики.
Производство электроэнергии в регионе за 1998 – 2008гг. представлено в следующей таблице, млн. КВт*ч:
| Базисные показатели динамики |
| Год |
Производство э/э., млн. кВт *ч. |
Абсолютный
прирост,
млн. кВт *ч.
|
Темп
роста,
%
|
Темп
прироста,
%
|
| 1998 |
1202 |
Х |
Х |
Х |
| 1999 |
3,1 |
| 2000 |
107,6 |
| 2001 |
124 |
| 2002 |
113,7 |
| 2003 |
17,9 |
| 2004 |
290 |
| 2005 |
28,4 |
| 2006 |
133,0 |
| 2007 |
463 |
| 2008 |
41,2 |
Задача № 3.7
Используя взаимосвязь показателей динамики, определить уровни численности работников промышленности в регионе за 1999 – 2008 гг. (на конец года) и недостающие в следующей таблице цепные показатели динамики:
| Цепные показатели динамики |
| Год |
Численность работников промышленности, тыс. чел. |
Абсолютный прирост, тыс. чел. |
Темп роста, % |
Темп прироста, % |
Абсолютное значение 1% прироста, тыс. чел. |
| 1999 |
997 |
Х |
Х |
Х |
Х |
| 2000 |
36 |
| 2001 |
| 2002 |
3,1 |
10,71 |
| 2003 |
32 |
| 2004 |
| 2005 |
102,7 |
11,7 |
| 2006 |
30 |
| 2007 |
3,0 |
| 2008 |
34 |
103,2 |
Задача № 3.8
Среднегодовой темп роста производства продукции в регионе за 2002 – 2004 гг. составил 101,2%, а за 2005 – 2008 гг. – 103,5%.
Определить среднегодовой темп прироста за 2002 – 2008 гг.
Задача № 3.9
Ежегодные темпы прироста продукции на предприятии составили представлены в следующей таблице в % к предыдущему году:
| Год |
2004 |
2005 |
2006 |
2007 |
2008 |
Темп
прироста
|
3,8 |
5,3 |
4,6 |
6,2 |
5,9 |
Определить базисные темпы роста по отношению к 2003 и среднегодовой темп прироста за 2003 – 2007 гг.
Задача № 3.10
Динамика урожайности подсолнечника представлена в таблице:
| Год |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
Урожай,
ц/га
|
15,9 |
16,5 |
17,0 |
16,7 |
17,3 |
18,2 |
18,6 |
18,1 |
18,0 |
Опишите тенденцию урожайности линейным трендом.
Задача № 3.11
Имеются данные за июнь – остаток материала на складе на:
01.06 = 50 т.
03.06 = 100 т.
10.06 = 40 т.
15.06= 150 т.
21.06 = 200 т.
Определить средний остаток материала на складе за июнь.
Задача № 3.12
Имеются данные о выпуске продукции предприятием по месяцам за отчетный период, тыс. у.е.:
| Месяц |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
| Объем |
118 |
124 |
124 |
128 |
127 |
132 |
136 |
131 |
135 |
141 |
139 |
146 |
Произвести сглаживание ряда динамика методами:
1. Укрупнения периодов.
2. Скользящей средней (по 3-м месяцам).
3. Аналитического выравнивания (построив линейную функцию). Найти ожидаемый объем выпуска продукции на 01 января следующего периода.
Задача № 3.13
Рассчитать индексы сезонности на примере зарегистрированных браков за отчетный период по данным, представленным в таблице:
| Месяц |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
10 |
11 |
12 |
Итого |
| Зарегистрированные браки |
776 |
768 |
672 |
760 |
648 |
805 |
868 |
890 |
979 |
832 |
819 |
763 |
9600 |
3.4. Контрольные вопросы
1. Определение ряда динамики, основные его элементы.
2. Виды рядов динамики.
3. Условия правильного построения динамического ряда.
4. Причины возникновения несопоставимости рядов динамики.
5. Приемы для преобразования несопоставимых рядов динамики в сопоставимые.
6. Особенности расчета среднего уровня для интервального и моментного ряда динамики.
7. Основные и средние характеристики ряда динамики.
8. Сглаживание рядов динамики скользящими средними.
9. Выравнивание рядов динамики.
10. Сущность интерполяция и экстраполяция показателей.
11. Приемы и методы прогнозирования на основе рядов динамики.
12. Методы изучения сезонных колебаний.
3.5. Тесты
1. Дана численность населения, млн. чел: 2005 г. – 148,3, 2006 г. – 148,3, 2007 г. – 147,9, 2008 г. – 147,6. Определить вид ряда динамики:
а) интервальный;
б) моментный;
в) абсолютных величин;
г) с равностоящими уровнями во времени.
2. Дан объем выпуска продукции, тыс. ед.: 2005 г. – 10, 2006 г. – 14, 2007 г. – 19, 2008 г. – 16. Определить вид ряда динамики:
а) интервальный;
б) моментный;
в) абсолютных величин;
г) с неравностоящими уровнями во времени.
3. Основное условие для получения правильных выводов при анализе рядов динамики – это:
а) однородность уровней динамического ряда;
б) сопоставимость уровней динамического ряда между собой;
в) массовость данных;
г) все ответы верны.
4. Если каждый последующий уровень ряда сравнивается с предыдущим, то вычисленные показатели будут называться:
а) базисными;
б) темпами роста;
в) абсолютными приростами;
г) цепными.
5. Увеличение или уменьшение уровня ряда за определенный промежуток времени характеризует:
а) темп роста;
б) темп прироста;
в) абсолютный прирост;
г) абсолютное значение одного процента прироста.
6. Во сколько раз (%-ов) сравниваемый уровень больше – меньше базисного показывает показатель:
а) темп роста;
б) темп прироста;
в) абсолютный прирост;
г) абсолютное значение одного процента прироста.
7. Дан объем производства продукции, тыс. ед.: январь –12, февраль – 12,5, март – 13,2, апрель – 10,9, май – 11,9. Рассчитать абсолютный прирост и средний абсолютный прирост цепной и базисный, показать взаимосвязь между абсолютным цепным приростом и базисным.
8. На сколько %-ов сравниваемый уровень больше – меньше уровня, принятого за базу сравнения показывает показатель:
а) темп роста;
б) темп прироста;
в) абсолютный прирост;
г) абсолютное значение одного процента прироста.
9. Приведены затраты на продукцию, у.е.: январь – 580, февраль – 690, март – 698, апрель – 701, май – 650.
Рассчитать темп роста и средний темп роста цепной и базисный, показать взаимосвязь между темпами роста цепными и базисными.
10. Пусть имеются данные о валютном курсе: 01.01.07 г. – 25,05; 01.02.07 г. – 26,05; 01.03.07 г. – 26,75; 01.04.07 г. – 27,0. Тогда средний месячный курс валюты будет равен:
а) 25,9;
б) 26,28;
в) 27,3;
г) 21,9.
11. Если известно, что с 1-го по 15-е число месяца в банке работали 20 человек, с 16-го по 25-е – 27 человек, а с 26-го по 30–е – 30 человек, то среднеучетное число работников за месяц составит:
а) 24;
б) 23;
в) 25;
г) 26.
12. Выделяют следующие методы анализа основной тенденции развития:
а) уменьшения интервалов;
б) укрупнения интервалов;
в) смыкания рядов;
г) приведение к одному основанию;
д) аналитическое выравнивание.
13. Недостаток метода скользящей средней – это:
а) трудоемкость расчетов;
б) неточность полученных результатов;
в) потеря информации;
г) все ответы верны.
14. Метод аналитического выравнивания позволяет:
а) получить обобщенную статистическую модель тренда;
б) укрупнить интервалы;
в) оценить сезонные колебания;
г) получить прогнозное значение уровня ряда.
15. При четном числе уровня ряда равном 4, значения t будут такими:
а) -3, -1, 1, 3;
б) -4, -3, -2, -1;
в) 4, 3, 2, 1.
16. При нечетном числе уровней ряда равном 5, значения t будут такими:
а) 5, 4, 3, 2, 1;
б) -5, -4, -3, -2, -1;
в) -2, -1, 0, 1, 2.
17. Периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку – это:
а) ряд динамики;
б) сезонные колебания;
в) вариация;
г) свой ответ.
18. Нахождение уровней за пределами изучаемого ряда, т.е. продление в будущее тенденции, наблюдавшиеся в прошлом – это:
а) интерполяция;
б) экстраполяция;
в) сглаживание;
г) укрупнение.
19. В статистике нахождение показателя в середине ряда динамики, значение которого нет называется:
а) интерполяция;
б) экстраполяция;
в) сглаживание;
г) укрупнение.
Вопросы для подготовки к зачету по дисциплине «Статистика. Часть 1»
1. Предмет и методы статистики. Взаимосвязь статистики с другими науками.
2. Основные задачи статистики в условиях перехода к рыночной экономике.
3. Основные стадии статистического исследования.
4. Сущность. Задачи и организационные формы статистического наблюдения.
5. Программно- методологические вопросы плана статистического наблюдения.
6. Организационные вопросы плана статистического наблюдения.
7. Ошибки статистического наблюдения, контроль полученных данных.
8. Содержание сводки и группировки и их роль в статистическом исследовании.
9. Виды группировок и их особенности.
10. Виды и правила построения статистических таблиц.
11. Сущность, задачи и виды средних величин.
12. Средняя арифметическая.
13. Свойства средней арифметической. «Способ моментов».
14. Средняя гармоническая.
15. Структурные средние (мода и медиана).
16. Необходимость измерения вариации признаков. Размах вариаций.
17. Среднее линейное отклонение.
18. Дисперсия альтернативного признака.
19 Методы исчисления дисперсии.
20. Среднее квадратическое отклонение. Коэффициент вариации.
21. Ряды распределения, их виды и способы графического изображения.
22. Виды и формы связей.
23. Методы установление связей между явлениями.
24. Понятие о рядах динамики и основные принципы их построения.
25. Аналитические показатели ряда динамики.
26. Средний уровень ряда динамики и способы его вычисления.
27. Аналитическое выравнивание ряда динамики.
28. Экстраполяция и интерполяция.
29. Сущность индексов, их виды.
30. Основные положения теории индексов.
31. Средний арифметический и гармонический индексы.
32. Индексы переменного, постоянного состава,влияние структурных сдвигов.
33. Взаимосвязи индексов.
34. Разложение абсолютного прироста изучаемого показателя по факторам.
35. Сущность выборочного наблюдения, его достоинства и недостатки.
36. Генеральная и выборочная совокупность. Способы и схемы отбора единиц из генеральной совокупности.
37. Определение ошибки выборки для доли собственно – случайном отборе
38. Определение ошибки выборки для средней при собственно – случайном и механическом отборе.
39. Построение доверительных интервалов для средней и для доли.
40. Виды относительных показателей.
41. Графический метод изображения статистических данных.
Библиографический список
1. Украина. Законы. О государственной статистике: закон Украины // Голос Украины. – 1993. – № 2. – Ст. 56.
2. О мерах по развитию государственной статистики: указ Президента Украины от 22.11.97 г. № 1299/97 // Статистика Украины. – 1998. – № 1. –Ст.23.
3. О переходе Украины к общепринятой в международной практике системе учета и статистики: указ Президента Украины от 14.04.95 г. № 312/95 // Голос Украины. – 1999. – № 70. – Ст. 11.
4. Альбом наглядных пособий по общей теории статистики: учебн. пособие для высших с-х учеб. заведений по экон. спец. / отв.ред. С.С.Сергеев [и др.]. – М. : Фин. и статистика, 1991. – 79 с.
5. Гусаров В.М. Статистика: учебное пособие для вузов/ В.М.Гусаров. –М. : ЮНИТИ-ДАНА, 2001. – 463 с.
6. Еронова В.Н. Общая теория статистики: учебник / В.Н.Еронова, М.В.Едронова. – М. : Юрист, 2001. – 511 с.
7. Елисеева И.И. Общая теория статистики: учебник для вузов, обучающих по специальности «Статистика» / И.И.Елисеева, М.М.Юзбашева; под ред. Елисеевой И.И. – М. : Финансы и статистика, 1996. – 366 с.
8. Захошай В.Б. Статистика труда и занятости: учебно-метод. Пособие / В.Б.Захошай, А.В.Калинина; под ред. Захошай В.Б. – К. : МАУП, 2000. – 79 с.
9. Кожухарь Л.И. Основы общей теории статистики / Л.И.Кожухарь. –М. : Финансы и статистика, 2001. – 144 с.
10. Кулинич О.И. Теорiя статистики: учебник / О.И.Кулинич. – Кировоград : Держ. Центр-укр. вид-во, 1996. – 227 с.
11. Практикум по теории статистики: учеб. Пособие / отв.ред. проф. Р.А. Шмойлов [и др.]. – М. : Финансы и статистика, 2000. – 416 с.
12.Сиденко А.В. Статистика: учебник / А.В.Сиденко, Г.Ю.Попов, В.М. Матвеева; под ред. Сиденко А.В. – М. : Изд-во «Дело и Сервис», 2000. – 464 с.
13. Статистика: Сботник задач: учеб. пособие для экон. вузов и фак. / отв.ред. А.В.Головач [и др.]. – К. : Вища шк., 1994. – 445 с.
14. Статистика: учебник / отв.ред. С.С.Герасименко [и др.]. – К. : КНЭУ, 2000. – 450 c.
15. Теория статистики: учебник / отв.ред. Г.Л.Громыко [и др.]. – М. : Инфра – М, 2002. – 414 с.
16. Теория статистики: учебник / отв.ред. Р.А.Шмойлов [и др.]. – 3-е изд., перер. – М. : Финансы и статистика, 2001. – 240 c.
17. Эрина А.М. Теория статистики: практикум / А.М.Эрина, З.О.Пальям; под ред. Эрина А.М. – К. : Знання, 2002. – 323 с.
Заказ № _____ от «___»________20___г. Тираж ________ экз.
Изд-во СевНТУ
|