Тульский Институт Экономики и Информатики
Кафедра экономики и менеджмента
Контрольная работа
по дисциплине «Планирование и прогнозирование в условиях рынка»
Вариант №
6
Выполнил: ст.гр. ПИвЭ05
Андрианова К. Г.
Проверил: Глухарев Ю.Г.
Тула 2009
Задание............................................................................................................. 3
Решение............................................................................................................ 3
Вывод............................................................................................................... 7
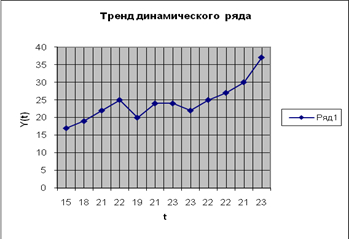
Выровнять динамический ряд по линейной зависимости.
| Y(t) |
17 |
19 |
22 |
25 |
20 |
24 |
24 |
22 |
25 |
27 |
30 |
37 |
| t |
15 |
18 |
21 |
22 |
19 |
21 |
23 |
23 |
22 |
22 |
21 |
23 |
Определить:
а) график зависимости переменной y
(
t
)
и t
по заданным параметрам;
б) неизвестные параметры а
и в
;
в) тесноту связи между y
(
t
)
и t
;
г) значимость коэффициента корреляции для линейной зависимости;
д) точность аппроксимации;
е) значение критериев автокорреляции остатков.
Решение
а) Построим график зависимости переменной y
(
t
)
и t
по заданным параметрам:
| Y(t) |
17 |
19 |
22 |
25 |
20 |
24 |
24 |
22 |
25 |
27 |
30 |
37 |
| t |
15 |
18 |
21 |
22 |
19 |
21 |
23 |
23 |
22 |
22 |
21 |
23 |
| №
|
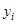 |
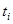 |
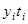 |
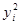 |
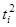 |
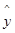 |
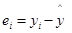 |
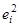 |
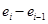 |
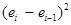 |
| 1 |
17 |
15 |
255 |
289 |
225 |
15,8429 |
1,1571 |
1,3388 |
| 2 |
19 |
18 |
342 |
361 |
324 |
20,2094 |
-1,2094 |
1,4627 |
-2,3665 |
5,6003 |
| 3 |
22 |
21 |
462 |
484 |
441 |
24,5759 |
-2,5759 |
6,6353 |
-1,3665 |
1,8673 |
| 4 |
25 |
22 |
550 |
625 |
484 |
26,0314 |
-1,0314 |
1,0638 |
1,5445 |
2,3855 |
| 5 |
20 |
19 |
380 |
400 |
361 |
21,6649 |
-1,6649 |
2,7720 |
-0,6335 |
0,4013 |
| 6 |
24 |
21 |
504 |
576 |
441 |
24,5759 |
-0,5759 |
0,3317 |
1,0890 |
1,1859 |
| 7 |
24 |
23 |
552 |
576 |
529 |
27,4869 |
-3,4869 |
12,158 |
-2,9110 |
8,4739 |
| 8 |
22 |
23 |
506 |
484 |
529 |
27,4869 |
-5,4869 |
30,106 |
-2,0000 |
4,0000 |
| 9 |
25 |
22 |
550 |
625 |
484 |
26,0314 |
-1,0314 |
1,0638 |
4,4555 |
19,8515 |
| 10 |
27 |
22 |
594 |
729 |
484 |
26,0314 |
0,9686 |
0,9382 |
2,0000 |
4,0000 |
| 11 |
30 |
21 |
630 |
900 |
441 |
24,5759 |
5,4241 |
29,421 |
4,4555 |
19,8515 |
| 12 |
37 |
23 |
851 |
1369 |
529 |
27,4869 |
9,5131 |
90,499 |
4,0890 |
16,7200 |
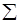 |
292 |
250 |
6176 |
7418 |
5272 |
292,0000 |
0,0000 |
177,79 |
8,3560 |
84,3371 |
| Ср.зн. |
24,333 |
20,833 |
514,6667
|
618,1667
|
439,333 |
24,3333 |
б) Найдем решение системы уравнений
 для определения параметров а
и в. для определения параметров а
и в.
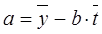 , , 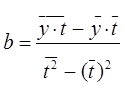
b=1,455497, a=-5,989529
Определим дисперсию и среднеквадратическое отклонение по выборке y
(
t
)
иt
:
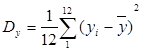 , , 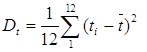
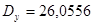 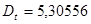
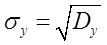 , , 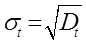 
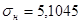 ,
, 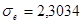 . .
в) Определим тесноту связи между двумя СВ y
(
t
)
и t
при нелинейной зависимости между ними с помощью корреляционного отношения:
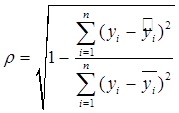
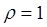 . .
Т.к. корреляционное отношение всегда положительно 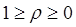 , то чем теснее связь между y
(
t
)
и t
, тем больше значение корреляционного отношения. , то чем теснее связь между y
(
t
)
и t
, тем больше значение корреляционного отношения.
г) Найдем значимость коэффициента корреляции для линейной зависимости:
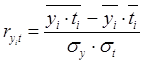
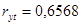
Т.к. коэффициента корреляции 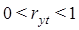 , то найденное нами значение коэффициента корреляции 0,6568 > 0 и имеет место прямой зависимости между переменной y
(
t
)
и t
. , то найденное нами значение коэффициента корреляции 0,6568 > 0 и имеет место прямой зависимости между переменной y
(
t
)
и t
.
д) Определим точность аппроксимации
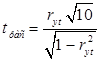 : :
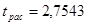
По таблице распределения Стьюдента по значению степеней свободы равной 10-ти
и значении 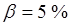 определим теоретическое значение определим теоретическое значение 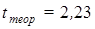 . Т.к. . Т.к. 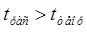 , то ошибка аппроксимации отсутствует. , то ошибка аппроксимации отсутствует.
е) Найдем значение d-критерия автокорреляцию с помощью метода Дарбина-Уотсона:
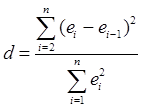
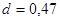 , ,
таким образом, автокорреляция остатков отсутствует.
Вывод
В результате контрольной работы мы выровняли динамический ряд по линейной зависимости, определили неизвестные параметры а
и в
, корреляционное отношение критерий автокорреляции и точность аппроксимации. В нашей модели отсутствует автокорреляция остатков. Поэтому регрессионная модель имеет высокий уровень адекватности и является наиболее правильной спецификацией парной регрессии заданной выборкой.
|