Содержание
Введение
1 Оптимизационные методы решения экономических задач.
2 Многокритериальная оптимизация. Методы сведения многокритериальной задачи к однокритериальной
3 Гладкая оптимизация.
4 Выпуклая оптимизация. Условие выпуклости.
5 Экономико-математическая модель реструктуризации угольной промышленности. Критерий оптимизационной задачи
Заключение
Литература
Введение
Угольная промышленность является одной из базовых в народно-хозяйственном комплексе Украины. Уголь потребляется почти во всех отраслях народного хозяйства и определяет в основном темпы и возможный уровень развития производства черных и цветных металлов, электрической и тепловой энергии, других отраслей промышленности. Каменный и бурый уголь служат исходным сырьем для ряда отраслей химической промышленности.
Вследствие большой глубины угольных залежей и небольшой мощности пластов угольная промышленность Украины имеет худшие показатели добычи угля по сравнению с некоторыми странами СНГ и мира. Добыча угля в осуществляется в несоизмеримо худших горно-геологических условиях, чем в других странах мира. Это - главная объективная причина больших удельных затрат материальных, энергетических, трудовых ресурсов, а также того, что производительность труда намного ниже мировой. Кроме того, отрасль теряет наиболее подготовленных, квалифицированных специалистов. Большая часть шахт нерентабельна, т.е. суммарные затраты на добычу угля превышают его стоимость на рынке.
В настоящее время отрасль требует внедрения задач оптимизационного типа, в которых требуется найти наилучшее или оптимальное решение при заданных условиях производства. Опыт западноевропейских государств, практически завершивших оптимизационный процесс в угольной промышленности, и России, стартовые позиции которой сходны с Украиной, подтверждает необходимость поддержки и контроля со стороны государства при реализации намеченных программ.
Таким образом, необходимо отметить, что изучение экономических задач оптимизационного типа относящихся к угольной промышленности является актуальным предметом исследования. Наличие большого количества проблем требует детального их изучения и разработки направлений по их решению.
Реклама

1 Оптимизационные методы решения экономических задач
К экономическим задачам оптимизационного типа относятся задачи, в которых требуется найти наилучшее или оптимальное решение при заданных условиях производства. Такие задачи называются задачами на максимум или минимум. Особенностью задач оптимизационного типа является многовариантность их решений, обусловленная следующими причинами: взаимозаменяемостью ресурсов; взаимозаменяемостью готовых видов продукции; существованием альтернативных технологий производства; неодинаковостью технико-экономических показателей даже однотипных хозяйственных субъектов.
Возможны два подхода к постановке оптимизационных задач: при первом подходе требуется получить максимальные конечные результаты при заданных условиях производства; при втором подходе требуется получить заданные конечные результаты при минимальных затратах ресурсов.
Математический инструментарий, позволяющий решать экономические задачи оптимального типа, называется программированием. Различают линейное и нелинейное программирование.
На практике наибольшее распространение получило линейное программирование.
Методы линейного программирования в математике известны под названием общей задачи линейного программирования. Аналитическая формулировка общей задачи линейного программирования. Общая задача линейного программирования формулируется следующим образом:
Найти решение {Х1
,Х2
,….Хn
}, позволяющее максимизировать или минимизировать целевую функцию
F = C1
X1
+C2
X2
+…+ Cn
Xn
при условиях
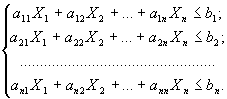
Х1
≥0; Х2
≥0; …; Хn
≥0.
Это развернутая запись общей задачи линейного программирования. Сокращенная запись этой модели имеет вид:
Найти решение {Xj
}, позволяющее максимизировать (минимизировать) функцию
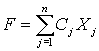
при условиях
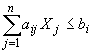 , i = 1,2,…,n;
, i = 1,2,…,n;
Xj
≥ 0, j = 1,2,…,n.
Вышеприведенные записи общей задачи линейного программирования называют аналитической формой записи.
Любое решение, удовлетворяющее условиям, называется допустимым решением. Допустимое решение систем неравенств, удовлетворяющее целевой функции, называется оптимальным решением. Такое решение единственно при заданных условиях.
Матричная форма записи общей задачи линейного программирования
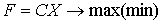
при ограничениях AX≤B
X≥0
где С = (с1
, с2
,…, сn
);
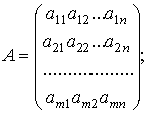
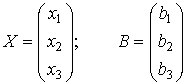
где С – матрица-строка
А – матрица системы
Х – матрица-столбец переменных
В – матрица-столбец свободных членов
2 Многокритериальная оптимизация. Методы сведения многокритериальной задачи к однокритериальной.
Реклама

Многокритериальная оптимизация представляет собой минимизацию некого вектора целей F(x), на которой могут быть наложены дополнительные ограничения или предельные значения
Отметим, что поскольку F(x) является неким вектором, то любые компоненты F(x) являюся конкурирующими и отсутсвует некое единое решение поставленной задачи. Взамен этого, для описания характеристик целей вводится концепция множества точек неулучшаемых решений (так называемая оптимальность по Парето).Неухудшаемое решение есть такое решение, в котором улучшение в одной из целей приводит к некому ослаблению другой. Для более точной формулировки данной концепции рассмотрим некую область допустимых решений 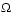 в параметрическом пространстве в параметрическом пространстве 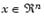 , которое удовлетворяет всем принятым ограничениям. , которое удовлетворяет всем принятым ограничениям.
Отсюда возможно определить соответствующую область допустимых решений для пространства целевых функций 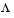 . .
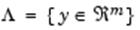 , где , где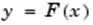
при условии 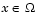
Определение. Точка 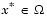 является неулучшаемым решением, если для некоторой окрестности является неулучшаемым решением, если для некоторой окрестности 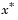 нет некого нет некого  такого, что такого, что 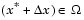
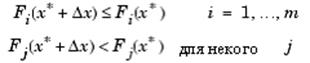
Стратегия взвешенных сумм
Данная стратегия взвешенных сумм преобразует многокритериальную задачу минимизации вектора 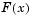 в некую скалярную задачу путем построения неких взвешенных сумм для всех выбранных объектов. в некую скалярную задачу путем построения неких взвешенных сумм для всех выбранных объектов.
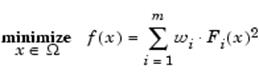
Далее уже к данной задаче оптимизации уже может быть применен стандартный алгоритм оптимизации без наличия ограничений. В этом случае рассматриваются взвешенные коэффициенты для каждой из выбранных целей. Взвешенные коэффициенты необязательно должны напрямую соответствовать относительной значимости соответствующей цели или принимать во внимание взаимовлияние между конкретно выбранными целями. Более того, границы неулучшаемых решений могут быть и не достигнуты, так что определенные решения являются по существу недостижимыми.
Метод  -ограничений -ограничений
Некий определенный способ, который отчасти позволяет преодолеть проблему выпуклости метода взвешенных сумм, есть метод 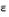 -ограничений. В этом случае осуществляется минимизация основной цели -ограничений. В этом случае осуществляется минимизация основной цели  и при представлении остальных целей в форме ограничений типа неравенств. и при представлении остальных целей в форме ограничений типа неравенств.
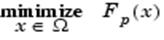
при выполнении условия
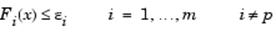
Подобный подход позволяет определить некое количество неулучшаемых решений для случая вогнутой границы, что, по существу, является недоступным в методе взвешенных сумм, например, в точке искомого решения 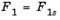 и и 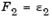 . Однако проблемой данного метода является подходящий выбор . Однако проблемой данного метода является подходящий выбор 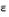 , который мог бы гарантировать допустимость некого решения. , который мог бы гарантировать допустимость некого решения.
Метод достижения цели
Описанный далее метод представляет собой метод достижения цели Гембики. Данный метод включает в себя выражение для множества намерений разработчика 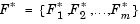 , которое связано с множеством целей , которое связано с множеством целей 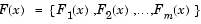 . Такая формулировка задачи допускает, что цели могут быть или недо- или передостижимыми, и что дает разработчику возможность относительно точно выразить исходные намерения. Относительная степень недо- или передостижимости поставленных намерений контролируется посредством вектора взвешенных коэффициентов . Такая формулировка задачи допускает, что цели могут быть или недо- или передостижимыми, и что дает разработчику возможность относительно точно выразить исходные намерения. Относительная степень недо- или передостижимости поставленных намерений контролируется посредством вектора взвешенных коэффициентов 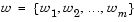 и может быть представлена как стандартная задача оптимизации с помощью следующей формулировки и может быть представлена как стандартная задача оптимизации с помощью следующей формулировки
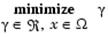
При условии, что
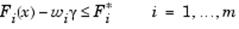
Член 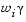 вносит в данную задачу элемент ослабления, что, иначе говоря, обозначает жесткость заданного намерения. Весовой вектор w дает исследователю возможность достаточно точно выразить меру взаимосвязи между двумя целями. Например, установка весового вектора w как равного исходному намерению указывает на то, что достигнут тот же самый процент недо- или передостижимости цели вносит в данную задачу элемент ослабления, что, иначе говоря, обозначает жесткость заданного намерения. Весовой вектор w дает исследователю возможность достаточно точно выразить меру взаимосвязи между двумя целями. Например, установка весового вектора w как равного исходному намерению указывает на то, что достигнут тот же самый процент недо- или передостижимости цели 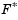 . Посредством установки в ноль отдельного весового коэффициента (т.е. . Посредством установки в ноль отдельного весового коэффициента (т.е. 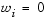 ) можно внести жесткие ограничения в поставленную задачу. Метод достижения цели обеспечивает подходящую интуитивную интерпретацию поставленной исследовательской задачи и которая, в свою очередь, является вполне разрешимой с помощью стандартных процедур оптимизации. ) можно внести жесткие ограничения в поставленную задачу. Метод достижения цели обеспечивает подходящую интуитивную интерпретацию поставленной исследовательской задачи и которая, в свою очередь, является вполне разрешимой с помощью стандартных процедур оптимизации.
3 Гладкая оптимизация.
Метод множителей Лагранжа позволяет отыскивать максимум или минимум функции при ограничениях-равенствах. Основная идея метода состоит в переходе от задачи на условный экстремум к задаче отыскания безусловного экстремума некоторой построенной функции Лагранжа. Пусть задана задача НП при ограничениях-равенствах вида
минимизировать 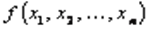
при ограничениях
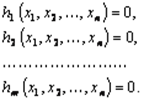
Предположим, что все функции 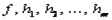 – дифференцируемы. Введем набор переменных
– дифференцируемы. Введем набор переменных 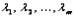 (число которых равняется числу ограничений), которые называются множителями Лагранжа, и составим функцию Лагранжа такого вида:
(число которых равняется числу ограничений), которые называются множителями Лагранжа, и составим функцию Лагранжа такого вида:
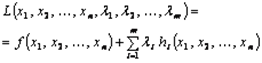
Справедливо такое утверждение для того чтобы вектор 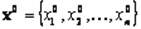 являлся решением задачи при ограничениях необходимо, чтобы существовал такой вектор
являлся решением задачи при ограничениях необходимо, чтобы существовал такой вектор 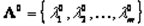 , что пара векторов удовлетворяла бы системе уравнений
, что пара векторов удовлетворяла бы системе уравнений
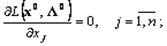
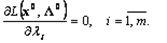
множителей Лагранжа, который состоит из следующих шагов.
Составляют функцию Лагранжа 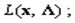
Находят частные производные 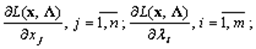
Решают систему уравнений
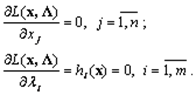
и отыскивают точки 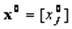 , удовлетворяющие системе.
, удовлетворяющие системе.
Найденные точки 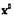 дальше исследуют на максимум (или минимум).
дальше исследуют на максимум (или минимум).
Седловая точка и задача нелинейного программирования
Рассмотрим функцию Лагранжа 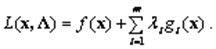
Определение Пара векторов 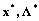 называется седловой точкой функции Лагранжа
называется седловой точкой функции Лагранжа 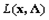 , если при всех
, если при всех 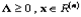 выполняется условие
выполняется условие
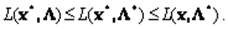
Неравенство называют неравенством для седловой точки. Очевидно, что в седловой точке выполняется условие
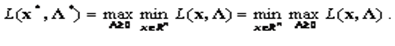
Между понятием седловой точки функции Лагранжа  и решением задачи НП существует взаимосвязь, которая устанавливается в следующей теореме.
и решением задачи НП существует взаимосвязь, которая устанавливается в следующей теореме.
Теорема. Пусть 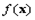 и все
и все 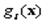 выпуклы и функции
выпуклы и функции 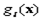 удовлетворяют условию регулярности Слейтера. Вектор
удовлетворяют условию регулярности Слейтера. Вектор 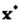 является решением задачи НП тогда и только тогда, когда существует такой вектор
является решением задачи НП тогда и только тогда, когда существует такой вектор 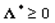 , что
, что
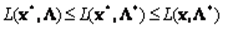
Теорема Куна-Таккера. Пусть функции 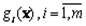 , имеют непрерывные частные производные на некотором открытом множестве
, имеют непрерывные частные производные на некотором открытом множестве 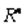 , содержащем точку
, содержащем точку 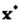 . Если
. Если 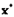 является точкой минимума функции
является точкой минимума функции 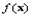 при ограничениях
при ограничениях 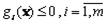 , удовлетворяющих условию регулярности в виде линейной независимости векторов
, удовлетворяющих условию регулярности в виде линейной независимости векторов  , то существуют такие неотрицательные множители Лагранжа
, то существуют такие неотрицательные множители Лагранжа 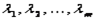 , что
, что
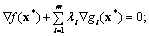
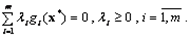
Определим функцию Лагранжа следующим образом:
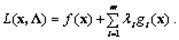
Тогда теорему Куна-Таккера можно записать в виде
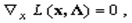
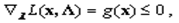
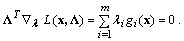
Заметим, что множители Лагранжа 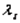 в задаче НП с ограничениями-равенствами являются знаконеопределенными, тогда как в теореме Куна-Таккера они должны быть положительными.
в задаче НП с ограничениями-равенствами являются знаконеопределенными, тогда как в теореме Куна-Таккера они должны быть положительными.
Каждой задаче линейного программирования соответствует двойственная задача. Двойственная задача по отношению к исходной задаче строится по следующим правилам:
· Если исходная задача ставится на максимум, то двойственная ставится на минимум и наоборот.
· Коэффициенты целевой функции исходной задачи становятся правыми частями ограничений двойственной задачи. Правые части ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи.
· Если A-матрица коэффициентов исходной задачи, то транспонированная матрица T A будет матрицей коэффициентов двойственной задачи.
· В задаче на максимум все ограничения имеют знак ≤ (=), а в задаче на минимум все ограничения имеют знак ≥ .
· Число переменных в двойственной задаче равно числу ограничений в исходной задаче. Каждому ограничению исходной задачи соответствует переменная двойственной задачи. Если ограничение исходной задач имеет знак (≥ ), то соответствующая переменная двойственной задачи неотрицательна. Если ограничение имеет знак (=), то соответствующая переменная двойственной задачи может принимать положительные и отрицательные значения и наоборот.
4 Выпуклая оптимизация. Условие выпуклости
Основная задача выпуклого программирования
Пусть задано выпуклое и замкнутое множество 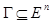 . Рассмотрим множество . Рассмотрим множество
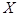 ={ ={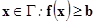 }, }, 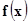 =( =(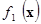 ,…, ,…,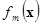 ), ), 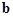 Î
Î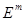 . .
где 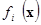 ( (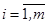 ) — вогнутые (выпуклые вверх) непрерывные на ) — вогнутые (выпуклые вверх) непрерывные на 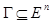 скалярные функции. В теории математического программирования каждый элемент скалярные функции. В теории математического программирования каждый элемент 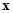 Î Î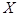 принято называть допустимым планом, а само множество принято называть допустимым планом, а само множество 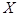 — множеством допустимых планов. — множеством допустимых планов.
Формальная постановка задачи выпуклого программирования
Задачу
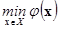 , ,
где 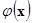 выпукла, а выпукла, а 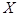 определяется вышеприведенными условиями, называется основной задачей выпуклого программирования. определяется вышеприведенными условиями, называется основной задачей выпуклого программирования.
0 означает, что ставится задача:
Если существует минимальное значение функции 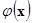 на множестве на множестве 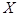 , то среди всех допустимых планов найти оптимальный план , то среди всех допустимых планов найти оптимальный план 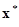 , для которого , для которого
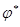 = =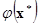 = =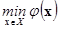
при этом число 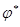 называют значением задачи. называют значением задачи.
Если оптимального плана не существует, то требуется
· либо найти значение задачи как точную нижнюю грань значений функции 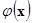 на множестве на множестве 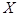 : :
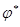 = =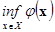
· либо убедиться, что 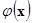 неограничена снизу на множестве неограничена снизу на множестве 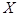 ; ;
· либо убедиться в том, что множество допустимых планов 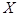 пусто. пусто.
Для решения предложенной оптимизационной задачи следует выполнить следующие действия:
· Определить множество 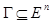 . .
· Определить вектор-функцию 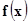 =( =(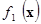 ,…, ,…,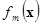 ) и вектор ) и вектор 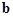 Î Î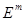 . .
· Определить множество допустимых планов 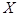 ={ ={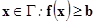 }. }.
· Привести задачу к стандартной форме основной задачи выпуклого программирования и определить оптимизируемую функцию 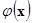 . .
· Проверить, является ли полученная оптимизационная задача ЗВП, для этого
· проверить на выпуклость множество 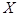 ; ;
· проверить на выпуклость функцию 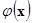 . .
В случае успеха п.
· Построить функцию Лагранжа полученной ЗВП.
· С помощью дифференциальных условий Куна-Таккера найти седловые точки построенной функции Лагранжа.
В случае неудачи п. попытаться найти другие методы решения задачи.
Методы субградиентной оптимизации. Эти итеративные процедуры формируют последовательность векторов {lk
}.
Фундаментальный теоретический результат заключается в том, что
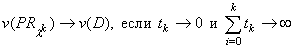 . .
Размер шага на практике обычно выбирают, следуя ,
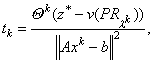
где q k
— скаляр, 0 < q k
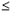 2 и z* — верхняя граница для n(D). Обычно z* получают эвристикой для P. В методе ветвей и границ z* — текущий рекорд. Последовательность q k
, как правило, начинается с q 0
=2 и затем q k
делится пополам, через фиксированное число итераций, зависящее от размерности задачи. 2 и z* — верхняя граница для n(D). Обычно z* получают эвристикой для P. В методе ветвей и границ z* — текущий рекорд. Последовательность q k
, как правило, начинается с q 0
=2 и затем q k
делится пополам, через фиксированное число итераций, зависящее от размерности задачи.
5 Экономико-математическая модель реструктуризации угольной промышленности. Критерий оптимизационной задачи
В связи с резким сокращением объемов капитальных вложений со стороны государства в угольную промышленность и отработкой запасов угля на шахтах, для выхода из кризисного состояния угольной промышленности, проводится ее оптимизация. Как известно, в результате ликвидации горных предприятий возникает ряд проблем, среди них наиболее острые социально-экономические. Эти проблемы необходимо решать путем усовершенствования нормативно-технической документации по проведению реструктуризации угольной промышленности Украины.
Одним из разрабатываемых вариантов совершенствования нормативной документации и создания на ее основе обобщенного руководства по оптимизации угольной промышленности, является создание экономико-математической модели ликвидации горного предприятия. По результатам решения оптимизационной задачи, описанной данной моделью, будут сделаны конкретные предложения по совершенствованию существующей нормативной базы реструктуризации.
Данная модель представляет собой задачу линейного программирования, в которой будет определено количество необходимых бюджетных затрат для осуществления мероприятий по ликвидации горных предприятий по различным направлениям.
Полученная модель основана на одной из существующих математических моделей на уровне отраслей промышленности. Эта модель - «Модель распределения капитальных вложений на переходящие и вновь начинаемые объекты строительства». При использовании этой модели можно получить значения капитальных вложений по годам планового периода для переходящих и вновь начинаемых объектов строительства. В данном случае решается задача оптимального распределения лимита капитальных вложений по объектам строительства таким образом, чтобы повысить экономическую эффективность плана капитального строительства и вовремя ввести необходимые мощности.
Проанализировав вышеназванную модель, в качестве критерия оптимизации в разрабатываемой модели реструктуризации угольной промышленности была принята экономическая эффективность ликвидации горного предприятия.
Постановка оптимизационной задачи в нашем случае делается на основе следующих условий:
1) При ликвидации шахты возникают различные затраты, осуществляемые за счет государственного финансирования, их можно укрупнено разделить по нескольким направлениям;
2) Отчетность о проведении работ по ликвидации предприятий компания«Укруглереструктуризация» предоставляет за определенные периоды времени, следовательно, финансирование осуществляется через равномерные периоды времени;
3) За счет того, что убыточная шахта перестает работать, возникает экономия бюджетных средств, направленных на поддержание шахт погашение их убытков путем выплат дотаций;
4) Расходы по различным направлениям ликвидации шахт проектируются на основании сметной стоимости производства определенных работ по закрытию шахт; эта сметная стоимость рассчитывается по существующим нормативным документам;
5) Необходимо учесть, что бюджетное финансирование лимитировано в каждом периоде;
6) Затраты по каждому направлению ликвидации горного предприятия недолжны превышать суммарную сметную стоимость;
7) Отдельно необходимо учесть обеспечение социальной защиты, высвобождаемых работников.
Целевая функция полученной математической модели с учетом критерии экономической эффективности ликвидации горного предприятия сформулирована следующим образом:
F=ΣΣ(1+E)t-1
Qi
→max
где i - направление ликвидационных затрат;
t - период осуществления затрат;
xi
- затраты на ликвидацию;
Pu
-экономия в результате ликвидации шахт за счет отсутствия дотаций на покрытие убытков;
(1+E)t-1
- коэффициент дисконтирования полученной экономии к моменту возникновения затрат;
Qi
- суммарная сметная стоимость проведения работ по закрытию шахты по определенному направлению.
Так как модель находится в процессе разработки, то ограничения в задаче еще окончательно не сформулированы. Хотя уже на данный момент принято, что среди ограничений будут лимит бюджетного финансирования (Ki
) и сметная стоимость:
ΣXu
≤Ki
ΣXu
≤Qi
Решение оптимизационной задачи по полученной модели реструктуризации угольной промышленности покажет, сколько по какому направлению ликвидации горного предприятия необходимо средств и как их распределить. Предполагается, что наибольший вес, в качестве ограничений, внесут затраты на социальные нужды. Они же будут вступать в противоречие с целевой функцией задачи (сокращение затрат на ликвидацию предприятий не должно проводиться за счет социальной сферы).Компромисс будет найден путем изменения величины суммарной сметной стоимости.
Заключение
Угольная промышленность занимает важное место в народнохозяйственном комплексе Украины. Она обеспечивает национальную безопасность в топливной сфере, предоставляет сырье для металлургической и химической промышленности, электроэнергетики.
На территории Украины выделяют три основных угольных бассейна: Донецкий каменноугольный бассейн, Львовско-Волынский каменноугольный бассейн Приднепровский буроугольный бассейн. Однако основным местом добычи можно считать Донбасс.
Проблемы развития угольной промышленности Украины, и, в частности, Донбасса являются общегосударственными и меры по их решению должны определяться Национальной государственной программой. В процессе реализации которой в Донбассе должен ослабится демографический и экологический пресс.
Оценка мирового опыта процесса реструктуризации угольной промышленности показала, что это сложный экономический процесс и он был необходим. В Украине при его проведении было допущено много негативных явлений: он сводился в основном к закрытию шахт и не всегда научно обосновано; отсутствовали средства для проведения внутренней реструктуризации на действующих шахтах. Поэтому, для придания реструктуризации системного характера, необходимо внести дополнения к Указу Президента Украины «О разработке Энергетической стратегии Украины на период до 2030 г. и на дальнейшую перспективу», в которых бы определилась необходимость разработки в рамках Стратегии отдельной программы реструктуризации угольной промышленности.
Увеличение стоимости ликвидации шахт в настоящее время по сравнению с 70—80-ми годами в определенной мере объясняется некоторым изменением Правил безопасности, соответствующих инструкций к ним и другими нормативными документами. Однако многие виды работ, закладываемые в проекты, по нашему мнению, не обязательны. Сопоставление показывает, что средние расходы на ликвидацию представительной шахты составляют примерно 80 млн. грн., тогда как в прошлые годы они были 10 млн. грн. Даже с учетом принятия ужесточенных требований действующих нормативных документов затраты на ликвидацию одной шахты можно снизить в несколько раз.
При реформировании, прогнозировании развития топливно-энергетического комплекса страны следует учитывать мировые тенденции разработки и применения принципиально новых технологий, радикально повышающих эффективность извлечения, переработки и использования угля, а также производства из добытого угля облагороженного, экологически чистого топлива, промышленного использования шахтного метана.
Необходимо разрабатывать на государственном уровне комплексные долгосрочные программы по энерготехнологиям, предусматривающим совместное научно-техническое и организационно-финансовое разрешение проблем угольной промышленности и энергетики.
Интеграция Украины в ЕС потребует проведения радикальных мер по повышению конкурентоспособности отечественной угольной промышленности путем ускорения ее реструктуризации, технической модернизации и финансового оздоровления. Необходимо временно существенно увеличить бюджетное финансирование отрасли, чтобы на пороге вступления в ЕС она могла нормально функционировать, в дальнейшем уменьшая свою финансовую зависимость от госбюджета. Было бы нежелательно, чтобы, интегрируясь в ЕС, Украина была вынуждена отказаться от намеченного наращивания и тем более пойти на уменьшение объемов производства угольной продукции, так как это создало бы определенные угрозы для ее энергетической безопасности.
Таким образом, представляется целесообразным разработать, и утвердить Министерством топлива и энергетики или Кабинетом Министров Украины ряд пормативно-правовых документов, в которых изложенные вопросы нашли бы свое решение. Оптимизационные методы и ЭКОНОМИКО-МАТЕМАТИЧЕСКие МОДЕЛи РЕСТРУКТУРИЗАЦИИ УГОЛЬНОЙ ПРОМЫШЛЕННОСТИ
Литература
1. Дорохов В. А., Шевцов Н. Р., Фам Ван Лам. Современное состояние сзакрытием шахт в угольной отрасли Украины /Сборник трудов кафедры СШ иПС, ДонНТУ - Донецк, 2001
2. Шевцов Н. Р. Современное состояние и перспективы развития проблемызакрытия шахт /Сборник трудов кафедры СШ и ПС, ДонНТУ - Донецк, 2001
3. Крушевский А. В. Справочник по экономико-математическим моделям иметодам. – Киев: Техника,1982. – 208с.
4. Агафонов Г.В., Орехова Л.Н., Санеев Б.Г., Соколов А.Д. Методы и модели оптимизации развития систем угольной промышленности //Беляев Л.С., Воропай Н.И., Кононов Ю.Д. и др. Методы исследования и управления системами энергетики /Под ред. Меренкова А.П. и Руденко Ю.Н. - Новосибирск, Наука, 1987, - 476c.
5. Агафонов Г.В., Орехова Л.Н., Попов С.П., Соколов А.Д. Автоматизированное рабочее место исследователя перспектив развития угольных бассейнов // Технология программирования 90-х: Тез.докл. междунар. конференции-ярмарки. - Киев, 1991. - С. 140-141.
|