КАБИНЕТ МИНИСТРОВ УКРАИНЫ
ЮЖНЫЙ ФИЛИАЛ
НАЦИОНАЛЬНОГО УНИВЕРСИТЕТА БИОРЕСУРСОВ и ПРИРОДОПОЛЬЗОВАНИЯ УКРАИНЫ
"КРЫМСКИЙ АГРОТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ"
Факультет экономический
Кафедра прикладной математики и экономической кибернетики
КУРСОВАЯ РАБОТА
по дисциплине моделирование экономики
на тему: МОДЕЛЬ ЭКСПЕРТНОЙ ОЦЕНКИ
Выполнила:
Студентка 4 курса группы ЭК-43
Антипкина Т. Н.
Проверил: доцент кафедры прикладной математики и экономической кибернетики
Степанов А. В.
Cимферополь, 2010
СОДЕРЖАНИЕ
Введение
1. Содержательная постановка задачи
2. Формальная постановка задачи
3. Математические методы решения
4. Описание алгоритма
4.1 Определение победителя Борда
4.2 Нахождение оценки Копленда
4.3 Алгоритм определения победителя за правилами Борда или Копленда
5. Описание программы
5.1 Выбор технологии программирования
5.2 Структура программы
5.3 Инструкция пользователю
6. Контрольный пример
Выводы
Список литературы
Дополнения
Введение
"Демократия как метод управления использует результаты общественных решений граждан на выборах и решений законодателей в представительских органах"
(Рикер [1982])
Большинство общественных распределенных решений (таких, как налоги и общественные расходы) принимаются на основе голосования. Выборы также используются для пополнения многих общественных заведений. Здесь мы имеем важные примеры чистых общественных продуктов (например, все граждане данного города без каких-либо исключений принимают участие в "потреблении" своего мэра), которые выбираются на основе голосования и без побочных платежей.
Начиная с политической философии Просветительского, выбор правил голосования был главной этической проблемой, повъъязаной с дополнениями, которые далеко идут, для функционирования большинства политических институтов. Дебаты о справедливости разнообразных методов голосования начались с исследований где Борда [1781] и Кондорсе [1785]. В 1952 году Ерроу предложил формальную модель, что в течение трех десятилетий анализировалась в многочисленных работах математической ориентации по так называемом коллективном выборе.
Формально правило голосование решает задачу коллективного принятия решения, у которой несколько индивидуальных агентов (избирателей) должны совместно выбрать один из нескольких результатов (также называемых кандидатами), относительно которых их мысли расходятся. Будем допускать, что конечное множественное число N избирателей должно избрать одного кандидата из конечного множественного числа А. Для простоту допустим, что индивидуальные мысли (или преимущества) не допускают случаи безразличия. Каждое такое преимущество является произвольным линейным порядком на А.
Реклама

Правило голосование выбирает кандидата на основе поставленных в известность порядковых преимуществ и только на основе этих преимуществ. В этом существенное отличие от моделей, в которых деньги и другие продукты позволяли осуществлять произвольно малые компенсации для агентов. Голосование не допускает уступки между двумя кандидатами иначе, чем за счет возможного избрания третьего кандидата.
Если кандидатов только два, то обычное правило голосования большинством голосов бесспорно является наиболее справедливым методом. Этот принцип большинства - исходный пункт процесса демократического принятия решений. Он был ясно сформулирован два столетия потому, а его основа является намного древнее. Аксиоматическая формализация принципа большинства предложена Мэем.
Рассмотрению методов голосования и воплощению в программу одного из них и посвященная дана курсовая работа. Будет проведена сравнительная характеристика разных методов голосования, и с помощью контрольного примера продемонстрированная робота одного из них.
1.
Содержательная постановка задачи
Задание, которое относится передо мной в данной курсовой работе, – обеспечить процесс выборов, то есть конечное множественное число N избирателей должно избрать одного кандидата из конечного множественного числа А. Обязательным условием есть избрание единственного кандидата. Для простоты допустим, что индивидуальные мысли (или преимущества) не допускают случаи безразличия. Каждая такое преимущество есть произвольным линейным порядом на А (то есть полное транзитивное и асимметричное бинарное отношение). Это предположение не приводит к существенным потерям всеобщности.
Формально правило голосование решает задачу коллективного принятия решения, у которой несколько индивидуальных агентов (избирателей) должны совместно выбрать один из нескольких результатов (также званых кандидатами), относительно которых их мысли расходятся.
Правило голосования являет собой систематическое решение, которое во всей полноте опирается по индивидуальным мнениям. Обозначим через L(А) множественное число линейных порядков на А, тогда правило голосование является отображением L(А) N в А. То, что правило голосования может быть определено для любой мыслимой конфигурации преимуществ, выражает фундаментальный принцип свободы мыслей: каждый избиратель имеет право ранжировать кандидатов любым образом. Однако в некоторых моделях голосования, которые содержат экономические переменные или неопределенные результаты, можно допускать, что преимущества избирателей удовлетворяют некоторому общему условию. Это особенно удобно при стратегическом анализе голосования и при агрегации преимуществ.
Реклама

Правило голосования выбирает кандидата на основе поставленных в известность порядковых преимуществ и только на основе этих преимуществ. В этом существенное отличие от моделей, в которых деньги и другие продукты позволяли осуществлять произвольно малые компенсации для агентов. Голосование не допускает уступку между двумя кандидатами иначе, чем за счет возможного избрания третьего кандидата.
Пусть дано как контрольный пример следующий профиль для 9 избирателей и 5-ти кандидатов:
| 1 |
4 |
1 |
3 |
a
b
c
d
e
|
c
d
b
e
a
|
e
a
d
b
c
|
e
a
b
d
c
|
В каждом столбце кандидаты расположенные в порядке уменьшения их значимости для каждой группы избирателей. То есть, для первого столбца (группы избирателей, которая состоит из одного человека) можно определить преимущества следующим образом: группа избирателей, которая состоит из одного лица, считает кандидата а наилучшим. На втором месте они ставят кандидата b, на третьем месте c и так далее аналогично кандидаты ранжированы в каждой группе.
Задание: определить единственного победителя выборов.
Существуют много способов определения победителя. Они будут описаны и соответствующим образом сравнены в следующих разделах.
Отметим сейчас, что дана курсовая работа посвященная рассмотрению и воплощению в программу метода Копленда и сравнению полученного результата с результатом за методом Борда.
Определим правило Копленда.
Сравним кандидата а
с любым другим кандидатом x.
Начислим ему +1
, если для большинства а лучше за x, -1,
если для большинства x
лучше за а
, и x
, x
¹a
, получаем оценку Копленда для а
. Избираем кандидат, названный победителем за Коплендом, с наивысшей такой оценкой.
В данном правиле не указано, что делать в том случае, когда найдутся два или больше кандидаты с одинаковой оценкой Копленда. Допустимо, что изберется тот кандидат, имя и фамилия которого стоит ближайшее по списку. Это предположение нарушает правило нейтральности, но, как будет доказано в следующих разделах, каждое правило голосования Копленда является наиболее наглядным и легким для компьютерной реализации.
Правило Борда
: каждый избиратель сообщает свои преимущества, ранжируя p кандидатов от наилучшего к наихудшему (безразличие запрещается). Кандидат не получает очки за последнее место, получает одно очко за предпоследнее место и так далее, получает p-1 очков за первое место. Побеждает кандидат с наибольшей суммой очков. Он называется победителем по Борду. Здесь так же не указывается, что делать при равенстве очков, то есть также может нарушаться условие нейтральности.
Охарактеризуем выше поставленную задачу.
Ее критерием качества является максимизация оценки Копленда (Борда).
Ограничениями выступают преимущества избирателей и их ранжирования кандидатов. Как будет указано дальше, фактически нужно налагать также ограничение и на количество избирателей и количество кандидатов. Однако это ограничение не является существенным, так как всегда при голосовании можно провести деление на округа.
За уровнем сложности это есть задача Р-типа. Время решения данной задачи составляет t0
=a0
+a1
x+… +an
xn
і зависит от количества групп избирателей и количества кандидатов.
Нахождения победителя по правилам Копленда и Борда являются самыми простыми за своей структурой, оптимальные по Парето, анонимные, нейтральные (если не указывать, что делать при равенстве очков). Кроме того, правило Борда также удовлетворяет аксиоме участия и пополнения (они будут рассмотрены в следующем разделе).
Оптимальность по Парето:
Если кандидат а для всех лучший от кандидата b, то b не может быть избран.
Анонимность:
Имена избирателей не имеют значения – если два избирателя поменяются голосами, то результат выборов не изменится.
Нейтральность:
Имена кандидатов не имеют значения. Если мы поменяем местами кандидатов а и b в преимуществе каждого избирателя, то результат голосования изменится соответственно (если раньше выбирался а, то теперь будет выбираться b и наоборот; если выбирался некоторый х, отличающийся от но и b, то он же и будет избран).
Монотонность:
Допустимо, что а выбирается (среди победителей) при данном профиле и профиль изменяется только так, что положение а улучшается, а относительное сравнение пары любых других кандидатов для любого избирателя остается неизменным. Тогда а как и раньше будет избран (опять среди победителей) для нового профиля.
2.
Формальная постановка задачи
Приведем еще раз задачу данной курсовой работы: используя профиль преимуществ избирателей, определить единственного победителя из множественного числа заданных. Должна существовать возможность проверки корректности задания профиля. Ограничениями на задачу является отсутствие безразличия и ранжировки кандидатов в строгом порядке. Опишем методы голосования, которые могут использоваться для решения данной задачи и наведем ряд основных определений и теорем.
Правило относительного большинства.
Каждый избиратель отдает свои голос наилучшему для себя кандидату. Избирается кандидат, упомянутый в наибольшем количестве бюллетеней. Это правило может противоречить мнению большинства (см. 1, пример 9.1).
Определение 2.1. Правило Борда.
Каждый избиратель сообщает свои преимущества, ранжируя р кандидатов от лучшего к хуже (безразличие запрещается). Кандидат не получает очков за последнее место, получает одно очко за предпоследнее и так далее, получает р-1 очков за первое место. Побеждает кандидат с наибольшей суммой очков. Он называется победителем по Борду.
Мы не уточняем, что делать при равенстве очков.
Определение 2.2.
Для заданного профиля преимуществ победителем по Кондорсу называется кандидат а, что побеждает любого другого кандидата при парном сравнении по правилу большинства:
для всякого b
¹
а
избирателей, которые считают а лучшим за b, больше, чем тех, кто считает, что b лучшим за а.
Зажиточное по Кондорсу правило выбирает победителя по Кондорсу, если такой существует.
Отсутствие победителя по Кондорсу является знаменитым "парадоксом голосования". Как часто может наблюдаться парадокс голосования? В общем случае вероятность p
(p
, n
) того, что победителя по Кондорсу не существует при р
кандидатах и n
избирателях, растет по р
и растет по числу избирателей от n
к n+2
. Это может быть проверено на основе вычисления p
(п
, р)
для малых значений n
и р
, но в общем случае это утверждение остается недоказанным предположением.
Парадокс голосования становится почти достоверным событием, когда число кандидатов становится достаточно большим при фиксированном n
. Если число избирателей становится достаточно большим при фиксированном р
, то предельная вероятность p
(p
) может быть оценена по Фишберну [1984]:
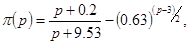
которая справедлива с точностью до половины процента при р
£50.
Определение 2.3. Правила голосования с подсчетом очков.
Фиксируем последовательность вещественных чисел, которая не спадает
s0
£s1
£…£sp-1
при s0
<sp-1
.
Избиратели ранжируют кандидатов, причем s0
очков дается за последнее место, s1
- за предпоследнее и так далее. Избирается кандидат с максимальной суммой очков.
Определение 2.4. Правило Копленда.
Сравним кандидата а
с любым другим кандидатом х
. Начислим ему +1
, если для большинства а
лучше за х, -1,
если для большинства х
лучше за а
, и 0 при равенстве. Суммируя общее количество очков по всем х
, х
¹а
,получаем оценку Копленда для а
. Избирается кандидат, названный победителем за Коплендом, с наивысшей из таких оценок.
Определение 2.5
. Правило Симпсона.
Рассмотрим кандидата а, любого другого кандидата х и обозначим через N(а,x) число избирателей, для которых а лучше за х. Оценкой Симпсона для а называется минимальное из чисел N(а,x) по всем х
, х
¹а
. Избирается кандидат, названный победителем по Симпсону, с наивысшей такой оценкой. Оба этих правила зажиточные по Кондорсу.
Оптимальность по Парето.
Если кандидат а для всех лучший от кандидата b, то b не может быть избранным.
Анонимность.
Имена избирателей не имеют значения: если два избирателя поменяются голосами, то результат выборов не изменится.
Нейтральность.
Имена кандидатов не имеют значения. Если мы поменяем местами кандидатов а
и b
в преимуществе каждого избирателя, то результат голосования изменится соответственно (если раньше выбирался а, то теперь будет выбираться b и наоборот; если выбирался некоторый х, отличающийся от а и b, то он же и будет выбран).
Правила Копленда и Симпсона оптимальные по Парето, анонимные и нейтральные, если мы рассматриваем их как отображения, которые ставят в соответствие каждому профилю преимуществ подмножество победителей. Анонимность и нейтральность очевидны. Проверить, что множественные числа победителей по Борду (Копленду, Симпсону) содержат только оптимальные по Парето результаты, достаточно просто. Да, оценка Симпсона кандидату, что доминируется по Парето, равняется нулю, а для оптимального по Парето кандидата она позитивна.
Монотонность
. Допустим, что а
выбирается (среди победителей) при данном профиле и профиль изменяется только так, что положение а
улучшается, а относительное сравнение пары любых других кандидатов для любого избирателя остается неизменным. Тогда а
как и раньше будет избран (опять среди победителей) для нового профиля.
Все правила подсчета очков, а также правила Копленда и Симпсона являются монотонными.
Относительное большинство с выбыванием.
В первом раунде каждый избиратель подает один голос за одного кандидата. Если кандидат набирает суровое большинство голосов, то он и избирается. В противном случае во втором туре проводится голосование по правилу большинства с двумя кандидатами, которые набрали наибольшее количество голосов в первом туре.
Сторонники этого метода подтверждают, что он почти так же простой, как и правило относительного большинства (избирателям не нужно сообщать полное ранжирование кандидатов), и исключает расточительные выборы. При обычном правиле относительного большинства, если я голосую за кандидата, который получает маленькую поддержку, то мой голос будет напрасным. Однако при выбывании у меня есть еще один шанс повлиять на результат.
Однако этот метод не является монотонным, как показывают такие два профиля с 17 избирателями:
| Профиль А |
Профиль B |
| 6 |
5 |
4 |
2 |
6 |
5 |
4 |
2 |
| a |
c |
b |
b |
a |
c |
b |
a |
| b |
a |
c |
a |
b |
a |
c |
b |
| c |
b |
a |
c |
c |
b |
a |
c |
При профиле А во второй тур проходять а
и b
и выигрывает а
(11 голосов против 6). Профиль В такой же за одним исключением. У двух избирателей преимущество b>a>с изменяется на преимущество а>b>с, то есть для них теперь а
лучше b
. Теперь во второй тур проходять а
и с
, причем выигрывает с
(9 голосов против 8). Таким образом, улучшение позиции кандидата а
приводит к его поражению!
Метод альтернативных голосов.
Исключим сначала тех, кто получил наименьшее количество голосов. Потом посчитаем голоса для кандидатов, которые остались, и опять исключим неудачников. Будем повторять эту операцию до тех пор, пока не останется один кандидат (или множественное число кандидатов с ровным числом голосов).
Здесь главное внимание уделяется потому, чтобы не потерять никаких голосов и каждому дать шанс поддержать кандидата, который нравится больше всего. В этом подходе повторно используются методы подсчета очков для исключения кандидатов-неудачников. К сожалению, любое правило, основанное на последовательном исключении по методу подсчета очков, должно нарушать свойство монотонности для некоторых профилей.
Пополнение (однозначные правила голосования)
. Две группы избирателей N1, N2,
что не пересекаются, имеют дело с тем же множественным числом А
кандидатов. Пусть избиратели N1
и N2
выбирают того же кандидата а
. Тогда избирателе N1
ÈN2
также изберут а
из А
.
Это свойство является очень обоснованным, когда единственный избирательный орган разбит на большое количество подмножеств, как в случае региональных ассамблей и подкомитетов.
Пополнение (отображение голосования).
Две группы избирателей N1, N2
, что не пересекаются, имеют дело с тем же множественным числом А
кандидатов. Пусть избиратели Ni
избирают подмножество Вi
з А
при i
=1,2. Если В1
и B2
пересекаются, то избирателе N1
ÈN2
изберут В1
ÇB2
как множественное число наилучших для себя результатов.
Теорема 2.1
(Янг [1975])
(а) Все отображения голосования, основанные на подсчете очков (подмножества кандидатов, которые выбирают, с наибольшим суммарным количеством очков), удовлетворяют аксиоме пополнения. Если при равенстве очков выбор проводится на основе фиксированного порядка на А, то соответствующие правила голосования также удовлетворяют аксиоме пополнения.
(b) Не существует зажиточного по Кондорсу правила голосования (или отображение голосования), которое бы удовлетворяло аксиоме пополнения.
Аксиома участия
. Пусть кандидат а выбирается из множественного числа А избирателями из N. Рассмотрим дальше избирателя и за N. Тогда избиратели из N
È{i
} должны избрать или а, или кандидата, что для агента I и строго лучше а.
Значит, что если дополнительный голос действительно изменяет результат выборов, то это может быть только на руку "ключевому" избирателю.
Теорема 2.2
(Мулен [1986с])
(a) Для всех правил голосования с подсчетом очков, когда при равенстве очков выбор осуществляется с помощью заданного порядка на А, выполняется аксиома участия.
(b) Если А состоит хотя бы из четырех кандидатов, то ни одно зажиточное по Кондорсу правило голосования не удовлетворяет аксиоме участия.
Непрерывность
. Пусть избиратели из N1 избирают кандидата а из A, а группа N2, которая не пересекается из N1, избирает другого кандидата b. Тогда существует достаточно большое число m дублей группы избирателей N1,
такое что комбинированная группа избирателей (mN1
)ÈN2
выберет а.
Теорема 2.3
(Янг [1975]).
Отображение голосования основано на методе подсчета очков (определение 2.3 без фиксации правила для случая равенства очков) тогда и только затем, когда оно удовлетворяет таким четырем свойствам:
анонимность, нейтральность
аксиома пополнения и непрерывность.

Голосование с последовательным исключением
.
Сначала по правилу большинства исключается или а, или b, потом по правилу большинства проводится сравнение победителя первого раунда и с и так далее. В случае равенства проигрывает нижний кандидат.
В этом процессе поправок пусть а - поправка, b - поправка к поправке, с - исходное предложение, d - status quo.
Этот метод удовлетворяет аксиоме по Кондорсу: если а - победитель по Кондорсу, то он выигрывает. В действительности возможность при сравнениях по правилу большинства справедливая в более широком содержании.
Возможность по Смиту. Если множественное число А кандидатов разбивается на два подмножества В1, B2, что не пересекаются, и каждый кандидат b1
ÎВ
1
выигрывает (за суровым большинством) у любого кандидата b2
ÎВ
2
, то должен быть избран результат из В1.
С другой стороны, голосование при последовательном исключении очевидно не является нейтральным. Порядок исключений, конечно, влияет на результат.
Правило равномерного исключения.
Сначала по правилу большинства выравниваются пары а из b и с из d. Победители встречаются в финале, где сравниваются по правилу большинства. В случае равенства выбирается кандидат, который идет раньше по алфавиту.
Это - опять зажиточный по Кондорсу метод. Более того, для избрания каждому кандидату х нужно победить в двух сравнениях по правилу большинства. Допустимо сначала, что равенства при сравнении с этими двумя кандидатами нет (х выигрывает для сурового большинства). Тогда х не может доминироваться по Парето некоторым кандидатом в, иначе b был бы победителем по Кондорсу. Следовательно, метод равномерного исключения выбирает оптимальный по Парето результат в случае, когда при бинарных выборах нет равенств. Однако если равенства возможны, то оптимум по Парето может нарушаться.
Бинарным деревом
на А есть такое конечное дерево, в котором каждой нефинальной вершине (включая начальную) отвечают ровно две следующие, а каждой финальной вершине (у которой нет следующих) приписан кандидат (элемент из A), причем каждый кандидат появляется по крайней мере в одной финальной вершине.
Среди бинарных деревьев самыми простыми являются те, в которых каждый кандидат приписан ровно одной вершине. Назовем их деревьями без повторных исключений.
Лемма 2.1
(а) Если А состоит из трех кандидатов, то дерево после последовательного исключения является единственным безповторним деревом. Соответствующее правило голосования оптимально за Парето (при нашем условии, что все сравнения по большинства суровые). (b) Если А состоит из четырех кандидатов, то есть только два безповторних деревья: последовательное исключение и ривнобижне исключение. Первое из них нарушает оптимум за Парето, а последнее - нет. (c) Если А содержит пять или больше кандидатов, то любое исключение по безповторному дереву приводит к избранию кандидата для некоторых профилей, во что доминируется по Парето.
Существует бинарное дерево, определенное для произвольного количества участников, что позволяет избежать обеих этих опасностей. Соответствующие последовательные исключения порождают оптимальное по Парето, анонимное и монотонное правило голосования. Это дерево называется деревом многоэтапного исключения.
Для каждого конкретного упорядочения кандидатов существует по одному такому дереву. Обозначим через Гp
(1,2,... ,р)
дерево, которое отвечает порядку A={1,2...,р}. Определим его индуктивно по размеру А
:
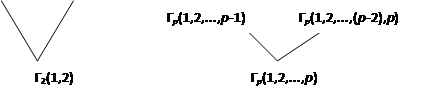
Да, для трех и четырех кандидатов получаем:
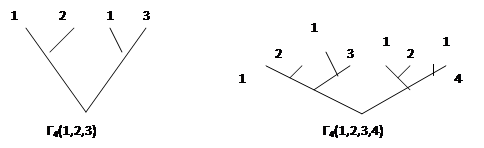
При р кандидатах образуются 2p-l финальные вершины; кандидат 1 приписанный 2p-2 финальным вершинам, а кандидат р только одной. Тем не меньше для избрания даже кандидату р нужно победить в р-1 дуэлях (хотя ему возможно придется по нескольку раз столкнуться с тем же оппонентом). Хотя дерево многоэтапного исключения большое, его решение (то есть вычисление кандидата, который выигрывает) может быть получено с помощью очень простого алгоритма.
Теорема 2.4
(Шепсл и Вейнгаст [1984]).
Заданы дерево многоэтапного исключения Гp
(1,2,... ,р
и профиль преимущества, которое отвечает мажоритарному турниру Т. Кандидат а* может быть найден по такому алгоритму:
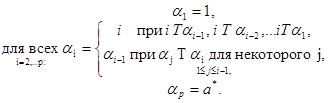 (12) (12)
Следствие теоремы 2.4.
Кандидат а, что выбирается по дереву многоэтапного исключения с турниром Т, удовлетворяет условию:
для любого b
ÎА
, b
¹а:
{аТb
} і/или
{для некоторого с
, аТс і сTb
}. (14)
В частности, а
оптимальный по Парето. Более того, дерево многоэтапного исключения порождает монотонный метод голосования.
Среди зажиточных по Кондорсу правил голосования мы обнаружили три метода, которые удовлетворяют основным требованиям оптимума по Парето, анонимности и монотонности: множественное число победителей по Копленду, множественное число победителей по Симпсону и дерево многоэтапного исключения. Первые два нейтральные, но могут выделять несколько победителей (дополнительное правило при равенстве очков нарушит нейтральность). Заметим, что победитель при многоэтапном исключении находится быстрее, поскольку алгоритм (12) в среднем нуждается в сравнении не больше половины от всех p(p-l) пар. В то же время для определения победителей по Копленду и Симпсону нужно провести весь турнир сравнений по правилу большинства.
3.
Математические методы решения
В предыдущем разделе были описанные методы подсчета глазков и основные требования к ним. Сравним эти методы. Как было отмечено, найлегшим среди них, но и наихудшим, есть правило относительного большинства. Можно убедиться, что в действительности оно противореччит мнению большинства. Поэтому оно не может быть выбрано для компьютерной реализации. Как Борда, так и Кондорсе заметили, что правило относительного большинства может приводить к избранию плохого кандидата, точнее такого кандидата, что в парном сравнении по правилу большинства проигрывает любому другому кандидату.
Для того, чтобы перебороть этот изъян, Кондорс и Борде предложили отказаться от правила относительного большинства, причем каждый из них предложил свое правило вместо данного. Кондорс предложил выбирать кандидата, который побеждает любого другого кандидата в парном сравнении, если такой победитель по Кондорсу существует. Борде предложил приписать очко каждому кандидату, который линейно растет в зависимости от его ранга в преимуществе избирателя. Потом он предложил избрать кандидата, который получил наибольшее суммарное количество очков у всех избирателей. Эти две идеи порождают два больше всего важных семейств правил голосования.
Результаты этих правил голосования могут сильно отличаться по свойствам. Одним из таких свойств есть аксиома монотонности. Правило голосование называется монотонным, если кандидат остается избранным при усилении его поддержки (то есть когда относительная позиция данного кандидата в чьих-то преимуществах улучшается, а относительные позиции других кандидатов не изменяются). Все методы подсчета глазков являются монотонными, но некоторые известные методы, что возникают из подсчета глазков, не являются такими. Примерами таких правил служит очень популярное правило относительного большинства с выбыванием и метод альтернативних голосов.
Есть две аксиомы, которые приводят к критике зажиточных по Кондорсе правил (поскольку данные правила нарушают эти аксиомы). С другой стороны, на этих аксиомах основана характеризация метода подсчета глазков. Эти аксиомы сравнивают кандидатов, избранных разнообразными группами избирателей. Они называются свойствами пополнения и участия. Пополнение значит, что если две группы избирателей, которые не пересекаются, (например, сенат и палата представителей) избирают того же кандидата а, то объединение этих двух избирательных органов подтвердит избрание а. Участие значит, что избиратель не может выиграть, воздерживаясь от голосования, в сравнении с возможностью принимать участие в голосовании и выразить свои преимущества. Любое зажиточное по Кондорсе правило нарушает обе этих аксиомы. В противовес этому правила подсчету очков характеризуются свойством пополнения (теорема Янга) и удовлетворяют аксиоме участия. Теорема Янга в настоящее время является самым существенным доказательством в поддержку методов подсчета очков, в частности системы очков Борда.
Зажиточные по Кондорсу правила голосования все же чрезвычайно популярны, в частности, благодаря простоте доведения парного сравнения по правилу большинства. Соответствующий класс зажиточных по Кондорсу методов основан на последовательных сравнениях по правилу большинства. Законопроект и многочисленные поправки к нему в конгрессе США голосуются именно таким способом. Известен метод последовательного исключения может нарушать условие оптимума по Парето. Другие методы, основанные на бинарных деревьях парных сравнений по правилу большинства, противоречат аксиоме монотонности. Наиболее простое правило, которое основано на последовательном сравнении и является оптимальным по Парето и монотонным, называется многоэтапным методом исключения. При использовании этого метода нужно меньше парных сравнений, чем в других, концептуально более простых методах, например в правиле Копленда. По последнему правилу избирается тот, кто выигрывает большинство парных дуэлей. Таким образом, голосование, основанное на последовательных парных сравнениях, может удовлетворять больше всего важным аксиоматическим требованиям, но только в том случае, если мы аккуратно выберем эту последовательность.
Правила Борда, относительного большинства и антибольшинства являют собой примеры правил голосования с подсчетом очков. Однако правило антибольшинства явно не монотонно, а правило относительного большинства – несправедливое.
Победитель Борда не может быть наихудших по Кондорсу, так как он является кандидатом, который имеет наивысший средний балл. По этому правилу всегда находятся оптимальный по Парето победитель или их множественное число. Примерами зажиточных по Кондорсу правил являются правила Копленда и Симпсона. Так же, как и правило Борда или любой другой метод подсчета очков, эти правила выбирают для каждого профиля подмножество победителей, которое может состоять из нескольких кандидатов, которые получили одинаковую оценку.
Как уже было отмечено, правила голосования должны быть монотонные, оптимальные по Парето, анонимные и нейтральные. Все правила голосования с подсчетом очков, кроме правила антибольшинства, оптимальны по Парето, монотонные, анонимные и нейтральные, если мы не указываем, что делать при равенстве очков. Кроме того, правила голосования должны удовлетворять аксиоме участия и пополнения. Метод Борда относится к этим правилам (это было показано в предыдущем разделе).
Правила Борда и Копленда, как отмечает Мулен, опираясь на практику, не очень части приводят к равенству очков, потому в этом ракурсе является наилучшими. Однако методы Кондорсе, к которым относится и правило Копленда, для некоторых профилей может не удовлетворять аксиоме участия.
Следующей группой правил являются правила, основанные на последовательном исключении за методом подсчета очков (относительное большинство с выбыванием, метод альтернативных голосов). Однако эти правила, как и любые другие методы, с выбыванием кандидатов нарушают свойство монотонности для некоторых профилей.
Метод ривнобижного исключения выбирает оптимальный за Парето результат в случае, когда при бинарных выборах нет ривностей. Однако если равенству возможные, то оптимум за Парето может нарушаться. Невзирая на выше перечисленные трудности, возможность за Кондорсе, широко известная в качестве демократического принципа, в то время как правило Борда "скрывает" настоящие симпатии избирателей за математической формулой. К зажиточным по Кондорсу правилам относят также следующие методы голосования:
а) голосование с последовательным исключением. При очевидных причинах это правило не является нейтральным и оптимальным по Парето, так как порядок исключений влияет на результат голосования. Определяя повестку дня, председатель фактически контролирует процесс выборов. Однако это правило достаточно широко используется Конгрессом США;
б) правило равномерного исключения. Оно порождает дерево без повторных исключений и требует проведения целого ряда мажоритарных турниров. Как было доказано в предыдущем разделе, бинарное дерево может дать оптимальное по Парето правило голосование только в более сложном случае, чем безповторне дерево. Также может нарушаться монотонность;
в) дерево многоэтапных исключений. Этот метод обеспечивает проведение наполовину меньшего количества мажоритарных турниров, чем метод Копленда. Оно имеет большой размер. Кандидатам, возможно, нужно принимать участие в дуэлях с тем же оппонентом по нескольку раз. Однако его алгоритм является достаточно простым. Дерево многоэтапного исключения порождает оптимальный за Парето и монотонный метод голосования. Всегда находится единственный победитель, а не множественное число. Однако этот метод порождает все трудности, которые связаны с использованием бинарных деревьев.
Таким образом, была проведена сравнительная характеристика всех методов голосования большинством голосов с исключением случаев безразличия и представления неправдивой информации.
Среди зажиточных по Кондорсу правил голосования мы обнаружили три метода, которые удовлетворяют основным требованиям оптимума по Парето, анонимности и монотонности: множественное число победителей по Копленду, множественное число победителей по Симпсону и дерево многоэтапного исключения. Среди методов подсчета очков наилучшим оказался метод определения победителя по Борду. Зажиточные по Кондорсу правила примененные на парном сравнении кандидатов по правилу относительного большинства. Для рядового избирателя они являются наиболее понятными.
Правило Борда удовлетворяет аксиоме участия и пополнения, но скрывает за математической формулой настоящие преимущества избирателей.
Для программной реализации выберем один из методов Копленда как самый простой и для сравнения определим победителя за Борда.
Приведем еще раз правила Копленда и Борда для того, чтобы перейти к формулировке алгоритма программы.
Правило Борда.
Каждый избиратель сообщает свои преимущества, ранжируя р кандидатов от лучшего к худшему (безразличность запрещается). Кандидат не получает очков за последнее место, получает одно очко за предпоследнее и так далее, получает р-1 очков за первое место. Побеждает кандидат с наибольшей суммой очков. Он называется победителем по Борду.
Правило Копленда.
Сравним кандидата а с любым другим кандидатом х. Начислим ему +1, если для большинства а лучше за х, -1, если для большинства х лучше за а, и 0 при равенстве. Суммируя общее количество очков по всем х
, х
¹
а
получаем оценку Копленда для а. Избирается кандидат, названный победителем по Копленду, с наивысшей из таких оценок.
Считаем, что входными данными задачи является уже сгруппированная информация: сформированные группы избирателей с одинаковыми в каждой группе рангами преимуществ. Однако допускается и занесение информации каждым избирателем отдельно.
4.
Описание алгоритма
В данном разделе наводятся алгоритмы для нахождения победителей выборов. Для определения победителей Борда и Копленда воспользуемся непосредственно приведенными выше правилами, то есть реализуем их программно. Сложность алгоритмов, описанных ниже, прямо пропорциональна количеству групп избирателей и количества кандидатов, что еще раз подтверждает принадлежность данной задачи к Р-типу.
4.1
Определение победителя Борда
Для нахождения оценок Борда кандидаты ранжируются, то есть за каждое место в шкале избирателей кандидат получает определенное количество баллов.
Далее эти баллы суммируются.
Введем следующие переменные.
Пусть М – количество кандидатов;
S – количество групп избирателей;
Nаme[M] – массив имен избирателей;
Rаng[1..M, 1..S] – профиль преимуществ;
Many[S] – количество избирателей в каждой группе;
Bord[M] – массив оценок кандидатов.
Рассматриваем отдельно каждую группу избирателей. Для этой группы кандидат получает оценку [количество избирателей many[i]]*([количество кандидатов M] – [текущее значение счетчика j]). Найденная оценка добавляется к предыдущей. Алгоритм продолжает работу до тех пор, пока не будут рассмотрены все группы избирателей (i=S).
По правилу Борда получаем следующий алгоритм для нахождения оценок Борда.
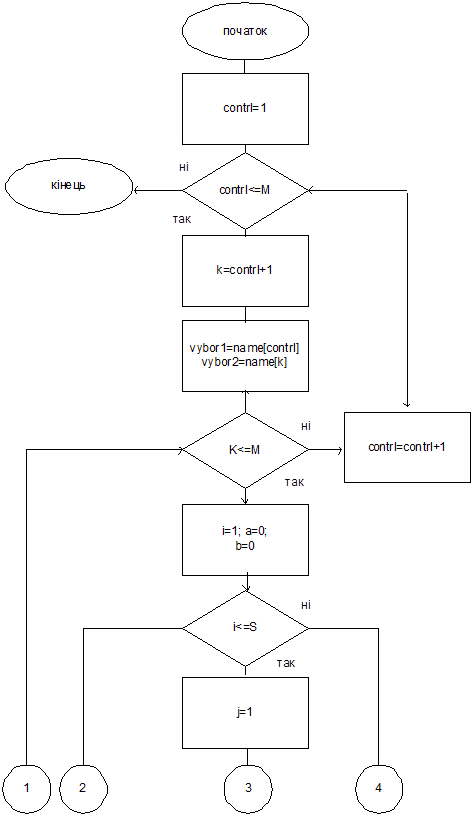
Рис. 4.1 Алгоритм нахождения оценок Борда.
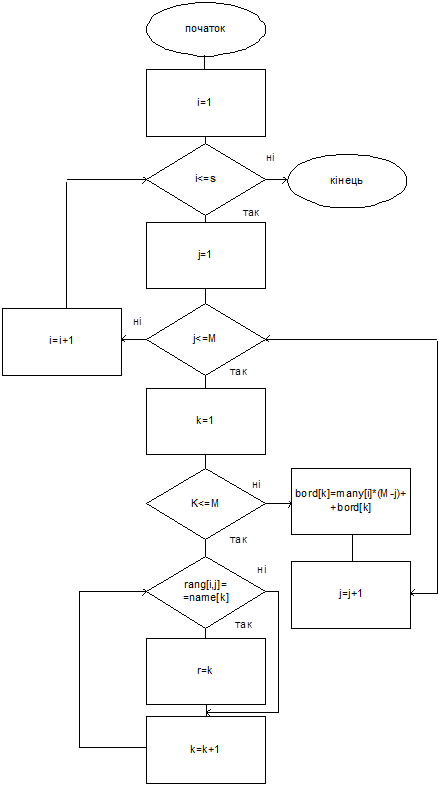
Рис. 4.2 Алгоритм нахождения оценок Копленда (начало)
4.2
Нахождение оценки Копленда
Для нахождения оценки Копленда кроме выше приведенных используем следующие переменные: Kopl[M] – массив оценок Копленда; Vybor1, vybor2 – вспомогательные переменные; используются для пересмотра имен кандидатов из массива имен name.
Сравнение проходит следующим образом.
Переменной vybor1 присваиваем значение имени первого кандидата из множественного числа имен name (contrl=1), а vybor2 – следующее (k=contrl+1). Если vybor1 находится выше, чем vybor2, в преимуществах избирателей всех групп, то к оценке Копленда (kopl[contrl]) кандидата vybor1 добавляется глазок, а vybor2 (kopl[k]) – отнимается и наоборот. Дальше переменной vybor2 присваивается следующее значение из массива имен (k=k+1), и процедура сравнения опять повторяется. Цикл продолжается до тех пор, пока не исчерпаются имена в списке кандидатов.
После этого переменной vybor1 присваивается второе имя из списка кандидатов (contrl=contrl+1), а vybor2 – третья. Опять проходит цикл по переменной vybor2. Цикл по переменной vybor1 заканчивается тогда, когда будут пересмотрены все кандидаты.
Получаем следующий алгоритм нахождения оценки Копленда.
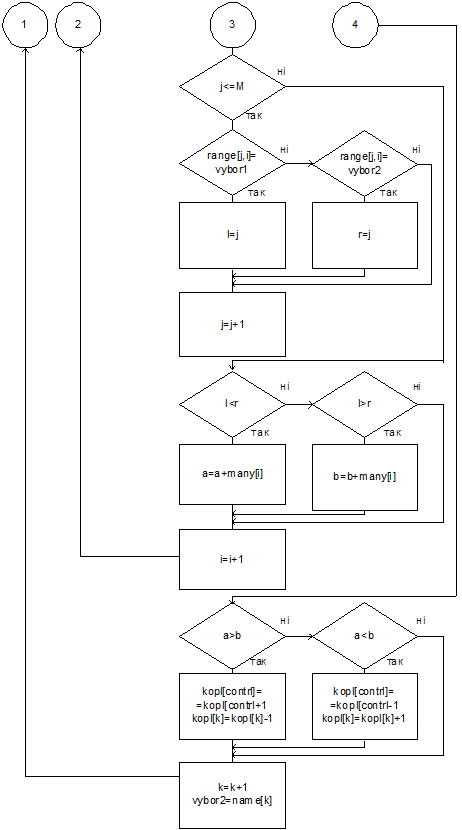
Рис. 4.3 Алгоритм нахождения оценок Копленда (конец)
4.3
Алгоритм определения победителя за правилами Борда или Копленда
Как можно было увидеть, победителем по Борду (Копленду) является кандидат с наивысшей суммой очков. Поэтому процесс его определения является одинаковым для обоих случаев, и я его объединила одним алгоритмом. Как известно, правила Копленда и Борда порождают множественное число решений. Для нахождения победителя используем следующие переменные: K – количество победителей; Max – оценка победителей; Hl[M] – массив номеров победителей.
Сначала массив номеров победителей заполняем нулями.
Массивы оценок Копленда и Борда (kopl и bord) заменим формальным массивом v[M].
После того, как мы нашли оценки для кандидатов (массивы kopl и bord), среди них ищем максимальную (max). Дальше отбираем кандидатов, оценка которых равняется max (их номера из массива name заносятся в массив hl), и считаем количество победителей (k).
Пересматриваем заполненный массив hl. Если в нем только первое значение отличающееся от нуля, то значит, что мы нашли единственного победителя, и, следовательно, сохранили условие нейтральности.
В другом случае просматриваем те значения имен кандидатов (массив name), номера которых встречаются в массиве hl. Отобраны имена кандидатов упорядочиваем по списку. Победителем становится тот, имя которого находится первым в данном списке.
В данном случае условие нейтральности не сохраняется.
Мы получили следующий алгоритм.
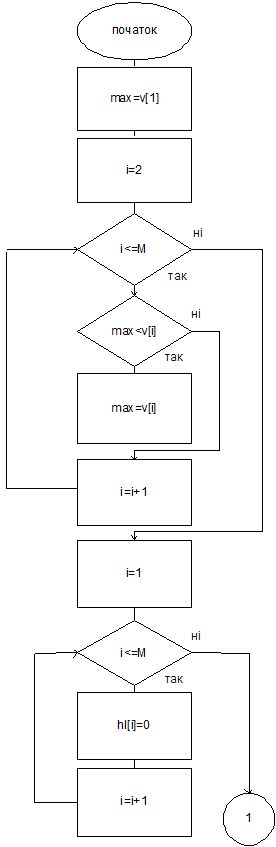
Рис. 4.4 Алгоритм определения победителя (начало).
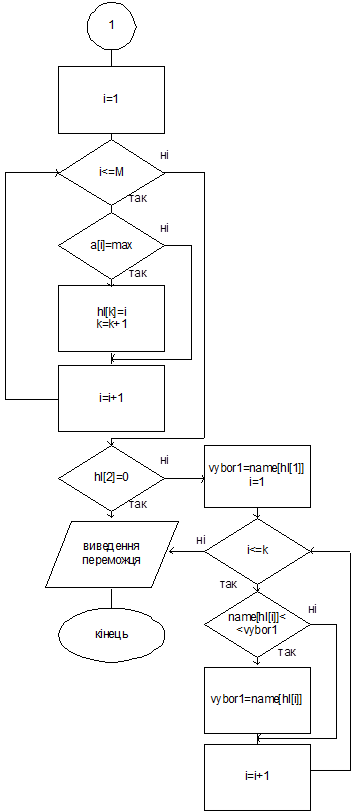
Рис. 4.5. Алгоритм определения победителя (конец).
5.
Описание программы
5.1
Выбор технологии программирования
Наиболее распространенными парадигмами программирования, которые к тому же могут быть использованы в данной курсовой работе, являются парадигмы процедурного и объектно-ориентированного программирования.
Парадигма процедурного программирования больше всего широко распространена среди существующих словно программирование (например, Си и Паскаль). Здесь явно выделяют два вида разнообразных сущностей:
1) процедуры, которые исполняют активную роль, то есть представляются тем, которое задает поведение (функционирование) программы;
2) данные, что исполняют пассивную роль, то есть представляют тем, которое прорабатывается средством, продиктованным процедурами. Возможность составлять процедуры из команд (операторов) и вызывать их является ключом данной парадигмы. Особенностью этой парадигмы являются "боковые эффекты", которые возникают в тех случаях, когда разнообразные процедуры, которые используют общие данные, независимо их изменяют.
В процедурной парадигме активная роль в организации поведения уделяется процедурам, а не данным; причем процедура активизируется вызовом. Подобные средства задания поведения удобны для описаний детерминированной последовательности действий или одного процесса, или нескольких, но строго взаимозависимых процессов. При использовании программирования, ориентированного на данные, активную роль играют данные, а не процедуры. Здесь со структурами активных данных связывают некоторые действия (процедуры), которые активизируются тогда, когда осуществляется доступ к этим данным. Некоторые специалисты называют это средство активации действий "демонами". Программирование, ориентированное на данные, позволяет организовать поведение мало зависимых процессов, что тяжело реализовать в процедурной парадигме. Имела зависимость процессов значит, что они могут рассматриваться и программироваться отдельно. Однако при использовании парадигмы, управляемой данными, эти независимо запрограммированные процессы могут взаимодействовать между собой без их изменения (то есть без перепрограммирования). Парадигма объектного программирования в отличие от процедурной парадигмы не разделяет программу на процедуры и данные. Здесь программа организуется вокруг сущностей, названных объектами, что включают локальные процедуры (методы) и локальные данные (переменные). Поведение (функционирование) в этой парадигме организуется путем пересылки сообщений между объектами. Объъект, получив сообщение, осуществляет его локальную интепретацию, базируясь на локальных процедурах и данных. Такой подход позволяет описывать сложные системы наиболее естественным путем. Особенно он удобен для интегрированных IC. Объектно-ориентированное программирование (ООП) базируется на абстракциях данных. В основе этого метода лежит представление предметной области в виде совокупности объектов, которые взаимодействуют между собой через передачу сообщений. Модель абстракции данных заключается в инкапсуляции данных и операций над ними в отдельный классовый тип. Доступ к данным возможная лишь с помощью инкапсулированных операций. Классовый тип является автономно завершенным и позволяет полное или частичное наследование для других классов. ООП концентрируется на цели задачи, для которой разрабатывается программа. Задача строится как совокупность объектов, которые взаимодействуют между собой с помощью сообщений. Элементы программы разрабатываются в соответствии с объектами в описании задачи. Суть ООП заключается в определении наиболее удачных объектовых типов. Объектовый тип служит модулем, который может быть использованным для решения других подобных задач. Такой подход не нуждается в специальной вычислительной технике, но существенно отличается характером мышления исполнителей в сравнении с процедурными языками программирования.
Через очевидную простоту алгоритма для реализации задачи лучше всего выбрать процедурную парадигму программирования и языка Паскаль или Си. Конечно, для написания красивого интерфейса можно взять объектно-ориентированные языки C Builder или Delphi. Однако, как можно было увидеть из рассмотрения алгоритма задачи, построение интерфейса сводилось бы к последовательному выведению окон. Еще одним аргументом в интересах словно Паскаль или Си есть размеры программы, которые бы при использовании C Builder или Delphi были намного большими.
Среди двух языков – Паскаль и Си, – я изберу Паскаль как более привычный для себя.
5.2
Структура программы
Структурно данную программу можно разделить на блоки.
Каждый блок может быть отнесен к одной из функциональных групп:
1. Построение интерфейса;
2. Реализация алгоритмов, представленных в разделе 4.
Следовательно, программа имеет следующую структуру:
Процедура victory – это реализация алгоритма определения победителя, описанного в предыдущем разделе. Во время вызова данной процедуры задается массив оценок Борда или Копленда, а также текст, для выведения результатов (им служат слова "Копленда" и"Борда"). В предыдущем разделе уже было обосновано, почему для определения победителя за разными правилами использован единственный алгоритм. Процедура help выводит список имен кандидатов в нижней строке экрана. Она введена для облегчения ввода информации пользователем.
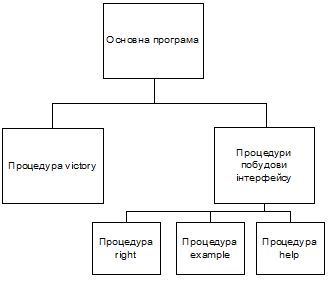
Рис. 5.1 Структура программы.
Процедура example содержит данные контрольного примера. Она введена для облегчения проверки правильности работы программы и носит демонстрационный характер.
Процедура right предназначена для проверки правильности вводу символа. Она используется при выборе внесения информации (демонстрация контрольного примера или самостоятельное внесение профиля) и выборе способа заноса данных (отдельными избирателями или работниками избирательного комитета).
Перейдем к рассмотрению основной программы.
Прежде всего в ней проходит вызов и взаимосвязь описанных выше процедур.
Процедуры построения интерфейса вызываются в начале работы программы. Они предназначенные для облегчения внесения данных.
Процедура victory определяет победителя и выводит результат голосования по определенному правилу. Потому ее вызов происходит напоследок основной программы.
Опишем переменные, которые используются в основной программе.
N: кол-во избирателей;
M: кол-во кандидатов;
s: кол-во групп;
rang: профиль преимуществ;
а,b: для определения оценки Копленда (используется в бинарных сравнениях);
kopl: массив оценок Копленда;
vybor1, vybor2: переменные внешних циклов при определении оценки Копленда;
bord: массив оценок Борда;
name: массив имен кандидатов;
к, и, j, l, r: вспомогательные переменные;
many: массив групп избирателей.
Опишем структуру программы.
Сначала программа просит внести всю нужную информацию. Пользователь должен указать количество избирателей и кандидатов и способ заноса информации (будет ли свои преимущества вносить каждый избиратель отдельно, будет ли это проводить комиссия, оперируя сгруппированными данными). Дальше идет внесение профиля преимуществ и проверка на его корректность. Профиль является некорректным, если в нем встречается имя лица, которое не является выше указанным кандидатом, или же имена кандидатов повторяются.
В программе используются алгоритмы правил Борда и Копленда, указанные в предыдущем разделе. Согласно полученных оценок определяется победитель с помощью процедуры victory, и проходит выведение результата.
Следует заметить, что полученные победители Копленда и Борда могут не совпадать, что еще раз свидетельствует о несовершенстве правил голосования большинством голосов. Результаты работы алгоритма будут показаны в соответствующем разделе.
Сложность программы (в данном случае понимается время, тратящее на выполнение), прямо пропорционально зависит от величины количества избирателей и кандидатов.
Так как данная программа носит более демонстрационный характер, то я ввела границу для количества избирателей и кандидатов для того, чтобы ограничить время выполнения – 200 и 50 соответственно. В общем оно не является существенным, так как всегда можно разбить избирательный округ на более малый с условием того, чтобы выполнялось данное ограничение.
5.3
Инструкция пользователю
Данная программа предназначенная для определения победителя выборов по правилам Копленда и Борда и сравнение полученных результатов.
В начале работы программы пользователь может выбрать, просматривать ли результаты решения контрольного примера, вносить ли собственные данные. В обоих случаях определяются победители за Коплендом и Борда.
Сначала работники избирательного органа вносят общую информацию: количество избирателей в данном округе то количество кандидатов. Дальше заносятся имена кандидатов и указывается способ заноса профилей преимуществ: каждым избирателем отдельно или работниками избирательного округа. В последнем случае информация сгруппирована (аналогично к контрольному примеру).
Внизу екрана выводятся имена всех кандидатов. Каждый избиратель (работник ли избирательного округа) вносит профиль преимуществ, располагая кандидатов в строго определенном порядке.
Для каждого избирателя не допускается случаев безразличия; кроме того, кандидаты должны быть строго ранджовани (то есть каждый из них занимает свое место в преимуществе избирателя, и на одном уровне не могут находиться два кандидата). Имена кандидатов, которые заносятся избирателями, повинны совпадать с именами, указанными в начале заполнения информации.
После заноса всех этих данных выдается результат работы программы.
Сначала выводится победитель Копленда и указывается, определен ли он с сохранением нейтральности. Для победителя указывается его оценка. В противном случае выводится множественное число победителей (кандидатов, сумма глазков которых равняется максимальной оценке).
Аналогично определяется победитель Борда.
Как будет показано в контрольном примере, оценки кандидатов, полученных по правилам Борда и Копленда, могут ранджуватись в противоположном порядке.
6.
Контрольный пример
Пусть дан следующий профиль для 9 избирателей и 5-ти кандидатов:
| 1 |
4 |
1 |
3 |
a
b
c
d
e
|
c
d
b
e
a
|
e
a
d
b
c
|
e
a
b
d
c
|
В каждом столбце кандидаты расположенные в порядке уменьшения их значимости для каждой группы избирателей. То есть, для первого столбца можно определить преимущества следующим образом: группа избирателей, которая состоит из одного лица, считает кандидата а наилучшим. На втором месте они ставят кандидата b, на третьем месте c и т.д.
Продемонстрируем решение контрольного примера по правилу Копленда. Определяем оценку Копленда.
Кандидат а является лучшим за b для 1+1+3 избирателей, а для 4-х избирателей кандидат b является лучшим за а. Определим такие преимущества для каждого кандидата, сравним его со всеми другими.
ab – 5
ac – 5
ad – 5
ae – 1
|
ba – 4
ca – 4
da – 4
ea – 8
|
bc – 5
bd – 4
de – 5
|
cb – 4
db – 5
eb – 4
|
cd – 5
ce – 5
|
dc – 4
ec – 4
|
de – 5 |
ed – 4 |
Определим оценку Копленда для каждого кандидата. Кандидат а является лучшим за b
(добавляем +1); он также является лучшим за c и d (добавляем два разы +1) и худшим за e
(добавляем –1). Следовательно, оценка Копленда для а
ровна 2.
Найдем оценку для других кандидатов.
a=+1+1+1-1=2
b=-1+1-1+1=0
c=-1-1+1+=0
d=-1+1-1+1=0
e=+1-1-1-1=-2
Среди полученных оценок определяем максимальную. Как видим, она равняется 2 и принадлежит кандидату а. Следовательно, а – победитель Копленда.
Если бы у нас получились два кандидата с максимальной оценкой, например b и f, мы бы избрали кандидата b, так как он расположен ближе за алфавитом.
Для этого же профиля найдем победителя Борда.
Следовательно, получаем такие оценки:
a=1*4+4*0+1*3+3*3=16
b=3*1+2*4+1*1+2*3=18
c=2*1+4*4+0+0=18
d=1*1+4*3+2*1+1*3=18
e=1*4+1*4+3*4+0=20
Победителем за Борда является кандидат е
.
Как видим, оценки Борда ранжируют кандидатов в порядке, противоположном до того, который получается по оценкам Копленда.
Выводы
Данная курсовая работа была посвящена обзору методов голосования большинством голосов. Была проведена сравнительная характеристика каждого из методов и из их множественного числа избраны наилучшие. К ним относятся:
1. зажиточные за Кондорсе правила Копленда и Симпсона, дерево многоэтапного исключения;
2. один из методов подсчета очков – правило Борда.
Все эти правила удовлетворяют условиям оптимума по Парето, монотонности и анонимности. Кроме того, правило Борда удовлетворяет также аксиоме участия и пополнения.
Для программной реализации были избраны методы Копленда и Борда.
Результаты работы программы продемонстрированы на контрольном примере.
Список литературы
1. Мулен Э. "Кооперативное принятие решений: Аксиомы и модели" – Москва, Мир, 1991.
2. Миркин Б. Проблема группового выбора. – Москва, Наука, 1974.
3. Льюс Р.Д., Райфа Х. Игры и решения. М.: ИЛ, 1961.
4. Антонов А. В. "Системный анализ", М.-2004г.
5. Ларичев О.И. Наука и искусство принятия решений. – М: Наука, 1979. – 200 с.
6. Макаров И.М. Теория выбора и принятия решений. – М.: Наука,1987. – 350 с.
7. Кузнецов А.В., Сакович В.А., Холод Н.И. "Высшая математика. Математическое программирование ", Минск, Вышейшая школа, 2001г.
8. Красс М.С., Чупрынов Б.П. "Основы математики и ее приложения в экономическом образовании", Издательство "Дело", Москва 2001г.
9. В.И. Ермаков "Общий курс высшей математики для экономистов", Москва, Инфра-М, 2000г.
10. Теория прогнозирования и принятия решений. М:1989. 160 стр.
Дополнения
Программа
uses wincrt;
label в, z;
type mas = string[6];
type ball =array[1..10] of shortint;
var N: byte; {кол-во избирателей}
M: byte; {кол-во кандидатов}
s: byte; {кол-во групп}
rang: array[1..10,1..100] of mas; {профильпреимуществ}
к,i,j,l,r,contrl: byte;
а,b: byte; {для проведения парных сравнений}
kopl: ball; {массив оценок Копленда}
vybor1, vybor2: mas;
bord: ball; {массивоценокБорда}
name: array[1..10] of mas; {массивименкандидатов}
many: array[1..100] of byte; {массивгруппизбирателей}
n1: array[1..10] of mas;
c: char;
{данные контрольного примера}
{---------------------------}
procedure example;
var и, j: byte;
begin
clrscr; M:=5; n:=9; s:=4;
name[1]:='a'; name[2]:='b'; name[3]:='c'; name[4]:='d'; name[5]:='e';
many[1]:=1; many[2]:=4; many[3]:=1; many[4]:=3;
rang[1,1]:='a'; rang[1,2]:='c'; rang[1,3]:='e'; rang[1,4]:='e';
rang[2,1]:='b'; rang[2,2]:='d'; rang[2,3]:='a'; rang[2,4]:='a';
rang[3,1]:='c'; rang[3,2]:='b'; rang[3,3]:='d'; rang[3,4]:='b';
rang[4,1]:='d'; rang[4,2]:='e'; rang[4,3]:='b'; rang[4,4]:='d';
rang[5,1]:='e'; rang[5,2]:='a'; rang[5,3]:='c'; rang[5,4]:='c';
gotoXY(15,1);
writeln; writeln('Число избирателей: ', N);
writeln('Число кандидатов: ', M);
writeln('Профильпреимуществ:');
for i:=1 to 40 do
write('-');
writeln; write('Число избирателей ');
gotoXY(19,7);
for i:=1 to s do
write(many[i] ' ');
writeln; gotoXY(19,9);
for i:=1 to M do
begin
for j:=1 to s do
write(rang[і,j] ' ');
gotoXY(19, 9+i);
end;
gotoXY(1,15);
end;
{---------------------------}
{проверяет правильность ввода варианта выбора} procedure right;
label l;
begin
l: readln(c);
if (c<>'0') and (c<>'1') then
begin
write('Повторите попытку: ');
goto l;
end;
end;
{---------------------------}
{выводит список имен кандидатов}
procedure help;
var x,y,i: byte;
begin
x:=WhereX;
y:=WhereY;
gotoXY(1,24);
write('Имена кандидатов: ');
for i:=1 to M do
if i<>M then write(name[i] ', ')
else write(name[i]);
gotoXY(x,y);
end;
{---------------------------}
{определениепобедителявыборов}
procedure victory(v: ball; s: string);
var max, t: shortint;
hl: array[1..10] of byte;
begin
{определение максимальной оценки}
help;
max:=v[1];
for i:=1 to M do
if max<v[i] then
max:=v[i];
t:=1;
{определение кандидатов с максимальной оценкой}
for i:=1 to M do
if (v[i]-max)=0 then
begin
hl[t]:=i;
t:=t+1;
end;
if (t-1)=1 then
begin
write('Победитель за ', s ' с сохранением нейтральности: ');
writeln(name[hl[1]]); writeln('Суммаочков - ', max);
end
else
begin
vybor1:=name[hl[1]];
for i:=2 to t-1 do
if name[hl[i]]<vybor1 then
vybor1:=name[hl[i]];
write('Победитель за ', s ' без сохранения нейтральности: ');
writeln(vybor1);
writeln('Суммаочков - ', max);
writeln('избранный из множественного числа наилучших:');
for i:=1 to t-1 do
writeln(name[hl[i]]);
end;
end;
{---------------------------}
{основная программа}
begin
gotoXY(21,1); writeln('Определение победителя выборов');
writeln; writeln('Запуск контрольного примера - 1; Самостоятельное внесение профиля 0');
right;
if c='1' then
begin
example;
help;
goto z;
end
else clrscr;
write('Введите количество кандидатов: ');
readln(M);
write('Введите количество избирателей: ');
readln(N);
writeln('Введите имена кандидатов');
for i:=1 to M do
begin
write('Кандидат ', и ': ');
readln(name[i]);
end;
writeln('Как будет осуществляться занос
информации?');
write('1- отдельными избирателями, 0- комитетом: ');
right;
if c='1' then
for i:=1 to N do
many[i]:=1;
clrscr; writeln('Введитепрофильпреимуществ');
s:=1; contrl:=0;
while contrl<>N do
begin
if c='1' then writeln('Избиратель ', s)
else writeln('Группа ', s);
for i:=1 to m do
n1[i]:='';
help;
for j:=1 to M do
begin
y:readln(vybor1);
{проверка на корректность введенного профиля}
r:=0; a:=0; b:=0;
n1[j]:=vybor1;
for l:=1 to M do
begin
if vybor1=name[l] then
begin
b:=1;
for a:=1 to M do
{такое имя уже было введено в данном профиле}
if (vybor1=n1[a]) and ((a-j)<>0) then r:=1;
end;
{имя введенного кандидата не совпадает с ни одним из списка}
if (vybor1<>name[l]) and (l=M) and
(b<>1) then r:=1;
end;
if r=1 then
begin
n1[j]:='';
writeln('Внимательно вводите имена кандидатов');
goto в;
end
else rang[j,s]:=vybor1; {профилькорректен}
end;
if c='0' then
begin
writeln('Количество избирателей в
группе ', s);
readln(many[s]);
contrl:=contrl+many[s];
end
else
contrl:=contrl+1;
s:=s+1;
clrscr;
end; {while}
{Определение оценок Копленда}
z: contrl:=1;
while contrl<=M do
begin
k:=contrl+1;
vybor1:=name[contrl]; vybor2:=name[k];
while k<=M do
begin
i:=1; a:=0; b:=0;
while i<=s do
begin
for j:=1 to M do
if rang[j,i]=vybor1 then l:=j
else
if rang[j,i]=vybor2 then r:=j;
if l<r then a:=a+many[i]
else
if l>r then b:=b+many[i];
i:=i+1;
end;
if a>b then
begin
kopl[contrl]:=kopl[contrl]+1;
kopl[k]:=kopl[k]-1;
end
else
if a<b then
begin
kopl[k]:=kopl[k]+1;
kopl[contrl]:=kopl[contrl]-1;
end;
k:=k+1;
vybor2:=name[k];
end; {while пок}
contrl:=contrl+1;
end; {whileпо contrl}
{определение оценок Борда}
for i:=1 to s do
for j:=1 to M do
begin
for k:=1 to M do
if rang[j,i]=name[k] then r:=k;
bord[r]:=many[i]*(M-j)+bord[r];
end;
victory(kopl, 'Коплендом');
writeln ('Нажмителюбуюклавишу
'); readkey; writeln;
victory(bord, 'Борда');
end.
Результаты работы программы
Самостоятельное внесение профиля.
Введите количество кандидатов: 5
Введите количество избирателей: 9
Введите имена кандидатов
Кандидат 1: а
Кандидат 2: b
Кандидат 3: c
Кандидат 4: d
Кандидат 5: е
Как будет осуществляться занос
информации?
1-отдельными избирателями, 0 –
комитетом: 0
Введите профиль преимуществ
Группа 1
a
b
c
d
e
Количество избирателей в группе 1: 1
Группа 2
c
d
b
e
a
Количество избирателей в группе 2: 4
Группа 3
e
a
d
b
c
Количество избирателей в группе 3: 1
Группа 4
e
a
b
d
c
Количество избирателей в группе 4: 3
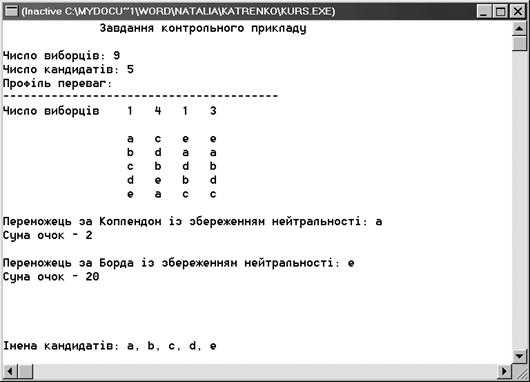
Победитель по Копленду с сохранением нейтральности – а
Сумма очков – 2
Победитель по Борду с сохранением нейтральности – е
Сумма очков – 20
Результаты работы программы
|