МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОУ ВПО Омский государственный технический университет
Кафедра «Экономика и организация труда»
Контрольная раБОтА
по дисциплине «Методы и модели в экономике»
Вариант 28
Выполнил:
студент гр. ЗУТ-217
Чупраков Д. А.
Проверила:
__________ Е. Н. Казанцева
«___» ___________ 2009 г.
Омск 2009
СОДЕРЖАНИЕ
Задача 1
Задача 2
Задача 3
Задача №1
1. Составить математическую модель задачи.
Сельскохозяйственное предприятие обязалось поставить в два магазина 25 и 35 т картофеля соответственно. Предприятие располагает тремя складами с запасами картофеля 15, 20 и 30 т соответственно. Расходы на поставку 1 т картофеля с каждого из складов в оба магазина даны в таблице.
| Магазины Склады |
№1 |
№2 |
| №1 |
20 руб. |
45 руб. |
| №2 |
30 руб. |
20 руб. |
| №3 |
40 руб. |
35 руб. |
Составить наиболее дешёвый план перевозок картофеля по каждому из технологических способов, чтобы получить максимум прибыли?
Решение
Введем переменные 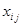 , представляющие собой количество товара, поставляемого из каждого i-го склада в каждый j-ый магазин. , представляющие собой количество товара, поставляемого из каждого i-го склада в каждый j-ый магазин.
Поскольку суммарные запасы 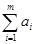 = 65 (т) и суммарные потребности = 65 (т) и суммарные потребности 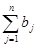 = 60 (т) не совпадают (т.е. мы имеем дело с открытой транспортной задачей), необходимо ввести фиктивный = 60 (т) не совпадают (т.е. мы имеем дело с открытой транспортной задачей), необходимо ввести фиктивный 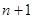 пункт потребления пункт потребления 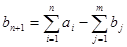 . Тогда транспортная матрица будет иметь следующий вид (табл.1). . Тогда транспортная матрица будет иметь следующий вид (табл.1).
Таблица 1- Общий вид транспортной матрицы
| Пунктыпроизводства, i |
Пункты потребления, j |
Объем производства |
| 1 |
2 |
3 |
| 1 |
20 |
45 |
0 |
15 |
| 2 |
30 |
20 |
0 |
20 |
| 3 |
40 |
35 |
0 |
30 |
| Объем потребления (спрос) |
25 |
35 |
5 |
65 |
Зададим целевую функцию и ограничения, т.е. построим математическую модель транспортной задачи.
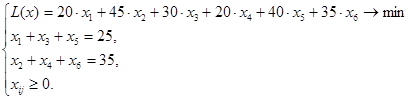
Найдем опорный план транспортной задачи методом северо-западного угла (табл. 2).
Таблица 2 – Транспортная матрица с опорным планом северо-западного угла
Пункты
производства, i
|
Пункты потребления, j |
Объем производства |
| 1 |
2 |
3 |
| 1 |
20
15
|
45
-
|
0
-
|
15/0 |
| 2 |
30
10
|
20
10
|
0
-
|
20/10/0 |
| 3 |
40
-
|
35
25
|
0
5
|
30/5/0 |
| Объем потребления |
25/10/0 |
35/25/0 |
5/0 |
65 |
Опорный план 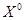 , найденный методом северо-западного угла имеет вид: , найденный методом северо-западного угла имеет вид:
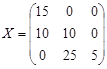 (т) или (т) или 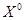 = (15; 0; 0; 10; 10; 0; 0;25;5). = (15; 0; 0; 10; 10; 0; 0;25;5).
Целевая функция, выражающая общие затраты на перевозку, будет иметь вид: 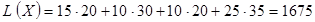 (руб.). (руб.).
Итерация 1.
Шаг 1.1. Вычисление потенциалов
20
15
|
45
-
|
0
-
|
u1
=0 |
30
10
|
20
10
|
0
-
|
u2
=-10 |
 |
40
-
|
35
25
|
0
5
|
u3
=-25 |
| v1
=20 |
v2
=10 |
v3
=-25 |
Система для плана 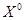 имеет вид: имеет вид: 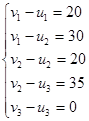
Полагая u1
=0, находим значения всех потенциалов: v1
=20, v2
=10, u2
=-10, v3
= - 25, u3
= - 25, т.е. (0; - 10; -25; 20; 10; -25).
Шаг 1.2. Проверка на оптимальность. Составляем таблицу оценок 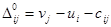 . .
| 0 |
-35 |
-25 |
u1
=0 |
| 0 |
0 |
-15 |
u2
=-10 |
| ∆1
= |
10 |
-10 |
-5 |
u3
=-25 |
| v1
=20 |
v2
=10 |
v3
=-25 |
Так как имеются  >0, то переходим к шагу 3. >0, то переходим к шагу 3.
Шаг 1.3. Составление нового плана перевозок.  соответствует клетка К31
. соответствует клетка К31
.
-30
  10 10
|
+20
 10 10
|
| ∆1
= |
 +40 +40
-
|
-35
25
|
Θ =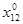 = 10. Составим новый план перевозки. = 10. Составим новый план перевозки.
Итерация 2.
Шаг 2.1. Вычисление потенциалов
Реклама

20
15
|
45
-
|
0
-
|
u1
=0 |
30
-
|
20
20
|
0
-
|
u2
=-5 |
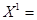 |
40
10
|
35
15
|
0
5
|
u3
=-20 |
| v1
=20 |
v2
=15 |
v3
=-20 |
Система для плана 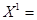 имеет вид: имеет вид: 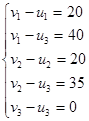
Полагая u1
=0, находим значения всех потенциалов: (0; -5; -20; 20; 15; -20).
Шаг 2.2. Проверка на оптимальность. Составляем таблицу оценок 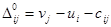 . .
| 0 |
-35 |
-20 |
u1
=0 |
| -5 |
0 |
-15 |
u2
=-5 |
| ∆1
= |
0 |
0 |
0 |
u3
=-20 |
| v1
=20 |
v2
=15 |
v3
=-20 |
Так как все оценки 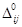 ≤0, следовательно, план ≤0, следовательно, план  - оптимальный. - оптимальный.
Х оптим
= (0; -5; -20; 20; 15; -20), следовательно, оптимальное значение целевой функции: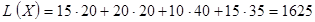 (руб.). (руб.).
Ответ: Х оптим
= (0; -5; -20; 20; 15; -20), L(X) = 1625 руб.
Задача №2
2. Решить графически задачу: найти экстремумы функции  , если , если 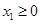 , , 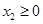 . .
Решить симплекс-методом
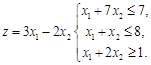
РЕШЕНИЕ
а) Решим задачу графически при
z = 3x1
– 2x2
→ max
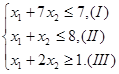
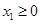 , , 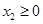 . .
Построим на плоскости прямые ограничений, вычислив координаты точек пересечения этих прямых с осями координат (рис.1).
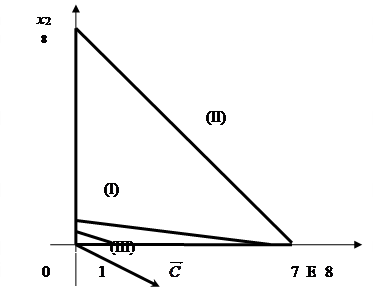 Рис.1. Графическое решение задачи при z = 3x1
– 2x2
→ max
Строим вектор 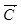 из точки (0;0) в точку (3; -2). Точка Е (7;0) – это последняя вершина многоугольника допустимых решений, через которую проходит линия уровня, двигаясь по направлению вектора из точки (0;0) в точку (3; -2). Точка Е (7;0) – это последняя вершина многоугольника допустимых решений, через которую проходит линия уровня, двигаясь по направлению вектора 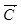 . Поэтому Е – это точка максимума целевой функции. Тогда максимальное значение функции равно: . Поэтому Е – это точка максимума целевой функции. Тогда максимальное значение функции равно:
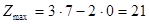 . .
б) Решим задачу графически при
z = 3x1
– 2x2
→ min
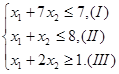
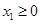 , , 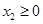 . .
Построим на плоскости прямые ограничений, вычислив координаты точек пересечения этих прямых с осями координат (рис.2).
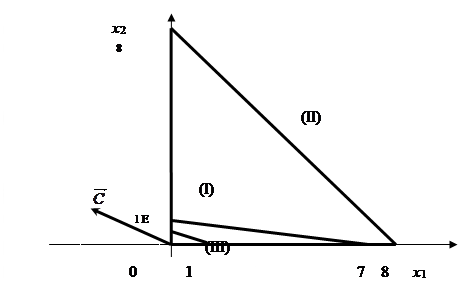 Рис.2. Графическое решение задачи при z = 3x1
– 2x2
→ min
Строим вектор  из точки (0;0) в точку (-3; 2). Точка Е (0;1) – это последняя вершина многоугольника допустимых решений, через которую проходит линия уровня, двигаясь по направлению вектора из точки (0;0) в точку (-3; 2). Точка Е (0;1) – это последняя вершина многоугольника допустимых решений, через которую проходит линия уровня, двигаясь по направлению вектора  . Поэтому Е – это точка минимума целевой функции. Тогда минимальное значение функции равно: . Поэтому Е – это точка минимума целевой функции. Тогда минимальное значение функции равно:
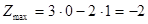 . .
Ответ: а) Функция z = 3x1
– 2x2
→ max и равна 21 в точке (7;0).
б) Функция z = 3x1
– 2x2
→ min и равна - 2 в точке (0;1).
Задача №3
Решить методом потенциалов транспортную задачу, где 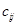 – цена перевозки единицы груза из пункта – цена перевозки единицы груза из пункта 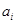 в пункт в пункт 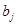 . .
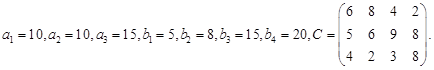
Решение
Поскольку суммарные запасы 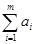 = 35 (ед. груза) и суммарные потребности = 35 (ед. груза) и суммарные потребности 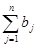 = 48 (ед. груза) не совпадают (т.е. мы имеем дело с открытой транспортной задачей), необходимо ввести фиктивный = 48 (ед. груза) не совпадают (т.е. мы имеем дело с открытой транспортной задачей), необходимо ввести фиктивный 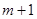 пункт производства пункт производства 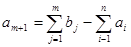 . Тогда транспортная матрица будет иметь следующий вид (табл.1). . Тогда транспортная матрица будет иметь следующий вид (табл.1).
Таблица 1- Общий вид транспортной матрицы
| Пунктыпроизводства, i |
Пункты потребления, j |
Объем производства |
| 1 |
2 |
3 |
4 |
| 1 |
6 |
8 |
4 |
2 |
10 |
| 2 |
5 |
6 |
9 |
8 |
10 |
| 3 |
4 |
2 |
3 |
8 |
15 |
| 4 |
0 |
0 |
0 |
0 |
13 |
| Объем потребления (спрос) |
5 |
8 |
15 |
20 |
48 |
Найдем опорный план транспортной задачи методом северо-западного угла (табл. 2).
Таблица 2 – Транспортная матрица с опорным планом северо-западного угла
Пункты
производства, i
|
Пункты потребления, j |
Объем производства |
| 1 |
2 |
3 |
4 |
| 1 |
6
5
|
8
5
|
4
-
|
2
-
|
10/5/0 |
| 2 |
5
-
|
6
3
|
9
7
|
8
-
|
10/7/0 |
| 3 |
4
-
|
2
-
|
3
8
|
8
7
|
15/7/0 |
| 4 |
0
-
|
0
-
|
0
-
|
0
13
|
13/0 |
| Объем потребления |
5/0 |
8/3/0 |
15/8/0 |
20/13/0 |
48 |
Опорный план 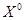 , найденный методом северо-западного угла имеет вид: , найденный методом северо-западного угла имеет вид:
Реклама

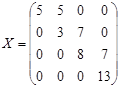 (ед. груза) или (ед. груза) или 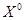 = (5; 5; 0; 0; 0; 3; 7;0;0;0;8;7;0;0;0;13). = (5; 5; 0; 0; 0; 3; 7;0;0;0;8;7;0;0;0;13).
Целевая функция, выражающая общие затраты на перевозку, будет иметь вид: 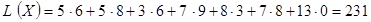 (ден. ед.). (ден. ед.).
Итерация 1.
Шаг 1.1. Вычисление потенциалов
6
5
|
8
5
|
4
-
|
2
-
|
u1
=0 |
5
-
|
6
3
|
9
7
|
8
-
|
u2
=2 |
 |
4
-
|
2
-
|
3
8
|
8
7
|
u3
=8 |
0
-
|
0
-
|
0
-
|
0
13
|
u4
=16 |
| v1
=6 |
v2
=8 |
v3
=11 |
v4
=16 |
Система для плана  имеет вид: имеет вид: 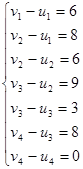
Полагая u1
=0, находим значения всех потенциалов: v1
=6, v2
=8, u2
=2,v3
=11, v4
=16, u3
=8, u4
=16, т.е. (0; 2; 8; 16; 6; 8; 11; 16).
Шаг 1.2. Проверка на оптимальность. Составляем таблицу оценок 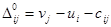 . .
| 0 |
0 |
7 |
14 |
u1
=0 |
| -1 |
0 |
0 |
6 |
u2
=2 |
| ∆1
= |
-6 |
-2 |
0 |
0 |
u3
=8 |
| -10 |
-8 |
-5 |
0 |
u4
=16 |
| v1
=6 |
v2
=8 |
v3
=11 |
v4
=16 |
Так как имеются 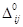 >0, то переходим к шагу 3. >0, то переходим к шагу 3.
Шаг 1.3. Составление нового плана перевозок. 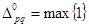 соответствует клетка К14
. соответствует клетка К14
.
- 8
  5 5
|
4
-
|
+2
 - -
|
+6
 3 3
|
- 9
 7 7
|
8
-
|
| ∆1
= |
2
-
|
+3
 8 8
|
- 8
7
|
0
-
|
0
-
|
0
13
|
Θ =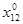 = 5. Составим новый план перевозки. = 5. Составим новый план перевозки.
Итерация 2.
Шаг 2.1. Вычисление потенциалов
6
5
|
8
-
|
4
-
|
2
5
|
u1
=0 |
5
-
|
6
8
|
9
2
|
8
-
|
u2
=-12 |
 |
4
-
|
2
-
|
3
13
|
8
2
|
u3
=-6 |
0
-
|
0
-
|
0
-
|
0
13
|
u4
=2 |
| v1
=6 |
v2
=-6 |
v3
=-3 |
v4
=2 |
Система для плана 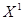 имеет вид: имеет вид: 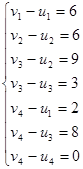
Полагая u1
=0, находим значения всех потенциалов: v1
=6, v2
=-6, u2
=-12,v3
=-3, v4
=2, u3
=-6, u4
=2, т.е. (0; -12; -6; 2; 6; -6; -3; 2).
Шаг 2.2. Проверка на оптимальность. Составляем таблицу оценок 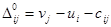 . .
| 0 |
-14 |
-7 |
0 |
u1
=0 |
| 13 |
0 |
0 |
6 |
u2
=-12 |
| ∆1
= |
8 |
-2 |
0 |
0 |
u3
=-6 |
| 4 |
-8 |
-5 |
0 |
u4
=2 |
| v1
=6 |
v2
=-6 |
v3
=-3 |
v4
=2 |
Так как имеются 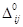 >0, то переходим к шагу 3. >0, то переходим к шагу 3.
Шаг 1.3. Составление нового плана перевозок. 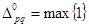 соответствует клетка К21
. соответствует клетка К21
.
-6
  5 5
|
8
-
|
4
-
|
+2
 5 5
|
| ∆1
= |
+5
 - -
|
6
8
|
-9
 2 2
|
8
-
|
4
-
|
2
-
|
+3
 13 13
|
-8
2
|
Θ =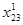 = =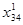 = 2. Возьмем = 2. Возьмем 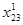 и составим новый план перевозки. и составим новый план перевозки.
Итерация 3.
Шаг 3.1. Вычисление потенциалов
6
3
|
8
-
|
4
-
|
2
7
|
u1
=0 |
5
2
|
6
8
|
9
0
|
8
-
|
u2
=1 |
 |
4
-
|
2
-
|
3
15
|
8
-
|
u3
=7 |
0
-
|
0
-
|
0
-
|
0
13
|
u4
=2 |
| v1
=6 |
v2
=7 |
v3
=10 |
v4
=2 |
Система для плана  имеет вид: имеет вид: 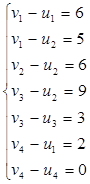
Полагая u1
=0, находим значения всех потенциалов: (0; 1; 7; 2; 6; 7; 10; 2).
Шаг 3.2. Проверка на оптимальность. Составляем таблицу оценок 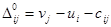 . .
| 0 |
-1 |
6 |
0 |
u1
=0 |
| 0 |
0 |
0 |
-7 |
u2
=1 |
| ∆1
= |
-5 |
-2 |
0 |
-13 |
u3
=7 |
| 4 |
5 |
8 |
0 |
u4
=2 |
| v1
=6 |
v2
=7 |
v3
=10 |
v4
=2 |
Так как имеются 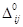 >0, то переходим к шагу 3. >0, то переходим к шагу 3.
Шаг 3.3. Составление нового плана перевозок. 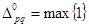 соответствует клетка К43
. соответствует клетка К43
.
-6
  3 3
|
8
-
|
4
-
|
+2
 7 7
|
+5
 2 2
|
6
8
|
-9
 0 0
|
8
-
|
| ∆1
= |
4
-
|
2
-
|
3
15
|
8
-
|
0
-
|
0
-
|
+0
 - -
|
-0
13
|
Θ =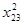 = 0. Составим новый план перевозки. = 0. Составим новый план перевозки.
Итерация 4.
Шаг 4.1. Вычисление потенциалов
6
3
|
8
-
|
4
-
|
2
7
|
u1
=0 |
5
2
|
6
8
|
9
-
|
8
-
|
u2
=1 |
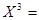 |
4
-
|
2
-
|
3
15
|
8
-
|
u3
=-1 |
0
-
|
0
-
|
0
0
|
0
13
|
u4
=2 |
| v1
=6 |
v2
=7 |
v3
=2 |
v4
=2 |
Система для плана 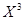 имеет вид: имеет вид: 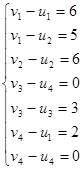
Полагая u1
=0, находим значения всех потенциалов: (0; 1; -1; 2; 6; 7; 2; 2).
Шаг 4.2. Проверка на оптимальность. Составляем таблицу оценок 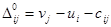 . .
| 0 |
-1 |
-2 |
0 |
u1
=0 |
| 0 |
0 |
-8 |
-7 |
u2
=1 |
| ∆1
= |
3 |
6 |
0 |
-5 |
u3
=-1 |
| 4 |
5 |
0 |
0 |
u4
=2 |
| v1
=6 |
v2
=7 |
v3
=2 |
v4
=2 |
Так как имеются 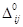 >0, то переходим к шагу 3. >0, то переходим к шагу 3.
Шаг 4.3. Составление нового плана перевозок. 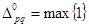 соответствует клетка К32
. соответствует клетка К32
.
-6
  3 3
|
8
-
|
4
-
|
+2
 7 7
|
+5
 2 2
|
-6
 8 8
|
-9
-
|
8
-
|
| ∆1
= |
4
-
|
+2
 - -
|
-3
 15 15
|
8
-
|
0
-
|
0
-
|
+0
 0 0
|
-0
13
|
Θ =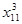 = 3. Составим новый план перевозки. = 3. Составим новый план перевозки.
Итерация 5.
Шаг 5.1. Вычисление потенциалов
6
-
|
8
-
|
4
-
|
2
10
|
u1
=0 |
5
5
|
6
5
|
9
-
|
8
-
|
u2
=-5 |
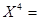 |
4
-
|
2
3
|
3
12
|
8
-
|
u3
=-1 |
0
-
|
0
-
|
0
3
|
0
10
|
u4
=2 |
| v1
=0 |
v2
=1 |
v3
=2 |
v4
=2 |
Система для плана 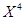 имеет вид: имеет вид: 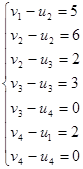
Полагая u1
=0, находим значения всех потенциалов: (0; -5; -1; 2; 0; 1; 2; 2).
Шаг 5.2. Проверка на оптимальность. Составляем таблицу оценок 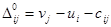 . .
| -6 |
-7 |
-2 |
0 |
u1
=0 |
| 0 |
0 |
-2 |
-1 |
u2
=-5 |
| ∆1
= |
-3 |
0 |
0 |
-5 |
u3
=-1 |
| -2 |
-1 |
0 |
0 |
u4
=2 |
| v1
=0 |
v2
=1 |
v3
=2 |
v4
=2 |
Так как все оценки 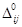 ≤0, следовательно, план ≤0, следовательно, план 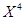 - оптимальный. - оптимальный.
Х оптим
= (0; -5; -1; 2; 0; 1; 2; 2), следовательно, оптимальное значение целевой функции: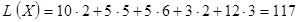 (ден. единиц). (ден. единиц).
Ответ: Х оптим
= (0; -5; -1; 2; 0; 1; 2; 2), L(X) = 117 ден. ед.
|