Содержание
Введение
1. Дискриминантные функции и их геометрическая интерпретация
2. Расчет коэффициентов дискриминантной функции
3. Классификация при наличии двух обучающих выборок
4. Классификация при наличии k
обучающих выборок
5. Взаимосвязь между дискриминантными переменными и дискриминантными функциями
Заключение
Список использованной литературы
Введение
Д
u
скр
u
м
u
нантный анализ
- это раздел математической статистики, содержанием которого является разработка методов решения задач различения (дискриминации) объектов наблюдения по определенным признакам. Например, разбиение совокупности предприятий на несколько однородных групп по значениям каких-либо показателей производственно-хозяйственной деятельности.
Методы дискриминантного анализа находят применение в различных областях: медицине, социологии, психологии, экономике и т.д. При наблюдении больших статистических совокупностей часто появляется необходимость разделить неоднородную совокупность на однородные группы (классы). Такое расчленение в дальнейшем при проведении статистического анализа дает лучшие результаты моделирования зависимостей между отдельными признаками.
Дискриминантный анализ оказывается очень удобным и при обработке результатов тестирования отдельных лиц. Например, при выборе кандидатов на определенную должность можно всех опрашиваемых претендентов разделить на две группы: «подходит» и «не подходит».
Можно привести еще один пример применения дискриминантного анализа в экономике. Для оценки финансового состояния своих клиентов при выдаче им кредита банк классифицирует их на надежных и не надежных по ряду признаков. Таким образом, в тех случаях, когда возникает необходимость отнесения того или иного объекта к одному из реально существующих или выделенных определенным способом классов, можно воспользоваться дискриминантным анализом.
Аппарат дискриминантного анализа разрабатывался многими учеными-специалистами, начиная с конца 50-х годов ХХ в. Дискриминантным анализом, как и другими методами многомерной статистики, занимались П.Ч. Махаланобис, Р. Фишер, Г.Хотеллинг и другие видные ученые.
Все процедуры дискриминантного анализа можно разбить на две группы и рассматривать их как совершенно самостоятельные методы. Первая группа процедур позволяет интерпретировать различия между существующими классами, вторая - проводить классификацию новых объектов в тех случаях, когда неизвестно заранее, к какому из существующих классов они принадлежат.
Реклама

Пусть имеется множество единиц наблюдения - генеральная совокупность. Каждая единица наблюдения характеризуется несколькими признаками (переменными) 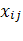 - значение j
-й
переменной у i
-го
объекта i
=1,…N; j=1,…p. - значение j
-й
переменной у i
-го
объекта i
=1,…N; j=1,…p.
Предположим, что все множество объектов разбито на несколько подмножеств (два и более). Из каждого подмножества взята выборка объемом 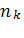 ,
где k
- номер подмножества (класса), k
= 1,... , q
. ,
где k
- номер подмножества (класса), k
= 1,... , q
.
Признаки, которые используются для того, чтобы отличать один класс (подмножество) от другого, называются дискриминантными переменными.
Каждая из этих переменных должна измеряться либо по интервальной шкале, либо по шкале отношений. Интервальная шкала позволяет количественно описать различия между свойствами объектов. Для задания шкалы устанавливаются произвольная точка отсчета и единица измерения. Примерами таких шкал являются календарное время, шкалы температур и т. п. В качестве оценки положения центра используются средняя величина, мода и медиана.
Шкала отношений - частный случай интервальной шкалы. Она позволяет соотнести количественные характеристики какого-либо свойства у разных объектов, например, стаж работы, заработная плата, величина налога.
Теоретически число дискриминантных переменных не ограничено, но на практике их выбор должен осуществляться на основании логического анализа исходной информации и одного из критериев, о котором речь пойдет немного ниже. Число объектов наблюдения должно превышать число дискриминантных переменных, как минимум, на два, т. е. р
< N
.
Дискриминантные переменные должны быть линейно независимыми. Еще одним предположением при дискриминантном анализе является нормальность закона распределения многомерной величины, т.е. каждая из дискриминантных переменных внутри каждого из рассматриваемых классов должна быть подчинена нормальному закону распределения. В случае, когда реальная картина в выборочных совокупностях отличается от выдвинутых предпосылок, следует решать вопрос о целесообразности использования процедур дискриминантного анализа для классификации новых наблюдений, так как в этом случае затрудняются расчеты каждого критерия классификации.
Реклама

1. Дискриминантные функции и их геометрическая интерпретация
Перед тем как приступить к рассмотрению алгоритма дискриминантного анализа, обратимся к его геометрической интерпретации. На рис. 1 изображены объекты, принадлежащие двум различным множествам М1
и М2
.

Рис.1 Геометрическая интерпретация дискриминантной функции и дискриминантных переменных
Каждый объект характеризуется в данном случае двумя переменными 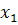 и и 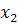 .Если рассматривать проекции объектов (точек) на каждую ось, то эти множества пересекаются, т.е. по каждой переменной отдельно некоторые объекты обоих множеств имеют сходные характеристики. Чтобы наилучшим образом разделить два рассматриваемых множества, нужно построить соответствующую линейную комбинацию переменных .Если рассматривать проекции объектов (точек) на каждую ось, то эти множества пересекаются, т.е. по каждой переменной отдельно некоторые объекты обоих множеств имеют сходные характеристики. Чтобы наилучшим образом разделить два рассматриваемых множества, нужно построить соответствующую линейную комбинацию переменных 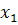 и и 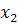 . Для двумерного пространства эта задача сводится к определению новой системы координат. Причем новые оси L
и С должны быть расположены таким образом, чтобы проекции объектов, принадлежащих разным множествам на ось L
,
были максимально разделены. Ось С перпендикулярна оси L
и разделяет два «облака» точек наилучшим образом, Т.е. чтобы множества оказались по разные стороны от этой прямой. При этом вероятность ошибки классификации должна быть минимальной. Сформулированные условия должны быть учтены при определении коэффициентов . Для двумерного пространства эта задача сводится к определению новой системы координат. Причем новые оси L
и С должны быть расположены таким образом, чтобы проекции объектов, принадлежащих разным множествам на ось L
,
были максимально разделены. Ось С перпендикулярна оси L
и разделяет два «облака» точек наилучшим образом, Т.е. чтобы множества оказались по разные стороны от этой прямой. При этом вероятность ошибки классификации должна быть минимальной. Сформулированные условия должны быть учтены при определении коэффициентов 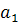 и и 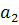 следующей функции: следующей функции:
F(x) = 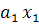 + +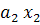 (1) (1)
Функция F(x) называется канонической дискриминантной функцией,
а величины 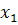 и и 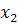 - дискриминантными переменными. - дискриминантными переменными.
Обозначим 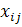 - среднее значение j
-го
признака у объектов i
-го
множества (класса). Тогда для множества М1
среднее значение функции - среднее значение j
-го
признака у объектов i
-го
множества (класса). Тогда для множества М1
среднее значение функции 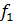 (x) будет равно: (x) будет равно:
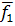 (x) = (x) = 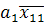 + +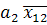 ; (2) ; (2)
Для множества М2
среднее значение функции 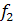 равно: равно:
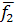 (x) = (x) = 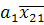 + +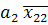 ; (3) ; (3)
Геометрическая интерпретация этих функций - две параллельные прямые, проходящие через центры классов (множеств) (рис.2).

Рис. 2. Центры разделяемых множеств и константа дискриминации
Дискриминантная функция может быть как линейной, так и нелинейной. Выбор ее вида зависит от геометрического расположения разделяемых классов в пространстве дискриминантных переменных. Для упрощения выкладок в дальнейшем рассматривается линейная дискриминантная функция.
2. Расчет коэффициентов дискриминантной функции
Коэффициенты дискриминантной функции 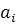 определяются таким образом, чтобы определяются таким образом, чтобы 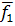 (x) и (x) и 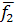 (x) как можно больше различались между собой, т.е. чтобы для двух множеств (классов) было максимальным выражение (x) как можно больше различались между собой, т.е. чтобы для двух множеств (классов) было максимальным выражение
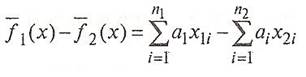
(4)
Тогда можно записать следующее:
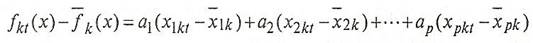 (5) (5)
где k- номер группы; p – число переменных, характеризующих каждое наблюдение.
Обозначим дискриминантную функцию 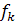 (x)как (x)как 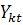 (
k
-
номер группы, t
- номер наблюдения в группе). Внутригрупповая вариация может быть измерена суммой квадратов отклонений: (
k
-
номер группы, t
- номер наблюдения в группе). Внутригрупповая вариация может быть измерена суммой квадратов отклонений:
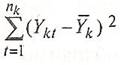 (6) (6)
По обеим группам это будет выглядеть следующим образом:
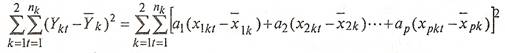 (7) (7)
В матричной форме это выражение может быть записано так:
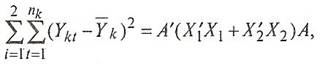 (8) (8)
где А
- вектор коэффициентов дискриминантной функции;
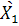 - транспонированная матрица отклонений наблюдаемых значений исходных переменных от их средних величин в первой группе - транспонированная матрица отклонений наблюдаемых значений исходных переменных от их средних величин в первой группе
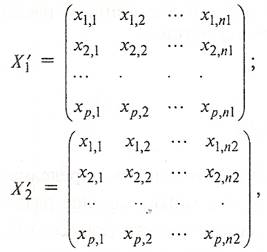 (9) (9)
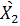 - аналогичная матрица для второй группы. - аналогичная матрица для второй группы.
Объединенная ковариационная матрица 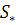 определяется так: определяется так:
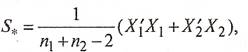 (10) (10)
Следовательно выражение (8) дает оценку внутригрупповой вариации и его можно записать в виде:
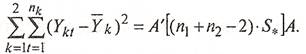 (11) (11)
Межгрупповая вариация может быть измерена как
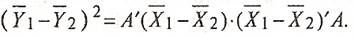 (12) (12)
При нахождении коэффициентов дискриминантной функции 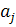 следует исходить из того, что для рассматриваемых объектов внутригрупповая вариация должна быть минимальной, а межгрупповая вариация - максимальной. В этом случае мы достигнем наилучшего разделения двух групп, т.е. необходимо, чтобы величина F
была максимальной: следует исходить из того, что для рассматриваемых объектов внутригрупповая вариация должна быть минимальной, а межгрупповая вариация - максимальной. В этом случае мы достигнем наилучшего разделения двух групп, т.е. необходимо, чтобы величина F
была максимальной:
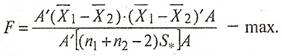 (13) (13)
В точке, где функция F
достигает максимума, частные производные по 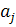 будут равны нулю. Если вычислить частные производные будут равны нулю. Если вычислить частные производные
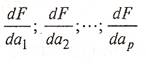 (14) (14)
и приравнять их нулю, то после преобразований получим выражение:
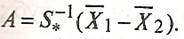 (15) (15)
Из этой формулы и определяется вектор коэффициентов дискриминантной функции (А)
Полученные значения коэффициентов подставляют в формулу (1) и для каждого объекта в обеих группах (множествах) вычисляют дискриминантные функции, затем находят среднее значение для каждой группы. Таким образом, каждое i
-
е наблюдение, которое первоначально описывалось m переменными, будет как бы перемещено в одномерное пространство, т.е. ему будет соответствовать одно значение дискриминантной функции, следовательно, размерность признакового пространства снижается.
3. Классификация при наличии двух обучающих выборок
Перед тем как приступить непосредственно к процедуре классификации, нужно определить границу, разделяющую в частном случае две рассматриваемые группы. Такой величиной может быть значение функции, равноудаленное от 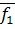 и и 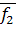 , т.е. , т.е.
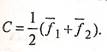 (16) (16)
Величина С называется константой дискриминации.
На рис.1 видно, что объекты, расположенные над прямой f(x)=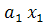 + +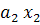 +…+ +…+ 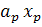 =C , находятся ближе к центру множества =C , находятся ближе к центру множества 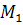 и, следовательно, могут быть отнесены к первой группе, а объекты, расположенные ниже этой прямой, ближе к центру второго множества, т.е. относятся ко второй группе. Если граница между группами выбрана так, как сказано выше, то суммарная вероятность ошибочной классификации минимальная. и, следовательно, могут быть отнесены к первой группе, а объекты, расположенные ниже этой прямой, ближе к центру второго множества, т.е. относятся ко второй группе. Если граница между группами выбрана так, как сказано выше, то суммарная вероятность ошибочной классификации минимальная.
Рассмотрим пример использования дискриминантного анализа для проведения многомерной классификации объектов. При этом в качестве обучающих будем использовать сначала две выборки, принадлежащие двум классам, а затем обобщим алгоритм классификации на случай k классов.
Пример 1.
Имеются данные по двум группам промышленных предприятий машиностроительного комплекса:
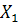 -фондоотдача основных производственных фондов, руб.; -фондоотдача основных производственных фондов, руб.;
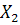 -затраты на рубль произведенной продукции, коп.; -затраты на рубль произведенной продукции, коп.;
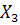 -затраты на сырье и материалов на один рубль продукции, коп. -затраты на сырье и материалов на один рубль продукции, коп.
| Номер
|
Х
1
|
Х
2
|
ХЗ
|
| предприятия
|
| 1 |
0,50 |
94,0 |
8,50 |
| l-я группа |
2 |
0,67 |
75,4 |
8,79 |
| 3 |
0,68 |
85,2 |
9,10 |
| 4 |
0,55 |
98,8 |
8,47 |
| 5 |
1,52 |
81,5
|
4,95 |
| 2-я группа |
6 |
1,20 |
93,8 |
6,95 |
| 7 |
1,46 |
86,5
|
4,70 |
Необходимо провести классификацию четырех новых предприятий, имеющих следующие значения исходных переменных:
l-е предприятие: 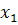 = 1,07, = 1,07, 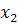 =93,5, =93,5, 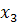 =5,30, =5,30,
2-е предприятие: 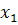 = 0,99, = 0,99, 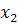 =84,0, =84,0, 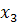 =4,85, =4,85,
3-е предприятие: 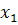 = 0,70, = 0,70, 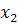 =76,8, =76,8, 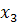 =3,50, =3,50,
4-е предприятие: 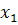 = 1,24, = 1,24, 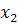 =88,0, =88,0, 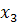 =4,95. =4,95.
Для удобства запишем значения исходных переменных для каждой группы предприятий в виде матриц 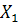 и и 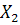 : :
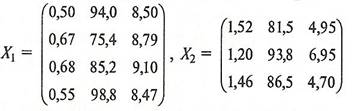 (17) (17)
Рассчитаем среднее значение каждой переменной в отдельных группах для определения положения центров этих групп:
I гр. 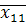 =0,60, =0,60, 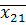 =88,4, =88,4, 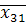 =8,72 =8,72
II гр. 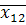 =1,39, =1,39, 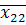 =87,3, =87,3, 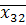 =5,53. =5,53.
Дискриминантная функция f(x)в данном случае имеет вид:
f
(х)
= 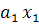 + +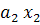 + +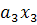 (18) (18)
Коэффициенты 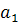 , , 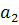 и и 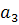 вычисляются по формуле: вычисляются по формуле:
A=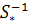 ( (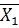 - -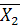 ), (19) ), (19)
где 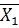 и и 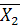 - векторы средних в первой и второй группах; А
- вектор коэффициентов; - векторы средних в первой и второй группах; А
- вектор коэффициентов; 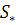 - матрица, обратная совместной ковариационной матрице. - матрица, обратная совместной ковариационной матрице.
Для определения совместной ковариационной матрицы 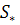 нужно рассчитать матрицы нужно рассчитать матрицы 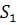 и и 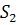 . Каждый элемент этих матриц представляет собой разность между соответствующим значением исходной переменной . Каждый элемент этих матриц представляет собой разность между соответствующим значением исходной переменной 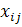 и средним значением этой переменной в данной группе и средним значением этой переменной в данной группе 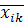 (
k
- номер группы): (
k
- номер группы):
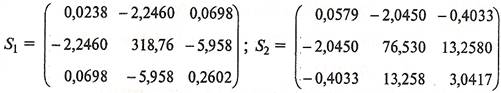
Тогда совместная ковариационная матрица 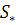 будет равна: будет равна:
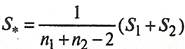 , (20) , (20)
где 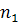 , , 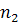 - число объектов l-й и 2-й группы; - число объектов l-й и 2-й группы;
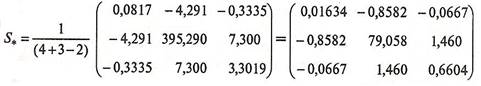 (21) (21)
Обратная матрица 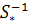 будет равна: будет равна:
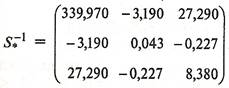 .(22) .(22)
Отcюда находим вектор коэффициентов дискриминантной функции по формуле:
 (23) (23)
т.е. 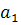 =-185,03, =-185,03, 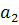 =1,84, =1,84, 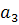 =4,92. =4,92.
Подставим полученные значения коэффициентов в формулу (18) и рассчитаем значения дискриминантной функции для каждого объекта:
 (24) (24)
Тогда константа дискриминации С будет равна:
С = (94,4238-70,0138) = 12,205. (94,4238-70,0138) = 12,205.
После получения константы дискриминации можно проверить правильность распределения объектов в уже существующих двух классах, а также провести классификацию новых объектов.
Рассмотрим, например, объекты с номерами 1, 2, З, 4. Для того чтобы отнести эти объекты к одному из двух множеств, рассчитаем для них значения дискриминантных функций (по трем переменным):
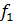 = -185,03 х 1,07 + 1,84 х 93,5 + 4,92 х 5,30 = 0,1339, = -185,03 х 1,07 + 1,84 х 93,5 + 4,92 х 5,30 = 0,1339,
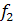 = -185,03 х 0,99 + 1,84 х 84,0 + 4,92 х 4,85 = -4,7577, = -185,03 х 0,99 + 1,84 х 84,0 + 4,92 х 4,85 = -4,7577,
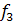 = -185,03 х 0,70 + 1,84 х 76,8 + 4,92 х 3,50 = 29,0110, = -185,03 х 0,70 + 1,84 х 76,8 + 4,92 х 3,50 = 29,0110,
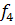 = -185,03 х 1,24 + 1,84 х 88,0 + 4,92 х 4,95 = -43,1632. = -185,03 х 1,24 + 1,84 х 88,0 + 4,92 х 4,95 = -43,1632.
Таким образом, объекты 1, 2 и 4 относятся ко второму классу, а объект 3 относится к первому классу, так как 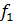 < с, < с, 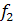 < с, < с, 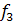 > с, > с, 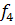 < с. < с.
4. Классификация при наличии
k
обучающих выборок
При необходимости можно проводить разбиение множества объектов на k
классов (при k
>
2). В этом случае нужно рассчитать k
дискриминантных функций, так как классы будут отделяться друг от друга индивидуальными разделяющими поверхностями. На рис. 3 показан случай с тремя множествами и тремя дискриминантными переменными:

Рис.3 Три класса объектов и разделяющие их прямые
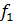 – первая, – первая,
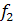 – вторая, – вторая,
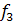 - третья дискриминантные функции. - третья дискриминантные функции.
Пример
2.
Рассмотрим случай, когда существует три класса (множества) объектов. Для этого к двум классам из предыдущего примера добавим еще один. В этом случае будем иметь уже три матрицы исходных данных:
 (25) (25)
Если в процессе дискриминации используются все четыре переменные (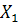 , ,
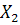 , ,
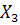 , ,
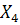 )
то для каждого класса дискриминантные функции имеют вид: )
то для каждого класса дискриминантные функции имеют вид:
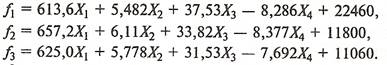 (26) (26)
Определим теперь, к какому классу можно отнести каждое из четырех наблюдений, приведенных в табл.2:
Таблица 2- Исходные данные
Номер
наблюдения
|
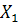 |
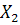 |
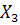 |
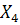 |
| 1 |
1,07 |
93,5 |
5,30 |
5385 |
| 2 |
0,99 |
84,0 |
4,85 |
5225 |
| 3 |
0,70 |
76,8 |
3,50 |
5190 |
| 4 |
1,24 |
88,0 |
4,95 |
6280 |
Подставим соответствующие значения переменных 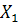 , , 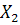 , , 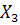 , , 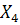 в выражение (26) и вычислим затем разности: в выражение (26) и вычислим затем разности:
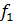 - -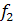 =-20792,082+31856,41=11064,328 =-20792,082+31856,41=11064,328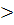 0, 0,
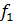 - -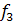 =-20792,082+40016,428=19224,346 =-20792,082+40016,428=19224,346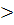 0. 0.
Следовательно, наблюдение 1 в табл.2 относится к первому классу. Аналогичные расчеты показывают, что и остальные три наблюдения следует отнести тоже к первому классу.
Чтобы показать влияние числа дискриминантных переменных на результаты классификации, изменим условие последнего примера. Будем использовать для расчета дискриминантных функций только три переменные: 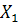 , , 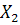 , , 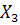 . В этом случае выражения для дискриминантныx функций будут иметь вид: . В этом случае выражения для дискриминантныx функций будут иметь вид:
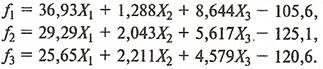 (27) (27)
Подставив в эти выражения значения исходных переменных для классифицируемых объектов, нетрудно убедиться, что все они попадают в третий класс, так как
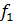 - -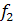 =-26,87 =-26,87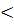 0, 0,
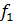 - -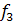 =-37,68 =-37,68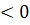 , ,
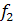 - -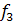 =-10,809 =-10,809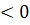 . .
Таким образом, мы видим, что изменение числа переменныx сильно влияет на результат дискриминантного анализа. Чтобы судить о целесообразности включения (удаления) дискриминантной переменной, обычно используют специальные статистические критерии, позволяющие оценить значимость ухудшения или улучшения разбиения после включения (удаления) каждой из отобранных переменных.
5. Взаимосвязь между дискриминантными переменными и дискриминантными функциями
Для оценки вклада отдельной переменной в значение дискриминантной функции целесообразно пользоваться стандартизованными коэффициентами дискриминантной функции. Стандартизованные коэффициенты можно рассчитать двумя путями:
·стандартизовать значения исходных переменных таким образом, чтобы их средние значения были равны нулю, а' дисперсии - единице;
·вычислить стандартизованные коэффициенты исходя из значений коэффициентов в нестандартной форме:
·
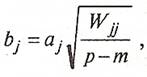 (28) (28)
где р
- общее число исходных переменных, т
- число групп, 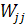 - элементы матрицы ковариаций: - элементы матрицы ковариаций:
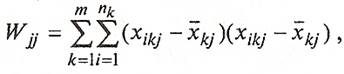 (29) (29)
где i
- номер наблюдения, j - номер переменной, k
- номер класса, 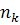 - количество объектов в k
-
мклассе. - количество объектов в k
-
мклассе.
Стандартизованные коэффициенты применяют в тех случаях, когда нужно определить, какая из используемых переменных вносит наибольший вклад в величину дискриминантной функции. В примере с двумя классами, рассмотренном выше, дискриминантная функция имела вид:
f
= -185,03Х1
+ 1,84Х2
+ 4,92Хз
.
Следовательно, наибольший вклад в величину дискриминантной функции вносит переменная X
1
.
Определим значения стандартизованных коэффициентов и запишем новое значение дискриминантной функции:
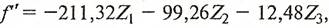 (30) (30)
где 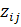 = =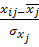
Стандартизованные коэффициенты дискриминантной функции тоже показывают определяющее влияние первой переменной на величину дискриминантной функции.
Помимо определения вклада каждой исходной переменной в дискриминантную функцию, можно проанализировать и степень корреляционной зависимости между ними.
Для оценки тесноты связи между отдельными переменными и дискриминантными функциями служат коэффициенты корреляции, которые называются структурными коэффициентами. Повеличине структурных коэффициентов судят о связи между переменными и дискриминантными функциями. Структурные коэффициенты позволяют также в случае необходимости присвоить имя
каждой функции. Они могут быть рассчитаны в целом по всей совокупности объектов (
R
)
и для каждого класса отдельно (
R
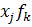 ). ).
Покажем на примере 1 расчет структурных коэффициентов в целом для трех классов. Исходные данные для расчета коэффициентов представлены в табл. 3. Вычисленные структурные коэффициенты (
R
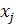 f
)
имеют следующие значения: f
)
имеют следующие значения:
Rx
1
f
=
0,650 RX
2
f
= -0,576 R
ХЗ
f
= -0,506 Rx
4
f
= -0,951
Rx
1
jl
= -0,036 Rx
2
j
1
= 0,486 R
хЗ
jl
= -0,211 Rx
4
j
1
= 0,217
Rx
1
f
2
= -0,728 Rx
2
f
2
= 0,878 R
ХЗ
f
2
= 0,511 Rx
4
f
2
= -0,998
Rx
1
fJ
= -0,713 R
х1
J
З
= 0,258 R
хЗ
fJ
= -0,122 Rx
4
fJ
= -0,998.
Таблица 3 – Исходные данные
| Номер
|
Х1
|
Х
2
|
ХЗ
|
Х
4
|
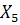 |
| наблюдения
|
| 1 |
0,50 |
94,0 |
8,50 |
6707 |
-31973,089 |
| 2 |
0,67 |
75,4 |
8,79 |
5037 |
-18122,238 |
| 3 |
0,68 |
85,2 |
9,10 |
3695 |
-6930,930 |
| 4 |
0,55 |
98,8 |
8,47 |
6815 |
-32812,109 |
| 5 |
1,52 |
81,5 |
4,95 |
3211 |
-13434,229 |
| 6 |
1,20 |
93,8 |
6,95 |
2890 |
-10812,723 |
| 7 |
1,46 |
86,5 |
4,70 |
2935 |
-11139,514 |
| 8 |
1,70 |
80,0 |
4,50 |
3510 |
-14272,295 |
| 9 |
1,65 |
85,0 |
4,80 |
2900 |
-9573,076 |
| 10 |
1,49 |
78,5 |
4,10 |
2850 |
-9348,104 |
Если рассматривать абсолютные значения структурных коэффициентов, видно, например, что наибольшая зависимость функций 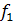 наблюдается от переменной наблюдается от переменной 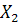 ,
а функций ,
а функций 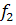 и и 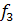 -
от переменной -
от переменной 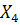 . .
Различные знаки у структурных коэффициентов можно интерпретировать следующим образом. Исходные переменные, имеющие различное направление связи с дискриминантной функцией, т.е. положительные или отрицательные структурные коэффициенты, будут ориентировать объекты в различных направлениях, удаляя или приближая их к центрам соответствующих классов. Из данного примера видно, что переменная X
1
и функция 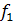 имеют коэффициент -0,036. Это значит, что при увеличении значений имеют коэффициент -0,036. Это значит, что при увеличении значений 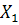 функция функция 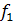 уменьшается. Допустим, все разности ( уменьшается. Допустим, все разности (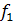 - -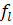 )> о ( l= 2, ... , k
)
для i-го наблюдения, значит его следует отнести к первому классу. Если у классифицируемых объектов значения переменной )> о ( l= 2, ... , k
)
для i-го наблюдения, значит его следует отнести к первому классу. Если у классифицируемых объектов значения переменной 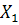 будут возрастать, то значения функции будут возрастать, то значения функции 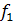 для этих объектов будут уменьшаться, что приведет к отдалению их от центра первого класса. В конце концов для этих объектов будут уменьшаться, что приведет к отдалению их от центра первого класса. В конце концов 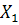 достигнет у p
-го
объекта «критического» значения, которому будет соответствовать неравенство ( достигнет у p
-го
объекта «критического» значения, которому будет соответствовать неравенство (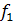 - -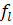 )< 0, т.е. i-й объект уже не попадет в первый класс. Аналогичные рассуждения проводятся и для положительных структурных коэффициентов. )< 0, т.е. i-й объект уже не попадет в первый класс. Аналогичные рассуждения проводятся и для положительных структурных коэффициентов.
Заключение
Дискриминантный анализ так же, как и кластерный анализ, относится к методам многомерной классификации, но при этом базируется на иных предпосылках. Основное отличие заключается в том, что в ходе дискриминантного анализа новые кластеры не образуются, а формулируется правило, по которому новые единицы совокупности относятся к одному из уже существующих множеств (классов). Основанием для отнесения каждой единицы совокупности к определенному множеству служит величина дискриминантной функции, рассчитанная по соответствующим значениям дискриминантных переменных.
Основными проблемами дискриминантного анализа являются, во-первых, определение набора дискриминантных переменных, Bo-вторых, выбор вида дискриминантной функции. Существуют различные критерии последовательного отбора переменных, позволяющих получить наилучшее различение множеств. Можно также воспользоваться алгоритмом пошагового дискриминантного анализа, который в литературе подробно описан. После уточнения оптимального набора дискриминантных переменных исследователю предстоит решить вопрос о выборе вида дискриминантной функции, Т.е. выбрать вид разделяющей поверхности. Чаще всего на практике применяют линейный дискриминантный анализ. В этом случае дискриминантная функция представляет собой либо прямую, либо плоскость (гиперплоскость).
Линейная дискриминантная функция не всегда подходит в качестве описания разделяющей поверхности между множествами. Например, в тех случаях, когда различаемые множества не являются выпуклыми, правомерно предположить, что дискриминантная функция, приводящая к наименьшим ошибкам классификации, не может быть линейной.
Если множества, используемые в качестве обучающих выборок, близко расположены друг к другу, то возрастает вероятность ошибочной классификации новых объектов, особенно в тех случаях, когда классифицируемый объект сильно удален от центров обоих множеств. Складывается ситуация, при которой распознавание объекта затруднено. Одним из возможных выходов в таком случае является пересмотр набора дискриминантных переменных.
Дискриминантный анализ можно использовать как метод прогнозирования (предсказания) поведения наблюдаемых единиц статистической совокупности на основе имеющихся стереотипов поведения аналогичных объектов, входящих в состав объективно существующих или сформированных по определенному принципу множеств (обучающих выборок).
Список использованной литературы
1. Многомерный статистический анализ в экономике. Под редакцией В.Н. Тамашевича. Москва.1999г.
2. Эконометрика и эконометрическое прогнозирование. Мухамедиев Б.М. Алматы. 2007г.
3. Многомерные статистические методы. Дубров А.М., Мхитарян В.С., Трошин Л.И. Москва. 2003г.
4. Эконометрика. Под редакцией Елисеевой И.И. Москва. 2005г.
5. Эконометрика. Балдин С.В., Быстров О.Ф., Соколов М.М. Москва. 2004г.
|