Федеральное агентство по образованию
Новокузнецкий филиал-институт
ГОУ ВПО «Кемеровский государственный университет»
Кафедра информационных систем и управления им. В.К. Буторина
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Теория управления»
Методы безусловной многомерной оптимизации
(Вариант 20)
Выполнили: студенты IV курса
группы ПИЭ - 061
Тимохова А.В.
Годун И.А.
Руководитель: ассистент
кафедры ИСУ
Щепетов
Алексей
Викторович
Новокузнецк 2009
1 Задача об оптимальном распределении инвестиций
Задача: Распределить Т = 100 ден.ед. по четырем предприятиям с целью получения максимальной суммарной прибыли. Прибыль с предприятий задается таблицей 1.1.
Таблица 1.1
| X |
g1 |
g2 |
g3 |
g4 |
| 0 |
0 |
0 |
0 |
0 |
| 20 |
11 |
24 |
12 |
35 |
| 40 |
26 |
22 |
28 |
33 |
| 60 |
31 |
32 |
37 |
36 |
| 80 |
42 |
41 |
47 |
40 |
| 100 |
58 |
59 |
53 |
54 |
Процесс оптимизации разобьем на n шагов (в нашей задаче n =4). На k-м шаге будем оптимизировать инвестирование не всех предприятий, а только с k-го по n-е. При этом на них расходуются не все средства, а некоторая меньшая сумма Ck≤Т, которая и будет являться переменной состояния системы. Переменной управления на k-м шаге назовем величину xk средств, вкладываемых в k-ое предприятие. В качестве функции Беллмана Fk(Ck) на k-м шаге в этой задаче можно выбрать максимально возможную прибыль, которую можно получить с предприятий с k-го по n-е при условии, что на их инвестирование осталось Ck средств. Очевидно, что при вложении в k-е предприятие xk средств получим прибыль gk(xk), а система в (k+1)-му шагу перейдет в состояние Ck+1 = Ck – xk, т.е. на инвестирование предприятий с (k+1)-ого до n-го останется Ck+1 средств.
Таким образом, на первом шаге условной оптимизации при k=n функция Беллмана представляет собой прибыль только с n-го предприятия. При этом на его инвестирование может выделяться количество средств Ck, 0≤Ck≤Т. Очевидно, чтобы получить максимум прибыли с этого последнего последнего предприятия, надо вложить в него все эти средства, т.е. Fn(Cn)=gn(Cn) и xn=Cn.
На каждом из последующих шагов для вычисления функции Беллмана следует использовать результаты предыдущего шага. Максимально возможная прибыль, которая может быть получена предприятиями с k-го по n-е, равна:
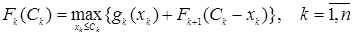 . .
Максимум этого выражения достигается на некотором значении x*k, которое и является оптимальным управлением на k-м шаге для состояния системы Ck. Аналогично можно отыскать функции Беллмана и оптимальные управления вплоть до шага k=1.
Реклама

Функция Беллмана F1(C1) представляет собой максимально возможную прибыль со всех предприятий (с 1-го по n-е), а значение x*k, на котором достигается максимум прибыли, является оптимальным количеством средств, которые необходимо вложить в 1-е предприятие. Далее, для всех последующих шагов вычисляется величина Ck = Ck-1 – Xk и оптимальным управлением на k-м шаге является то значение Xk, которое доставляет максимум прибыли при соответствующем состоянии системы Ck.
Решение.
Этап I. Условная оптимизация.
Шаг 1. k = 4. Предполагаем, что все средства 100 ден.ед. переданы на инвестирование третьего предприятия. В этом случае максимальная прибыль составит F4(C4) = 54, см. таблицу 1.2.
Таблица 1.2
| С4 |
x4 |
F4(C4) |
X*4 |
| 0 |
20 |
40 |
60 |
80 |
100 |
| 0 |
0 |
– |
– |
– |
– |
– |
0 |
0 |
| 20 |
– |
35 |
– |
– |
– |
– |
35 |
20 |
| 40 |
– |
– |
33 |
– |
– |
– |
33 |
40 |
| 60 |
– |
– |
– |
36 |
– |
– |
36 |
60 |
| 80 |
– |
– |
– |
– |
40 |
– |
40 |
80 |
| 100 |
– |
– |
– |
– |
– |
54 |
54 |
100 |
Шаг 2. k = 3. Определяем оптимальную стратегию инвестирования во второе и третье предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид:
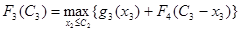 . .
На его основании рассчитываются данные таблицы 1.3.
Таблица 1.3
| С3 |
x3 |
F3(C3) |
X*3 |
| 0 |
20 |
40 |
60 |
80 |
100 |
| 0 |
0 |
0 |
0 |
| 20 |
35 |
12 |
35 |
0 |
| 40 |
33 |
47 |
28 |
47 |
20 |
| 60 |
36 |
45 |
63 |
37 |
63 |
40 |
| 80 |
40 |
48 |
61 |
72 |
47 |
72 |
60 |
| 100 |
54 |
52 |
64 |
70 |
82 |
53 |
82 |
80 |
Шаг 3. k = 2. Определяем оптимальную стратегию инвестирования в первое и остальные предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид:
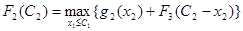 . .
На его основе находятся данные таблицы 1.4.
Таблица 1.4
| С2 |
x2 |
F2(C2) |
X*2 |
| 0 |
20 |
40 |
60 |
80 |
100 |
| 0 |
0 |
0 |
0 |
| 20 |
35 |
24 |
35 |
0 |
| 40 |
47 |
59 |
22 |
59 |
20 |
| 60 |
63 |
71 |
57 |
32 |
71 |
20 |
| 80 |
72 |
87 |
69 |
67 |
41 |
87 |
20 |
| 100 |
82 |
96 |
85 |
79 |
76 |
59 |
96 |
20 |
Шаг 4. k = 1. Определяем оптимальную стратегию инвестирования в первое и остальные предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид:
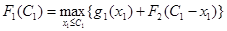 . .
На его основе находятся данные таблицы 1.5.
Таблица 1.5
| С1 |
x1 |
F1(C1) |
X*1 |
| 0 |
20 |
40 |
60 |
80 |
100 |
| 0 |
0 |
0 |
0 |
| 20 |
35 |
11 |
35 |
0 |
| 40 |
59 |
46 |
26 |
59 |
0 |
| 60 |
71 |
70 |
61 |
31 |
71 |
0 |
| 80 |
87 |
82 |
85 |
66 |
42 |
87 |
0 |
| 100 |
96 |
98 |
97 |
90 |
77 |
58 |
98 |
20 |
Этап II. Безусловная оптимизация.
Шаг 1. По данным таблицы 1.5 максимальный доход при распределении 100 ден.ед. между тремя предприятиями составляет F1= 98. При этом первому предприятию нужно выделить x1 = 20 ден.ед.
Шаг 2. Определяем величину оставшихся денежных средств, приходящуюся на долю второго и третьего предприятий:
С2 = С1 – x*1 = 100 – 20 = 80.
По данным таблицы 1.4 находим, что оптимальный вариант распределения денежных средств размером 80 ден.ед. между вторым, третьим и четвертым предприятиями составляет F2 = 96 ден.ед. при выделении второму x2 = 20 ден.ед.
Шаг 3. Определяем величину оставшихся денежных средств, приходящуюся на долю третьего и четвертого предприятия:
С3 = С2 – x*2 = 80 – 20 = 60.
Из таблицы 1.3 находим F3 = 63 и x*3 = 40 ден.ед. При этом получается что x*4 = 20 ден.ед. и F4 = 35.
Таким образом, оптимальный план инвестирования предприятий
X* = (20,40,20,20),
обеспечивающий максимальный доход
F(100) = g1(20) + g2(40) + g3(20) + g4(20) = 11 + 24 + 28 + 35 = 98 ден.ед.
Реклама

Ответ: Максимальная суммарная прибыль по четырем предприятиям составляет 98 ден.ед.
2 Задача выбора оптимального пути в транспортной сети
Задача: В предложенной транспортной сети (см. рисунок 1) имеется несколько маршрутов по проезду из начального пункта (1) в конечный пункт (11). Стоимость проезда между отдельными пунктами транспортной сети представлена в таблице 2.1. Необходимо определить оптимальный маршрут проезда из пункта 1 в пункт 11 с минимальными транспортными расходами.
Рисунок 1

Таблица 2.1
| Начальный путь |
Конечный путь |
T(i,j) |
| 1 |
2 |
5 |
| 1 |
3 |
7 |
| 1 |
4 |
6 |
| 1 |
5 |
10 |
| 2 |
6 |
3 |
| 2 |
7 |
7 |
| 3 |
6 |
8 |
| 3 |
7 |
9 |
| 4 |
6 |
11 |
| 4 |
7 |
4 |
| 5 |
6 |
8 |
| 5 |
7 |
9 |
| 6 |
8 |
4 |
| 6 |
9 |
5 |
| 6 |
10 |
4 |
| 7 |
8 |
5 |
| 7 |
9 |
12 |
| 7 |
10 |
6 |
| 8 |
11 |
10 |
| 9 |
11 |
8 |
| 10 |
11 |
10 |
В данной задаче имеется ограничение – двигаться по магистралям можно только слева направо. Это дает нам возможность разбить всю транспортную сеть на пояса и отнести каждый из десяти пунктов к одному из четырех поясов. Будем говорить, что пункт принадлежит k-му поясу, если из него можно попасть в конечный пункт ровно за k шагов, т.е. заездом ровно в k-1 промежуточный пункт. Таким образом, пункты 8, 9 и 10 принадлежат к первому поясу; 6 и 7 – ко второму; 2, 3, 4 и 5 – к третьему; 1 – к четвертому. На k-м шаге будем находить оптимальные маршруты из городов k-го пояса до конечного пункта.
Оптимизацию будем производить с хвоста процесса, и потому, добравшись до k-го шага, мы не можем знать, в какой именно из городов k-го пояса мы попадем, двигаясь из пункта 1. Поэтому для каждого из этих городов мы должны будем найти оптимальный маршрут до конечного пункта. Очевидно, что минимально возможная стоимость проезда до пункта 11 будет зависеть только от того, в каком из городов этого пояса мы оказались. Номер S города, принадлежащего k-му поясу, и будет называться переменной состояния данной системы на k-м шаге. Нужно помнить, что, добравшись до k-го шага, мы уже осуществили предыдущие шаги, в частности, нашли оптимальные маршруты по перемещению из любого города (k-1)-го пояса в конечный пункт. Таким образом, находясь в некотором городе S k-го пояса, мы должны принять решение о том, в какой из городов (k-1)-го пояса следует отправиться, а направление дальнейшего движения уже известно нам из предыдущих шагов. Номер J города (k-1)-го пояса будет являться переменной управления на k-м шаге.
Функция Беллмана на k-м шаге решения задачи дает нам возможность рассчитать минимальную стоимость проезда из города S (k-го пояса) до конечного пункта. Для первого шага (k=1) эту величину отыскать не сложно – это стоимость проезда из городов 1-го пояса непосредственно до конечного пункта: F1(i)=Ci11. Для последующих же шагов стоимость проезда складывается из двух слагаемых – стоимости проезда из города S k-го пояса в город J (k-1)-го пояса и минимально возможной стоимости проезда из города J до конечного пункта, т.е. Fk-1(J).
Таким образом, функциональное уравнение Беллмана на k-м шаге решения будет иметь вид:
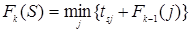
Минимум стоимости достигается на некотором значении J*, которое и является оптимальным направлением движения из пункта S в сторону конечного пункта.
Решение:
Этап I. Условная оптимизация.
Шаг 1. k = 1. F1(S) = ts11.
Таблица 2.2
| S |
J = 11 |
F1(S) |
J* |
| 8 |
10 |
10 |
11 |
| 9 |
8 |
8 |
11 |
| 10 |
10 |
10 |
11 |
Шаг 2. k = 2. Функциональное уравнение на данном шаге принимает вид:
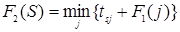 . .
Результаты расчета по приведенной формуле приведены в таблице 2.3:
Таблица 2.3
| S |
J = 8 |
J = 9 |
J = 10 |
F2(S) |
J* |
| 6 |
4 + 10 |
5 + 8 |
4 + 10 |
13 |
9 |
| 7 |
5 + 10 |
12 + 8 |
6 + 10 |
15 |
8 |
Шаг 3. k = 3. Функциональное уравнение на данном шаге принимает вид:
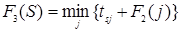 . .
Результаты расчета по приведенной формуле приведены в таблице 2.4:
Таблица 2.4
| S |
J = 6 |
J = 7 |
F3(S) |
J* |
| 2 |
3 + 13 |
7 + 15 |
16 |
6 |
| 3 |
8 + 13 |
9 + 15 |
21 |
6/7 |
| 4 |
11 + 13 |
4 + 15 |
19 |
7 |
| 5 |
8 + 13 |
9 + 15 |
21 |
6/7 |
Шаг 4. k = 4. Функциональное уравнение на данном шаге принимает вид:
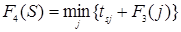 . .
Результаты расчета по приведенной формуле приведены в таблице 2.5:
Таблица 2.5
| S |
J = 2 |
J = 3 |
J = 4 |
J = 5 |
F4(S) |
J* |
| 1 |
5 + 16 |
7 + 21 |
6 + 19 |
10 + 21 |
21 |
2 |
Этап II. Безусловная оптимизация.
На этапе условной оптимизации получено, что минимальные затраты на проезд из пункта 1 в пункт 11 составляют F4(1) = 21, что достигается следующим движением по магистралям. Из пункта 1 следует направиться в пункт 2, затем из него в пункт 6, затем в пункт 9 и из него в пункт 11.
Ответ: Оптимальным маршрутом из пункта 1 в пункт 11 является маршрут 1 – 2 – 6 – 9 – 11.
3 Методы Хэмминга и Брауна
Задача: На эмпирическом временном ряде из 20 значений ( таблица 3.1), используя процедуры обычной регрессии, Хэмминга (А и Б-метод) и Брауна, выполнить прогноз на один шаг и на три-четыре шага вперед для каждого метода соответственно. Сравнить прогнозные процедуры. Сделать выводы.
Таблица 3.1
| t |
Y(t) |
| 1 |
50 |
| 2 |
53 |
| 3 |
56,5 |
| 4 |
53,5 |
| 5 |
51 |
| 6 |
54 |
| 7 |
53,5 |
| 8 |
60 |
| 9 |
59 |
| 10 |
60 |
| 11 |
61 |
| 12 |
62 |
| 13 |
58 |
| 14 |
57 |
| 15 |
57,5 |
| 16 |
59,5 |
| 17 |
60,5 |
| 18 |
61 |
| 19 |
62 |
| 20 |
62,5 |
3.1 Метод Хемминга
Метод Хемминга обладает достоинствами, связанными с простотой и относительно небольшой погрешностью. Существует в двух модификациях. Базовый алгоритм (А-метод Хемминга) применяется для прогнозирования относительно стабильных или слабо изменяющихся динамических рядов, имеющих фиксированную структуру.
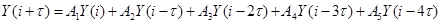 , ,
где 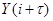 – прогнозное значение; – прогнозное значение;
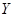 - значение функции; - значение функции;
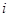 - порядковый номер элемента, входящего в состав исследуемого объекта; - порядковый номер элемента, входящего в состав исследуемого объекта;
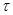 - время запаздывания или исследование обрабатываемых данных (реализация функций объекта); - время запаздывания или исследование обрабатываемых данных (реализация функций объекта);
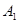 , ,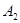 , , , ,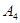 , ,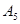 - коэффициенты настройки, задаваемые жестко, в виде числа. - коэффициенты настройки, задаваемые жестко, в виде числа.
Для каждого ряда коэффициенты задаются индивидуально. Число коэффициентов всегда не четное. Сумма всех коэффициентов всегда должна быть равной 1 (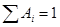 ). ).
Наиболее удачными, по мнению Хемминга, являются коэффициенты для 3 и 5 слагаемых (таблица 3.2).
Таблица 3.2
| А1 |
А2 |
А3 |
А4 |
А5 |
| для трех |
0,60 |
0,30 |
0,10 |
| для пяти |
0,65 |
0,15 |
0,10 |
0,04 |
0,01 |
Данный алгоритм прошел апробацию и достаточно точно прогнозирует переменные различного рода технологических и транспортных операций в нормальном режиме эксплуатации. Однако при применении в случае нештатного и аварийного режимов производства имеет место значительная погрешность, т.е. больше 15%.
Исследования показали, что для увеличения адаптивных возможностей требуется методика настройки коэффициентов, алгоритм которой и включает В-метод Хемминга.
Идея заключается в следующем: в фиксированный момент времени t1 (в который обнаружилось превышение порога погрешности в 5%) рассматривается автокорреляционная функция (АКФ) ряда 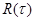 . При этом оценивается величина вклада каждой из компонент . При этом оценивается величина вклада каждой из компонент 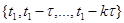 в t2, и рассчитываются соответствующие коэффициенты: в t2, и рассчитываются соответствующие коэффициенты:
Шаг 1: оценивается величина площади под АКФ
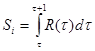 ; ;
Шаг 2: коэффициенты рассчитываются по формуле
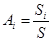 . .
Модифицированный метод проверялся на реальных данных нестационарной динамики, и погрешности не превышали 5-10%, что вполне приемлемо для подобных задач.
Решение:
Результаты моделирования по методу Хэмминга представлены в таблице 3.3.
Таблица 3.3
 |
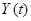 |
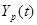 |
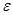 |
| 1 |
50,0 |
50,000 |
0,00 |
| 2 |
53,0 |
53,000 |
0,00 |
| 3 |
56,5 |
54,800 |
1,70 |
| 4 |
53,5 |
54,350 |
0,85 |
| 5 |
51,0 |
52,300 |
1,30 |
| 6 |
54,0 |
53,050 |
0,95 |
| 7 |
53,5 |
53,400 |
0,10 |
| 8 |
60,0 |
57,450 |
2,55 |
| 9 |
59,0 |
58,750 |
0,25 |
| 10 |
60,0 |
59,700 |
0,30 |
| 11 |
61,0 |
60,500 |
0,50 |
| 12 |
62,0 |
61,500 |
0,50 |
| 13 |
58,0 |
59,500 |
1,50 |
| 14 |
57,0 |
57,800 |
0,80 |
| 15 |
57,5 |
57,400 |
0,10 |
| 16 |
59,5 |
58,650 |
0,85 |
| 17 |
60,5 |
59,900 |
0,60 |
| 18 |
61,0 |
60,700 |
0,30 |
| 19 |
62,0 |
61,550 |
0,45 |
| 20 |
62,5 |
62,200 |
0,30 |
| 21 |
61,855 |
| 22 |
61,928 |
| 23 |
61,933 |
| 24 |
61,924 |
Прогнозные значение на основе базового алгоритма Хэмминга (А-метод ):
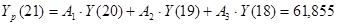 ; ;
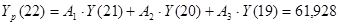 ; ;
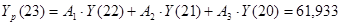 ; ;
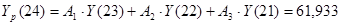 . .
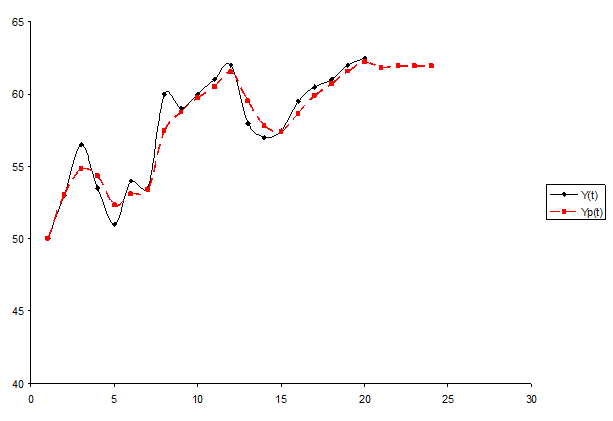
На основе полученных данных построим график прогнозирования по адаптивной модели Хемминга (рисунок 2)
Рисунок 2
Оценим адекватность модели с помощью коэффициента детерминации. Для этого рассчитаем
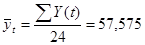 , ,
остальные расчеты представлены в таблице 3.4.
Таблица 3.4
 |
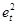 |
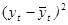 |
| 50,0 |
0,000 |
57,381 |
| 53,0 |
0,000 |
20,931 |
| 56,5 |
2,890 |
1,156 |
| 53,5 |
0,722 |
16,606 |
| 51,0 |
1,690 |
43,231 |
| 54,0 |
0,903 |
12,781 |
| 53,5 |
0,010 |
16,606 |
| 60,0 |
6,503 |
5,881 |
| 59,0 |
0,063 |
2,031 |
| 60,0 |
0,090 |
5,881 |
| 61,0 |
0,250 |
11,731 |
| 62,0 |
0,250 |
19,581 |
| 58,0 |
2,250 |
0,181 |
| 57,0 |
0,640 |
0,331 |
| 57,5 |
0,010 |
0,006 |
| 59,5 |
0,723 |
3,706 |
| 60,5 |
0,360 |
8,556 |
| 61,0 |
0,090 |
11,731 |
| 62,0 |
0,203 |
19,581 |
| 62,5 |
0,090 |
24,256 |
 |
17,735 |
282,138 |
Коэффициент детерминации находится по формуле:
3.2 Метод Брауна
Также считается адаптивным алгоритмом прогнозирования, и в основном используется при краткосрочном прогнозировании.
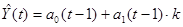 , ,
где k – количество шагов прогнозирования (k=1).
Это значение сравнивается с фактическим уровнем
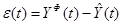 , ,
который затем используется для корректировки модели.
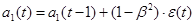 , ,
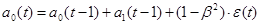 , ,
где 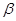 – коэффициент дисконтирования данных, отражает большую степень доверия к более поздним данным, – коэффициент дисконтирования данных, отражает большую степень доверия к более поздним данным, 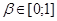 . .
Решение:
Начальные оценки параметров получим по первым пяти точкам (они представлены в таблице 3.5) по формулам:
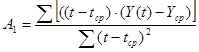 , , 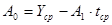
Таблица 3.5
 |
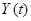 |
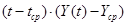 |
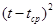 |
| 1 |
50,0 |
5,6 |
4 |
| 2 |
53.0 |
-0,2 |
1 |
| 3 |
56,5 |
0,0 |
0 |
| 4 |
53,5 |
0,7 |
1 |
| 5 |
51,0 |
-3,6 |
4 |
 |
2,5 |
10 |
Для расчета этой таблицы нам понадобилось 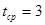 и и 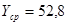 . .
Результаты моделирования по методу Брауна представлены в таблице 3.6.
Таблица 3.6
 |
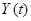 |
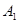 |
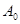 |
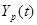 |
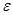 |
| 0 |
0,250 |
52,050 |
| 1 |
50,0 |
-0,578 |
51,472 |
52,300 |
-2,300 |
| 2 |
53,0 |
0,180 |
51,652 |
50,894 |
2,106 |
| 3 |
56,5 |
1,861 |
53,513 |
51,832 |
4,668 |
| 4 |
53,5 |
1,186 |
54,699 |
55,373 |
-1,873 |
| 5 |
51,0 |
-0,572 |
54,126 |
55,885 |
-4,885 |
| 6 |
54,0 |
-0,412 |
53,715 |
53,554 |
0,446 |
| 7 |
53,5 |
-0,341 |
53,374 |
53,303 |
0,197 |
| 8 |
60,0 |
2,167 |
55,541 |
53,033 |
6,967 |
| 9 |
59,0 |
2,632 |
58,173 |
57,708 |
1,292 |
| 10 |
60,0 |
2,342 |
60,516 |
60,806 |
-0,806 |
| 11 |
61,0 |
1,673 |
62,189 |
62,858 |
-1,858 |
| 12 |
62,0 |
1,003 |
63,192 |
63,862 |
-1,862 |
| 13 |
58,0 |
-1,227 |
61,965 |
64,195 |
-6,195 |
| 14 |
57,0 |
-2,573 |
59,392 |
60,738 |
-3,738 |
| 15 |
57,5 |
-2,328 |
57,064 |
56,819 |
0,681 |
| 16 |
59,5 |
-0,613 |
56,451 |
54,737 |
4,763 |
| 17 |
60,5 |
1,065 |
57,517 |
55,839 |
4,661 |
| 18 |
61,0 |
1,936 |
59,452 |
58,582 |
2,418 |
| 19 |
62,0 |
2,156 |
61,608 |
61,388 |
0,612 |
| 20 |
62,5 |
1,701 |
63,309 |
63,764 |
-1,264 |
| 21 |
65,010 |
| 22 |
66,711 |
| 23 |
68,412 |
| 24 |
70,112 |
Для осуществления прогноза на несколько точек вперед рассмотрели полученную на последнем шаге модель
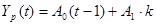
Прогнозные оценки по этой модели получаются подстановкой в нее значений 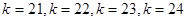 , таким образом: , таким образом:
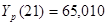 , ,
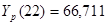 , ,
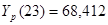 , ,
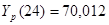 . .
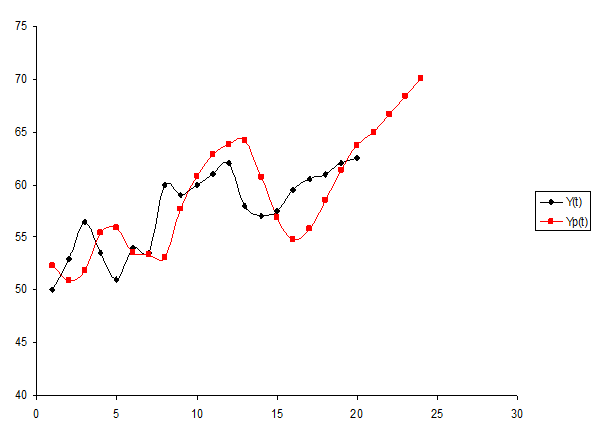
На основе полученных данных построим график прогнозирования по адаптивной модели Брауна (рисунок 3)
Рисунок 3
Оценим адекватность модели с помощью коэффициента детерминации. Для этого рассчитаем
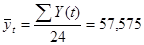 , ,
остальные расчеты представлены в таблице 3.7.
Таблица 3.7
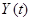 |
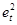 |
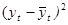 |
| 50 |
5,290 |
57,381 |
| 53 |
4,435 |
20,931 |
| 56,5 |
21,787 |
1,156 |
| 53,5 |
3,509 |
16,606 |
| 51 |
23,863 |
43,231 |
| 54 |
0,199 |
12,781 |
| 53,5 |
0,039 |
16,606 |
| 60 |
48,541 |
5,881 |
| 59 |
1,668 |
2,031 |
| 60 |
0,649 |
5,881 |
| 61 |
3,452 |
11,731 |
| 62 |
3,469 |
19,581 |
| 58 |
38,377 |
0,181 |
| 57 |
13,969 |
0,331 |
| 57,5 |
0,463 |
0,006 |
| 59,5 |
22,690 |
3,706 |
| 60,5 |
21,729 |
8,556 |
| 61 |
5,847 |
11,731 |
| 62 |
0,374 |
19,581 |
| 62,5 |
1,599 |
24,256 |
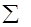 |
221,950 |
282,138 |
Коэффициент детерминации находится по формуле:
Вывод: Сравнивая коэффициенты детерминации по методам Хемминга и Брауна, равные 0,937 и 0,213 соответственно, делаем вывод что модель Хемминга является наиболее адекватной.
4 Идентификация как функция управления
В таблице 4.1 приведены данные о стоимости эксплуатации винтовых самолетов в зависимости от возраста:
Таблица 4.1
| Возраст |
Стоимость |
| 1,0 |
466 |
| 1,0 |
549 |
| 1,0 |
978 |
| 4,0 |
495 |
| 4,0 |
723 |
| 4,0 |
681 |
| 4,5 |
619 |
| 4,5 |
1049 |
| 4,5 |
1033 |
| 5,0 |
163 |
| 5,0 |
182 |
| 5,0 |
890 |
| 5,0 |
1522 |
| 5,0 |
1194 |
| 5,5 |
987 |
| 6,0 |
764 |
| 6,0 |
1373 |
1. Провести процедуру структурно-параметрической идентификации математической модели для исходных данных. Оценить адекватность.
2. Проанализируйте данные, исключив повторы. Ответьте на вопросы: изменилось ли математическая модель? Как изменился коэффициент детерминации? Адекватна ли подобранная модель данным?
Решение:
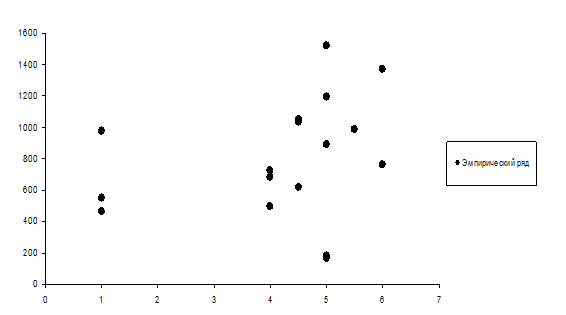
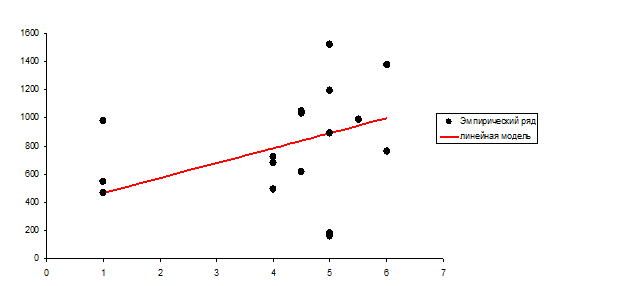
Построим график эмпирических данных (рисунок 4).
Рисунок 4- График эмпирических данных
Проведем все необходимые расчеты для составления статистического уравнения однофакторной зависимости и дальнейшего анализа этой зависимости. Для этого рассмотрим три модели:
прямая однофакторная линейная связь при одновременном увеличении факторного и результативного признаков;
логарифмическая модель (прямая гипербола, когда уровень результативного признака возрастает, а затем его рост приостанавливается, оставаясь почти на одном уровне);
прямая логическая зависимость (когда происходит неустойчивое возрастание уровня результативного признака).
Линейная модель.
Уравнение модели прямой однофакторной линейной связи:
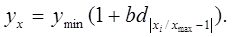
Для вычисления параметра 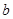 , составления уравнения однофакторной зависимости и дальнейшего анализа этой зависимости заполним таблицу 4.2. , составления уравнения однофакторной зависимости и дальнейшего анализа этой зависимости заполним таблицу 4.2.
Таблица 4.2
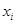 |
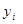 |
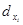 |
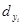 |
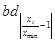 |
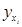 |
| 1,0 |
466 |
0,0 |
0,000 |
0,000 |
466,000 |
| 1,0 |
549 |
0,0 |
0,178 |
0,000 |
466,000 |
| 1,0 |
978 |
0,0 |
1,099 |
0,000 |
466,000 |
| 4,0 |
495 |
3,0 |
0,062 |
0,685 |
785,222 |
| 4,0 |
723 |
3,0 |
0,552 |
0,685 |
785,222 |
| 4,0 |
681 |
3,0 |
0,461 |
0,685 |
785,222 |
| 4,5 |
619 |
3,5 |
0,328 |
0,799 |
838,426 |
| 4,5 |
1049 |
3,5 |
1,251 |
0,799 |
838,426 |
| 4,5 |
1033 |
3,5 |
1,217 |
0,799 |
838,426 |
| 5,0 |
163 |
4,0 |
-0,650 |
0,913 |
891,630 |
| 5,0 |
182 |
4,0 |
-0,609 |
0,913 |
891,630 |
| 5,0 |
890 |
4,0 |
0,910 |
0,913 |
891,630 |
| 5,0 |
1522 |
4,0 |
2,266 |
0,913 |
891,630 |
| 5,0 |
1194 |
4,0 |
1,562 |
0,913 |
891,630 |
| 5,5 |
987 |
4,5 |
1,118 |
1,028 |
944,833 |
| 6,0 |
764 |
5,0 |
0,639 |
1,142 |
998,037 |
| 6,0 |
1373 |
5,0 |
1,946 |
1,142 |
998,037 |
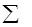 |
54,0 |
12,330 |
Примечание. Предпоследний и последний столбцы таблицы 4.2 заполняются после отыскания параметра уравнения зависимости 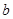 и составления самого уравнения зависимости. и составления самого уравнения зависимости.
В рассматриваемом примере параметр  , при , при 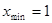 и и 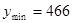 вычисляется по формуле: вычисляется по формуле:
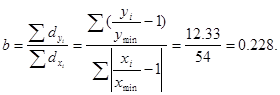
В рассматриваемом примере окончательный вид уравнения зависимости находим по формуле.:
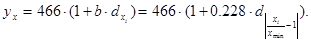
Отобразим эмпирические и теоретические значения результативного признака на графике (рисунок 4).
Рисунок 4
Информация для расчета коэффициента детерминации в типовой задаче в полном объеме представлена в таблице 4.3.
Таблица 4.3
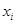 |
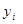 |
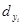 |
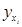 |
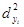 |
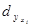 |
(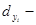 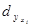 ) ) |
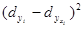 |
| 1,0 |
466 |
0,000 |
466,000 |
0,000 |
0,000 |
0,000 |
0,000 |
| 1,0 |
549 |
0,178 |
466,000 |
0,032 |
0,000 |
0,178 |
0,032 |
| 1,0 |
978 |
1,099 |
466,000 |
1,207 |
0,000 |
1,099 |
1,207 |
| 4,0 |
495 |
0,062 |
785,222 |
0,004 |
0,685 |
-0,623 |
0,388 |
| 4,0 |
723 |
0,552 |
785,222 |
0,304 |
0,685 |
-0,134 |
0,018 |
| 4,0 |
681 |
0,461 |
785,222 |
0,213 |
0,685 |
-0,224 |
0,050 |
| 4,5 |
619 |
0,328 |
838,426 |
0,108 |
0,799 |
-0,471 |
0,222 |
| 4,5 |
1049 |
1,251 |
838,426 |
1,565 |
0,799 |
0,452 |
0,204 |
| 4,5 |
1033 |
1,217 |
838,426 |
1,480 |
0,799 |
0,418 |
0,174 |
| 5,0 |
163 |
-0,650 |
891,630 |
0,423 |
0,913 |
-1,564 |
2,445 |
| 5,0 |
182 |
-0,609 |
891,630 |
0,371 |
0,913 |
-1,523 |
2,319 |
| 5,0 |
890 |
0,910 |
891,630 |
0,828 |
0,913 |
-0,003 |
0,000 |
| 5,0 |
1522 |
2,266 |
891,630 |
5,135 |
0,913 |
1,353 |
1,830 |
| 5,0 |
1194 |
1,562 |
891,630 |
2,441 |
0,913 |
0,649 |
0,421 |
| 5,5 |
987 |
1,118 |
944,833 |
1,250 |
1,028 |
0,090 |
0,008 |
| 6,0 |
764 |
0,639 |
998,037 |
0,409 |
1,142 |
-0,502 |
0,252 |
| 6,0 |
1373 |
1,946 |
998,037 |
3,788 |
1,142 |
0,805 |
0,647 |
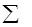 |
12,330 |
19,558 |
10,217 |
По данным таблицы 4.3 коэффициент детерминации составит:
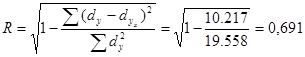
Логарифмическая модель
Уравнение модели прямой гиперболы:
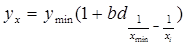
Для вычисления параметра  , составления уравнения однофакторной зависимости и дальнейшего анализа этой зависимости заполним таблицу 4.4. , составления уравнения однофакторной зависимости и дальнейшего анализа этой зависимости заполним таблицу 4.4.
Таблица 4.4
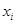 |
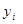 |
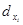 |
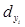 |
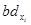 |
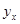 |
| 1,0 |
466 |
0,000 |
0,000 |
0,000 |
466,000 |
| 1,0 |
549 |
0,000 |
0,178 |
0,000 |
466,000 |
| 1,0 |
978 |
0,000 |
1,099 |
0,000 |
466,000 |
| 4,0 |
495 |
0,750 |
0,062 |
1,006 |
934,912 |
| 4,0 |
723 |
0,750 |
0,552 |
1,006 |
934,912 |
| 4,0 |
681 |
0,750 |
0,461 |
1,006 |
934,912 |
| 4,5 |
619 |
0,778 |
0,328 |
1,044 |
952,279 |
| 4,5 |
1049 |
0,778 |
1,251 |
1,044 |
952,279 |
| 4,5 |
1033 |
0,778 |
1,217 |
1,044 |
952,279 |
| 5,0 |
163 |
0,800 |
0,650 |
1,073 |
966,172 |
| 5,0 |
182 |
0,800 |
0,609 |
1,073 |
966,172 |
| 5,0 |
890 |
0,800 |
0,910 |
1,073 |
966,172 |
| 5,0 |
1522 |
0,800 |
2,266 |
1,073 |
966,172 |
| 5,0 |
1194 |
0,800 |
1,562 |
1,073 |
966,172 |
| 5,5 |
987 |
0,818 |
1,118 |
1,098 |
977,540 |
| 6,0 |
764 |
0,833 |
0,639 |
1,118 |
987,013 |
| 6,0 |
1373 |
0,833 |
1,946 |
1,118 |
987,013 |
 |
11,068 |
14,850 |
14,850 |
Примечание. Предпоследний и последний столбцы таблицы 4.4 заполняются после отыскания параметра уравнения зависимости  и составления самого уравнения зависимости. и составления самого уравнения зависимости.
В рассматриваемом примере параметр  , при , при 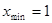 и и 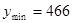 вычисляется по формуле: вычисляется по формуле:
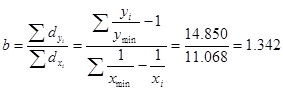
В рассматриваемом примере окончательный вид уравнения зависимости находим по формуле:
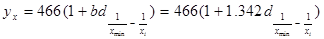
Отобразим эмпирические и теоретические значения результативного признака на графике (рисунок 5).
Рисунок 5
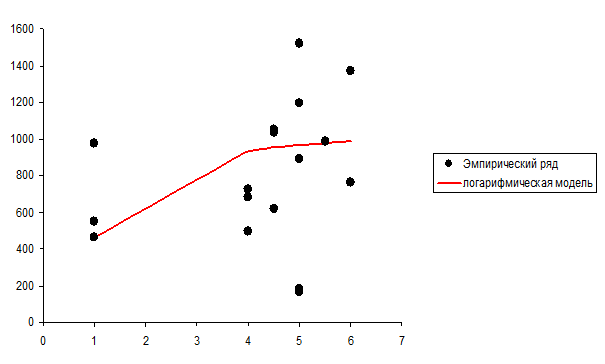
Информация для расчета коэффициента детерминации в типовой задаче в полном объеме представлена в таблице 4.5.
Таблица 4.5
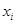 |
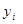 |
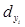 |
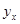 |
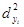 |
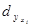 |
(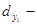 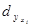 ) ) |
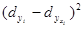 |
| 1,0 |
466 |
0,000 |
466,000 |
0,000 |
0,000 |
0,000 |
0,00000 |
| 1,0 |
549 |
0,178 |
466,000 |
0,032 |
0,000 |
0,178 |
0,03172 |
| 1,0 |
978 |
1,099 |
466,000 |
1,207 |
0,000 |
1,099 |
1,20717 |
| 4,0 |
495 |
0,062 |
934,912 |
0,004 |
1,006 |
-0,944 |
0,89117 |
| 4,0 |
723 |
0,552 |
934,912 |
0,304 |
1,006 |
-0,455 |
0,20679 |
| 4,0 |
681 |
0,461 |
934,912 |
0,213 |
1,006 |
-0,545 |
0,29689 |
| 4,5 |
619 |
0,328 |
952,279 |
0,108 |
1,044 |
-0,715 |
0,51150 |
| 4,5 |
1049 |
1,251 |
952,279 |
1,565 |
1,044 |
0,208 |
0,04308 |
| 4,5 |
1033 |
1,217 |
952,279 |
1,480 |
1,044 |
0,173 |
0,03001 |
| 5,0 |
163 |
0,650 |
966,172 |
0,423 |
1,073 |
-0,423 |
0,17903 |
| 5,0 |
182 |
0,609 |
966,172 |
0,371 |
1,073 |
-0,464 |
0,21519 |
| 5,0 |
890 |
0,910 |
966,172 |
0,828 |
1,073 |
-0,163 |
0,02672 |
| 5,0 |
1522 |
2,266 |
966,172 |
5,135 |
1,073 |
1,193 |
1,42268 |
| 5,0 |
1194 |
1,562 |
966,172 |
2,441 |
1,073 |
0,489 |
0,23902 |
| 5,5 |
987 |
1,118 |
977,540 |
1,250 |
1,098 |
0,020 |
0,00041 |
| 6,0 |
764 |
0,639 |
987,013 |
0,409 |
1,118 |
-0,479 |
0,22903 |
| 6,0 |
1373 |
1,946 |
987,013 |
3,788 |
1,118 |
0,828 |
0,68608 |
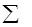 |
14,850 |
19,558 |
6,21649 |
По данным таблицы 4.5 коэффициент детерминации составит:
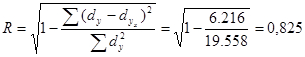
Логическая модель
Уравнение модели прямой логической зависимости:
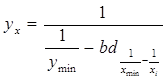
Для вычисления параметра  , составления уравнения однофакторной зависимости и дальнейшего анализа этой зависимости заполним таблицу 5. , составления уравнения однофакторной зависимости и дальнейшего анализа этой зависимости заполним таблицу 5.
Таблица 4.6
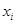 |
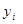 |
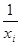 |
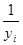 |
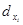 |
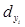 |
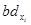 |
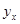 |
| 1,0 |
466 |
1,00000 |
0,00215 |
0,00000 |
0,00000 |
0,00000 |
466,00000 |
| 1,0 |
549 |
1,00000 |
0,00182 |
0,00000 |
0,00032 |
0,00000 |
466,00000 |
| 1,0 |
978 |
1,00000 |
0,00102 |
0,00000 |
0,00112 |
0,00000 |
466,00000 |
| 4,0 |
495 |
0,25000 |
0,00202 |
0,75000 |
0,00013 |
0,00039 |
570,13230 |
| 4,0 |
723 |
0,25000 |
0,00138 |
0,75000 |
0,00076 |
0,00039 |
570,13230 |
| 4,0 |
681 |
0,25000 |
0,00147 |
0,75000 |
0,00068 |
0,00039 |
570,13230 |
| 4,5 |
619 |
0,22222 |
0,00162 |
0,77778 |
0,00053 |
0,00041 |
574,89026 |
| 4,5 |
1049 |
0,22222 |
0,00095 |
0,77778 |
0,00119 |
0,00041 |
574,89026 |
| 4,5 |
1033 |
0,22222 |
0,00097 |
0,77778 |
0,00118 |
0,00041 |
574,89026 |
| 5,0 |
163 |
0,20000 |
0,00613 |
0,80000 |
-0,00399 |
0,00042 |
578,75418 |
| 5,0 |
182 |
0,20000 |
0,00549 |
0,80000 |
-0,00335 |
0,00042 |
578,75418 |
| 5,0 |
890 |
0,20000 |
0,00112 |
0,80000 |
0,00102 |
0,00042 |
578,75418 |
| 5,0 |
1522 |
0,20000 |
0,00066 |
0,80000 |
0,00149 |
0,00042 |
578,75418 |
| 5,0 |
1194 |
0,20000 |
0,00084 |
0,80000 |
0,00131 |
0,00042 |
578,75418 |
| 5,5 |
987 |
0,18182 |
0,00101 |
0,81818 |
0,00113 |
0,00043 |
581,95443 |
| 6,0 |
764 |
0,16667 |
0,00131 |
0,83333 |
0,00084 |
0,00044 |
584,64846 |
| 6,0 |
1373 |
0,16667 |
0,00073 |
0,83333 |
0,00142 |
0,00044 |
584,64846 |
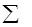 |
11,06818 |
0,00578 |
Примечание. Предпоследний и последний столбцы таблицы 4.6 заполняются после отыскания параметра уравнения зависимости  и составления самого уравнения зависимости. и составления самого уравнения зависимости.
В рассматриваемом примере параметр  , при , при 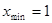 и и 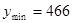 вычисляется по формуле: вычисляется по формуле:
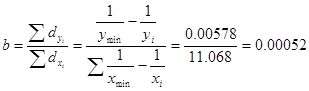
В рассматриваемом примере окончательный вид уравнения зависимости находим по формуле:
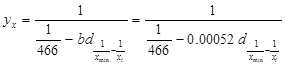
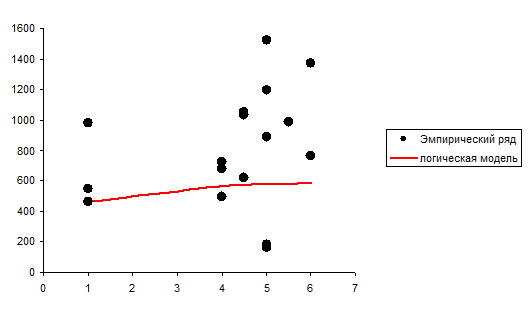
Отобразим эмпирические и теоретические значения результативного признака на графике (рисунок 6).
Рисунок 6
Информация для расчета коэффициента детерминации в типовой задаче в полном объеме представлена в таблице 4.7.
Таблица 4.7
 |
 |
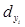 |
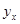 |
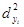 |
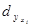 |
(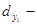 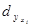 ) ) |
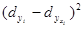 |
| 1,0 |
466 |
0,000 |
466,00 |
0,0000000 |
0,0000000 |
0,0000000 |
0,0000000 |
| 1,0 |
549 |
0,000 |
466,00 |
0,0000001 |
0,0000000 |
0,0003244 |
0,0000001 |
| 1,0 |
978 |
0,001 |
466,00 |
0,0000013 |
0,0000000 |
0,0011234 |
0,0000013 |
| 4,0 |
495 |
0,000 |
570,13 |
0,0000000 |
0,0003919 |
-0,0002662 |
0,0000001 |
| 4,0 |
723 |
0,001 |
570,13 |
0,0000006 |
0,0003919 |
0,0003709 |
0,0000001 |
| 4,0 |
681 |
0,001 |
570,13 |
0,0000005 |
0,0003919 |
0,0002856 |
0,0000001 |
| 4,5 |
619 |
0,001 |
574,89 |
0,0000003 |
0,0004065 |
0,0001240 |
0,0000000 |
| 4,5 |
1049 |
0,001 |
574,89 |
0,0000014 |
0,0004065 |
0,0007862 |
0,0000006 |
| 4,5 |
1033 |
0,001 |
574,89 |
0,0000014 |
0,0004065 |
0,0007714 |
0,0000006 |
| 5,0 |
163 |
-0,004 |
578,75 |
0,0000159 |
0,0004181 |
-0,0044071 |
0,0000194 |
| 5,0 |
182 |
-0,003 |
578,75 |
0,0000112 |
0,0004181 |
-0,0037667 |
0,0000142 |
| 5,0 |
890 |
0,001 |
578,75 |
0,0000010 |
0,0004181 |
0,0006043 |
0,0000004 |
| 5,0 |
1522 |
0,001 |
578,75 |
0,0000022 |
0,0004181 |
0,0010708 |
0,0000011 |
| 5,0 |
1194 |
0,001 |
578,75 |
0,0000017 |
0,0004181 |
0,0008903 |
0,0000008 |
| 5,5 |
987 |
0,001 |
581,95 |
0,0000013 |
0,0004276 |
0,0007052 |
0,0000005 |
| 6,0 |
764 |
0,001 |
584,65 |
0,0000007 |
0,0004355 |
0,0004015 |
0,0000002 |
| 6,0 |
1373 |
0,001 |
584,65 |
0,0000020 |
0,0004355 |
0,0009821 |
0,0000010 |
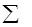 |
0,006 |
0,0000416 |
0,0000404 |
По данным таблицы 4.7 коэффициент детерминации составит:
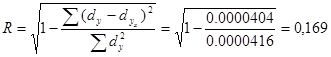
Сравним коэффициенты детерминации по трем моделям
Таблица 4.8
| Тип трендовой модели |
Уравнения зависимостей |
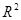 |
| Линейная |
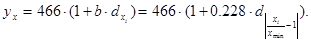 |
0,477 |
| Логарифмическая |
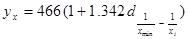 |
0,682 |
| Логическая |
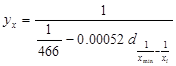 |
0,028 |
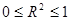 Чем слабее линейная связь между X и Y, тем R2 ближе к нулю, и чем эта связь значительнее, тем ближе R2 к единице. Чем слабее линейная связь между X и Y, тем R2 ближе к нулю, и чем эта связь значительнее, тем ближе R2 к единице.
Вывод: Анализируя результаты представленные в таблице 4.8 можно прийти к выводу что из представленных трендовых моделей, логарифмическая модель является наиболее адекватной.
5 Стимулирование и мотивация как функции управления
1. Задача стимулирования для одноэлементной системы.
Руководитель поручает рабочему производство продукции, используя следующую систему стимулирования: 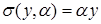 , где α – ставка оплаты единицы произведенной агентом продукции. Цена, по которой центр продаёт продукцию, p=1000 руб. Затраты агента, выраженные в денежной форме: , где α – ставка оплаты единицы произведенной агентом продукции. Цена, по которой центр продаёт продукцию, p=1000 руб. Затраты агента, выраженные в денежной форме: 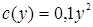 Определить параметр системы стимулирования α. Определить параметр системы стимулирования α.
Решение:
Запишем целевую функцию центра:
(3.1.1)
и целевую функцию агента:
(3.1.2)
Задача стимулирования формулируется:
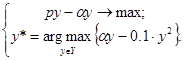 (3.1.3) (3.1.3)
(3.1.4)
Данная задача решается в 2 этапа. На первом этапе из выражения (3.1.4) определяется реакция агента как аналитическая зависимость от параметра системы стимулирования центра α . На втором этапе полученная аналитическая зависимость подставляется в формулу (3.1.3), получается задача безусловной оптимизации. Решая эту задачу, определим параметр системы стимулирования α.
Первый этап. Найдем реакцию агента из решения оптимизационной задачи (3.1.4). Для этого продифференцируем выражение (3.1.4) по y и приравняем к нулю:
Решая уравнение, определим реакцию агента:
Второй этап. Подставим реакцию агента в целевую функцию (3.1.3):
Вычислим первую производную и приравняем к нулю:
Решая уравнение, определим параметр α:
Ответ: параметр системы стимулирования равен 500.
2. Задача стимулирования для многоэлементной системы со слабосвязанными агентами.
Руководитель поручает работу бригаде, состоящей из двух рабочих. Центр использует пропорциональную систему стимулирования: 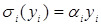 , где , где 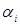 – ставка оплаты единицы произведенной i-м агентом продукции. Известна функция затрат каждого агента: – ставка оплаты единицы произведенной i-м агентом продукции. Известна функция затрат каждого агента: 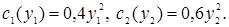
Рыночная цена, по которой продается продукция р=1000 руб., фонд заработной платы бригады R=20000 руб. Определить параметры системы стимулирования 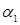 и и 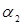 . .
Решение
Сформулируем задачу стимулирования:
(3.2.1)
(3.2.2)
(3.2.3)
(3.2.4)
Первый этап. Из выражения (3.2.2) и (3.2.3) определим реакцию агентов.
Для нахождения экстремума функции одной переменной продифференцируем функции и приравняем к нулю:

Из решения уравнений следует:

Второй этап. Подставив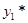 и и  в выражение для целевой функции центра (3.2.1) и ограничение (3.2.4), получим задачу на условный экстремум: в выражение для целевой функции центра (3.2.1) и ограничение (3.2.4), получим задачу на условный экстремум:

Для ее решения применим метод множителей Лагранжа. Запишем функцию Лагранжа:

Найдём частные производные от функции Лагранжа по неизвестным 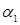 , ,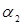 и и 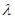 :(3.2.5) :(3.2.5)

(3.2.6)
(3.2.7)
Выразим из (3.2.5) и (3.2.6) неизвестные 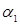 , ,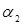 : :

Получилось, что параметры функций стимулирования для обоих агентов одинаковы. Из ограничения (3.2.7) определяем параметр системы стимулирования:

  Ответ: Параметры системы стимулирования и равны между собой и равны 30,98. Ответ: Параметры системы стимулирования и равны между собой и равны 30,98.
3. Задача стимулирования для многоэлементной системы с сильносвязанными агентами.
Руководитель (центр) поручает работу бригаде, состоящей из 2 рабочих. Рабочие (агенты) изготавливают однородную продукцию объёмом yi , которую центр продаёт по цене p=1500. Центр использует пропорциональную систему стимулирования
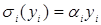 , ,
где 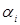 – ставка оплаты единицы продукции. – ставка оплаты единицы продукции.
Затраты агентов определяются соответственно:
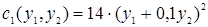 , ,
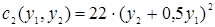 . .
Фонд заработной платы, которым располагает центр составляет R=37000 денежных единиц. Определить параметры системы стимулирования 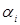 . .
Решение
Запишем целевую функцию центра:

(3.3.1)
и целевые функции агентов:

(3.3.2)
 (3.3.3) (3.3.3)
Сформулируем задачу стимулирования:
 (3.3.4) (3.3.4)
(3.3.5)
(3.3.6)
Первый этап. Найдем реакцию первого агента из решения оптимизационной задачи. Для этого продифференцируем целевую функцию агента по 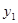 и приравняем к нулю: и приравняем к нулю:

Решая уравнение, определим реакцию первого агента:

Аналогично найдём реакцию второго агента:

Решив систему уравнений:

относительно y1 и y2получим реакции агентов:

Второй этап. Подставим реакции агентов в целевую функцию центра:

Продифференцировав это выражение по 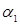 , ,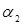 и приравняв нулю, получим систему уравнений: и приравняв нулю, получим систему уравнений:

  Решив полученную систему уравнений, определим параметры системы Решив полученную систему уравнений, определим параметры системы
стимулирования и
Ответ: параметры системы стимулирования 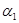 и и 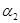 равны 645,83 и 961,01 соответственно. равны 645,83 и 961,01 соответственно.
|