1.4. Решить задачу с использованием графического метода
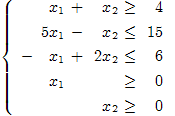 , ,

Решение
1) Многоугольник решений.
Найдем точки, через которые пройдут предельные прямые [1, c. 20].
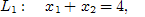 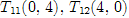
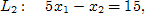 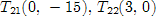
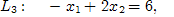 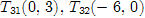
Строим многоугольник решений.
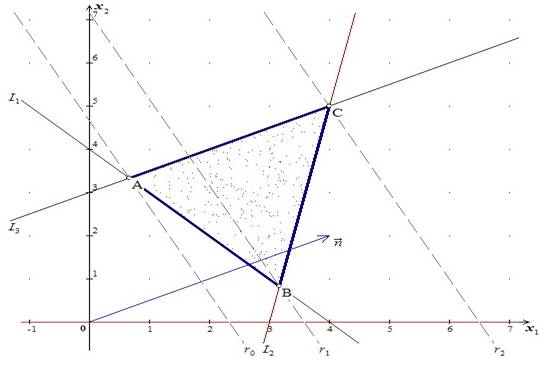
2) Оптимальные точки.
Строим вектор нормали, координаты которого 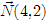 . Передвигая линию уровня r в направлении нормали, находим, что Zmin
находится в точке A, Zmax
– в точке C. . Передвигая линию уровня r в направлении нормали, находим, что Zmin
находится в точке A, Zmax
– в точке C.
3) Вычисление координат экстремумов.
Точка A – пересечение прямых L1
и L3
:
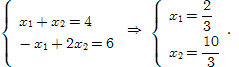
Точка C – пересечение прямых L2
и L3
:
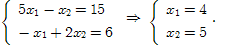
4) Подсчет оптимальных значений.
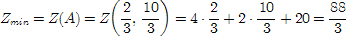
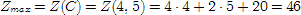
Ответ: 88/3, 46.
2.4. Для изготовления 2-х видов продукции P1
и P2
используется 3 вида ресурсов R1
, R2
, R3
. Запасы ресурсов, нормы их использования и прибыль от реализации единицы продукции приведены в таблице. Найти план производства продукции, которой бы при заданных условиях обеспечивал наибольшую прибыль.
Задачу решить графическим способом и симплексным методом, составить двойственную задачу к исходной и выписать ее оптимальный план из последней симплекс-таблицы решенной исходной задачи.
 Pi Pi
Ri
|
Р1
|
Р2
|
Запасы
ресурсов
|
| R1
|
2 |
5 |
80 |
| R2
|
4 |
3 |
91 |
| R3
|
1 |
4 |
68 |
| Прибыль |
15 |
12 |
Решение
Составим математическую модель задачи. Искомый выпуск продукции P1
обозначим через x1
, продукции P2
– через x2
. Поскольку есть ограничение на выделенные ресурсы каждого вида, переменные x1
, x2
должны удовлетворять такой системе неравенств:
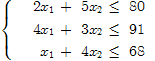
Общая стоимость продукции при этом составляет: z = 15x1
+ 12x2
.
По своему экономическому содержанию переменные x1
, x2
больше 0.
Следовательно, приходим к математической задаче: среди всех неотрицательных решений системы неравенств нужно найти такое, при котором функция z примет максимальное значение.
Решим задачу графическим способом.
1) Многоугольник решений
Найдем точки, через которые пройдут предельные прямые [1, c. 20].
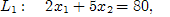 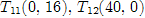
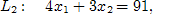 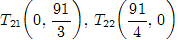
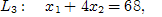 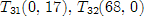
Строим многоугольник решений.
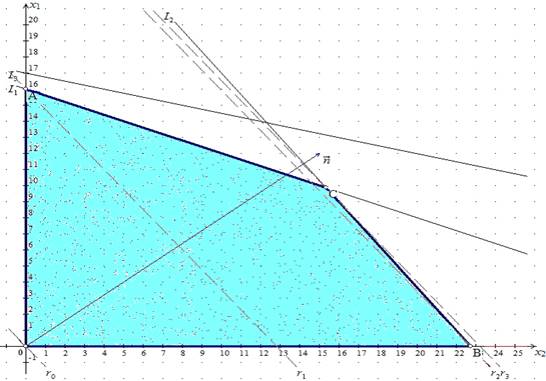
2) Оптимальные точки.
Строим вектор нормали, координаты которого 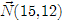 . Передвигая линию уровня r в направлении нормали, находим, что Fmin
находится в точке O, Fmax
- в точке C. . Передвигая линию уровня r в направлении нормали, находим, что Fmin
находится в точке O, Fmax
- в точке C.
3) Вычисление координат экстремумов.
Точка C - пересечение прямых L1
и L2
:
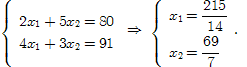
4) Подсчет оптимальных значений.
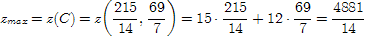
Ответ: 4881/14.
Решим задачу ЛП симплекс-методом [1, c. 30].
Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем к ограничениям-уравнениям. Введем дополнительные 3 переменные – x3
, x4
, x5
, в результате чего ограничения запишутся в виде уравнений:
Реклама

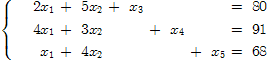
Построим начальную симплекс-таблицу, где Q – неотрицательное отношение столбца плана к ключевому столбцу.
| № |
Базис |
Cб
|
План |
15 |
12 |
0 |
0 |
0 |
Q |
| x1
|
x2
|
x3
|
x4
|
x5
|
| 1 |
x3
|
0 |
80 |
2 |
5 |
1 |
0 |
0 |
40 |
| 2 |
x4
|
0 |
91 |
4 |
3 |
0 |
1 |
0 |
91/4 |
| 3 |
x5
|
0 |
68 |
1 |
4 |
0 |
0 |
1 |
68 |
| 4 |
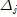 |
0 |
-15 |
-12 |
0 |
0 |
0 |
– |
Cтолбик 1 есть ключевым, поскольку он содержит минимальный отрицательный элемент 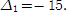
Строка 2 есть ключевой, поскольку в ней минимальное Q2
=91/4.
Ключевой элемент находится на их пересечении и равный числу 4.
Вместо вектора x4
, который выводим из базиса, вводим вектор x1
.
Делим ключевую строку на ключевой элемент 4.
Умножаем его на 15 и добавляем к 4 строке.
Умножаем его на -2 и добавляем к 1 строке.
Умножаем его на -1 и добавляем к 3 строке.
Получим следующую симплекс-таблицу.
| № |
Базис |
Cб
|
План |
15 |
12 |
0 |
0 |
0 |
Q |
| x1
|
x2
|
x3
|
x4
|
x5
|
| 1 |
x3
|
0 |
69/2 |
0 |
7/2 |
1 |
-1/2 |
0 |
69/7 |
| 2 |
x1
|
15 |
91/4 |
1 |
3/4 |
0 |
1/4 |
0 |
91/3 |
| 3 |
x5
|
0 |
181/4 |
0 |
13/4 |
0 |
-1/4 |
1 |
181/13 |
| 4 |
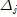 |
1365/4 |
0 |
-3/4 |
0 |
15/4 |
0 |
– |
Cтолбик 2 есть ключевым, поскольку он содержит минимальный отрицательный элемент 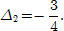
Строка 1 есть ключевой, поскольку в ней минимальное Q1
=69/7.
Ключевой элемент находится на их пересечении и равный числу 7/2.
Вместо вектора x3
, который выводим из базиса, вводим вектор x2
.
Делим ключевую строку на ключевой элемент 7/2.
Умножаем его на 3/4 и добавляем к 4 строке.
Умножаем его на -3/4 и добавляем к 2 строке.
Умножаем его на -13/4 и добавляем к 3 строке.
Получим окончательную симплекс-таблицу.
| № |
Базис |
Cб
|
План |
15 |
12 |
0 |
0 |
0 |
| x1
|
x2
|
x3
|
x4
|
x5
|
| 1 |
x2
|
12 |
69/7 |
0 |
1 |
2/7 |
-1/7 |
0 |
| 2 |
x1
|
15 |
215/14 |
1 |
0 |
-3/14 |
5/14 |
0 |
| 3 |
x5
|
0 |
185/14 |
0 |
0 |
-13/14 |
3/14 |
1 |
| 4 |
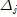 |
4881/14 |
0 |
0 |
3/14 |
51/14 |
0 |
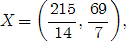 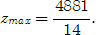
Составим двойственную задачу к данной [1, c. 88]. Ее коэффициенты складываются с исходной путем транспонирования. Систему ограничений составят коэффициенты оптимизирующей функции. Коэффициентами оптимизирующей функции z будут свободные члены исходной системы. Знаки неравенств изменятся на противоположные. Оптимизирующая функция – минимум функции. Двойственная задача будет заключаться в том, чтобы составить такой план производства, при котором затраты ресурсов будут минимальными.
Следовательно, через y1
обозначим стоимость единицы ресурса 1 вида или А1
, y2
– стоимость единицы А2
, y3
– стоимость единицы А3
. Тогда 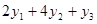 – стоимость продукции Р1
, которая не может быть дешевле чем 15 у.д.е. (условных денежных единиц), то есть первое неравенство: – стоимость продукции Р1
, которая не может быть дешевле чем 15 у.д.е. (условных денежных единиц), то есть первое неравенство: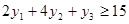 . Аналогично . Аналогично 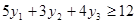 . .
Общие потери ресурсов выражаются оптимизирующей функцией:
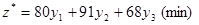 при при 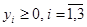 . .
Следовательно, математически это запишется так:
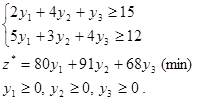
С 4 рядка последней симплекс-таблицы виписываем оптимальный план, где y1
=x3
, y2
=x4
, y3
=x5
, тоесть 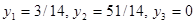 . .
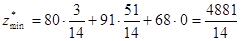 . .
Значение 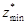 отвечает значению 4881/14, что находится в 0 рядке планового столбика. отвечает значению 4881/14, что находится в 0 рядке планового столбика.
С экономической точки зрения нулевое значение переменной у3
значит, что для минимальных издержек стоимость ресурсів R3
должна равняться 0.
Реклама

Таким образом, продукции P1
и P2
нужно производить 215/14 и 69/14 ед. соответственно. Максимальная прибыль при этом составит 4881/14 у.д.е.
Ответ: 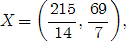 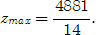
3.4. Найти оптимальный план транспортной задачи.
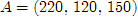
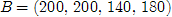
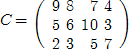
Решение
Запишем условие задачи в экономическом виде на основании таблицы, где заданы пункты отправления и назначения, запасы и потребности [1, c. 135].
| Пункты отправления |
Пункты назначения |
Запасы |
| B1
|
B2
|
B3
|
B4
|
| A1
|
9 |
8 |
7 |
4 |
220 |
| A2
|
5 |
6 |
10 |
3 |
120 |
| A3
|
2 |
3 |
5 |
7 |
150 |
| Потребности |
200 |
200 |
140 |
180 |
720\490 |
Поскольку запасы и потребности не совпадают, имеем задачу с неправильным балансом или открытую, следовательно введем фиктивный пункт отправления с количеством 230 единиц груза.
1) Диагональный метод
Найдем опорный план диагональным методом [1, c. 140].
B
A
|
1 |
2 |
3 |
4 |
a |
| 200 |
200 |
140 |
180 |
| 1 |
220 |
9 |
8 |
7 |
4 |
0 |
| 200 |
20 |
– |
0 |
+ |
| 2 |
120 |
5 |
6 |
10 |
3 |
–2 |
| 120 |
| 3 |
150 |
2 |
3 |
5 |
7 |
–5 |
| 60 |
+ |
90 |
– |
| 4 |
230 |
0 |
0 |
0 |
0 |
–10 |
| 50 |
+ |
180 |
– |
| b |
9 |
8 |
10 |
10 |
Стоимость начального плана перевозки:
z0
= 200 · 9+20 · 8+120 · 6+60 · 3+90 · 5+50 · 0+180 · 0 = 3310.
Для базисных клеток система потенциалов такая:
a1
+b1
=9; a1
+b2
=8;
a2
+b2
=6;
a3
+b2
=3; a3
+b3
=5;
a4
+b3
=0; a4
+b4
=0.
Поскольку количество переменных меньше, чем уравнений, то положим: a1
=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1
+b3
=0+10=10 > 7 [3]; a1
+b4
=0+10=10 > 4 [6];
a2
+b1
=–2+9=7 > 5 [2]; a2
+b3
=–2+10=8 ≤ 10; a2
+b4
=–2+10=8 > 3 [5];
a3
+b1
=–5+9=4 > 2 [2]; a3
+b4
=–5+10=5 ≤ 7;
a4
+b1
=–10+9=–1 ≤ 0; a4
+b2
=–10+8=–2 ≤ 0;
Для клетки A1
B4
(из тех, что не выполняется условие оптимальности) разница потенциалов наибольшая, потому для нее делаем цикл пересчета на минимальную величину отрицательных вершин: min(20, 90, 180)=20.
Переходим к следующей итерации.
B
A
|
1 |
2 |
3 |
4 |
a |
| 200 |
200 |
140 |
180 |
| 1 |
220 |
9 |
8 |
7 |
4 |
0 |
| 200 |
– |
20 |
+ |
| 2 |
120 |
5 |
6 |
10 |
3 |
4 |
| 0 |
+ |
120 |
– |
| 3 |
150 |
2 |
3 |
5 |
7 |
1 |
| 80 |
+ |
70 |
– |
| 4 |
230 |
0 |
0 |
0 |
0 |
–4 |
| 70 |
+ |
160 |
– |
| b |
9 |
2 |
4 |
4 |
Стоимость 1 плана перевозки:
z1
= 200 · 9+20 · 4+120 · 6+80 · 3+70 · 5+70 · 0+160 · 0 = 3190.
Для базисных клеток система потенциалов такая:
a1
+b1
=9; a1
+b4
=4;
a2
+b2
=6;
a3
+b2
=3; a3
+b3
=5;
a4
+b3
=0; a4
+b4
=0.
Поскольку количество переменных меньше, чем уравнений, то положим: a1
=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1
+b2
=0+2=2 ≤ 8; a1
+b3
=0+4=4 ≤ 7;
a2
+b1
=4+9=13 > 5 [8]; a2
+b3
=4+4=8 ≤ 10; a2
+b4
=4+4=8 > 3 [5];
a3
+b1
=1+9=10 > 2 [8]; a3
+b4
=1+4=5 ≤ 7;
a4
+b1
=–4+9=5 > 0 [5]; a4
+b2
=–4+2=–2 ≤ 0;
Для клетки A2
B1
(из тех, что не выполняется условие оптимальности) разница потенциалов наибольшая, потому для нее делаем цикл пересчета на минимальную величину отрицательных вершин: min(200, 160, 70, 120)=70.
Переходим к следующей итерации.
B
A
|
1 |
2 |
3 |
4 |
a |
| 200 |
200 |
140 |
180 |
| 1 |
220 |
9 |
8 |
7 |
4 |
0 |
| 130 |
– |
90 |
+ |
| 2 |
120 |
5 |
6 |
10 |
3 |
–4 |
| 70 |
+ |
50 |
– |
| 3 |
150 |
2 |
3 |
5 |
7 |
–7 |
| 150 |
| 4 |
230 |
0 |
0 |
0 |
0 |
–4 |
| 0 |
+ |
140 |
90 |
– |
| b |
9 |
10 |
4 |
4 |
Стоимость 2 плана перевозки:
z2
= 130 · 9+90 · 4+70 · 5+50 · 6+150 · 3+140 · 0+90 · 0 = 2630.
Для базисных клеток система потенциалов такая:
a1
+b1
=9; a1
+b4
=4;
a2
+b1
=5; a2
+b2
=6;
a3
+b2
=3;
a4
+b3
=0; a4
+b4
=0.
Поскольку количество переменных меньше, чем уравнений, то положим: a1
=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1
+b2
=0+10=10 > 8 [2]; a1
+b3
=0+4=4 ≤ 7;
a2
+b3
=–4+4=0 ≤ 10; a2
+b4
=–4+4=0 ≤ 3;
a3
+b1
=–7+9=2 ≤ 2; a3
+b3
=–7+4=–3 ≤ 5; a3
+b4
=–7+4=–3 ≤ 7;
a4
+b1
=–4+9=5 > 0 [5]; a4
+b2
=–4+10=6 > 0 [6];
Для клетки A4
B2
(из тех, что не выполняется условие оптимальности) разница потенциалов наибольшая, потому для нее делаем цикл пересчета на минимальную величину отрицательных вершин: min(50, 130, 90)=50.
Переходим к следующей итерации.
B
A
|
1 |
2 |
3 |
4 |
a |
| 200 |
200 |
140 |
180 |
| 1 |
220 |
9 |
8 |
7 |
4 |
0 |
| 80 |
– |
140 |
+ |
| 2 |
120 |
5 |
6 |
10 |
3 |
–4 |
| 120 |
| 3 |
150 |
2 |
3 |
5 |
7 |
–1 |
| 0 |
+ |
150 |
– |
| 4 |
230 |
0 |
0 |
0 |
0 |
–4 |
| 50 |
+ |
140 |
40 |
– |
| b |
9 |
4 |
4 |
4 |
Стоимость 3 плана перевозки:
z3
= 80 · 9+140 · 4+120 · 5+150 · 3+50 · 0+140 · 0+40 · 0 = 2330.
Для базисных клеток система потенциалов такая:
a1
+b1
=9; a1
+b4
=4;
a2
+b1
=5;
a3
+b2
=3;
a4
+b2
=0; a4
+b3
=0; a4
+b4
=0.
Поскольку количество переменных меньше, чем уравнений, то положим: a1
=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1
+b2
=0+4=4 ≤ 8; a1
+b3
=0+4=4 ≤ 7;
a2
+b2
=–4+4=0 ≤ 6; a2
+b3
=–4+4=0 ≤ 10; a2
+b4
=–4+4=0 ≤ 3;
a3
+b1
=–1+9=8 > 2 [6]; a3
+b3
=–1+4=3 ≤ 5; a3
+b4
=–1+4=3 ≤ 7;
a4
+b1
=–4+9=5 > 0 [5];
Для клетки A3
B1
(из тех, что не выполняется условие оптимальности) разница потенциалов наибольшая, потому для нее делаем цикл пересчета на минимальную величину отрицательных вершин: min(80, 40, 150)=40.
Переходим к следующей итерации.
B
A
|
1 |
2 |
3 |
4 |
a |
| 200 |
200 |
140 |
180 |
| 1 |
220 |
9 |
8 |
7 |
4 |
0 |
| 40 |
– |
0 |
+ |
180 |
| 2 |
120 |
5 |
6 |
10 |
3 |
–4 |
| 120 |
| 3 |
150 |
2 |
3 |
5 |
7 |
–7 |
| 40 |
+ |
110 |
– |
| 4 |
230 |
0 |
0 |
0 |
0 |
–10 |
| 90 |
+ |
140 |
– |
| b |
9 |
10 |
10 |
4 |
Стоимость 4 плана перевозки:
z4
= 40 · 9+180 · 4+120 · 5+40 · 2+110 · 3+90 · 0+140 · 0 = 2090.
Для базисных клеток система потенциалов такая:
a1
+b1
=9; a1
+b4
=4;
a2
+b1
=5;
a3
+b1
=2; a3
+b2
=3;
a4
+b2
=0; a4
+b3
=0;
Поскольку количество переменных меньше, чем уравнений, то положим: a1
=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1
+b2
=0+10=10 > 8 [2]; a1
+b3
=0+10=10 > 7 [3];
a2
+b2
=–4+10=6 ≤ 6; a2
+b3
=–4+10=6 ≤ 10; a2
+b4
=–4+4=0 ≤ 3;
a3
+b3
=–7+10=3 ≤ 5; a3
+b4
=–7+4=–3 ≤ 7;
a4
+b1
=–10+9=–1 ≤ 0; a4
+b4
=–10+4=–6 ≤ 0;
Для клетки A1
B3
(из тех, что не выполняется условие оптимальности) разница потенциалов наибольшая, потому для нее делаем цикл пересчета на минимальную величину отрицательных вершин: min(40, 110, 140)=40.
Переходим к следующей итерации.
B
A
|
1 |
2 |
3 |
4 |
a |
| 200 |
200 |
140 |
180 |
| 1 |
220 |
9 |
8 |
7 |
4 |
0 |
| 40 |
180 |
| 2 |
120 |
5 |
6 |
10 |
3 |
–1 |
| 120 |
| 3 |
150 |
2 |
3 |
5 |
7 |
–4 |
| 80 |
70 |
| 4 |
230 |
0 |
0 |
0 |
0 |
–7 |
| 130 |
100 |
| b |
6 |
7 |
7 |
4 |
Стоимость 5 плана перевозки:
z5
= 40 · 7+180 · 4+120 · 5+80 · 2+70 · 3+130 · 0+100 · 0 = 1970.
Для базисных клеток система потенциалов такая:
a1
+b3
=7; a1
+b4
=4;
a2
+b1
=5;
a3
+b1
=2; a3
+b2
=3;
a4
+b2
=0; a4
+b3
=0;
Поскольку количество переменных меньше, чем уравнений, то положим: a1
=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1
+b1
=0+6=6 ≤ 9; a1
+b2
=0+7=7 ≤ 8;
a2
+b2
=–1+7=6 ≤ 6; a2
+b3
=–1+7=6 ≤ 10; a2
+b4
=–1+4=3 ≤ 3;
a3
+b3
=–4+7=3 ≤ 5; a3
+b4
=–4+4=0 ≤ 7;
a4
+b1
=–7+6=–1 ≤ 0; a4
+b4
=–7+4=–3 ≤ 0;
Условие оптимальности выполняется для всех клеток, следовательно последний план является оптимальным. Его стоимость составляет 1970 у.е. Следует заметить, что потребители не дополучат 230 ед. груза.
2) Метод минимальной стоимости
Найдем опорный план методом минимальной стоимости [1, c. 142].
B
A
|
1 |
2 |
3 |
4 |
a |
| 200 |
200 |
140 |
180 |
| 1 |
220 |
9 |
8 |
7 |
4 |
0 |
| 40 |
180 |
| 2 |
120 |
5 |
6 |
10 |
3 |
–1 |
| 120 |
| 3 |
150 |
2 |
3 |
5 |
7 |
–4 |
| 80 |
70 |
| 4 |
230 |
0 |
0 |
0 |
0 |
–7 |
| 130 |
100 |
| b |
6 |
7 |
7 |
4 |
Стоимость начального плана перевозки:
z0
= 40 · 7+180 · 4+120 · 5+80 · 2+70 · 3+130 · 0+100 · 0 = 1970.
Для базисных клеток система потенциалов такая:
a1
+b3
=7; a1
+b4
=4;
a2
+b1
=5;
a3
+b1
=2; a3
+b2
=3;
a4
+b2
=0; a4
+b3
=0;
Поскольку количество переменных меньше, чем уравнений, то положим: a1
=0. Проверяем условие оптимальности для свободных клеток: a + b ≤ c
a1
+b1
=0+6=6 ≤ 9; a1
+b2
=0+7=7 ≤ 8;
a2
+b2
=–1+7=6 ≤ 6; a2
+b3
=–1+7=6 ≤ 10; a2
+b4
=–1+4=3 ≤ 3;
a3
+b3
=–4+7=3 ≤ 5; a3
+b4
=–4+4=0 ≤ 7;
a4
+b1
=–7+6=–1 ≤ 0; a4
+b4
=–7+4=–3 ≤ 0;
Условие оптимальности выполняется для всех клеток, следовательно последний план является оптимальным. Его стоимость составляет 1970 у.е. Следует заметить, что потребители не дополучат 230 ед. груза.
Также отмечаем совпадение решений двумя методами.
Ответ: 1970.
Література
1. Акулич И. Л. Математическое программирование в примерах и задачах. М.: Высшая школа, 1986. – 319 с.
2. Костевич Л. С. Математическое программирование. Мн.: Новое знание, 2003. – 424 с.
|