| Статья посвящена исследованию доказательства теоремы Ферма в общем виде. Показано, что кроме уравнения второй степени уравнения Ферма не содержат других решений в целых числах. Предложено к рассмотрению
4 метода доказательства теоремы при целых x, y. Проблему доказательства теоремы Ферма следует считать закрытой. |
|
Более 350 лет профессиональные математики и любители пытаются доказать теорему Ферма. Однако до настоящнго времени нет общепризнанного доказательства. Тем не менее, интерес к загадочной теореме не угасает и до настоящего времени остается высоким.
В настоящей статье предлагается к рассмотрению простой метод доказательства, основанный на разделении числового множества yn
+
xn
=
zn
(1)
на два подмножества, из которых первое содержит только те x
и y
для всех показателей степени n
,
которые могут содержатьрешения уравнения (1) в целых числах x
,
y
,
z
,
а второе подмножество содержит только нецелые решения.
Отделить друг от друга упомянутые подмножества представляется возможным путем разложения уравнения (1) на составные части по биному Ньютона и составления на их основе уравнения с учетом принятых ограничений для поиска целых решений. Для этого представим уравнение (1) в виде, удобном для разложения :
(x - a)n
+ xn
–(x+b)n
= 0 (2)
Здесь: x
– переменное число, а <
x
–
целое число; n
–
целое число, показатель степени; b
–
целое или нецелое число, в зависимости от соотношения x
,
a
,
и n
.
Сущность доказательства заключается в определении подходящих значений x,y,zдля удовлетворения уравнений ( 1 )
и ( 2 )
методом последовательных приближений. Задача решается применительно к 450
сектору I квадранта в плоскостных координатах (x,y), т.к. из-за недостатка информации координата z равна 0. Полученные результаты могут быть распространены на остальные 7 секторов плоскости(x,y), определяя тем самым область распространения условий теоремы Ферма.
Итак, применяя формулу бинома Ньютона к выражению (2), получим:
(x–a)n
+ xn
= 2xn
- nxn-1
a + cn
2
xn-2
a2
- cn
3
xn-3
a3
...... +
an
(x+b)n
= xn
+nxn-1
b + cn
2
xn-2
b2
+ cn
3
xn-3
b3
.......+bn
D = xn
- nxn-1
(a+b) + cn
2
xn-2
(a2
-b2
) - cn
3
xn-3
(a3
+b3
)..+(an
+
bn
) =0
(3)
Назовем выражение (3) основным уравнением в поисках целых решений уравнения (2). Подходящие значения x
,
y
=(
x
–
a
),
z
=(
x
+
b
),
удовлетворяющие уравнениям (1) и (2), будем искать при условии a
=
b
=1.
Обоснование принятых допущений (ограничений) изложено ниже. Полагая a =
b
, уравнение (3) преобразуем к виду:
xn
- 2nxn-1
a - 2cn
3
xn-3
a3
- 2cn
5
xn-5
a5
- ... (an
+
an
)=0
(4)
Реклама

ОбозначимчерезP(a,n) = 2cn
3
xn-3
a3
+ 2cn
5
xn-5
a5
+...
(
an
+
an
)
-
добавку после первых двух членов уравнения (4). Тогда уравнение (4) примет вид:
xn
- 2nxn-1
a - P(a,n) = 0
Разделив все члены уравнения на xn
-1
, получим выражение для искомого x
x=2
na
+
P
(
a,n
)/
xn
-1
,
гдеP(a,n)/xn-1
³
0
(5)
При a
=
b
= 1
выражение (5)
примет вид:
x=2n+P(
1
,n)/xn-1
(6)
Подходящие значения y=x-1 и z=x+1 определяются через известный х. Из формул (5) и (6) становится ясным, что при n>2 согласование левых и правых частей уравнений (1) и (2) возможно только при учете добавки P
(1
,
n
)/
xn
-1
.
Исходя из изложенного, целые числа х
и у
из теоремы Ферма следует однозначно отнести ко второму подмножествуyn
+
xn
=
zn
Ниже, в таблице приведены результаты расчетов согласования для n=2,3,4 и 5.
| n |
x
|
y=x-1
|
z=x+1
|
xn
|
yn
|
xn
+ yn
|
zn
|
D
%
|
| 2 |
4 |
3 |
5 |
16 |
9 |
25 |
25 |
- |
| 3 |
6,055 |
5,055 |
7,055 |
221 |
129 |
350 |
350 |
- |
| 4 |
8,125 |
7,125 |
9,125 |
4350 |
2540 |
6890 |
6890 |
- |
| 5 |
10,200 |
9,200 |
11,200 |
107000 |
66000 |
173000 |
175000 |
1,25 |
На основании изложенного можно сделать следующие предварительные выводы:
1. Согласование левых и правых частей уравнений (1) и (2) невозможно без учета добавки P
(
a
,
n
)/
xn
-1
.
2. Если уравнение yn
+
xn
=
zn
с учетом добавки P
(
a
,
n
)
выразить в числовых отрезках и спроектировать на плоскость (х,у), то на ней при n>2 образуется остроугольный треугольник, все стороны которого при a=b=1 выражены нецелыми числами: х=2n+P(1,
n
)/хn
-1
; у=2n-1+ P(1,
n
)/хn
-1
; z=2n+1+ P(1,
n
)/хn
-1
, что находит подтверждение при следующем рассмотрении добавки P(1,
n
)/хn
-1
.
Для выяснения этого вопроса представим ее после сокращений в следующем виде
P(1,n)/
х
n-1
=
2cn
3
/x2
+ 2cn
5
/x4
+2cn
7
/x6
...
(
1
+
1
)
/
xn
-1
В числителе каждого члена разложения представлены сочетанияcn
k
, распределение которых симметрично, наподобие гаусовскому, относительно центра (
n+1)/2
. В знаменателе функция x
2
, возрастающая с каждым членом по квадратичному закону.
Первый член разложения, из-за малости x
2
имеет наибольшую величину и может выражаться целым числом со значащими цифрами после запятой (для n=15 – 1,1…; для n=25 – 1,8…; и т.п.). Последний член имеет наименьшую величину из-за большого знаменателяxn
-1
(для n=3 – 2/62
; для n=15– порядка 2/3014
; для n=25– 2/5024
и т.п.)
Первая половина разложения по сумме значительно превышает вторую за счет резкого увеличения числителей. Все члены разложения второй половины меньше 1 за счет уменьшения числителей и дальнейшего возрастания знаменателей, и интенсовно уменьшаются по мере удаления от центра. В результате общая сумма разложения для n>14 (для n<=14 добавка <1) всегда будет определяться целыми числами со значащими цифрами после запятой, т.е. все эти числа будут нецелыми, что свидетельствует о достоверности и доказуемости теоремы Ферма.
Реклама

3. Известно, что уравнение второй степениy
2
+
x
2
=
z
2
решается в целых числах, а её проекцией на плоскость (х,у) является прямоугольный треугольник. Можно предположить, что для более высоких степеней n найдется прямоугольная проекция, при которой решение уравнения Ферма будет происходить при целых x
,
y
,
z
.
Такое предположение оправдано для степени n=3 в объемных прямоугольных координатах x
,
y
,
z
,
в которых для уравнения (
x
-2
a
)3
+(
x
-
a
)3
+
x
3
=(
x
+
b
)3
,
существуют целые числа 3,4,5,6 и им кратные, которые удовлетворяют условию 33
+43
+53
=63
.
Физически эти числа выражают сумму кубов в целых числах, по аналогии с n=2, где сумма квадратов означает сумму площадей. По сути мы получили новый вариант теоремы Ферма.
4. Искажения проекций (треугольников) по мере возрастания n обусловлены отражением на плоскости (х,у) несвойственных ей структур более высокого порядка. Отсюда можно заключить, что решения теоремы Ферма в целых числах связаны с наличием прямоугольных проекций, а при нецелых решениях- с искаженными проекциями в виде остроугольных треугольников.

Это подтверждается следующими математическими выкладками. Предварительно решим треугольник АВС из теоремы косинусов относительно cosC, где C –угол между сторонами а и b
сosC= (a2
+ b2
-c2
)/2ab. Подставим вместо сторон а,
b
и с
их аналоги из треугольных проекций при а = b =1:
а
→ x; b → y=x-1; c → z=x+1
, гдеx=2n+P(1
,n
)/xn-1
После выполнения операций преобразования получим:
cosCn
= 0,5-1,5/
xn
-1 (7)
По полученной формуле проведены расчеты
| n |
2 |
3 |
4 |
5 |
10 |
∞ |
| x-1 |
3 |
5.054 |
7.125 |
9.200 |
19.0.. |
∞ |
| cosC
|
0 |
0.202 |
0.289 |
0.337 |
0.421 |
0.5 |
| Co
|
90 |
78 |
73 |
70 |
65 |
60 |
Из которых следует :
- искажение треугольников при n>2 обусловлено изменением угла С от 90о
при n=2 до 60о
при n→
∞ при этом треугольники превращаются из прямоугольных в остроугольные и в пределе – в равносторонние.
- В остроугольных треугольниках нет целых решений уравнений Ферма т.к. их стороны сформированы нецелыми числами.
- Решение теоремы Ферма в целых числах присуще только прямоугольным проекциям на плоскость (х,у) числовых отрезков уравнений y
2
+
x
2
=
z
2
5. Второй сектор квадранта является аналогом первого- зеркальным отражением первого при y>x со всеми вытекающими из этого результатами.
6. В процессе проведения анализа по доказательству теоремы Ферма в общем виде получены 4 компактных метода доказательства теоремы при целых x, y, когда требуется показать , что при n>2 число z является нецелым.
Первый метод
доказательства следует из рассмотрения остроугольного треугольника, для которого Z
0
2
= x
2
+
y
2
–2
xycosc
.
Требуется доказать, что Z
0
является нецелым числом. В нем известны x и y – целые числа, а cosc
определен с учетом ограничений a=b=1. Он изменяется в пределах 0< cosc < 0,5 (см. ф-лу (7) и табл. на стр.3) и является функцией нецелого, иррационального числа х. Значит и соsc является также нецелым числом со множеством значащих цифр после запятой. Благодаря этому нецелым становится выражение 2
xycosc
,
что в свою очередь делает нецелым Z
0
2
и извлеченный из него квадратный корень Z
0.
В основу второго метода
также заложено рассмотрение остроугольного треугольника. Его Z
0
2
= x
2
+
y
2
–2
xycosc
всегда меньше соответствующего Z
п
2
= x
2
+
y
2
прямоугольного треугольника и числовой отрезок Z
0
2
находится внутри числового отрезкаZ
п
2
=x
2
+
y
2
.
Учитывая, что при принятых ограничениях y=x-1, т.е. отличается на единицу, то корень, извлеченный из Z
0
2
будет иметь нецелое значение, т.к. между числами x-1 и x нет других целых чисел.
Третий метод
основан на другом принципе. Его сущность заключается в следующем.
Для последовательности целых чисел 1,2,3,4 и т.д. составляется ряд их квадратов:
1 4 9 16 25 36 4964 81 100 121 144 169 196 и т.д.
2 4
6 8
10 12
14 16
18 20
22 24
26 и т.д.
Между числами первого ряда размещается нижний ряд, представляющий собой количество целых чисел (порядковых номеров), размещенных между двумя смежными квадратами чисел x и x+1. Эти целые (и нецелые) числа z1
не могут иметь при извлечении из них корней целых значений, т.к. находятся между числами, отличающимися на единицу, а будут иметь значения x+D, где D=z1
/Dx2
Учитывая, что при n>2 для остроугольных треугольников z0
2
всегда меньше zп
2
или соответствующего Dx2
в ряду квадратов, необходимо вставить числовой отрезок z0
2
в числовой отрезок Dx2
и убедиться, что извлеченный корень из числа z0
2
является нецелым числом.
Рассмотрим доказательство на примере для n=5.
Примем: x=2n=10; y=2n-1=9;cosC=0,337 (см. Формулы 6 и 7).
z0
2
=102
+92
-2*10*9*0,337=120,34.
В ряду квадратов это число находится между числами 100 и 121, являющимися квадратами целых чисел 10 и 11.
Кв. корень из числа 120,34 равен 10.97 – нецелое число.
Проверка: 105
+95
=159049. Корень пятой степени из числа 159049 равен 10,97. В случае необходимости z0
2
может быть уточнено путем повторного (многократного) определения cosC по трем известным сторонам треугольника.
Примечание.
Числа ряда квадратов относятся к остроугольным треугольникам различных степеней n . Числа второго ряда, отмеченные жирным шрифтом и поделенные на 4, указывают на степень n, к которой относится пара чисел, выбранная из условия ограничения a=b=1, в соответсвии с формулой (6).
Четвертый метод
основан на том, что аналогичные степенные ряды могут быть построены для любых n . Тогда для произвольно выбранной степени n=k представляется возможным непосредственно убедиться в том , что извлеченный корень степени k из числаzk
=xk
+yk
является нецелым числом.
P
.
S
. Встает вопрос: при каких условиях нецелое число 10,97... , возведенное в степень n=5 , превратится в целое число 159049 ? Напрашивается ответ: число 10.97... должно быть иррациональным т.е иметь после запятой неограниченное количество значащих цифр.
Остановимся на обосновании принятых в статье допущений (ограничений).
Принятие a
=1
обусловлено получением максимальных 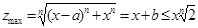 ,
(*) при которых для всех a
<1 нет решений уравнений Ферма в целых числах, а zn
наиболее близок к 2
xn
.
,
(*) при которых для всех a
<1 нет решений уравнений Ферма в целых числах, а zn
наиболее близок к 2
xn
.
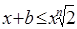 Принятие b
=1
обусловлено тем, что 1 является единственным для всех n целым числом. Это подтверждается следующими соображениями. Из уравнения (*) имеем: , откуда b
£
x
(
n
Ö
2-1)
. Подставляя вместо х его близкое целое значение 2
n
,
получим формулуb
£
2
n
(
n
Ö
2-1)
для практических расчетов, которые свидетельствуют о том, что вблизи начала координат ( на удалении х для каждой степени n) b изменяется от 1,65 при n=2 до 0 при возрастании n до ¥. Отсюда вывод: в растворе 450
сектора всюду b является нецелым числом, исключающим получение целых x,y,z при решении уравнений (1) и (2), за исключением одной точки, где b =1, которую следует проверять на наличие решения в целых числах x,y,z, что и было проделано выше с отрицательным результатом. Принятие b
=1
обусловлено тем, что 1 является единственным для всех n целым числом. Это подтверждается следующими соображениями. Из уравнения (*) имеем: , откуда b
£
x
(
n
Ö
2-1)
. Подставляя вместо х его близкое целое значение 2
n
,
получим формулуb
£
2
n
(
n
Ö
2-1)
для практических расчетов, которые свидетельствуют о том, что вблизи начала координат ( на удалении х для каждой степени n) b изменяется от 1,65 при n=2 до 0 при возрастании n до ¥. Отсюда вывод: в растворе 450
сектора всюду b является нецелым числом, исключающим получение целых x,y,z при решении уравнений (1) и (2), за исключением одной точки, где b =1, которую следует проверять на наличие решения в целых числах x,y,z, что и было проделано выше с отрицательным результатом.
Расчеты при a=b=2,3,4…. относятся к точкам на значительном удалении от начала координат, кратным коэффициентам a=2,3,4….
Результаты расчетов при этом аналогичны выполненным при а=b=1, за исключением случаев, когда х определяется целым числом с конечным числом значащих цифр после запятой. Тогда можно подобрать такой коэффициент пропорциональности а
умножение на который нецелых чисел х,у,z сделает их целыми числами, для которых будет справедливо (
x
*
a
)
n
+(
y
*
a
)
n
=(
z
*
a
)
n
.
В этом случае теорема Ферма станет недостоверной или имеющей исключения при n>2. В принципе теорема Ферма может считаться достоверной, если добавка P
(
a
,
n
)/
xn
-1
является иррациональным числом. Тогда невозможно использовать коэффициент пропорциональности a
.
В иррациональности добавкиP
(1,
n
)/
xn
-1
можно убедиться, если проводить многократное уточнение величины х
методом последовательных приближений, ибо при делении целых числителей в добавке на нецелые, многократно уточняемые знаменатели, в составе добавки найдется хотябы один иррациональный результат деления, который превратит всю добавку в иррациональное число.
Наконец, анализируя расположение секторов на плоскости (x,y) и , учитывая, что нечетные функции xn
и
yn
могут принимать положительные и отрицательные значения, можно составить следующую схему расположения этих функций на плоскости (x,y), т.е. в области распостранения условий теоремы Ферма:
- вся плоскость (x,y) - для четных показателей степени n
- квадрант I - для положительных x и y
- квадрант III- для отрицательных x и y
- в квадрантах II и IVдля нечетных n будут иметь место разности типа xn
-
yn
или yn
-
xn
,
рассмотрение которых теоремой Ферма не предусмотрено.
ВЫВОДЫ
1. Разработан метод доказательства теоремы Ферма в общем виде. Определены основное уравнение (3) и рабочие формулы (2), (5), (6), (7) для проведения анализа и расчетов.
2. Решение уравнений Ферма в нецелых числах при n>2 обусловлено образованием на плоскости (x,y) искаженных (остроугольных) проекций функции yn
+
xn
=
zn
. При проекциях в виде прямоугольных треугольников решения получаются в целых числах.
3. Теорема Ферма распространяется на всю плоскость (x,y), кроме II и IV квадрантов при нечетных n.
Николай Иванович Пичугин, ветеран ВОВ иВС,
Москва 2001 – 2004 год
Т. 396 –90-24
e –meil:hrendy@rumbler.ru
|