2. Теплоты нейтрализации NaOH и NH4
OH соляной кислотой соответственно равны
– 55,9 кДж/моль и – 51,34 кДж/моль. Рассчитать теплоту диссоциации NH4
OH.
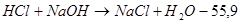 (1) (1)
Сокращенное ионное уравнение: 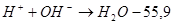 (2) (2)
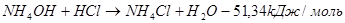 (3) (3)
Ионное уравнение: 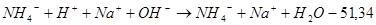 (4) (4)
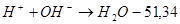 (5) (5)
Отнимаем уравнение 2 от уравнения 4 и получаем:
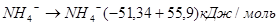 (6) (6)
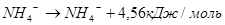 (7) (7)
Ответ: 4,56 кДж.
17. При температуре 298 К реакция заканчивается через 2,5 ч. Рассчитать, при какой температуре она закончится через 20 мин., если температурный коэффициент реакции равен 3.
Решение.
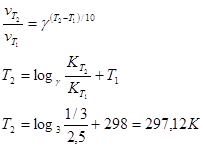 Ответ: 297 К Ответ: 297 К
22. Рассчитать максимальное количество фаз, которые могут сосуществовать в различных системах, состоящих только из молекул Н2
О. Понятие тройной точки на диаграмме состояния воды.
В соответствии с правилом фаз Гиббса для равновесной гетерогенной системы число фаз плюс число степеней свободы равно числу компонентов плюс два:
Ф + С = К + 2.
число фаз Ф= К+2-С
Для воды: Ф=2+2-1=3
Понятие тройной точки на диаграмме состояния воды:
В тройной точке на диаграмме состояния воды находится равновесное состояние всех трех фаз. Если в других точках параметры системы можно изменять, то в точке равновесия фаз этого делать нельзя, так число степеней свободы в этой точке равно нулю.
42. Удельная и эквивалентная электропроводность раствора, их взаимосвязь и зависимость от степени и константы диссоциации электролита.
Электропроводность (способность проводить ток под действием постоянного электрического поля) растворов электролитов обусловлена переносом вещества (направленным движением ионов) и его химическими превращениями. В этом случае раствор называется проводником второго рода. Электропроводность такого раствора зависит прежде всего от природы электролита (от подвижности ионов), его концентрации в растворе, вязкости и температуры самого раствора и др. В проводниках первого рода (к ним относятся преимущественно металлы) переноса вещества не происходит.
Удельная электропроводность – величина, обратная удельному сопротивлению:
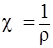
где cудельная электрическая проводимость, Ом – 1.
см – 1
;
ρ – удельное электрическое сопротивление, Ом · см.
Эквивалентная электропроводность – величина электропроводности, отнесенная к одному моль – эквиваленту электролита:
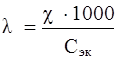 , ,
где λ – эквивалентная электропроводимость, Ом – 1
· см2
· моль– 1
;
Реклама

Сэк
– молярная концентрация эквивалентов раствора электролита, моль/л.
Эквивалентная электропроводность зависит от подвижности анионов и катионов и возрастает с увеличением разбавления, достигая предельного значения в бесконечно разбавленном растворе. В этом случае
= o
–
+ o
+
,
где 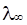 – эквивалентная электропроводность в бесконечно разбавленном растворе, Ом – 1
см2
моль– 1
; о
+
и
о
–
– предельные подвижности ионов (эквивалентные электроподвижности катиона и аниона при бесконечном разбавлении), Ом – 1
· см2
. – эквивалентная электропроводность в бесконечно разбавленном растворе, Ом – 1
см2
моль– 1
; о
+
и
о
–
– предельные подвижности ионов (эквивалентные электроподвижности катиона и аниона при бесконечном разбавлении), Ом – 1
· см2
.
Уравнение представляет собой эмпирический закон Кольрауша: эквивалентная электропроводность при бесконечном разбавлении равна сумме предельных электроподвижностей ионов.
Эквивалентная электропроводность зависит также от степени диссоциации и константы диссоциации электролита, которые связаны уравнениями:
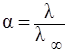
где α – степень диссоциации электролита,
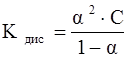 , ,
где Кдис
– константа диссоциации электролита;
С – молярная концентрация раствора, моль/л.
57. Процессы самопроизвольного диспергирования и пептизации. Привести конкретные примеры этих явлений для продуктов питания и дать им обоснование.
В отличие от лиофобных существуют дисперсные системы, возникающие в результате самопроизвольного диспергирования макроскопических фаз. Такие дисперсные системы термодинамически равновесны и не нуждаются к дополнительной стабилизации. Их называют лиофильными. К таким cистемам относятся критические эмульсии, возникающие в узком температур ном интервале вблизи критической температуры смешения двух жидкий фаз, растворы коллоидных (мицеллярных) ПАВ, а также некоторые высокомолекулярные соединения (ВМС), в молекулах которых имеются резко различающиеся по полярности участки.
Наиболее характерными представителями лиофильных коллоидных систем являются растворы мицеллообразующих ПАВ. В таких системах и одном и том же растворителе в равновесии могут находиться ионы (или молекулы) и коллоидные частицы. Образование коллоидных частиц мицелл в таких системах связано с диссоциацией дифильных молекул растворенного вещества (со степенью диссоциации т ~ 20—100).
При малых концентрациях ПАВ образуют истинные растворы, то есть частицы диспергированы в них до отдельных молекул (или ионов). По мере увеличения концентрации возникают мицеллы. В водных растворах органические части молекул в мицеллах объединяются в жидкое углеводородное ядро, а полярные гидратированные группы находятся в воде, при этом общая площадь контакта гидрофобных частей молекул с водой резко сокращается. Благодаря гидрофильности полярных групп, окружающих мицеллу, поверхностное (межфазное) натяжение на границе ядро — вода понижено до значений, обеспечивающих термодинамическую устойчивость таких агрегатов по сравнению с молекулярным раствором и макрофазой ПАВ.
Реклама

Способностью к мицеллообразованию обладают не все ПАВ, а только те, которые имеют определенный гидрофильно-липофильный баланс и строение, в частности, достаточно сильные полярные группы, способные экранировать аполярное ядро на достаточно большой площади, и длинные, но гибкие гидрофильные цепи. Молекулы со слабыми полярными группами (ОН, NH2
, СООН) или с короткими углеводородными цепями (менее С7
), или с жесткими ароматическими, или алициклическими, аполярными, частями (например, многие красители) мицелл не образуют, хотя и могут объединяться в димеры и тримеры.
Некоторые ПАВ, имеющие два длинных углеводородных радикала (лецитин, кефалин), могут образовать в растворе дисссоциаты другого типа, называемые везикулами. Эти структуры представляют собой замкнутые многослойные или бислойные пленки с заключенной между ними водной фазой.
Критическая концентрация мицеллообразования (ККМ) определяется как концентрация (или очень узкая область концентраций), при которой возникает большое число мицелл и резко изменяется ряд свойств раствора. ККМ соответствует качественному изменению системы — превращению гомогенного раствора в микрогетерогенную коллоидную систему. Этот переход проявляется в резком изменении различных экспериментально обнаруживаемых свойств на зависимостях от концентрации ПАВ — поверхностного натяжения, светорассеяния, электрической проводимости и т. д.
При малых замицеллярных концентрациях образуются сферические мицеллы (мицеллы Гартли) с жидким аполярным ядром.
Мицеллы из ионогенных ПАВ заряжены, внутренняя обкладка ДЭС образована ионогенными группами ПАВ, а внешняя — свободными или частично связанными противоионами. Доля связанных ионов р обычно равна 0,2—0,6, например для калиевых солей фторуглеродных кислот р = 0,52.
При более высоких концентрациях наряду с увеличением количества (числа) сферических мицелл происходит изменение их формы с превращением их в анизодиаметричные, более упорядоченные агрегаты (мицеллы Мак-Бена — эллипсоидальные, цилиндрические, пластинчатые и другие псевдофазы, называемые мезофазами. Структура ленточных и пластинчатых мицелл подобна многослойным (стратифицирующим) пенным и эмульсионным пленкам, возникающим при утончении толстых пленок из концентрированных растворов многих ПАВ.
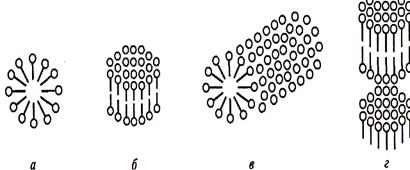
Рис.1. Формы мицелл: а — сферические; 6 — дискообразные; в — цилиндрические; г — пластинчатые
Числа агрегации мицелл обычно равны 20—100, т. е. недостаточно не лики, чтобы можно было считать мицеллу макроскопической фазой. Совокупность мицелл, однако, можно считать «псевдофазой».
Энергетика образования мицелл диктует условия выгодности существования мицелл с некоторой оптимальной степенью диссоциации и оптимальным радиусом, соответствующим приблизительно вытянутой длине углеводородной цепи (несколько меньше). Например, минимальный диаметр мицелл додецилсульфата натрия равен 5,5 нм, а степень диссоциации — 65 (при Т=25°С).
В неводных средах могут возникать обратные мицеллы с ориентации ПАВ, противоположной той, которая существует в водных мицеллах. И кратных мицеллах полярные группы объединяются в гидрофильное ядро, гидрофобные цепи обращены в аполярную среду. Склонность к самодиссоциации в аполярных средах выражена гораздо слабее. Степень диссоциации в обратных мицеллах оказывается значительно меньше (обычно т < 15 , чем в прямых мицеллах, что связано с геометрией молекул, влияющей на энергетическую выгодное именно таких малых мицелл.
62. Определить осмотическое давление гидрозоля золота с массовой концентрацией дисперсной фазы 2 кг/м3
при температуре 293 К, учитывая что диаметр частиц 6·10-9
м, а плотность дисперсной фазы 19,3·103
кг/м3
.
Величина осмотического давления определяется только частичной концентрацией (концентрацией дисперсных частиц) и не зависит от их природы и размера. Для разбавленных дисперсных систем осмотическое давление рассчитывается по уравнению, аналогичному уравнению Вант-Гоффа:
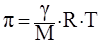 , ,
где 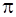 – осмотическое давление, Н/м2
; – осмотическое давление, Н/м2
;
γ – массовая концентрация раствора, кг/м3
;
М – мицеллярная масса вещества, кг/кмоль.
Для растворов высокомолекулярных соединений частичная масса совпадает с молярной.
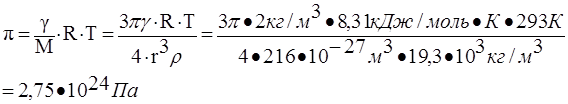 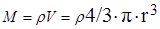
Ответ: 22,3*1023
Па.
77. Адсорбционная хроматография. Уравнения изотермы адсорбции, их анализ и области применения.
Адсорбция – процесс самопроизвольного поглощения вещества (адсорбтива) поверхностью адсорбента. Уравнение Гиббса устанавливает взаимосвязь величины адсорбции (Г, кмоль/кг или кмоль/м 2
) с изменением поверхностного натяжения (Дж/м2
от концентрации раствора (С, кмоль/л). 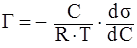 , ,
где С – концентрация раствора, кмоль/л;
R– универсальная газовая постоянная;
T – температура;
d/dС – производная, являющаяся мерой поверхностной активности; может быть определена графически по зависимости поверхностного натяжения от концентрации (при 0).
Физические процессы молекулярной адсорбции на твердой поверхности описываются уравнениями Ленгмюра и Фрейндлиха.
Уравнение Ленгмюра:
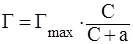 , ,
где Г – величина адсорбции, кмоль/кг или кмоль/м2
;
Гmax
– величина предельной адсорбции, кмоль/кг (кмоль/м2
);
С – концентрация раствора, кмоль/л;
а – константа равновесия адсорбции.
Это уравнение хорошо описывает адсорбцию для малых и больших концентраций растворов (или давлений газа).
Эмпирическое уравнение Фрейндлиха:
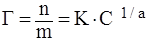 , ,
где Г – величина адсорбции, кмоль/кг (кмоль/м2
);
n – количество вещества-адсорбтива, кмоль;
m – масса адсорбента, кг;
К – константа (при С = 1 моль/л К = Г);
1/а – константа (адсорбционный показатель); зависит от природы адсорбента и температуры. 1/а = 0,1–1.
Уравнение (2.11) хорошо описывает адсорбцию для интервала средних концентраций растворов (или давлений газа).
Адсорбция на жидкой поверхности может приводить как к уменьшению поверхностного натяжения (например, при адсорбции малорастворимых, дифильных поверхностно-активных веществ), так и к его увеличению (в частности, при адсорбции поверхностно-инактивных веществ, т. е. хорошо растворимых в воде неорганических электролитов) или не изменять его (растворы сахаров в воде). В последнем случае вещество распределяется равномерно между поверхностным слоем и объемом раствора.
Адсорбция кислорода на поверхности мелких порошков и аэрозолей в ряде случаев может приводить к резкому ускорению процесса окисления дисперсной фазы, что может стать причиной самовозгорания и даже взрыва, например, мелкодисперсной муки, мучной, сахарной пыли и т. п. Ионная адсорбция может быть обратимой или необратимой. Обратимая адсорбция является основой ионообменной хроматографии.
Газовая хроматография может быть разделена на газо-адсорбционную (газо-твердую) и газо-жидкостную. В первом случае неподвижной фазой служит твердое вещество — адсорбент, во втором — жидкость, распределенная тонким слоем по поверхности какого-либо твердого носителя (зерненого материала, стенок колонки).
82. В каком объемном соотношении следует смешать 0,029 %-ный раствор
NaCl
и 0,001 н раствор
AgNO
3
, чтобы получить незаряженные частицы золя
AgCl
? Плотность раствора
NaCl
равна 1 г/мл.
Решение. Запишем уравнение реакции:
NaCl + AgNO3
= AgCl + NaNO3
0,029 0,001 н.
Запишемформулумицеллы: [m (AgСl) n Cl–
· (n-1) Ag+
]1–
x Ag+
Для того, чтобы ее получить, следует взять в избытке раствор NaCl.
Исходя из формулы %-ной концентрации вещества можно записать, что:
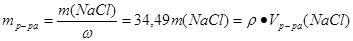
Для того, чтобы определить массу растворенного нитрата серебра, воспользуемся формулой:
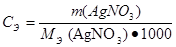
Откуда масса вещества AgNO3
равна:
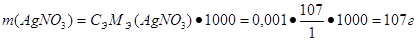
По уравнению масса хлорида натрия:
х_-------------------------107 г.
58 г/моль------------------107г/моль
х=58 г
Объем раствора хлорида натрия:
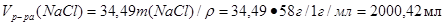
Объем раствора нитрата серебра
2000, 42 мл----------------------------х мл
58 г/моль 107 г/моль
х = 2000, 42*107 /58 = 3690,43 мл
Соотношение объемов веществ: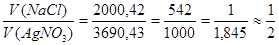
98. Коагуляция дисперсной системы. Скорость коагуляции. Причины, вызывающие процесс самопроизвольной коагуляции.
Коагуляция – процесс самопроизвольного укрупнения (слипания) дисперсных частиц, который может происходить при действии на дисперсную систему различных факторов: при интенсивном перемешивании или встряхивании, нагреве или охлаждении, облучении светом или пропускании электрического тока, при добавлении к системе электролитов или неэлектролитов и др. При разных способах воздействия на систему происходит уменьшение энергии связи диспергированных частиц с окружающей их дисперсионной средой. Так, добавление электролита вызывает сжатие диффузного слоя в коллоидной частице, следовательно, понижение величины электрокинетического потенциала. Это приводит к уменьшению электростатического отталкивания коллоидных частиц и, как следствие, к большей вероятности их слипания.
Минимальная концентрация электролита, добавляемого к дисперсной системе, при которой наступает явная коагуляция за определенный промежуток времени, носит название порога коагуляции 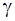 . Порог коагуляции определяется температурой, природой добавленного электролита, знаком заряда добавляемого иона (действует прежде всего ион, имеющий заряд, противоположный заряду коллоидных частиц) и величиной заряда этого иона. Так, для трех-, двух- и однозарядных ионов явная коагуляция наступает при концентрации электролитов в соотношении 1:10 - 50: 500-1000 (приближенное правило Шульце-Гарди). . Порог коагуляции определяется температурой, природой добавленного электролита, знаком заряда добавляемого иона (действует прежде всего ион, имеющий заряд, противоположный заряду коллоидных частиц) и величиной заряда этого иона. Так, для трех-, двух- и однозарядных ионов явная коагуляция наступает при концентрации электролитов в соотношении 1:10 - 50: 500-1000 (приближенное правило Шульце-Гарди).
Порог коагуляции рассчитывается следующим образом:
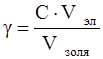 , (1) , (1)
где порог коагуляции, кмоль/м3
;
С – молярная концентрация раствора электролита, кмоль/м3
;
Vэл
– объем раствора электролита, м3
;
Vзоля
– объем золя, м3
.
Теорию быстрой скорости коагуляции разработал Смолуховский. Он автор уравнения для расчета константы скорости коагуляции K:
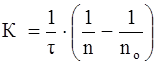 , (2) , (2)
где n0
и n – число частиц в единице объема системы до начала коагуляции и к моменту времени 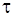 соответственно соответственно
время коагуляции, с.
Константа скорости коагуляции зависит от коэффициента диффузии для частиц и их радиуса следующим образом:
К = 8 · ·D · r. (3)
Учитывая уравнение (2) и уравнение Эйнштейна, окончательное уравнение для константы скорости коагуляции принимает вид:
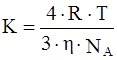 , (4) , (4)
где К – константа скорости коагуляции, м3
/с;
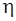 – вязкость среды, Па·с; – вязкость среды, Па·с;
NA
– число Авогадро.
Смолуховский ввел также понятие о времени половинной коагуляции, согласно которому время, необходимое для уменьшения первоначального числа частиц в 2 раза, связано с их исходным числом следующим образом:
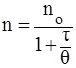 , (5) , (5)
где – время половинной коагуляции, с;
– время от начала коагуляции, с.
Из уравнения, преобразованного к виду:
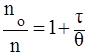 , (6) , (6)
следует, что если построенный в координатах nо
/n = f ( график представляет собой прямую линию, то это служит показателем соответствия экспериментальных данных теории Смолуховского.
107. Эмульсии. Условия их образования, классификация и свойства. Примеры эмульсий среди продуктов питания.
Эмульсиями называются дисперсные системы, в которых дисперсионная среда и дисперсная фаза находятся в жидком состоянии. Эмульсии являются обычно грубодисперсными системами. Такие системы часто встречаются в природе, например, молоко, млечный сок каучуконосных растений. В первом случае жир, а во втором - углеводород каучука диспергированы в воде. Оба эти вещества почти совершенно не растворяются в дисперсионной среде т.е. в воде. Таким образом, эмульсии - это микрогетерогенные системы, состоящие из двух практически взаимно-нерастворимых жидкостей, которые очень сильно отличаются от друг-друга по характеру молекул. Если одна из жидкостей является полярной, например вода, то вторая - должна быть неполярной или малополярной, например, органическая жидкость.
Малополярные органические жидкости - бензол, бензин, керосин, анилин, масло и др.,- независимо от их химической природы, называют маслом.
На практике чаще всего встречаются водные эмульсии, т.е. эмульсии в которых одной из двух жидкостей является вода. Такие эмульсии подразделяются на два типа: масло в воде (сокращенно - м/в) и вода в масле (м/в). В эмульсиях первого типа (прямых) масло является дисперсионной фазой, а вода - дисперсионной средой. В эмульсиях второго типа (обратных) вода является раздробленной в виде капелек дисперсной фазой, а масло - дисперсионной средой.
Для получения эмульсии две несмешивающиеся жидкости подвергают процессу эмульгирования, состоящему в том, что механическим встряхиванием, разбиванием особыми лопастными мешалками или продавливанием через узкие щели жидкости раздробляются друг в друге. В технике имеется большое число механизмов, где диспергирование осуществляется или благодаря простому разбиванию сравнительно больших капель на более мелкие, или растяжением жидкости в пленку, которая, разрываясь, дает массу мелких капелек. Для получения особо высокодисперсных эмульсий применяется ультразвуковой метод.
Эмульсии, полученные из чистых жидкостей, обычно очень неустойчивые, капельки при соприкосновении друг с другим сливаются и дисперсная система постепенно расслаивается на две несмешивающиеся жидкости. Неустойчивость эмульсий объясняется наличием избыточного запаса свободной поверхности на границе фаз, что выражается большим поверхностным натяжением. Процесс расслоения эмульсии идет самопроизвольно, так как при этом система большей степени дисперсности, с большей свободной поверхностной энергией переходит в малодисперсную систему, уменьшая поверхностное натяжение. Процесс самопроизвольного слияния жидких капель, который заканчивается расслоением эмульсии на составляющие её жидкости, называется коалесценцией.
Подобно коллоидным системам, получение устойчивых эмульсий возможно только в присутствии веществ, которые, адсорбируясь на поверхности капелек, препятствуют их слиянию и придают системе агрегатную устойчивость. Вещества, которые обуславливают устойчивость (стабильность) эмульсии называются эмульгаторами.
По своим свойствам, в первую очередь по агрегатной устойчивости, эмульсии делятся на две группы: эмульсии разбавленные, в которых концентрация дисперсионной фазы мала (меньше 1%), и эмульсии концентрированные, в которых концентрация дисперсной фазы значительна (объемная концентрация превышает 1%).
Разбавленные эмульсии характеризуются своей устойчивостью в отсутствии специального эмульгатора (стабилизатора). Обычно концентрация таких эмульсий не превышает 0,1 - 0,01%, благодаря чему вероятность столкновения образующих их капелек дисперсной фазы очень невелика. Такие системы ведут себя вполне аналогично лиофобным золям. Их относительная устойчивость определяется существованием на поверхности капелек эмульсии двойного электрического слоя. Необходимое для этого минимальное количество электролита всегда находится в употребляемом масле в виде примесей.
В концентрированных эмульсиях в отличие от разбавленных при сколько-нибудь значительной концентрации дисперсной фазы, слияние капелек происходит с большей скоростью и эмульсия за короткий промежуток времени разделяется на два слоя. Получение устойчивых концентрированных эмульсий возможно только в присутствии специальных эмульгаторов.
Эмульгаторы, в зависимости от их химической природы, могут стабилизировать эмульсию как путем понижения межфазного поверхностного натяжения, придания частицам эмульсии электрических зарядов, одинаковых по знаку, так и путем образования из эмульгатора на поверхности капелек механически прочных магнитных пленок. Такие пленки защищают частицы эмульсии от взаимного слияния при их столкновении, причем этот фактор может быть более важным, чем действие электрических зарядов. Особенно это относится к концентрированным эмульсиям, в которых эмульгаторы, сообщающие только заряд частицам, уже не обеспечивают устойчивости.
К эмульгаторам, способным образовывать прочные защитные пленки, относятся высокомолекулярные соединения, например, сапонин, белки (желатин, казеин), каучук, смолы, соли жирных кислот (мыла) и др. Указанные вещества, особенно мыла, обладая некоторой поверхностной активностью, адсорбируются на поверхности капель эмульсии и образуют структурированную оболочку, которая является вязкой, прочной и упругой. При соударении частиц такая оболочка обычно не разрушается и не выдавливается, благодаря чему эмульсии и приобретают высокую устойчивость.
Наибольший интерес представляют собой желатированные или твердые эмульсии. В них, как и в подобных суспензиях, стабилизирующее действие эмульгатора переходит в структуризующее.
Желатированные эмульсии характеризуются большой устойчивостью, прочностью и другими механическими свойствами, которые обусловлены наличием в них тончайшей структуры. Эта структура - сетка-каркас из двухмерного студня, построенного из высокополимерного эмульгатора. Примерами таких эмульсий являются консистентные смазки, маргарин, сливочное масло, густые кремы. Обычными эмульсиями являются молоко, сливки, жидкости, применяемые при обработке металлов.
Эмульсии со временем разрушаются. В некоторых случаях возникает необходимость ускорить разрушение эмульсий, например, разрушение эмульсии в сырой нефти. Ускорить процесс разрушения можно всеми путями, ведущими к уменьшению прочности защитной пленки эмульгатора и увеличению возможности соприкосновения частиц друг с другом.
Методов разрушения эмульсии (деэмульгирования) очень много. Наиболее важными из них являются следующие:
1. Химическое разрушение защитных пленок эмульгатора, например, действием сильной минеральной кислоты.
2. Прибавление эмульгатора, способного вызвать обращение фаз эмульсии и снижающего этим прочность защитной пленки.
3. Термическое разрушение - расслоение эмульсий нагреванием. С повышением температуры уменьшается адсорбция эмульгатора, что ведет к разрушению эмульсии.
4. Механическое воздействие. К этому методу относится механическое разрушение стабилизированных пленок, например, сбивание сливок в масло. Центрифугирование также относится к механическому воздействию.
5. Действие электролитов вызывает разрушение эмульсий, стабилизированных электрическим зарядом частиц.
Эмульсии находят применение во многих химико-технологических процессах - в мыловарении, в производстве молочных продуктов, в производстве эмульсионных красок, в производстве каучуков путем полимеризации, в производстве пластмасс и в других производствах.
ЛИТЕРАТУРА
1. Ахметов Б. В. Задачи и упражнения по физической и коллоидной химии. – Л.: Химия, 1989.
2. Гамеева О. С. Физическая и коллоидная химия. – М.: Высшая школа, 1983.
3. Евстратова К. И., Купина Н. А., Малахова Е. М. Физическая и коллоидная химия. – М.: Высшая школа, 1990.
4. Зимон А. Д., Лещенко Н. Ф. Коллоидная химия. – М.: Химия, 2001.
5. Зимон А. Д., Лещенко Н. Ф. Физическая химия. – М.: Химия, 2000.
6. Киселев Е. В. Сборник примеров и задач по физической химии. – М.: Высшая школа, 1983.
7. Кнорре Д. Г. Физическая химия. – М.: Высшая школа, 1990.
8. Стромберг А. Г. Физическая химия. – М.: Высшая школа, 2001.
9. Степин Б. Д. Международные системы единиц физических величин в химии. – М.: Высшая школа, 1990.
10. Фридрихсберг Д. А. Курс коллоидной химии. – Л.: Химия, 1995.
11. Хмельницкий Р. А. Физическая и коллоидная химиия. – М.: Высшая школа, 1988.
|