СОДЕРЖАНИЕ
Введение
1. Временные ряды и методы их расчета
1.1. Случайные события и величины
1.2. Числовые характеристики распределения случайной величины
1.3. Теоретические сведения о временных рядах
1.3.1. Метод экспоненциального сглаживания
1.3.2. Метод скользящего среднего
1.3.3. Метод Брауна
1.3.4. Метод среднего темпа
2. Статистический показатель расчетов временных рядов (корреляция)
Заключение
Список использованной литературы
Приложение 1. Исходные данные
Приложение 2. Метод экспоненциального сглаживания
Приложение 3. Метод скользящего среднего
Приложение 4. Метод Брауна
Приложение 5. Метод среднего темпа
введение
Моделирование — это процесс создания модели, а под моделью понимают искусственно созданный образ предмета, устройства, процесса.
Вид деятельности, направленный на получение, обработку и анализ информации называется статистикой. Статистика — наука, изучающая не отдельные факты, а явления и процессы в целом.
Объектом статистического исследования в статистике является статистическая совокупность. Статистическая совокупность — это множество единиц, обладающих массовостью, однородностью, целостностью и наличием вариантов. Каждый отдельный элемент этого множества называется единицей статистической совокупности.
Статистической закономерностью называют одну из форм причинной связи, которая характеризуется последовательностью, регулярностью повторения событий с определенной степенью вероятности.
Любая статистическая закономерность устанавливается на основе анализа массивов данных. Статистика печати изучает количественные и качественные изменения в издательском деле в целом, что позволяет определить особенности развития печати.
1. Временные ряды и методы их расчета
1.1. Случайные события и величины
Событием называется любой факт, который в результате деятельности может произойти или не произойти. Всякое отдельное множество отличающихся друг от друга по величине событий, но имеющих одну систему измерения составляет совокупность.
Число единиц совокупности характеризуется определенными признаками. Каждый признак у разных единиц совокупности может принимать различные значения. Это различие между единицами совокупности называется вариацией (дисперсией).
Реклама

Если величина изменяет свое значение под влиянием различных случайных величин, то она называется случайной переменной. Наиболее общая совокупность, содержащая множество случайных величин, называется генеральной совокупностью. Выборка из генеральной совокупности называется выборочной совокупностью. Задачей изучения совокупности является нахождение статистических характеристик, которые позволяют судить о поведении системы.
Определенный набор случайных величин, имеющих некоторые ограничения, называют случайным событием. Для случайных величин значения параметров заранее предсказать невозможно. Многократное повторение измерений случайного события дает возможность получить определенные закономерности, т. е. определить частоту возникновения одного события.
Вероятность любого события определяется как соотношение благоприятных исходов (а
) к общему числу исходов (n
), т. е.
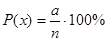 |
(1.1) |
Вероятность любого события изменяется от 0 до 1, если в долях, и от 0 до 100, если в процентах.
Если 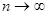 , то вероятность события приближается к 0 ( , то вероятность события приближается к 0 (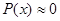 ). ).
Если 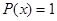 , то событие называют достоверным. , то событие называют достоверным.
Если 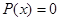 , то событие называют невозможным. , то событие называют невозможным.
Два события называют независимыми, если появление одного из них не зависит от появления другого.
Случайные величины могут быть дискретными и непрерывными. Для дискретных случайных величин различия между вариантами случайных величин выражаются целыми числами. Совокупность возможных значений случайной величины и вероятность того, что она примет определенное значение образуют закон распределения случайной величины.
Распределение дискретных случайных величин показывается в виде таблицы, в которой каждому значению случайной величины соответствует ее вероятность. Для непрерывной случайной величины составление ряда распределения заключается в том, что диапазон всех значений случайной величины разбивается на некоторое количество интервалов. Для каждого интервала измеряется количество попаданий в этот интервал. На основании этого рассчитывается вероятность попадания по каждому интервалу. Результат выводится в виде гистограммы.
Наиболее общую характеристику распределения дискретной или непрерывной величины дает интегральный закон распределения. Он устанавливает вероятность того, что случайная величина (х
) остается меньше некоторой количественной переменной (А
), т. е.
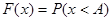 , , |
(1.2) |
где 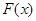 — интегральная функция распределения. — интегральная функция распределения.
При изменении случайной величины (х
) от минимального значения до максимального, интегральная функция распределения 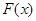 изменяется в диапазоне от 0 до 1. изменяется в диапазоне от 0 до 1.
Реклама

1.2. Числовые характеристики распределения случайной величины
Количество попаданий случайной величины в определенный интервал характеризуется плотностью распределения случайной величины. Одной из основных характеристик является математическое ожидание.
Для дискретной случайной величины математическое ожидание определяется как сумма произведений всех возможных значений случайной величины на вероятность этих значений.
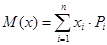 |
(1.3) |
Для непрерывной случайной величины математическое ожидание равно:
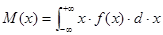 |
(1.4) |
Таким образом, математическое ожидание выступает как средневзвешенное значение случайной величины и характеризует положение центра распределения на оси абсцисс.
На практике математическое ожидание для непрерывной случайной величины рассчитывается по формуле:
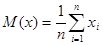 |
(1.5) |
Для дискретной случайной величины по формуле:
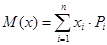 |
(1.6) |
Кроме математического ожидания для характеристики положения центра распределения случайной величины часто используют моду и медиану.
Мода — это значение случайной величины, которому соответствует наибольшая плотность вероятности ее распределения.
Медиана — это значение случайной величины для которого интегральная функция распределения 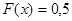 . .
Для расчета значения моды и медианы необходимо сначала определить модальный и медиальный интервалы.
Модальный интервал — это интервал, характеризующийся наибольшим количеством попаданий случайной величины.
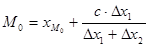 , , |
(1.7) |
где 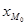 — нижняя граница модального интервала; — нижняя граница модального интервала;
с
— величина интервала;
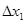 — разность числа попаданий случайной величины в модальном интервале и предыдущем; — разность числа попаданий случайной величины в модальном интервале и предыдущем;
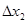 — разность числа попаданий случайной величины в модальном интервале и последующем. — разность числа попаданий случайной величины в модальном интервале и последующем.
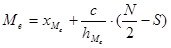 , , |
(1.8) |
где 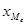 — нижняя граница медиального интервала; — нижняя граница медиального интервала;
с
— величина интервала;
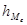 — количество попаданий случайной величины в медиальный интервал; — количество попаданий случайной величины в медиальный интервал;
N
— общее число опытов;
S
— сумма исходов, соответствующая попаданию случайной величины по интервалам, не превышающим количество 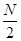 . .
Для описания рассеивания случайной величины вокруг математического ожидания используют дисперсию. На практике для расчета дисперсии используют следующую формулу:
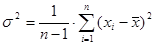 , , |
(1.9) |
где n
— объем выборки (количество измерений);
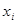 — значение случайной величины; — значение случайной величины;
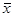 — среднее значение случайной величины. — среднее значение случайной величины.
Среднеквадратичное стандартное отклонение рассчитывается по формуле:
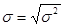 |
(1.10) |
Для сравнения величин рассеивания различных случайных величин используют относительное отклонение. Оно рассчитывается по формуле:
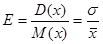 |
(1.11) |
1.3. Теоретические сведения о временных рядах
Временный ряд — это множество наблюдений X
(t
), полученных последовательно за время t
. Анализ временных рядов основан на предположении, что последовательные значения в базе данных фиксируются через определенные промежутки времени. Цели анализа временных рядов (определение природы ряда и прогнозирование) требуют математического описания модели.
Различают детерминированные и случайные временные ряды. Детерминированный ряд — это ряд, значение компонентов которого определяется какой-либо математической зависимостью. Значение компонентов случайного ряда могут быть описаны только с помощью распределения вероятности.
Явления, развивающиеся во времени согласно закону теории вероятности, называются стохастическим процессом. Выделяют два вида стохастических процессов:
1) стационарный. Это процессы, свойства которых не изменяются во времени. Они имеют постоянное математическое ожидание (постоянное среднее значение вокруг, которого варьируются), среднеквадратичное отклонение (определяет разброс компонентов ряда относительно их математического ожидания) и автокорреляцию.
2) динамические. При графическом построении временного ряда результаты наблюдений наносят на график в виде точек и соединяют последовательно ломаной линией. В результате получают линию фактических изменений.
Для определения общих тенденций роста (снижения) показателей временного ряда используют выравнивание (сглаживание), общей картины происходящих процессов и стараются описать их с помощью математических зависимостей.
Сглаживание ряда осуществляется следующими основными способами:
1) методом экспоненциального сглаживания;
2) методом скользящего среднего;
3) методом Брауна;
4) методом среднего темпа;
5) методом регрессионных уравнений.
1.3.1. Метод экспоненциального сглаживания
Метод экспоненциального сглаживания является одним из простейших и распространенных способов выравнивания ряда. Выравнивание осуществляется по следующей формуле:
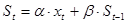 , , |
(1.12) |
где  — значение экспоненциальной средней в момент времени t
; — значение экспоненциальной средней в момент времени t
;
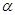 — параметр сглаживания, принимает значения от 0 до 1; — параметр сглаживания, принимает значения от 0 до 1;
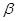 — параметр сглаживания. — параметр сглаживания.
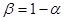 |
(1.13) |
Для расчета первого значения  задается значение задается значение 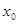 , которое высчитывается по формуле: , которое высчитывается по формуле:
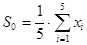 |
(1.14) |
Если в формулу (1.12) подставить формулу (1.13), то получится следующее выражение:
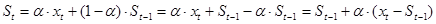 |
(1.15) |
Экспоненциальное среднее  имеет математическое ожидание равное математическому ожиданию имеет математическое ожидание равное математическому ожиданию 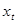 , при этом среднеквадратичное отклонение , при этом среднеквадратичное отклонение  меньше среднеквадратичного отклонения меньше среднеквадратичного отклонения 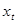 . .
Чем меньше параметр сглаживания, тем в большей степени сокращается среднеквадратичное отклонение  , т. е. экспоненциальное сглаживание служит как фильтр, формирующий на выходе значение , т. е. экспоненциальное сглаживание служит как фильтр, формирующий на выходе значение  и предпосылки для прогноза. и предпосылки для прогноза.
Прогноз рассчитывается по формуле:
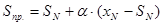 |
(1.16) |
1.3.2. Метод скользящего среднего
Метод скользящего среднего основан на выравнивании ряда с использованием следующей формулы:
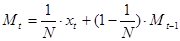 , , |
(1.17) |
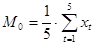 , , |
(1.18) |
где 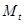 — значение скользящего среднего в момент времени t
; — значение скользящего среднего в момент времени t
;
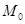 — некоторая величина, характеризующая начальное условие при — некоторая величина, характеризующая начальное условие при 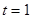 ; ;
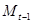 — значение скользящего среднего в момент времени — значение скользящего среднего в момент времени  ; ;
N
— число значений ряда.
1.3.3. Метод Брауна
Метод Брауна основан на использовании адаптивных моделей разного порядка. Адаптивные модели первого порядка основаны на использовании экспоненциальной средней, отличие состоит в выборе 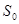 . Начальные условия для расчета: . Начальные условия для расчета:
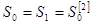 |
(1.19) |
где 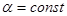
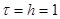 , где , где
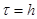 — это шаг. — это шаг.
Расчет производится по следующим формулам:
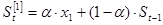 |
(1.20) |
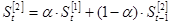 |
(1.21) |
Прогноз следующего значения ряда вычисляется по следующей формуле:
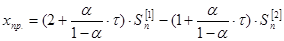 |
(1.22) |
Для построения графических зависимостей пользуются столбцами значений: х
и 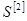 . .
1.3.4. Метод среднего темпа
При использовании этого метода в расчете учитывается вся информация ряда. Расчет базируется на предпосылке о том, что сумма фактических уровней динамического ряда или суммарный рост за период должен быть равен сумме уровней, полученных расчетным путем исходя из начального уровня ряда и среднего темпа роста (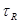 ). ).
Он производится по формуле:
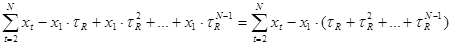 |
(1.23) |
Расчет уровня ряда:
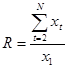 , , |
(1.24) |
где 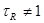 . .
Расчет проводится путем подбора 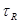 при соблюдении следующего условия: при соблюдении следующего условия:
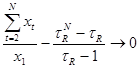 |
(1.25) |
Когда определено значение 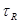 , при котором , при котором 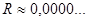 , найденное значение среднего темпа роста выступает в качестве коэффициента для составления прогноза на будущий срок. , найденное значение среднего темпа роста выступает в качестве коэффициента для составления прогноза на будущий срок.
Высчитывается по формуле:
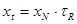 |
(1.26) |
2. Статистический показатель расчетов
временных рядов (корреляция)
Случайной величиной
называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Случайная величина называется дискретной, если ее возможные значения можно пронумеровать. Основными формами задания дискретной случайной величины являются: 1) ряд распределения; 2) функция распределения (интегральная функция распределения).
Математическое ожидание дискретной случайной величины
Х
называется значение, рассчитанное по формуле
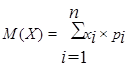 . (2.1) . (2.1)
Математическое ожидание обозначается также mx
.
Оно приближенно равно среднему возможному значению случайной величины.
Случайная величина называется непрерывной
, если ее возможные значения сплошь заполняют некоторый интервал. Основными формами задания непрерывной случайной величины являются:
· интегральная функция распределения F(x);
· функция плотности вероятности f(x).
Интегральная функция распределения
для непрерывной случайной величины Х
определяется так же, как и для дискретной F
(x
) = P
(X
<
x
).
Плотность вероятности
(дифференциальной функцией распределения
) случайной величины Х
называется функция
f
(
x
) =
F
´
(x
). (2.2)
Для непрерывной случайной величины Х
функция распределения F
(x
) непрерывна на всей оси Ох
, а плотность вероятности f
(x
) существует везде, за исключением, может быть, конечного числа точек.
Математическим ожиданием
mx
непрерывной случайной величины Х
, для которого функция f
(x
) является плотностью вероятности, называется величина несобственного интеграла
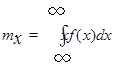 , (2.3) , (2.3)
еслион сходится.
Дисперсией
называется значение несобственного интеграла
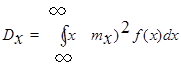 , (2.4) , (2.4)
если он сходится.
При вычислении дисперсии иногда удобна формула
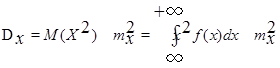 . (2.5) . (2.5)
Кроме математического ожидания для характеристики положения центра распределения случайной величины часто используют моду и медиану. Модой
называется то значение случайной величины, которому соответствует наибольшая плотность вероятности ее распределения.
Медианой
называется значение случайной величины, для которой интегральная функция распределения F
(x
) = 0,5.
Для того чтобы рассчитать значения моды и медианы, необходимо вначале определить модальный и медиальный интервал. Модальный интервал на гистограмме отвечает наибольшей частоте попадания случайной величины. Моду рассчитывают по формуле
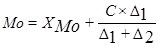 , (2.6) , (2.6)
где ХМо
– нижняя граница модального интеграла; С
– величина интервала (разность между верхней и нижней границами); Δ1
– разность числа попаданий случайной величины в модальный интервал и предыдущий интервал; Δ2
– разность попаданий случайной величины в модальный интервал и последующий интервал.
Медиальный интервал определяется по формуле
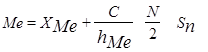 , (2.7) , (2.7)
где ХМе
– нижняя граница медиального интервала С
; h
Ме
– количество попаданий случайной величины в медиальный интервал; N
– общее количество опытов; Sn
– сумма исходов, соответствующих попаданию случайной величины в интервалы, не превышающие количество N
/2.
Корреляция
Существуют две категории связей или зависимостей между признаками: функциональные и корреляционные. При функциональной зависимости каждому значению одной переменной соответствует одно значение другой переменной.
Связь случайной величины всегда носит вероятностный характер. Следовательно одному значению одной случайной величины соответствует несколько значений другой случайной величины. Такая зависимость называется корреляционной.
Самым простым случаем вероятностной связи является корреляция двух факторов — парная корреляция. Наглядное представление о парной корреляции дает корреляционное поле — графическое изображение точек, координаты которых соответствуют значениям случайных величин.
Различают положительную и отрицательную корреляции. При положительной корреляции зависимость между случайными величинами прямая, т. е. при увеличении значений одной случайной величины увеличиваются и значения второй случайной величины. При отрицательной корреляции увеличению значений одной случайной величины соответствует уменьшение значений второй случайной величины.
Связь двух факторов тем больше, чем теснее располагаются точки около некоторой линии, отображающей график зависимости одной случайной величины от другой. Если все точки корреляционного поля попадают на эту линию, то теснота связи окажется максимальной, и получается функциональная зависимость двух случайных величин. Для количественного определения тесноты связи между двумя случайными величинами в случае линейной корреляции используют коэффициент корреляции, который может быть определен по двум следующим формулам:
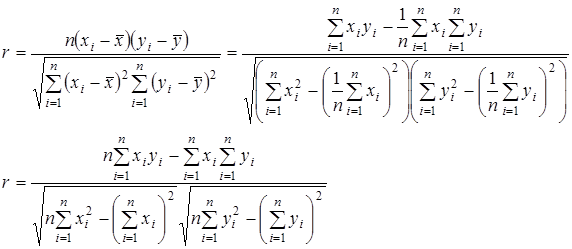 , (2.8) , (2.8)
где xi
, yi
— текущие значения случайных величин;
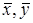 — средние значения случайных величин. — средние значения случайных величин.
Если r
= 0, то случайные величины не связаны между собой. В этом случае точки, составляющие корреляционное поле располагаются по кругу от усредняющей линии регрессии, которая параллельна оси Ох
. Если r
= 1, то имеем положительную функциональную зависимость, все точки которой принадлежат одной прямой; если r
= -1 — отрицательную. Чаще всего r
равно промежуточному значению. В этом случае между переменными существует корреляционная зависимость, а все точки располагаются в виде эллипса вокруг линии регрессии. Чем теснее связь между случайными величинами, тем ближе |
r
|
к единице.
ЗАКЛЮЧЕНИЕ
Задачей данного курсового проекта является проведение статистического анализа и прогнозирование результатов выпуска изданий (Беларуси и России).
В процессе выполнения курсового проекта мы ознакомились с основными понятиями теории вероятностей, которыми являются случайный эксперимент, события и вероятности, и математической статистики, занимающиеся восстановлением закономерностей и подчиняющие массовые однородные случайные явления на основе изучения статистических данных — результатов наблюдений; а также изучили современные методы линейного программирования и теории статистических игр.
В курсовой работе был проведен статистический анализ и прогнозирование деятельности издательств России и Беларуси с помощью следующих четырех методов:
- метод экспоненциального сглаживания;
- метод скользящего среднего;
- метод среднего темпа;
- метод Брауна.
В результате расчетов был получен прогноз деятельности издательств на 2003 год.
Из таблиц в приложениях можно сделать вывод, что метод экспоненциального сглаживания дает более точный прогноз.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Губарев А. А. Моделирование и оптимизация технологических процессов редакционно-издательских технологий. – Мн., 2005.
2. Пен Р. З. Статистические методы моделирования и оптимизации процессов целлюлозно-бумажного производства.— Красноярск, 1982.
3. Саркисяна С.А. Теория прогнозирования и принятия решений [Текст]/ Под ред. С. А. Саркисяна.— М., 1977.
4. Четыркин Е. М. Статистический метод прогнозирования.— М., 1977.
|