| Министерство образования и науки Украины
Севастопольский национальный технический университет
Факультет Экономики и менеджмента
Кафедра Финансов и кредита
МОДУЛЬ № 2
на тему: Использование эвристических и экономико-математических методов при решении задач управления
по дисциплине «Экономический анализ»
СОДЕРЖАНИЕ
1 Вводная часть
2 Расчетная часть
2.1 Решение методом экспертных оценок
2.2 Решение симплекс методом
3 Аналитическая записка
1 ВВОДНАЯ ЧАСТЬ
Целью данной работы является изучение возможностей эвристических и экономико-математических методов для принятия управленческих решений.
В данной работе были поставлены задачи, решение которых было найдено путем использования такого эвристического метода, как метода экспертных оценок, а также используя линейное прогнозирование (симплекс-метод). В первой части работы необходимо найти с помощью экспертных оценок типы сыров, которые пользуются наибольшим спросом. Именно данные метод представляет собой обобщение оценок экспертов, а особенностью метода является последовательность, индивидуальность опроса экспертов. Такая методика исключает непосредственный контакт экспертов между собой и, следовательно, групповое влияние, возникающее при совместной работе и состоящее в приспособлению к мнению большинства.
Во второй части работы (2ая и 3я задача) определить структуру комплекса оборудования и получения максимальной выгоды при наличии ограниченных исходных данных. Преимущество данного метода перед другими устанавливают, во-первых, с помощью критерия оптимальности F. Для промышленных и с\х предприятий оптимальным считается план, обеспечивающий выпуск заданного объема продукции при минимальных затратах, а также получение максимальной прибыли при ограниченном объеме ресурсов. В данном случае имеется предприятие, совокупность нового оборудовании и получение максимальной прибыли, которая должна покрыть расходы на покупку оборудования.
Объектом анализа является дальнейшее развитие деятельности предприятия по производству сыров, которое находится в данный момент в состоянии кризиса, а также оптимизация производственных процессов.
В работе была использована методика, предложенная в конспекте лекций по экономическому анализу. Расчеты были произведены с помощью программы Microsoft Exсel.
Реклама

Условие задачи: сырзавод производит 8 типов сыров. На протяжении нескольких последних лет, данное предприятие несет убытки и находится в состоянии кризиса. С целью выхода из кризиса, установлена политика выбора таких типов сыров, которые пользуются наибольшим спросом. Данные сыры будут производится, а производство сыров, которые пользуются в меньшей степени спросом, необходимо прекратить. Остатки готовой продукции сыров, которые пользуются наименьшим спросом, необходимо распродать в кратчайшие сроки.
Для осуществления поставленной цели было принято решение произвести дегустацию сыров покупателями в магазинах. По итогам дегустации был выбран 1 тип сыра, однако в связи с необходимостью выбора ещё 2 видов сыров, был произведен отбор из 7 типов сыров путем экспертных оценок. Таким образом, в 8 магазинах (8 экспертов) был произведен опрос после дегустации и были получены соответствующие оценки спроса на данные сыры. Ранги, присвоенные этим сырам, приведены ниже в таблице. Оценивание происходит по 9-бальной системе, где 9 баллов присваивается типу сыра, который пользуется наибольшим спросом, а 1 балл – наименьшим.
Таблица 1. Данные о мнениях (выставленных рангах) экспертов
| Эксперты
|
Варианты типов сыров
|
| «Дружба»
|
«Весё-лый»
|
«Лазурный»
|
«Майский»
|
«Неженка»
|
«Пупырчатый»
|
«Традици-онный»
|
| 1
|
1
|
2
|
1
|
2
|
2
|
9
|
6
|
| 2
|
2
|
4
|
2
|
3
|
2
|
7
|
5
|
| 3
|
1
|
5
|
1
|
4
|
2
|
9
|
4
|
| 4
|
2
|
4
|
2
|
3
|
3
|
8
|
6
|
| 5
|
3
|
3
|
1
|
4
|
4
|
9
|
6
|
| 6
|
1
|
5
|
3
|
4
|
4
|
7
|
5
|
| 7
|
3
|
4
|
4
|
2
|
2
|
6
|
4
|
| 8
|
1
|
3
|
1
|
3
|
4
|
9
|
5
|
После определения типов сыров, которые пользуются наименьшим спросом, предприятие решает на часть вырученных денежных средств от продажи остатков данных типов сыров закупить новое оборудование для улучшения и облегчения производства. Новое оборудование предполагается закупить в течение месяца, путем постепенного их приобретения. Предполагается, что:
- первый комплекс оборудования включает в себя: прессы сырные вертикальные - 1000 грн, кассеты для прессования полутвердых сыров - 500 грн., ванна сыродельная - 3000 грн;
- второй комплекс оборудования: прессы сырные вертикальные - 1500 грн, кассеты для прессования полутвердых сыров – 400 грн, ванна сыродельная – 4000 грн.
Исходя из распределения ресурсов, полученных от продажи остатков готовой продукции, на покупку прессов сырных вертикальных предприятие может направить 22000 т грн., на кассеты для прессования полутвердых сыров - 9000 грн, на сыродельные ванны – 56000 грн. Необходимо определить структуру оптимального комплекса оборудования и максимальную прибыль.
Реклама

Таблица 2 – Исходные данные для симплекс-метода
| |
Количество единиц, содержащихся в 1 наборе техники
|
Покупка, грн.
|
| 1 пакет
|
2 пакет
|
| Прессы сырные вертикальные
|
1
|
1,5
|
22000
|
| Кассеты для прессования полутвердых сыров
|
0,5
|
0,4
|
9000
|
| Ванна сыродельная
|
3
|
4
|
56000
|
2 РАСЧЕТНАЯ ЧАСТЬ
2.1 Решение методом экспертных оценок
Решение: был произведен отбор из 7 типов сыров путем экспертных оценок. Таким образом, в 8 магазинах (8 экспертов) после дегустации были получены соответствующие оценки спроса на данные сыры. Ранги, присвоенные этим сырам, приведены выше в условии задачи. Ниже опишем матрицу рангов ответов экспертов по 7 типам сыров в таблице. Оценивание происходит по 9бальной системе, где 9 баллов присваивается типу сыра, который пользуется наибольшим спросом, а 1 – наименьшим. Типы сыров, оцененные низшими, присваивается ранг 1, следующему 2, далее 3 и 4 и т.д. Если же эксперт поставил одинаковые баллы нескольким различным моделям, то это означает, что он присваивает им одинаковые ранги. Ответы экспертов сводятся в матрицу рангов, которая представлена в таблице 3.
Таблица 3 - Матрица рангов ответов экспертов по 7 подразделениям
| Типы сыров
|
|
|
|
Эксперты
|
|
|
|
|
| |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
| «Дружба»
|
1
|
2
|
1
|
2
|
3
|
1
|
3
|
1
|
| «Весёлый»
|
2
|
4
|
5
|
4
|
3
|
5
|
4
|
3
|
| «Лазурный»
|
1
|
2
|
1
|
2
|
1
|
3
|
4
|
1
|
| «Майский»
|
2
|
3
|
4
|
3
|
4
|
4
|
2
|
3
|
| «Неженка»
|
2
|
2
|
2
|
3
|
4
|
4
|
2
|
4
|
| «Пупырчатый»
|
9
|
7
|
9
|
8
|
9
|
7
|
6
|
9
|
| «Традиционный»
|
6
|
5
|
4
|
6
|
6
|
5
|
4
|
5
|
Таблица 4 - Матрица переранжировки рангов
| Типы сыров
|
Эксперты
|
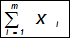
|
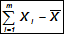
|
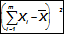
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
|
|
| 1
|
1,5
|
2
|
1,5
|
1,5
|
2,5
|
1
|
3
|
1,5
|
14,5
|
-17,5
|
306,25
|
| 2
|
4
|
5
|
6
|
5
|
2,5
|
5,5
|
5
|
3,5
|
36,5
|
4,5
|
20,25
|
| 3
|
1,5
|
2
|
1,5
|
1,5
|
1
|
2
|
5
|
1,5
|
16
|
-16
|
256
|
| 4
|
4
|
4
|
4,5
|
3,5
|
4,5
|
3,5
|
1,5
|
3,5
|
29
|
-3
|
9
|
| 5
|
4
|
2
|
3
|
3,5
|
4,5
|
3,5
|
1,5
|
5
|
27
|
-5
|
25
|
| 6
|
6
|
7
|
7
|
7
|
7
|
7
|
7
|
7
|
55
|
23
|
529
|
| 7
|
7
|
6
|
4,5
|
6
|
6
|
5,5
|
5
|
6
|
46
|
14
|
196
|
| Сумма
|
28
|
28
|
28
|
28
|
28
|
28
|
28
|
28
|
224
|
0
|
1341,5
|
Произведем переранжировку рангов и оформим в таблицу 4 (см. выше). Также в данной таблице рассчитаем среднее значение Хi по формуле
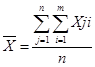
которое будет равно Хi=224/7=32; найдем значение
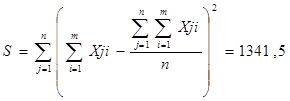
Формула коэффициента конкордации имеет вид:
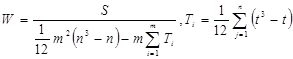
Где t - число связанных рангов в каждом отдельно взятом столбце матрицы рангов,
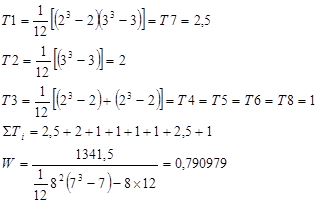
W: 0,79  0,7. В данном случае согласованность считается хорошей. 0,7. В данном случае согласованность считается хорошей.
Для определения значимости коэффициента конкордации исчисляется критерий X2
(Пирсона) с числом степеней свободы n-1:
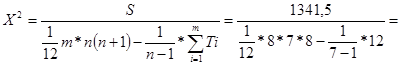 37,97 37,97
Значение X2
сравнивается с табличным X2
T
. Величина X2
должна быть больше X2
T
.
Так как X2
> X2
T
при 5%-ном уровне значимости, то нулевую гипотезу случайности совпадений мнений экспертов следует считать отвергнутой.
Построим гистограмму (рис.1):
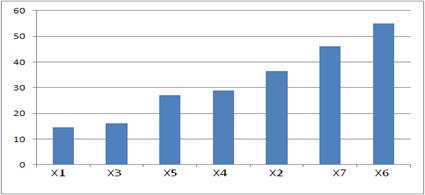
Рис.1 – Гистограмма распределения типов сыров по наличию спроса на них
Из данных рисунка 1 видно, что спрос на сыр распределяется следующим образом: Х1, Х3, Х5, Х4, Х3, Х7, Х6. Таким образом, можно сделать вывод о том, что наибольшим спросом пользуется сыр «Традиционный» и «Пупырчатый».
2 2 Решение симплекс-методом
Итак, в конечном итоге было выбрано 3 типа сыра, которые предприятие будет производить в дальнейшем. После продажи остатков оставшихся типов сыров, предприятию потребуется направить имеющиеся деньги на покупку нового оборудования для облегчения и усовершенствования производства. Напомним, что у нас имеется 2 комплекса оборудования, состоящего из 3 типов оборудования: прессы сырные вертикальные, кассеты для прессования полутвердых сыров и сыродельные ванны.
Таблица 5 – Исходные данные для симплекс-метода
| |
Количество единиц, содержащихся в 1 наборе техники
|
Покупка, грн.
|
| 1 пакет
|
2 пакет
|
| Прессы сырные вертикальные
|
1
|
1,5
|
22000
|
| Кассеты для прессования полутвердых сыров
|
0,5
|
0,4
|
9000
|
| Ванна сыродельная
|
3
|
4
|
56000
|
1)составим экономико-математическую модель задачи:
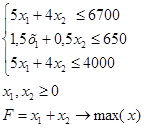
2) Составим симплекс-матрицу и определим разрешающий элемент
| |
х1
|
х2
|
Свободный член
|
Q = В/разреш столбец (-Х2
)
|
| Y1
|
1
|
1,5
|
22000
|
22000/1=22000
|
| Y2
|
0,5
|
0,4
|
9000
|
9000/0,5=18000 – минимальное
|
| Y3
|
3
|
4
|
56000
|
56000/3=18666,67
|
| F
|
-1
|
-1
|
0
|
|
Поэтапно оптимизируем симплекс-матрицы:
3) Найдем опорное и оптимальное решение, которому соответствует симплекс–таблица с неотрицательными значениями всех свободных членов в строке F. Выберем разрешающий столбец. Для этого в F-cтроке выберем наибольший по модулю отрицательный элемент столбца свободного члена (мах по модулю отрицательное):
(-С1
; -С2
) = -1;
4) Выберем разрешающую строку, найдя для этого минимальное частное от деления элементов столбца свободных членов на соответствующем им элементы, и разрешающий столбец:
Q = мин (В1
/А12
; В2
/А21..
) =18000 (В2
);
5) Найдем на пересечении разрешающего столбца и разрешающей строки разрешающий элемент -(А21
);
6) Выполним преобразование исходной симплекс-таблицы с записью результатов в новую таблицу, начиная всегда с пересчета разрешённого элемента:
А21
=1/А21
=1/0,5=2;
7) Произведем пересчет элементов разрешённой строки: А22
=А22
/А21
=0,4/1,5=0,8;
В2
=В2/А21
=9000/0,5=18000.
8) Произведем пересчет элементов разрешённого столбца А11
= -А11
/А21
= -1/0,5=-2
А31
= -А31
/А21
= -3/0,5=-6
А41
= -А41
/А21
=-( -1)/0,5=2
9) Произведем пересчет прочих элементов таблицы, внешних свободных членов и элементов F строки, которые вычисляются по правилу прямоугольника: проводится прямоугольник через элемент, подлежащий пересчету и через разрешённый элемент, и делается пересчет по формуле:
А12
= А12
– А22
*А11
/А21
=1,5-0,4*1/0,5=-7
А32
= А32
– А31
*А22
/А21
=4-3*0,4/0,5=1,6
А42
= А42
– А22
*А41
/А21
=-1-0,4*(-1)/0,5=-0,2
В1
= В1
– В2
*А11
/А21
=22000-9000*1/0,5=4000
В3
= В3
– В2
*А31
/А21
=56000-9000*3/0,5=2000
В4
= В4
– В2
*А41
/А21
=0-9000*(-1)/0,5=18000
1-е преобразование:
| |
У2
|
Х2
|
Свободный член
|
Q = В/разреш столбец (-Х1
)
|
| Y1
|
-2
|
0,7
|
4000
|
4000/0,7 =5714,286
|
| Х1
|
2
|
0,8
|
18000
|
18000/0,8= 22500
|
| У3
|
-6
|
1,6
|
2000
|
2000/1,6 = 1250 – минимальное
|
| F
|
2
|
-0,2
|
18000
|
|
Т.к. матрица описывает не оптимальный план (в F-строке есть отрицательный элемент), то есть возможность увеличить целевую функцию). Этапы оптимизации такие же, как и в первом преобразовании.
2-е преобразование (последнее):
| |
У2
|
У3
|
Свободный член
|
| У1
|
0,625
|
-0,4375
|
3125
|
| х1
|
5
|
-0,5
|
17000
|
| Х2
|
-3,75
|
0,625
|
1250
|
| F
|
1,25
|
8
|
18250
|
Поскольку в строке целевой функции больше нет отрицательных элементов, можно говорить о том, что план оптимален и соответствует максимальному значению целевой функции при существующих ограничениях в ресурсах.
3 АНАЛИТИЧЕСКАЯ ЗАПИСКА
Таким образом, путем различных преобразований, используя различные экономико-математические методы, пришли к следующему выводу. Перед предприятием по производству сыра была поставлена цель определения типов сыров, которые пользуются наибольшим спросом. Выбор необходимо было сделать между 8 типами сыров. После выбора «победителя» дегустации путем экспертных оценок были определены ещё 2 типа сыров, которые пользуются наивысшим спросом. Такими сырами стали «Традиционный» и «Пупырчатый». Производство остальных сыров («Дружба», «Весёлый», «Лазурный», «Майский» и «Неженка») прекращено.
Также были поставлены задачи по определению максимальной прибыли при использовании определенного комплекса нового оборудования, а также структуры покупки нового оборудования, имея данные о стоимости оборудования, а также об отчислениях на закупку различных комплексов оборудования по различной цене.
После двух преобразований, используя симплекс-метод (линейное программирование), была получена оптимальная (итоговая) симплекс-таблица. По полученным данным можно сделать следующий вывод, что структура оптимальной закупки нового оборудования будет включать покупку первого и второго комплекса оборудования. При этом ресурсы, которые были направлены на покупку вертикальных сырных прессов, кассетов для прессования полутвердых сыров и сыродельных ванн расходуются полностью.
| |
У2
|
У3
|
Свободный член
|
|
| У1
|
0,625
|
-0,4375
|
3125
|
Остаток средств при покупке вертикальных сырных прессов
|
| х1
|
5
|
-0,5
|
17000
|
Комплекс оборудования 1
|
| Х2
|
-3,75
|
0,625
|
1250
|
Комплекс оборудования 2
|
| F
|
1,25
|
8
|
18250
|
|
Остаток средств при покупке вертикальных сырных прессов составит 1250 грн. Максимально возможная прибыль будет равна 18250 грн. Следовательно, можно сказать, что предприятию необходимо в кратчайшие сроки продать остатки продукции, которые в меньшей степени пользуются спросом, чтобы на вырученные деньги закупить новое оборудование и повысить качество продукции, ускорить процесс производства, чтобы покрыть убытки от закупки новых комплексов оборудования.
Все поставленные задачи можно считать решенными. Правильность их решения была проверена по средствам программ: Microsoft Exсel и SIMP.EXE.
|