Северская Государственная Технологическая Академия
Имитационное структурное моделирование системы ЭП
на ЦВМ с учетом нелинейностей
Северск
200
8
Цель работы
Методом цифрового имитационного моделирования исследовать переходные процессы в элементах электропривода и автоматической системе регулирования с учетом влияния нелинейного момента нагрузки.
Структурная и функциональная схемы системы

Рис. 1 – Функциональная схема системы “ЭМУ – Д”

Рис. 2 – Структурная схема системы “ЭМУ – Д”
Технические данные
Данные для расчета представлены в таблице 1.
Таблица 1 – Данные для расчета
| ЭМУ |
Двигатель |
ТГ |
| Еэму
|
К1
|
Ту
|
К2
|
Ткз
|
Rя эму
|
Uн
|
I |
wн
|
Rяц
|
Тяц
|
Тэм
|
Ктг
|
| В |
- |
с |
- |
с |
Ом |
В |
А |
рад/с |
Ом |
с |
с |
В×с |
| 230 |
1,5 |
0,05 |
1,5 |
0,17 |
5,3 |
220 |
4,25 |
157 |
2,9 |
0,02 |
0,18 |
1 |
Нелинейная зависимость момента сопротивления механизма приведена на рис. 3.
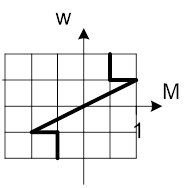
Рис. 3 - Нелинейная зависимость момента сопротивления механизма
Краткое описание этапов и особенностей процесса моделирования
На первом этапе необходимо оценить все возможные алгоритмы функционирования системы и выбрать наиболее полно отвечающий цели моделирования. Этот этап заканчивается принятием допущений и оценкой ограничений для процесса моделирования.
Второй этап подразумевает создание математических моделей системы и окружающей среды с учетом результатов и выводов первого этапа, причем, математические модели могут содержать взаимосвязанные подсистемы и элементы.
Третий этап содержит выбор способа решения уравнений математической модели. Затем разрабатывается алгоритм решения задачи и пишется программа на выбранном языке (PASCAL).
Заключительный, четвертый этап содержит отладку программы. Ввод данных, непосредственное решение задачи, вывод и анализ результатов.
Составление математической модели для системы “ЭМУ – Д”
На схеме (рис. 2) ЭМУ представлен в виде двух апериодических звеньев с коэффициентами К1
первого и К2
второго каскадов усиления и постоянными времени Ту
обмотки управления и Ткз
короткозамкнутой обмотки. Структурная схема двигателя состоит из безинерционного, интегрирующего и апериодического звеньев, параметры которых определяются сопротивлением якорной цепи Rяц
, электромагнитной – Тяц
и электромеханической – Тэм
постоянными времени, а коэффициент передачи безинерционного звена С рассчитывается по номинальным данным двигателя.
Определяем величину сигнала ошибки на входе системы:
Реклама

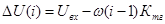
Для получения частного решения численным методом, например, Эйлера первого порядка необходимы конечно-разностные уравнения. Удобнее всего осуществить переход от передаточной функции звена к конечно-разностному уравнению.
В результате перехода к конечно-разностным уравнениям получим уравнения для пошагового машинного решения численным методом Эйлера первого порядка для апериодических звеньев:
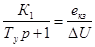 ,
, 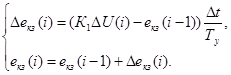
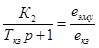 ,
, 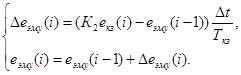
Находим ЭДС управления еу
на втором сумматоре схемы:
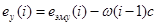 .
.
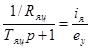 ,
, 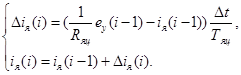
Моделирование нелинейного момента сопротивления механизма из-за трудоемкости описания его дифференциальными уравнениями проведем с использованием логических зависимостей:
– при пуске:
если 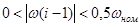 , то , то 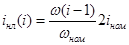 ; ;
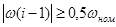 , то , то 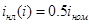
Определим величину суммарного тока на третьем сумматоре схемы:
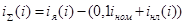 .
.
В результате перехода к конечно-разностным уравнениям получим уравнения для пошагового машинного решения численным методом Эйлера первого порядка для интегрирующего звена:
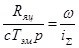 ,
, 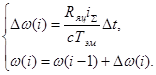
Алгоритм расчета переходных процессов в системе “ЭМУ – Д”
Выражения, приведенные в пункте 5, являются исходными для составления алгоритма решения задачи, в котором предусмотрено конечное время расчета переходного процесса tпп
с шагом интегрирования Dt.
Алгоритм, представленный на рис. 3, соответствует пуску ДПТ при нелинейном моменте сопротивления механизма.
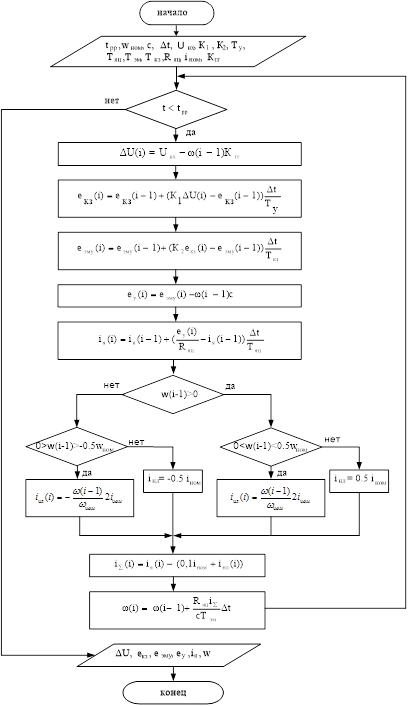
Рис. 4 – Алгоритм расчета переходных процессов в системе “ЭМУ – Д”
Листинг программ расчета и графики переходных процессов
Пуск ДПТ при линейном моменте сопротивления механизма
program map;
uses graph;
var
wnom,t,eu,Uvx,Tac,inl,ic,isum,inom,ia,w,k1,k2,ktg,du,ekz,emu,dt,
tpp,rc,Tu,Tkz,c,Tem:real;
x,y,gd,gm:integer;
begin
tpp:=12;
wnom:=157;
c:=1.322;
dt:=0.001;
Uvx:=10;
k1:=1.5;
k2:=1.5;
Tu:=0.05;
Tkz:=0.17;
rc:=5.3;
inom:=4.25;
Tac:=0.02;
Tem:=0.18;
ktg:=1;
w:=0;
gd:=vga;initgraph(gd,gm,'c:\BPascal\BGI');
setlinestyle(1,0,1);setcolor(2);
for x:=0 to 9 do
line(x*70,0,x*70,199);
for y:=0 to 9 do
line(0,y*20,639,y*20);
setcolor(5);
setlinestyle(0,0,1);setcolor(6);
line(0,120,639,120);
line(70,0,70,199);
setcolor(4); outtextxy(10,10,'w,rad/sec ');
setcolor(4); outtextxy(90,10,'Isum,A');
setcolor(4); outtextxy(580,125,'t,sec');
setcolor(7); outtextxy(120,125,'1,5 3.0 4.5 6.0 7.5 9.0');
setcolor(7); outtextxy(40,100,'4,0');
setcolor(7); outtextxy(40,80,'8,0');
setcolor(7); outtextxy(40,60,'12,0');setcolor(7); outtextxy(40,40,'16,0');
ic:=0.1*inom;
while t<tpp do
begin
du:=Uvx-w*ktg;
ekz:=ekz+(k1*du-ekz)*(dt/Tu);
emu:=emu+(k2*ekz-emu)*(dt/Tkz);
eu:=emu-w*c;
ia:=ia+((eu/rc)-ia)*(dt/Tac);
Реклама

isum:=ia-ic;
w:=w+((rc*isum*dt)/(c*Tem));
t:=t+dt;
putpixel(round(70+t*700/tpp),round(120-w*5),1);
putpixel(round(70+t*700/tpp),round(120-Isum*5),4);
end;
readln;
closegraph;
writeln('Pusk DPT pri lineinom momente soprotivleniya');
writeln('');
writeln('Chastota vrasheniya w=',w:6:2);
writeln('Tok yakorya ia:=',ia:4:2);
writeln('Signal oshibki dU=',ia:4:2);
writeln('EDS kz Ekz=',ekz:6:2);
writeln('EDS emu Emu=',emu:6:2);
writeln('EDS oy Ey=',eu:4:2);
writeln('isum=',isum:4:2);
readln;
end.
Пуск ДПТ при нелинейном моменте сопротивления механизма
program map;
uses graph;
var
wnom,t,eu,Uvx,Tac,inl,ic,isum,inom,ia,w,k1,k2,ktg,du,ekz,emu,dt,
tpp,rc,Tu,Tkz,c,Tem,inel:real;
x,y,gd,gm:integer;
begin
gd:=vga;initgraph(gd,gm,'c:\BPascal\BGI');
tpp:=2;
wnom:=157;
c:=1.322;
dt:=0.001;
Uvx:=10;
k1:=1.5;
k2:=1.5;
Tu:=0.05;
Tkz:=0.17;
rc:=5.3;
inom:=4.25;
Tac:=0.02;
Tem:=0.18;
ktg:=1;
w:=0;
setlinestyle(1,0,1);setcolor(2);
for x:=0 to 9 do
line(x*70,0,x*70,199);
for y:=0 to 9 do
line(0,y*20,639,y*20);
setcolor(5);
setlinestyle(0,0,1);setcolor(6);
line(0,120,639,120);
line(70,0,70,199);
setcolor(4); outtextxy(10,10,'w,rad/sec ');
setcolor(4); outtextxy(90,10,'Isum,A');
setcolor(4); outtextxy(580,125,'t,sec');
setcolor(7); outtextxy(120,125,'6,0 12.0 18.0 24.0 30.0 36.0 42.0 48.0');
ic:=0.1*inom;
while t<tpp do
begin
du:=Uvx-w*ktg;
ekz:=ekz+(k1*du-ekz)*(dt/Tu);
emu:=emu+(k2*ekz-emu)*(dt/Tkz);
eu:=emu-w*c;
if 0<w<0.5*wnom THEN inel:=(w/wnom)*2*inom; if w>0.5*wnom THEN inel:=0.5*inom;
isum:=ia-(ic+inel);
w:=w+((rc*isum*dt)/(c*Tem));
t:=t+dt;
putpixel(round(70+t*700/tpp),round(120-w*0.100),1);
putpixel(round(70+t*700/tpp),round(120-isum*9),4);
end;
readln;
closegraph;
writeln('Pusk DPT pri nelineinom momente soprotivleniya');
writeln('');
writeln('Chastota vrasheniya w=',w:6:2);
writeln('Tok yakorya ia:=',ia:4:2);
writeln('Signal oshibki dU=',ia:4:2);
writeln('EDS kz Ekz=',ekz:6:2);
writeln('EDS emu Emu=',emu:6:2);
writeln('EDS oy Ey=',eu:4:2);
writeln('isum=',isum:4:2);
readln;
end.
Результаты программы расчета переходных процессов в системе “ЭМУ-Д”
Пуск ДПТ при линейном моменте нагрузки:
W=51 с-1
, ia
=0,44 А, dU=32.17 B, Ekz
=48.28 B, Emu
=72.55 B, Ey
=1.26 B, isum
=0.02 A
Пуск ДПТ при нелинейном моменте нагрузки:
W=54.4 с-1
, ia
=2,20 А, dU=31.8 B, Ekz
=50.78 B, Emu
=81.12 B, Ey
=4.86 B, isum
=0.02 A
|