Содержание
Введение
Глава1.
Моделирование систем массового обслуживания
1.1.
Структура и параметры эффективности и качества функционирования СМО
1.2 Классификация СМО и их основные элементы
1.3 Процесс имитационного моделирования
Глава 2. Распределения и генераторы псевдослучайных чисел
2.1 Виды распределений
2.2 Виды генераторов случайных чисел
Глава 3. Практическая часть
3.1 Постановка задачи
3.2 Описание метода решения задачи вручную
3.3 Блок-схема
3.4 Перевод модели на язык программирования
Заключение
Список использованной литературы
ВВЕДЕНИЕ
Во многих областях практической деятельности человека мы сталкиваемся с необходимостью пребывания в состоянии ожидания. Подобные ситуации возникают в очередях в билетных кассах, в крупных аэропортах, при ожидании обслуживающим персоналом самолетов разрешения на взлет или посадку, на телефонных станциях в ожидании освобождения линии абонента, в ремонтных цехах в ожидании ремонта станков и оборудования, на складах снабженческо-сбытовых организ
аций в ожидании разгрузки или погрузки транспортных средств. Во всех перечисленных случаях имеем дело с массовостью и обслуживанием. Из
учением таких ситуаций з
анимается теория массового обслуживания.
В теории систем массового обслуживания (в дальнейшем просто – CMО) обслуживаемый объект называют требованием.
В общем случае под требованием обычно понимают з
апрос на удовлетворение некоторой потребности, например, обслуживание автомобиля на заправочной станции, раз
говор с абонентом, посадка самолета, покупка билета, получение материалов на складе и т.д
На первичное развитие теории массового обслуживания оказали особое влияние работы датского ученого А.К. Эрланга (1878-1929).
Теория массового обслуживания
– область прикладной математики, занимающаяся анализом процессов в системах производства, обслуживания, управления, в которых однородные события повторяются многократно, например, на предприятиях бытового обслуживания; в системах приема, переработки и передачи информации; автоматических линиях производства и др.
Задача теории массового обслуживания
– установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных показателей (количества каналов в системе, параметров входящего потока заявок и т.д.). Результирующими показателями или интересующими нас характеристиками СМО являются – показатели эффективности СМО, которые описывают способна ли данная система справляться с потоком заявок.
Реклама

В теории СМО
рассматриваются такие случаи, когда поступление требований происходит через случайные промежутки времени, а продолжительность обслуживания требований не является постоянной, т.е. носит случайный характер. В силу этих причин одним из
основных методов математического описания СМО является аппарат теории случайных проц
ессов .
Основной задачей теории СМО является изучение режима функционирования обслуживающей системы и исследование явлений, возникающих в процессе обслуживания. Так, одной из
характеристик обслуживающей системы является время пребывания требования в очереди. Очевидно, что это время можно сократить з
а счет увеличения количества обслуживающих устройств. Однако каждое дополнительное устройство требует определенных материальных затрат, при этом увеличивается время бездействия обслуживающего устройства из-з
а отсут
ствия требований на обслуживание, что также является негативным явлением. Следовательно, в теории СМО воз
никают з
адачи оптимизации:
каким образ
ом достичь определенного уровня обслуживания (максимального сокращения очереди или потерь требований) при минимальных затратах, связанных с простоем обслуживающих ус
тройств.
Имитационное моделирование реализуются программно с использованием различных языков, как универсальных - БЕЙСИК, РАСКАЛЬ, СИ и т.д., так и специализированных, предназначенных для построения имитационных моделей - СИМСКРИПТ, СТАМ/КЛАСС, GPSS, SLAM, Pilgrim и др.
Цель курсовой работы по дисциплине «Имитационное моделирование экономических процессов» - ознакомление с современными концепциями построения моделирующих систем, с основными приемами имитационного моделирования, встраиваемыми в общую процедуру преобразования информации от структурирования и формализации составляющих предметных областей до интерпретации обработанных данных и приобретенных знаний, связанных с описанием экономических процессов.
Данная работа представляет собой работу по созданию и реализации математической модели системы массового обслуживания для получения необходимых нам результатов на основании исходных данных и известных математических зависимостей. Целью данной курсовой работы является анализ и моделирование работы станции технического обслуживания, создав программу на языке С++, имитирующую ее работу; сравнение полученных результатов моделирующей программы с результатами работы реального объекта.
Реклама

Глава 1. Моделирование систем массового обслуживания
1.1.
Структура и параметры эффективности и качества функционирования СМО
Многие экономические задачи связаны с системами массового обслуживания, т.е. такими системами, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо услуг, с другой – происходит удовлетворение этих запросов. СМО включает в себя следующие элементы: источник требований, входящий поток требований, очередь, обслуживающие устройства (каналы обслуживания), выходящий поток требований. Исследованием таких систем занимается теория массового обслуживания.
Средства, обслуживающие требования, называются
обслуживающими устройствами или каналами обслужи
вания. Например, к ним относятся заправочные устройства на АЗС, каналы телефонной связи, посадочные полосы, мастера-ремонтники, билетные кассиры, погрузочно-разгрузочные точки
на базах и складах.
Методами теории массового обслуживания могут быть решены многие задачи исследования процессов, происходящих в экономике. Так, в организации торговли эти методы позволяют определить оптимальное количество торговых точек данного профиля, численность продавцов, частоту завоза товаров и другие параметры. Другим характерным примером систем массового обслуживания могут служить заправочные станции, и задачи теории массового обслуживания в данном случае сводятся к тому, чтобы установить оптимальное соотношение между числом поступающих на заправочную станцию требований на обслуживание и числом обслуживающих устройств, при котором суммарные расходы на обслуживания и убытки от простоя были бы минимальными. Теория массового обслуживания может найти применение и при расчете площади складских помещений, при этом складская площадь рассматривается как обслуживающее устройство, а прибытие транспортных средств под выгрузку – как требование. Модели теории массового обслуживания применяются также при решении ряда задач организации и нормирования труда, других социально-экономических проблем.
Каждая СМО включает в свою структуру некоторое число обслуживающих устройств, называемых каналами обслуживания (к их числу можно отнести лиц, выполняющих те или иные операции, - кассиров, операторов, менеджеров, и т.п.), обслуживающих некоторый поток заявок (требований), поступающих на ее вход в случайные моменты времени. Обслуживание заявок происходит за неизвестное, обычно случайное время и зависит от множества самых разнообразных факторов. После обслуживания заявки канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времени их обслуживания приводит к неравномерности загрузки СМО - перегрузке с образованием очередей заявок или недогрузке - с простаиванием ее каналов. Случайность характера потока заявок и длительности их обслуживания порождает в СМО случайный процесс, для изучения которого необходимы построение и анализ его математической модели. Изучение функционирования СМО упрощается, если случайный процесс является марковским (процессом без последействия, или без памяти), когда работа СМО легко описывается с помощью конечных систем обыкновенных линейных дифференциальных уравнений первого порядка, а в предельном режиме (при достаточно длительном функционировании СМО) посредством конечных систем линейных алгебраических уравнений. В итоге показатели эффективности функционирования СМО выражаются через параметры СМО, потока заявок и дисциплины.
Из теории известно, чтобы случайный процесс являлся Марковским, необходимо и достаточно, чтобы все потоки событий (потоки заявок, потоки обслуживаний заявок и др.), под воздействием которых происходят переходы системы из состояния в состояние, являлись пуассоновским, т.е. обладали свойствами последствия (для любых двух непересекающихся промежутков времени число событий, наступающих за один из них, не зависит от числа событий, наступающих за другой) и ординарности (вероятность наступления за элементарным, или малый, промежуток времени более одного события пренебрежимо мала по сравнению с вероятностью наступления за этот промежуток времени одного события). Для простейшего пуассоновского потока случайная величина Т (промежуток времени между двумя соседними событиями) распределена по показательному закону, представляя собой плотность ее распределения или дифференциальную функцию распределения.
Если же в СМО характер потоков отличен от пуассоновского, то ее характеристики эффективности можно определить приближенно с помощью Марковской теории массового обслуживания, причем тем точнее, чем сложнее СМО, чем больше в ней каналов обслуживания. В большинстве случаев для обоснованных рекомендаций по практическому управлению СМО совсем не требует знаний точных ее характеристик, вполне достаточно иметь их приближенные значения.
Каждая СМО в зависимости от своих параметров обладает определенной эффективностью функционирования.
Эффективность функционирования СМО характеризуют три основные группы показателей:
1. Эффективность использования СМО – абсолютная или относительная пропускные способности, средняя продолжительность периода занятости СМО, коэффициент использования СМО, коэффициент не использования СМО;
2. Качество обслуживания заявок- среднее время (среднее число заявок, закон распределения) ожидания заявки в очереди или пребывания заявки в СМО; вероятность того, что поступившая заявка немедленно примется к исполнению;
3. Эффективность функционирования пары CМО потребитель, причем под потребителем понимается как совокупность заявок или их некоторый источник (например, средний доход, приносимый СМО за единицу времени эксплуатации, и др).
1.2 Классификация СМО и их основные элементы
СМО классифицируются на разные группы в зависимости от состава и от времени пребывания в очереди до начала обслуживания, и от дисциплины обслуживания требований.
По состав
у
СМО бывают одноканальные
(с одним обслуживающим уст
ройством) и многоканальные
(с большим числом обслуживающих устройств).
Многоканальные системы могут состоят
ь из обслужива
ющих устройств как одинаковой, так и разной производительности.
По времени пребывания требований в очереди до начала обслуживания системы
делятся на три группы:
1) с неограниченным временем ожидания (с ожиданием),
2) с отказами;
3) смешанного типа.
В СМО с неограниченным временем ожидания
очередное требование, застав все устройства занятыми, становится в очередь и ожидает обслуживания до тех пор, пока одно из устройств не освободится.
В системах с отказами поступившее требование, застав все устройства занятыми, покидает систему. Классическим примером системы с отказами может служить работа автоматической телефонной станции.
В системах смешанного типа поступившее требование, застав все (устройства занятыми, становятся в очередь и ожидают обслуживания в течение ограниченного времени. Не дождавшись обслуживания в установленное время, требование покидает систему.
Кратко рассмотрим особенности функционирования некоторых из этих ситем.
1. СМО с ожиданием
характеризуется тем, что в системе из n (n>=1) любая заявка, поступившая в СМО в момент, когда все каналы заняты, становится в очередь и ожидает своего обслуживания, причем любая пришедшая заявка обслужена. Такая система может находится в одном из бесконечного множества состояний:
sn
+к
(
r
=1.2…) –
все каналы заняты и в очереди находится r заявок.
2. СМО с ожиданием и ограничением на длину очереди
отличается от вышеприведенной тем, что эта система может находиться в одном из n+m+1 состояний. В состояниях s0
,s1
,…, sn
очереди не существует, так как заявок в системе или нет или нет вообще и каналы свободны (s0
), или в системе есть несколько I (I=1,n) заявок, которого обслуживает соответствующее (n+1, n+2,…n+r,…,n+m) число заявок и (1,2,…r,…,m) заявок , стоящих в очереди. Заявка, пришедшая на вход СМО в момент времени, когда в очереди стоят уже m заявок, получает отказ и покидает систему необслуженной.
Т.о, многоканальная СМО работает по сути как одноканальная, когда все nканалов работают как один с дисциплиной взаимопомощи, называемой все как один, но с более высокой интенсивностью обслуживания. Граф состояний подобной подобной системы содержит всего два состояния: s0
(s1
)- все n каналов свободны (заняты).
Анализ различных видов СМО с взаимопомощью типа все как один показывает, что такая взаимопомощь сокращает среднее время пребывания заявки в системе, но ухудшает ряд других таких характеристик, как вероятность отказа, пропускная способность, средние число заявок в очереди и время ожидания их выполнения. Поэтому для улучшения этих показателей используется изменение дисциплины обслуживания заявок с равномерной взаимопомощью между каналами следующим образом:
· Если заявка поступает в СМО в момент времени, когда все каналы свободны, то все n каналов приступает к ее обслуживанию;
· Если в это время приходит следующая заявка, то часть каналов переключается на ее обслуживание
· Если во время обслуживания этих двух заявок поступает третья заявка, то часть каналов переключается на обслуживание этой третьей заявки, до тех пор, пока каждая заявка, находящаяся в СМО, не окажется под обслуживанием только одного канала. При этом заявка, поступившая в момент занятости всех каналов, в СМО с отказами и равномерной взаимопомощью между каналами, может получить отказ и вынуждена будет покинуть систему необслуженной.
Методы и модели, применяющиеся в теории массового обслуживания, можно условно разделить на аналитические и имитационные.
Аналитические методы
теории массового обслуживания позволяют получить характеристики системы как некоторые функции параметров ее функционирования. Благодаря этому появляется возможность проводить качественный анализ влияния отдельных факторов на эффективность работы СМО. Имитационные методы основаны на моделировании процессов массового обслуживания на ЭВМ и применяются, если невозможно применение аналитических моделей.
В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач массового обслуживания, в которых входящий поток требований является простейшим
(пуассоновским
).
Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, т.е. вероятность поступления за время t ровно k требований задается формулой:
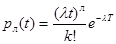
Важная характеристика СМО - время обслуживания требований в системе. Время обслуживания одного требования является, как правило, случайной величиной и, следовательно, может быть описано законом распределения. Наибольшее распространение в теории и особенно в практических приложениях получил экспоненциальный закон распределения времени обслуживания.
Функция распределения для этого закона имеет вид:
F(t)=1e-
µ
t
Т.е. вероятность того, что время обслуживания не превосходит некоторой величины t, определяется этой формулой, где µ- параметр экспоненциального обслуживания требований в системе, т.е. величина, обратная времени обслуживания tоб
:
µ=1/ tоб
Рассмотрим аналитические модели наиболее распространенных СМО с ожиданием, т.е. таких СМО, в которых требования, поступившие в момент, когда все обслуживающие каналы заняты, ставятся в очередь и обслуживаются по мере освобождения каналов.
Общая постановка задачи состоит в следующем. Система имеет n обслуживающих каналов, каждый из которых может одновременно обслуживать только одно требование.
В систему поступает простейший (пауссоновский) поток требований c параметром 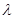 . Если в момент поступления очередного требования в системе на обслуживании уже находится не меньше n требований (т.е. все каналы заняты), то это требование становится в очередь и ждет начала обслуживания. . Если в момент поступления очередного требования в системе на обслуживании уже находится не меньше n требований (т.е. все каналы заняты), то это требование становится в очередь и ждет начала обслуживания.
В системах с определенной дисциплиной обслуживания
поступившее требование, застав все устройства занятыми, в зависимости от своего приоритета, либо обслуживается вне очереди, либо становится в очередь.
Основными элементами СМО являются:входящий поток требований, очередь требований, обслуживающие устройства, (каналы) и выходящий поток требований.
Изучение СМО начинается с анализа входящего потока требований. Входящий поток требований представляет собой совокупность требований, которые поступают в систему и нуждаются в обслуживании. Входящий поток требований изучается с целью установления закономерностей этого потока и дальнейшего улучшения качества обслуживания.
В большинстве случаев входящий поток неуправляем и зависит от ряда случайных факторов. Число требований, поступающих в единицу времени, случайная величина. Случайной величиной является также интервал времени между соседними поступающими требованиями. Однако среднее количество требований, поступивших в единицу времени, и средний интервал времени между соседними поступающими требованиями предполагаются заданными.
Среднее число требований, поступающих в систему обслуживания за единицу времени, называется интенсивностью поступл
ения требо
ваний
и
определяется следующим соотношением:
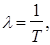
где Т
-
среднее значение интервала между поступлением очередных требований.
Для многих реальных процессов поток требований достаточно хорошо описывается законом распределения Пуассона. Такой пот
ок называется простейшим.
Простейший поток обладает
такими важными свойствами:
1)
Свойством стационарности,
которое выражает неизмен
ность вероятностного режима потока по времени. Это значит, что чис
ло т
ребований, поступающих в систему в равные промежутки времени, в среднем должно быть постоянным. Например, число вагонов, поступающих под погруз
ку в среднем в сутки должно быть одинаковым для различных периодов времени, к примеру, в начале и в конце декады.
2)
Отсутствия последействия,
которое обуславливает взаимную независимость поступления того или иного числа требований на обслуживание в непересекающиеся промежутки времени. Это значит, что число требований, поступающих в данный отрезок времени, не зависит от числа требований, обслуженных в предыдущем промежутке времени. Например, число автомобилей, прибывших за материалами в десятый день месяца, не зависит от числа автомобилей, обслуженных в четвертый или любой другой предыдущий день данного месяца.
3)
Свойством ординарности, которое выражает практическую невозможность одновременного поступления двух или более требований (вероятность такого события неизмеримо мала по отношению к рассматриваемому промежутку времени, когда последний устремляют к нулю).
При простейшем потоке требований распределение требований, поступающих в систему подчиняются закону распределения Пуассона:
вероятность 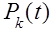 того, что в обслуживающую систему за время t поступит именно k
требований: того, что в обслуживающую систему за время t поступит именно k
требований:
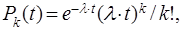
где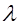 . -
среднее число требований, поступивших на обслуживание в единицу времени. . -
среднее число требований, поступивших на обслуживание в единицу времени.
На практике условия простейшего потока не всегда строго выполняются. Часто имеет место нестационарность процесса (в различные часы дня и различные дни месяца поток требований может меняться, он может быть интенсивнее утром или в последние дни месяца). Существует также наличие последействия, когда количество требований на отпуск товаров в конце месяца зависит от их удовлетворения в начале месяца. Наблюдается и явление неоднородности, когда несколько клиентов одновременно пребывают на склад за материалами. Однако в целом пуассоновский закон распределения с достаточно высоким приближением отражает многие процессы массового обслуживания.
Кроме того, наличие пуассоновского потока требований можно определить статистической обработкой данных о поступлении требований на обслуживание. Одним из признаков з
акона распределени
я Пуассона является равенство математического ожидания случайной величин
ы и дисперсии этой же величины, т.е.
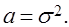
Одной из важнейших характеристик обслуживающих устройств, которая определяет пропускную способность всей системы, является время
обслуживания.
Время обслуживания одного требования (
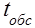 )-
случайная величина, которая может изменятся в большом диапазоне. Она зависит от стабильности работы самих обслуживающих устройств, так и от различных параметров, поступающих в систему, требований (к примеру, различной грузоподъемности транспортных средств, поступающих под погрузку или выгрузку.
)-
случайная величина, которая может изменятся в большом диапазоне. Она зависит от стабильности работы самих обслуживающих устройств, так и от различных параметров, поступающих в систему, требований (к примеру, различной грузоподъемности транспортных средств, поступающих под погрузку или выгрузку.
Случайная величина 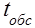 полностью характеризуется законом распределения, который определяется на основе статистических испытаний.
полностью характеризуется законом распределения, который определяется на основе статистических испытаний.
На практике чаще всего принимают гипотезу о показательном законе распределения
времени обслуживания.
Показательный закон распределения времени обслуживания имеет место тогда, когда плотность распределения резко убывает с возрастанием времени t. Например, когда основная масса требований обслуживается быстро, а продолжительное обслуживание встречается редко. Наличие показательного закона распределения времени обслуживания устанавливается на основе статистических наблюдений.
При показательном законе распределения времени обслуживания вероятность 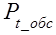 события, что время обслуживания продлиться не более чем t, равна: события, что время обслуживания продлиться не более чем t, равна:
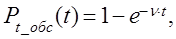
где v
- интенсивность обслуживания одного требования одним обслуживающим устройством, которая определяется из соотношения:
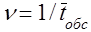 , (1) , (1)
где 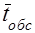  -
среднее время обслуживания одного требования одним обслуживающим устройством. -
среднее время обслуживания одного требования одним обслуживающим устройством.
Следует заметить, что если закон распределения времени обслуживания показательный, то при наличии нескольких обслуживающих устройств одинаковой мощности закон распределения времени обслуживания несколькими устройствами будет также показательным:
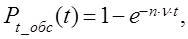
где n - количество обслуживающих устройств.
Важным параметром СМО является коэффициент загрузки 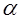 ,
который определяется как отношение интенсивности поступления требований ,
который определяется как отношение интенсивности поступления требований 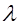 к интенсивности обслуживания v. к интенсивности обслуживания v.
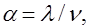 (2)
(2)
где a
-
коэффициент загрузки; 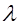 -
интенсивность поступления требований в систему; v
-
интенсивность обслуживания одного требования одним обслуживающим устройством. -
интенсивность поступления требований в систему; v
-
интенсивность обслуживания одного требования одним обслуживающим устройством.
Из (1) и (2) получаем, что
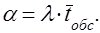
Учитывая, что 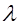 -
интенсивность поступления требований в систему в единицу времени, произведение -
интенсивность поступления требований в систему в единицу времени, произведение 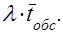 показывает количество требований, поступающих в систему обслуживания за среднее время обслуживания одного требования одним устройством.
показывает количество требований, поступающих в систему обслуживания за среднее время обслуживания одного требования одним устройством.
Для СМО с ожиданием количество обслуживаемых устройств п должно быть строго больше коэффициента загрузки (требование установившегося
или стационарного режима работы
СМО) :
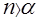 . .
В противном случае число поступающих требований будет больше суммарной производительности всех обслуживающих устройств, и очередь будет неограниченно расти.
Для СМО с отказами и смешанного типа это условие может быть ослаблено, для эффективной работы этих типов СМО достаточно потребовать, чтобы минимальное количество обслуживаемых устройств n было не меньше коэффициента загрузки 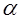 : : 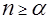
1.3 Процесс имитационного моделирования
Как уже было отмечено ранее, процесс последовательной разработки имитационной модели начинается с создания простой модели, которая затем постепенно усложняется в соответствии с требованиями, предъявляемыми решаемой проблемой. В процессе имитационного моделирования можно выделить следующие основные этапы:
1.
Формирование проблемы
: описание исследуемой проблемы и определение целей исследования.
2.
Разработка модели:
логико-математическое описание моделируемой системы в соответствии с формулировкой проблемы.
3.
Подготовка данных:
идентификация, спецификация и сбор данных.
4.
Трансляция модели:
перевод модели на язык, приемлемый для используемой ЭВМ.
5.
Верификация:
установление правильности машинных программ.
6.
Валидация:
оценка требуемой точности и соответствие имитационной модели реальной системе.
7.
Стратегическое и тактическое планирование:
определение условий проведения машинного эксперимента с имитационной моделью.
8.
Экспериментирование:
прогон имитационной модели на ЭВМ для получения требуемой информации.
9.
Анализ результатов:
изучение результатов имитационного эксперимента для подготовки выводов и рекомендаций по решению проблемы.
10.
Реализация и документирование:
реализация рекомендаций, полученных на основе имитации, составление документации по модели и ее использованию.
Рассмотрим основные этапы имитационного моделирования. Первой задачей имитационного исследования является точное определение проблемы и детальная формулировка целей исследования. Как правило, определение проблемы является непрерывным процессом , который обычно осуществляется в течении всего исследования. Оно пересматривается по мере более глубокого понимания исследуемой проблемы и возникновения новых ее аспектов.
Как только сформулировано начальное определение проблемы, начинается этап построения модели исследуемой системы. Модель включает статистическое и динамическое описание системы. В статистическом описании определяются элементы системы и их характеристики, а в динамическом- взаимодействие элементов системы, в результате которых происходит изменение ее состояния во времени.
Процесс формирования модели во многом является искусством. Разработчик модели должен понять структуру системы, выявить правила ее функционирования и суметь выделить в них самое существенное, исключив ненужные детали. Модель должна быть простой для понимания и в то же время достаточно сложной, чтобы реалистично отображать характерные черты реальной системы. Наиболее важными являются принимаемые разработчиком решения относительно того, верны ли принятые упрощения и допущения, какие элементы и взаимодействия между ними должны быть включены в модель. Уровень детализации модели зависит от целей ее создания. Необходимо рассматривать только те элементы, которые имеют существенное значение для решения исследуемой проблемы. Как на этапе формирования проблемы, так и на этапе моделирования необходимо тесное взаимодействие между разработчиком модели и ее пользователями. Кроме того, тесное взаимодействие на этапах формулирования проблемы и разработки модели создает у пользователя уверенность в правильности модели, поэтому помогает обеспечить успешную реализацию результатов имитационного исследования.
На этапе разработки модели определяются требования к входным данным. Некоторые из этих данных могут уже быть в распоряжении разработчика модели, в то время как для сбора других потребуется время и усилия. Обычно значение таких входных данных задаются на основе некоторых гипотез или предварительного анализа. В некоторых случаях точные значения одного (и более) входных параметров оказывают небольшое влияние на результаты прогонов модели. Чувствительность получаемых результатов к изменению входных данных может быть оценена путем проведения серии имитационных прогонов для различных значений входных параметров. Имитационная модель, следовательно, может использоваться для уменьшения затрат времени и средств на уточнение входных данных. После того как разработана модель и собраны начальные входные данные, следующей задачей является перевод модели в форму, доступную для компьютера.
На этапах верификации и валидации осуществляется оценка функционирования имитационной модели. На этапе верификации определяется, соответствует ли запрограммированная для ЭВМ модель замыслу разработчика. Это обычно осуществляется путем ручной проверки вычисления, а также может быть использован и ряд статистических методов.
Установление адекватности имитационной модели исследуемой системы осуществляется на этапе валидации. Валидация модели обычно выполняется на различных уровнях. Специальные методы валидации включают установление адекватности путем использования постоянных значений всех параметров имитационной модели или путем оценивания чувствительности выходов к изменению значений входных данных. В процессе валидации сравнение должно осуществляться на основе анализа как реальных, так и экспериментальных данных о функционировании системы.
Условия проведения машинных прогонов модели определяется на этапах стратегического и тактического планирования. Задача стратегического планирования заключается в разработке эффективного плана эксперимента, в результате которого выясняется взаимосвязь между управляемыми переменными, либо находится комбинация значений управляемых переменных, минимизация или максимизация имитационной модели. В тактическом планировании в отличии от стратегического решается вопрос о том, как в рамках плана эксперимента провести каждый имитационный прогон, чтобы получить наибольшее количество информации из выходных данных. Важное место в тактическом планировании занимают определение условий имитационных прогонов и методы снижения дисперсии среднего значения отклика модели.
Следующие этапы в процессе имитационного исследования- проведение машинного эксперимента и анализ результатов- включают прогон имитационной модели на ЭВМ и интерпретацию полученных выходных данных. Последним этапом имитационного исследования является реализация полученных решений и документирование имитационной модели и ее использование. Ни одни из имитационных проектов не должен считаться законченным до тех пор, пока их результаты не были использованы в процессе принятия решений. Успех реализации во многом зависит от того, насколько правильно разработчик модели выполнил все предыдущие этапы процессов имитационного исследования. Если разработчик и пользователь работали в тесном контакте и достигли взаимопонимания при разработке модели и ее исследовании, то результат проекта скорее всего будет успешно внедряться. Если же между ними не было тесной взаимосвязи, то, несмотря на элегантность и адекватность имитационного моделирования, сложно будет разработать эффективные рекомендации.
Вышеперечисленные этапы редко выполняются в строго заданной последовательности, начиная с определения проблемы и кончая документированием. В ходе имитационного моделирования могут быть сбои в прогонах модели, ошибочные допущения, от которых в дальнейшем приходится отказываться, переориентировки целей исследования, повторные оценки и перестройки модели. Такой процесс позволяет разработать имитационную модель, которая дает верную оценку альтернатив и облегчает процесс принятия решений.
Глава 2. Распределения и генераторы псевдослучайных чисел
Ниже будут использованы следующие обозначения:
X - случайная величина; f(х) - функция плотности вероятности X; F(х) - функция вероятности X;
а - минимальное значение;
b - максимальное значение;
m – мода;
μ -математическое ожидание М[Х]; σ2 —дисперсия М[(Х-μ)2];
σ -среднеквадратичное отклонение; α-параметр функции плотности вероятности;
β - параметр функции плотности вероятности.
2.1 Виды распределений
2.1.1 Равномерное распределение
Функция плотности вероятности равномерного распределения задает одинаковую вероятность для всех значений, лежащих между минимальным и максимальным значениями переменной. Другими словами, вероятность того, что значение попадает в указанный интервал. пропорциональна длине этого интервала. Применение равномерного распределения часто вызвано полным отсутствием информации о случайной величине, кроме ее предельных значений. Равномерное распределение называют также прямоугольным.
f(t) =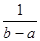 при а ≤ t ≤ Ь. при а ≤ t ≤ Ь.
Среднее значение распределения равно μ = 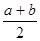 , дисперсия равна σ2
= , дисперсия равна σ2
=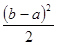 . .
Равномерно распределенная случайная величина X на отрезке [а, b] выражается через равномерно распределенную на отрезке [0, 1] случайную величину Rформулой
X = а + (b - а) *R
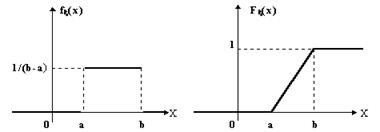
Рис.1 Графики функции распределения и плотности распределения:
2.1.2 Треугольное распределение
Треугольное распределение является более информативным, чем равномерное. Для этого распределения определяются три величины - минимум, максимум и мода. График функции плотности состоит из двух отрезков прямых, одна из которых возрастает при изменении X от минимального значения до моды, а другая убывает при изменении X от значения моды до максимума. Значение математического ожидания треугольного распределения равно одной трети суммы минимума, моды и максимума. Треугольное распределение используется тогда, когда известно наиболее вероятное значение на некотором интервале и предполагается кусочно-линейный характер функции плотности. Функция плотности вероятности треугольного распределения имеет вид:
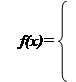 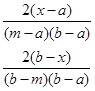 μ=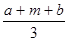 , σ2
= , σ2
=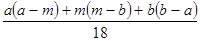 . .
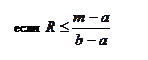
Треугольно распределенная случайная Xсвязана со случайной величиной R, распределенной равномерно на [0,1], соотношением:
, если 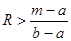 . . |
|
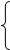 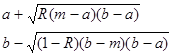 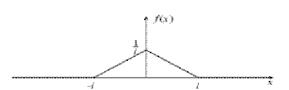
Рис.2 График плотности треугольного распределения
2.1.3 Экспоненциальное (показательное) распределение
Если вероятность того, что один и только один результат наступит на интервале Δt, пропорциональна Δt и если наступление результата не зависит от наступления других результатов, величины интервалов между результатами распределены экспоненциально. Другими словами, работа, продолжительность которой экспоненциально распределена имеет одинаковую вероятность завершения в течение любого последующего периода времени Δt. Таким образом, работа, выполняемая за t единиц времени, имеет ту же вероятность окончания в последующий период Δt, что и только что начатая работа. Подобное отсутствие временной обусловленности называется марковским свойством или свойством отсутствия последействия. Существует прямая связь между предположением об экспоненциальности распределения продолжительности работы и марковским свойством. Экспоненциальное распределение предполагает значительную вариабельность переменной. Если математическое ожидание продолжительности работы равно 1/α, то дисперсия равна 1/α2. По сравнению с большинством остальных распределений экспоненциальное обладает большей дисперсией.
Функция распределения:
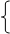
1– e-αt при t≥0, 0 при t<0, 0 при t<0,
α >0 - параметр экспоненциального закона.
С экспоненциальным распределением легко осуществлять математические преобразования, благодаря чему оно применяется в целом ряде исследований.
Методом обратных функций можно показать, что показательно распределенная случайная величина X связана со случайной величиной R, распределенной равномерно на [0,1], соотношением:
Y=-1/α * ln(1-R),
где α - параметр показательного закона.
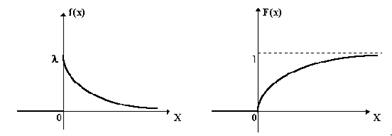
Рис.3 Графики функции распределения и плотности распределения
2.1.4 Распределение Пуассона
Распределение Пуассона является дискретным и обычно связано с числом результатов за определенный период времени. Если продолжительность интервалов между результатами распределена экспоненциально, и в каждый момент времени может произойти только один результат, то можно доказать, что число результатов на фиксированном интервале времени распределено по закону Пуассона. Другими словами, если интервалы между прибытиями распределены экспоненциально, распределение числа прибытий будет пуассоновским.
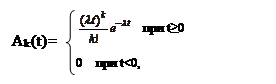
где λ>0, k≥0 - параметры закона. Пуассоновское распределение используется часто как аппроксимация биномиального распределения в том случае, когда оно моделирует последовательности независимых испытаний Бернулли (результаты таких испытаний могут быть типа «да-нет», «стоять-идти», «успех-неудача» и т.п.). При больших значениях математического ожидания пуассоновское распределение аппроксимируется нормальным.
Для получения пуассоновски распределенной случайной величины Y можно воспользоваться следующим методом: установить значение величины Y равным первому значению N, такому, что
где Rn – п-е псевдослучайное число.
2.1.5 Нормальное распределение
Нормальное, или Гауссово, распределение является наиболее важным в теории вероятностей и математической статистике. Эту роль нормальное распределение приобрело в связи с центральной предельной теоремой, которая утверждает, что при весьма нестрогих условиях распределение средней величины или суммы N независимых наблюдений из любого распределения стремиться к нормальному по мере увеличения N. Таким образом, сумму случайных величин часто можно считать нормально распределенной.
Именно благодаря центральной предельной теореме нормальное распределение так часто применяется в исследованиях по теории вероятностей и математической статистике. Существует и другая причина частого применения нормального распределения. Его преимуществом является легкость математического трактования, в связи с чем многие методы доказательств в таких областях, как, например, регрессионный или вариационный анализ, основаны на предположении о нормальном характере функции плотности.
При больших значениях среднего нормальное распределение является хорошей аппроксимацией биноминального распределения.
Функция плотности вероятности нормального закона имеет вид:
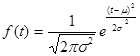
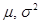 - параметры нормального закона, ( - параметры нормального закона, (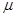 - среднее значение, - среднее значение, 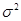 - дисперсия нормального распределения). - дисперсия нормального распределения).
Генератор нормально распределенной случайной величины X можно получить по формулам:
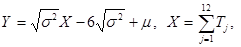
где Tj (j=1,…,12) – значения независимых случайных величин, равномерно распределенных на интервале (0,1).

Рис. 4 График плотности вероятности имеет вид нормальной кривой (Гаусса)
2.2 Виды генераторов случайных чисел
Следует помнить, что генерация произвольного случайного числа состоит из двух этапов:
· генерация нормализованного случайного числа (то есть равномерно распределенного от 0 до 1);
· преобразование нормализованных случайных чисел ri в случайные числа xi, которые распределены по необходимому пользователю (произвольному) закону распределения или в необходимом интервале.
Генераторы случайных чисел (ГСЧ) по способу получения чисел делятся на:
- физические;
- табличные;
- алгоритмические.
2.2.1 Физические ГСЧ
Примером физических ГСЧ могут служить: монета («орел» — 1, «решка» — 0); игральные кости; поделенный на секторы с цифрами барабан со стрелкой; аппаратурный генератор шума (ГШ), в качестве которого используют шумящее тепловое устройство, например, транзистор (рис.1).
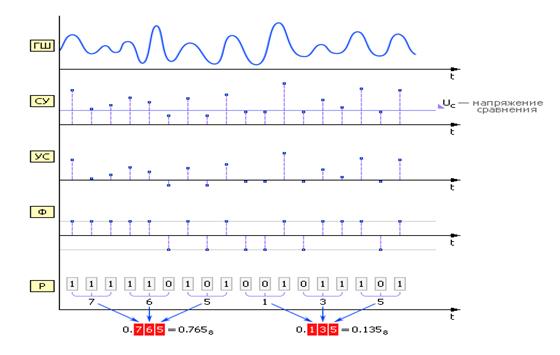
Рис.5 Диаграмма получения случайных чисел аппаратным методом
2.2.2
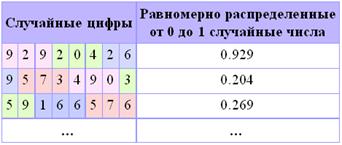
Табличные ГСЧ
Табличные ГСЧ в качестве источника случайных чисел используют специальным образом составленные таблицы, содержащие проверенные некоррелированные, то есть никак не зависящие друг от друга, цифры. В таблице 1 приведен небольшой фрагмент такой таблицы. Обходя таблицу слева направо сверху вниз, можно получать равномерно распределенные от 0 до 1 случайные числа с нужным числом знаков после запятой (в нашем примере мы используем для каждого числа по три знака). Так как цифры в таблице не зависят друг от друга, то таблицу можно обходить разными способами, например, сверху вниз, или справа налево, или, скажем, можно выбирать цифры, находящиеся на четных позициях.
Таблица 1
. Случайные цифры
.
2.2.3
Алгоритмические ГСЧ
Числа, генерируемые с помощью этих ГСЧ, всегда являются псевдослучайными (или квазислучайными), то есть каждое последующее сгенерированное число зависит от предыдущего: 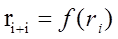
Различают следующие алгоритмические методы получения ГСЧ:
- метод серединных квадратов;
- метод серединных произведений;
- метод перемешивания;
- линейный конгруэнтный метод.
Метод серединных квадратов.
Имеется некоторое четырехзначное число R0. Это число возводится в квадрат и заносится в R1. Далее из R1 берется середина (четыре средних цифры) — новое случайное число — и записывается в R0. Затем процедура повторяется (см. рис. 2).Отметим, что на самом деле в качестве случайного числа берется число с приписанным слева нулём и десятичной точкой.
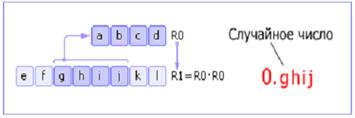
Рис.6 Схема метода средних квадратов
Этот способ был предложен Джоном фон Нейманом и относится к 1946 году.
Метод серединных произведений.
Число R0 умножается на R1, из полученного результата R2 извлекается середина R2* (это очередное случайное число) и умножается на R1. По этой схеме вычисляются все последующие случайные числа (см. рис. 3).
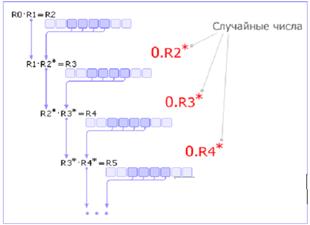
Рис.7 Схема метода серединных произведений
Линейный конгруэнтный метод.
Линейный конгруэнтный метод является одной из простейших и наиболее употребительных в настоящее время процедур, имитирующих случайные числа. В этом методе используется операция mod(x, y), возвращающая остаток от деления первого аргумента на второй. Каждое последующее случайное число рассчитывается на основе предыдущего случайного числа по следующей формуле:
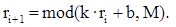
M — модуль (0 < M);
k — множитель (0 ≤ k < M);
b — приращение (0 ≤ b < M);
r0 — начальное значение (0 ≤ r0 < M).
Последовательность случайных чисел, полученных с помощью данной формулы, называется линейной конгруэнтной последовательностью. Многие авторы называют линейную конгруэнтную последовательность при b = 0 мультипликативным конгруэнтным методом, а при b ≠ 0 — смешанным конгруэнтным методом.
Глава 3. Практическая часть
3.1.
Постановка задачи
На станцию технического обслуживания (СТО) согласно закону Эрланга второго порядка со средним временем прибытия 14 мин прибывают автомобили для технического обслуживания (36% автомобили) и ремонта (64% автомобилей).
На СТО есть два бокса для технического обслуживания и три бокса для ремонта. Выполнение простого, средней сложности и сложного ремонтов - равновероятно.
Время и стоимость выполнения работ по техническому обслуживанию и ремонту зависит от категории выполняемых работ (табл. 2).
После технического обслуживания 12% автомобилей поступают для выполнения ремонта средней сложности.
Построить гистограмму времени обслуживания автомобилей.
Оценить
выручку СТО за пять дней работы.
Таблица 2.
| Категория работ
|
Время ремонта, мин
|
Стоимость ремонта, руб
|
| Техническое обслуживание |
Равномерно распределено в интервале 10-55 |
Равномерно распределено в интервале 100-400 |
| Простой ремонт |
Равномерно распределено в интервале 12-45 |
Равномерно распределено в интервале 50-450 |
| Ремонт средней сложности |
Нормально распределено со средним 45 и среднеквадр-ым отклонением 5 |
Равномерно распределено в интервале 100-1400 |
| Сложный ремонт |
Равномерно распределено в интервале 80-150 |
Равномерно распределено в интервале 350-2550 |
Упрощенная схема объекта моделирования:
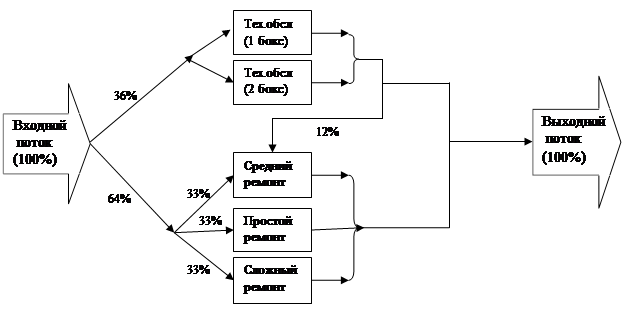
Рис.8 Схема моделирования работы станции технического обслуживания
3.2. Описание метода решения
3.2.1 Описание метода решения задачи вручную
Трудность решения задачи ручным методом состоит в огромном количестве расчетов, которые необходимо произвести. Учитывая это, мы моделируем работу СТО не в течение 5 дней, как указано это в условии задания, а берем небольшой промежуток времени.
В курсовой работе при разработке модели работы СТО применены следующие виды распределения: равномерное и экспоненциальное.
Определим время прибытия автомобилей на СТО, которое имеет экспоненциальное распределение, и рассчитывается по следующей формуле:
u = - ln (
g i
) * λ , λ=1/14
маш
./
мин
(1)
где g
i
–
это случайные числа.
С помощью алгоритмической генерации случайных чисел, используя метод средних квадратов, сгенерировали 30 случайных чисел, которые представлены в таблице 2.
Подставляя полученные случайные числа в формулу (1) получим интервалы времени между поступлениями общего потока автомобилей на СТО, и занесем данные в таблицу 3.
Таблица 3.
| №
|
Случайные числа,
g
i
|
Время поступления требований,
|
Блоки, на которые поступают машины
|
| 1
|
0,0850 |
34,51 |
Тех.обслуживание |
| 2
|
0,2369 |
20,16 |
Тех.обслуживание |
| 3
|
0,3412 |
15,05 |
Тех.обслуживание |
| 4
|
0,9304 |
1,01 |
Слож. ремонт |
| 5
|
0,9716 |
0,40 |
Слож. ремонт |
| 6
|
0,1184 |
29,87 |
Тех.обслуживание |
| 7
|
0,2838 |
17,63 |
Тех.обслуживание |
| 8
|
0,2065 |
22,08 |
Тех.обслуживание |
| 9
|
0,0139 |
59,86 |
Тех.обслуживание + сред. ремонт |
| 10
|
0,6523 |
5,98 |
Средний ремонт |
| 11
|
0,4056 |
12,63 |
Простой ремонт |
| 12
|
0,6892 |
5,21 |
Средний ремонт |
| 13
|
0,8028 |
3,08 |
Слож. ремонт |
| 14
|
0,1368 |
27,85 |
Тех.обслуживание |
| 15
|
0,3270 |
15,65 |
Тех.обслуживание |
| 16
|
0,6431 |
6,18 |
Средний ремонт |
| 17
|
0,6446 |
6,15 |
Средний ремонт |
| 18
|
0,8252 |
2,69 |
Слож. ремонт |
| 19
|
0,2025 |
22,36 |
Тех.обслуживание |
| 20
|
0,6429 |
6,18 |
Средний ремонт |
| 21
|
0,9519 |
0,69 |
Слож. ремонт |
| 22
|
0,1202 |
29,66 |
Тех.обслуживание |
| 23
|
0,9800 |
0,28 |
Слож. ремонт |
| 24
|
0,1061 |
31,41 |
Тех.обслуживание |
| 25
|
0,1841 |
23,69 |
Тех.обслуживание |
| 26
|
0,6490 |
6,05 |
Средний ремонт |
| 27
|
0,0809 |
35,20 |
Тех.обслуживание |
| 28
|
0,2589 |
18,92 |
Тех.обслуживание |
| 29
|
0,9340 |
0,96 |
Слож. ремонт |
| 30
|
0,4139 |
12,35 |
Простой ремонт |
Согласно условию задачи 36% автомобилей поступают на техническое обслуживание, а остальные 64% - на ремонт. Сравниваем доли процентов со случайными числами и, таким образом, определяем, какой именно автомобиль куда поступает:
· если g< 0.36, то на тех. обслуживание;
· если g> 0.36, то на ремонт.
Итого, из потока, поступающих на заправочную станцию 30 автомобилей, 15 автомобилей поступают на тех. обслуживание и 15 - на ремонт.
Далее, умножаем случайные числа, которые меньше 0,36 на 2,78. Это мы делаем для того, чтобы получить 100% из тех 36% машин, которые приехали на тех. обслуживание. Это поможет найти те самые 12% машин, которые после тех. обслуживания поступают на выполнение ремонта средней сложности. Полученные числа сравниваем – если число меньше или равно 0,12, то она после тех.обслуживания поступает и на средний ремонт. После произведенных вычислений мы определили, что 7ая машина, поступившая на тех. обслуживание, поступила также и на ремонт средней сложности.
Далее используем тот же метод для определения того, какие машины, поступившие на ремонт, поступили на простой, средний и сложный ремонты. Умножаем случайные числа, которые больше 0,36 на 1,56. Получившиеся числа сравниваем:
· если число < 0,33 – простой ремонт;
· если число находится в промежутке от 0,33 до 0,66 – средний ремонт;
· если число > 0,66 – сложный ремонт.
Далее определяем время на обслуживание автомобилей.
- Время на тех. обслуживание равномерно распределено в интервале 10-55:
Xтоi = gi(55 - 10) + 10
Стоимость тех.обслуживания также равномерно распределена в интервале 100-400:
Xтоi = gi(400 - 100) + 100
Таблица 4.
| №
|
Случайные числа,
g
i
|
Время обслуживания, мин
|
Случайные числа,
g
i
|
Стоимость обслуживания, руб
|
| 1
|
0,3051 |
23,7295 |
0,663788 |
299,1364 |
| 2
|
0,4534 |
30,403 |
0,131907 |
139,5721 |
| 3
|
0,6705 |
40,1725 |
0,413686 |
224,1058 |
| 4
|
0,8613 |
48,7585 |
0,807198 |
342,1594 |
| 5
|
0,8378 |
47,701 |
0,950983 |
385,2949 |
| 6
|
0,1666 |
17,497 |
0,527365 |
258,2095 |
| 7
|
0,1816 |
18,172 |
0,735827 |
320,7481 |
| 8
|
0,0582 |
12,619 |
0,05409 |
116,227 |
| 9
|
0,0319 |
11,4355 |
0,022308 |
106,6924 |
| 10
|
0,382 |
27,19 |
0,105635 |
131,6905 |
| 11
|
0,5775 |
35,9875 |
0,817392 |
345,2176 |
| 12
|
0,5199 |
33,3955 |
0,599275 |
279,7825 |
| 13
|
0,8518 |
48,331 |
0,281503 |
184,4509 |
| 14
|
0,999 |
54,955 |
0,703246 |
310,9738 |
| 15
|
0,6651 |
39,9295 |
0,158009 |
147,4027 |
Для определения общей стоимости тех. обслуживания сложим все отдельные стоимости:
299,14 + 139,57 + 224,1 + 342,16 + 385,29 + 258,2 + 320,75 + 116,23 + 106,69 + 131,69 + 345,22 + 279,78 + 184,45 + 310,97 + 147,4 = 3591,664
- Время на простой ремонт равномерно распределено в интервале 12-45:
Xпрi = gi(45 - 12) + 12
Стоимость простого ремонта также равномерно распределена в интервале 50-450:
Xпрi = gi(450 - 50) + 50
Таблица 5.
| №
|
Случайные числа,
g
i
|
Время ремонта, мин.
|
Случайные числа,
g
i
|
Стоимость ремонта, руб.
|
| 1
|
0,65671 |
33,67143 |
0,576774 |
280,7096 |
| 2
|
0,529158 |
29,46221 |
0,423461 |
219,3844 |
| 500,094
|
- Время на средний ремонт имеет экспоненциальное распределение со средним 45 и среднеквадратическим отклонением 5:
Xслi = 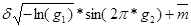
Стоимость среднего ремонта также равномерно распределена в интервале 100-1400:
Xслi = gi(1400 - 100) + 100
Таблица 6.
| №
|
Случайные числа,
g 1
i
|
Случайные числа,
g 2
i
|
Время ремонта, мин.
|
Случайные числа,
g
i
|
Стоимость ремонта, руб.
|
| 1
|
0,65671 |
0,970213 |
43,34725 |
0,481822 |
726,3686 |
| 2
|
0,529158 |
0,620039 |
48,74525 |
0,034647 |
145,0411 |
| 3
|
0,460358 |
0,349485 |
49,32399 |
0,75438 |
1080,694 |
| 4
|
0,445785 |
0,761956 |
41,91791 |
0,194049 |
352,2637 |
| 5
|
0,840672 |
0,978321 |
44,21576 |
0,852098 |
1207,727 |
| 6
|
0,423906 |
0,688784 |
46,04819 |
0,778864 |
1112,523 |
| 7
|
0,763808 |
0,273752 |
46,6651 |
0,653691 |
949,7983 |
| 5574,416
|
- Время на сложный ремонт равномерно распределено в интервале 80-150:
Xпрi = gi(150 - 80) + 80
Стоимость сложного ремонта также равномерно распределена в интервале 350-2550:
Xпрi = gi(2550 - 350) + 350
Таблица 7.
| №
|
Случайные числа,
g
i
|
Время ремонта, мин.
|
Случайные числа,
g
i
|
Стоимость ремонта, руб.
|
| 1
|
0,471298 |
112,9909 |
0,831532 |
2179,37 |
| 2
|
0,548324 |
118,3827 |
0,631296 |
1738,851 |
| 3
|
0,752037 |
132,6426 |
0,82604 |
2167,288 |
| 4
|
0,270129 |
98,90903 |
0,910576 |
2353,267 |
| 5
|
0,37024 |
105,9168 |
0,231733 |
859,8126 |
| 6
|
0,914679 |
144,0275 |
0,351011 |
1122,224 |
| 7
|
0,058792 |
84,11544 |
0,274889 |
954,7558 |
| 11375,57
|
Нужно определить среднее время обслуживания автомобилей на СТО. Для этого сначала определяем среднее время обслуживания для ТО, простого, среднего и сложного ремонтов в отдельности.
- Среднее время тех. обслуживания = общее время тех. обслуживания / число обслуживающихся машин. = 480 / 15 = 32 мин.
- Среднее время простого ремонта = общее время простого ремонта / число обслуживающихся машин. = (50+43) / 2 = 46,5 мин.
- Среднее время среднего ремонта = общее время среднего ремонта / число обслуживающихся машин. = 466 / 7 = 66,57 мин.
- Среднее время сложного ремонта = общее время сложного ремонта / число обслуживающихся машин. = (64+27+27+66+37) / 7 = 31,57 мин.
- Общая стоимость обслуживания на СТО = 3591,664 + 500,094 + 5574,416 + 11375,57 =
21041,74 руб.
Итого среднее время обслуживания автомобилей = (32+46,5+66,57+31,57) / 4 = 44,16 мин.
Для более детального моделирования работы заправочной станции, изобразим нашу СМО в виде графика (график прилагается к работе в виде Приложения).
Интервал времени обслуживания всех машин на графике составляет 546 мин. Имеется 5 обслуживающих блоков: 2 блока для ТО, и по 1 блоку на простой, средний и сложный ремонты.
В каналы поступает один тип заявок – неприоритетные, т.е. поступающие заявки упорядочиваются в очереди и поступают на обслуживание в порядке поступления (первый пришел – первый обслужен).
Канал может обслуживать одновременно только одну заявку. Обслуживание заявок производится в таком порядке: сначала в очереди нет ни одной машины, и колонка свободна. В момент поступления машины начинается его обслуживание. Если следующая машина приезжает в тот момент, когда канал занят, то она становится в очередь. Далее дисциплина обслуживания такова: обслуживается машина, стоящая первая в очереди.
(См. Приложение).
По полученному графику определяем следующие характеристики работы СМО:
- Среднее время задержки (автомобилей): 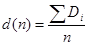
Тех. обслуживание: (11+38+26) /3 = 25
Простой ремонт: нет задержки
Средний ремонт: 265 / 6 = 44,2
Сложный ремонт: 42 / 2 =21
- Средняя длина очереди (автомобилей):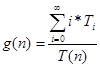 , ,
Где: T
(
n
)
– конечное время работы системы;
T
0
,
T
1
,
T
2
… - промежуток времени, в течении которого в системе находилось соответственно 0, 1, 2 и более требований.
Тех. обслуживание: T
(
n
)
=546; T
0
=471; T
1
=75; g
(
n
)
= 75 / 546 = 0,14
Простой ремонт: нет очереди
Средний ремонт:T
(
n
)
=515; T
0
=249; T
1
=128, T
2
=108, T
3
=29; g
(
n
)
= (128+108*2+29*3) / 515 = 0,84
Сложный ремонт: T
(
n
)
=493; T
0
=451; T
1
=42; g
(
n
)
= 42 / 491 = 0,09
- Максимальная длина очереди (автомобилей): L
(
max
)
= 3 машины
- Коэффициент использования устройства (блоков на СТО):
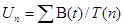 ; ; 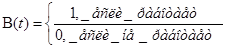 ; ;
Тех. обслуживание: Un = 480 / 546 = 0,88 => 88% - работает, 12% - простой;
Простой ремонт: Un = 92/ 517 = 0,18 => 18% - работает, 72% - простой;
Средний ремонт: Un = 316 / 546 = 0,61 => 61% - работает, 39% - простой;
Сложный ремонт: Un = 221 / 546 = 0,45 => 45% - работает, 55% - простой.
3.3 Блок – схема

3.4 Перевод модели на язык программирования
3.4.1 Выбор
языка программирования
Структурное программирование – это технология создания программ, позволяющая путем соблюдения определенных правил уменьшить время разработки и количество ошибок, а также облегчить возможность модификации программы.
Разные типы процессоров имеют разный набор команд. Если язык программирования ориентирован на конкретный тип процессора и учитывает его особенности, то он называется языком программирования низкого уровня. Языком самого низкого уровня является язык ассемблера, который просто представляет каждую команду машинного кода в виде специальных символьных обозначений, которые называются мнемониками. С помощью языков низкого уровня создаются очень эффективные и компактные программы, так разработчик получает доступ ко всем возможностям процессора. Т .к. наборы инструкций для разных моделей процессоров тоже разные, то каждой модели процессора соответствует свой язык ассемблера, и написанная на нем программа может быть использована только в этой среде. Подобные языки применяют для написания небольших системных приложений, драйверов устройств и т. п.
С помощью языка программирования создается текст, описывающий ранее составленный алгоритм. Чтобы получить работающую программу, надо этот текст перевести в последовательность команд процессора, что выполняется при помощи специальных программ, которые называются трансляторами. Трансляторы бывают двух видов: компиляторы и интерпретаторы. Компилятор транслирует текст исходного модуля в машинный код, который называется объектным модулем за один непрерывный процесс. При этом сначала он просматривает исходный текст программы в поисках синтаксических ошибок. Интерпретатор выполняет исходный модуль программы в режиме оператор за оператором, по ходу работы, переводя каждый оператор на машинный язык.
Языки программирования высокого уровня не учитывают особенности конкретных компьютерных архитектур, поэтому создаваемые программы на уровне исходных текстов легко переносятся на другие платформы, если для них созданы соответствующие трансляторы.
Си – был создан в 70- е годы первоначально не рассматривался как массовый язык программирования. Он планировался для замены ассемблера, чтобы иметь возможность создавать такие же эффективные и короткие программы, но не зависеть от конкретного процессора. Он во многом похож на Паскаль и имеет дополнительные возможности для работы с памятью.
Си++ - объектно-ориентированное расширение языка Си, созданное Бьярном Страуструпом в 1980г.
3.4.2 Программа
Принятые сокращения:
tk –
количество минут (в нашей программе tk = 7200, т.е. 5 дней);
kol
–
количество машин, прибывших на СТО за 5 дней;
st
–
счетчик машин, поступивших на СТО за 5 дней;
i
–
переменная;
j
–
кол-во машин, поступивших на тех. обслуживание;
r
1 -
кол-во машин, поступивших на простой ремонт;
r
2-
кол-во машин, поступивших на средний ремонт;
r
3-
кол-во машин, поступивших на сложный ремонт;
k
,
l
,
m
,
n
–
переменные;
p
–
случайное число;
s
_
to
–
выручка на блоке тех. обслуживания за 5 дней;
s
_
pr
–
выручка по простому ремонту за 5 дней;
s
_
sr
–
выручка по среднему ремонту за 5 дней;
s
_
sl
–
выручка по сложному ремонту за 5 дней;
SUM
–
общая выручка на СТО за 5 дней.
Программный
код
:
#include<iostream.h>
#include<math.h>
#include<stdio.h>
#include<conio.h>
#include<stdlib.h>
void main()
{
int tk,kol,i=0,j=0,r1=0,r2=0,r3=0,k=1,l=1,m=1,n=1;
float p, st=0, s_to=0, s_pr=0, s_sr=0, s_sl=0, SUM;
cin>>tk;
while (st<=tk)
{
p = - log(rand()))/32767*14;
st=st+p;
i++;
}
kol=i;
for (i=1; i<=kol; i++)
{
p=float(rand())/32767;
if (p<=0,12) {j++; r2++;}
else if (p>0,12 && p<=0,36) j++;
else if (p>0,36 && p<=0,57) r1++;
else if (p>0,57 && p<=0,78) r2++;
else r3++;
}
while (k<=j)
{
p= float(rand())/32767*300+100;
s_to=s_to+p;
k++;
}
while (l<=r1)
{
p=float(rand())/32767*400+50;
s_pr=s_pr+p;
l++;
}
while (m<=r2)
{
p=float(rand())/32767*1300+100;
s_to=s_to+p;
k++;
}
while (n<=r3)
{
p=float(rand())/32767*2200+350;
s_sl=s_sl+p;
n++;
}
SUM=s_to+s_pr+s_sr+s_sl;
cout<<"viruchka za 5 dnei ravna"<<SUM<<endl;
}
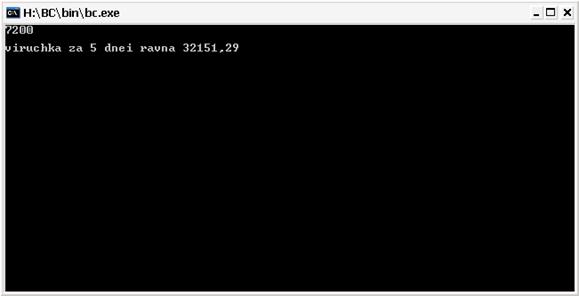
Рис.9 Результат выполнения программы
Заключение
Широкое внедрение электронно-вычислительной техники во все сферы нашей жизни в последнее время, вызвало бурный рост технологий, связанных с применением в них средств вычислительной техники. Одной из наиболее крупных отраслей развития технологий с применением ЭВМ, является математическое моделирование, которое достаточно просто (в отличие от аналогового моделирования) может быть реализовано на ЭВМ разных модификаций и возможностей. Связано это с тем, что при математическом моделировании модель представляет собой определенную последовательность математических зависимостей и динамика такой модели представляет собой изменение параметров зависимостей в результате выполнения расчетов. Математическое моделирование тесно связано с имитационным моделированием. Одним из разделов математического моделирования, являются модели систем массового обслуживания и их изучение.
В данном курсовом проекте была построена имитационная модель СТО с использованием программы С++, при этом мы использовали программу моделирования процесса с N обрабатывающими устройствами и с очередью. В результате моделирования мы вычислили: выручку на СТО за 5 дней, построили график обслуживания автомобилей, программу и блок-схему.
Список использованной литературы
1. Емельянов А.А. «имитационное моделирование экономических процессов» 2002г
2. Советов В.Я., Яковлев С.А. «Моделирование системы» 2001г.
3. Соболь И.М. «Метод Монте-Карло» 1968г.
4. Шеннон Р. «Имитационное моделирование систем – искусства и науки» 1978г.
5. «Машинные имитационные эксперименты с моделями экономических систем» под редакцией Нейлера.
6. Бусленко М.П. «Моделирование сложных систем».
7. Кеольтон В., Лод А. «Имитационное моделирование. Классика CS» издание 3-е, 2004г.
|