СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. Геометрический метод решения задач ЛП
2. Симплекс-метод
2.1 Идея симплекс-метода
2.2 Реализация симплекс-метода на примере
2.3 Табличная реализация простого симплекс-метода
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
ВВЕДЕНИЕ
Тема моей работы касается решения задач, возникающих в экономике. При этом встает вопрос о выборе наилучшего в некотором смысле варианта решения. А на поиск возможного варианта часто влияют разного рода факторы, сужающие рамки выбора. Иначе говоря, требуется решить задачу оптимизации, которая состоит в необходимости выбора наилучшего варианта решений среди некоторого, как правило, ограниченного множества возможных вариантов.
Задача оптимизации может быть сформулирована на языке математики, если множество доступных вариантов удается описать с помощью математических соотношений (равенств, неравенств, уравнений), а каждое решение - оценить количественно с помощью некоторого показателя, называемого критерием оптимальности или целевой функцией. Тогда наилучшим решением будет то, которое доставляет целевой функции наибольшее или наименьшее значение, в зависимости от содержательного смысла задачи. Так, например, при инвестировании ограниченной суммы средств в несколько проектов естественной является задача выбора тех проектов, которые могут принести в будущем наибольшую прибыль. При доставке в магазины продукции от различных поставщиков возникает задача минимизации транспортных затрат.
Процесс формализации задачи называется построением ее математической модели. Он состоит из трех этапов.
1. Выбор параметров задачи, от которых зависит решение. Эти параметры называют управляющими переменными и обозначают 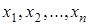 , формируя из них вектор , формируя из них вектор 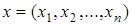 . Принять решение – это значит задать конкретные значения переменных. . Принять решение – это значит задать конкретные значения переменных.
2. Построение числового критерия, по которому можно сравнивать различные варианты решений. Такой критерий принято называть целевой функцией и обозначать через 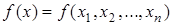 . .
3. Описание всего множества X
допустимых значений переменных – ограничений, связанных с наличием материальных ресурсов, финансовых средств, технологическими возможностями и т.п..
Математическая задача оптимизации состоит в нахождении такого допустимого решения 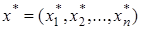 , которое доставляет целевой функции наибольшее или наименьшее значение среди всех возможных решений. , которое доставляет целевой функции наибольшее или наименьшее значение среди всех возможных решений.
Реклама

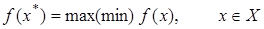 . .
Этот метод часто используется при решении задач, в которых только две неизвестных величины. Разберем его на следующих примерах:
Пример 1.1
. (Задача о производстве красок).
Небольшая фабрика изготовляет два вида красок: INT
- для внутренних работ и EXT
- для наружных работ. В производстве красок используются два исходных продукта А
и В
. Из-за малой площади склада максимально возможные суточные запасы этих продуктов равны 6 т. и 8 т. соответственно. На производство 1 тонны краски INT
расходуется 1 тонна продукта А
и 2тонны продукта В
, а на изготовление 1 тонны краски EXT
идет 2 тонны продукта А
и 1 тонна продукта В
. Фабрика продает краску по цене 3тыс. долл. за тонну краски INT
и 2 тыс. долл. за тонну краски EXT
. Исходные данные удобно свести в таблицу:
| Исходные продукты |
Расход продукта на 1
т. краски |
Запас продуктов |
| INT |
EXT |
| A
|
1 |
2 |
6 |
| B
|
2 |
1 |
8 |
| Цена 1
т. краски |
3 тыс. долл. |
2 тыс. долл. |
Изучение рынка сбыта показало, что суточный спрос на краску EXT
никогда не превышает спрос на краску INT
, более чем на 1 тонну. Какое количество краски каждого вида должна производить фабрика в сутки, чтобы доход от реализации продукции был максимален?
Построим математическую модель задачи. Для этого надо определить переменные задачи, целевую функцию и ограничения, которым удовлетворяют переменные. Обозначим через x1
- планируемый суточный объем производства краски INT, а через x2
- суточный объем производства краски EXT. Целевая функция f(x)
будет выражать суточный доход от продажи краски, равный 3x1
+ 2x2
(тыс. долл.). Этот доход подлежит максимизации
f(
x)= 3
x1
+ 2
x2
®
max.
Построим ограничения задачи, связанные с ограниченными запасами продуктов А
и В
. На производство краски INT
в количестве x1
(т) будет использовано 1x1
(т) продукта А
, а на производство краски EXT
в объеме x2
(т) будет затрачено 2x2
(т) продукта А
. Поскольку суточный запас продукта А
равен 6 т., то расход продукта А
на изготовление красок двух видов не может превышать в сутки этой величины: 1x1
+ 2x2
£ 6
. Аналогично получим ограничение, связанное с запасом продукта В
: 2x1
+1x2
£ 8
. Ограничение по соотношению спроса на краски можно описать неравенством: x2
- x1
£ 1
. Учитывая естественные условия неотрицательности объемов выпуска продукции, окончательно получим следующую задачу линейного программирования
Реклама

f(x) = 3 x1
+ 2 x2
®
max
(1.1)
1 x1
+ 2 x2
£
6
, (1.2)
2 x1
+ 1 x2
£
8
, (1.3)
- x1
+ x2
£ 1
, (1.4)
x1
³ 0, x2
³ 0
. (1.5)
Построим множество планов задачи, описываемое ограничениями (1.2)-(1.5). Рассмотрим первое неравенство. Оно задает некоторую полуплоскость, расположенную по одну сторону от граничной прямой
p1
: 1x1
+2x2
=6
Построим эту прямую на плоскости с координатными осями x1
и x2
. Для проведения прямой достаточно знать две ее точки. Проще всего найти точки пересечения прямой с осями координат. Полагая x1
= 0
, из уравнения прямой получим x2
= 3
, а при x2
= 0
найдем x1
= 6
. Таким образом прямая p1
пройдет через точки (0,3)
и (6,0)
. Чтобы определить, по какую сторону от прямой расположена искомая полуплоскость, достаточно подставить в неравенство (1.2) координаты любой точки плоскости. Если прямая не проходит через начало координат, то удобнее всего взять точку (0, 0)
. Очевидно, что в этой точке неравенство (1.2) строго выполняется (1* 0 + 2* 0 < 6)
, значит полуплоскость, определяемая этим неравенством, лежит ниже прямой p1
,
включая в себя начало координат. Искомую полуплоскость отметим штриховкой (рис.1.1
).
Аналогично построим полуплоскость, задаваемую неравенством (1.3).
Для этого нанесем на координатную плоскость граничную прямую
p2
: 2x1
+x2
=8
,
найдя ее точки пересечения с осями координат: (0,8)
и (4,0)
.
Подставляя координаты точки (0,0)
в неравенство (2.3), видим, что начало координат лежит в искомой полуплоскости (2* 0 + 1* 0 < 8)
, значит все точки, удовлетворяющие неравенству (2.3), расположены левее прямой p2
. Отметим эту область штриховкой (рис.1.1
).
Точки, задаваемые ограничением (4
), находятся ниже прямой
p3
: -x1
+x2
=1,
проходящей через точки (0, 1)
и (-1, 0)
.
Наконец, условия неотрицательности: x1
³ 0, x2
³0 задают все точки первой четверти, что также отметим штриховкой.
Выделяя теперь точки плоскости, удовлетворяющие всем ограничениям задачи (1.1)-(1.5), то есть расположенные одновременно во всех заштрихованных полуплоскостях, получаем множество планов X
. Оно представляет собой многоугольник (в данной задаче - пятиугольник). Его стороны лежат на прямых, уравнения которых получаются из исходной системы неравенств (1.2)-(1.5) заменой знаков неравенств на строгие равенства.
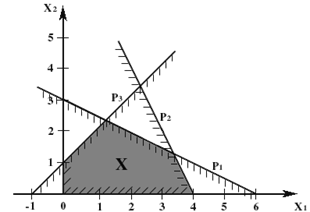
Рис. 1.1
Для графического представления целевой функции введем понятие линии уровня (изолинии функции).
Определение.
Линией уровня (изолинией) функции f(x)
называется множество точек x = (x1,
x2
)
, в которых она принимает одно и то же постоянное значение f(x) = h
, где h
- некоторое число. Для линейной функции двух переменных f(x) = c1
x1
+ c2
x2
линия уровня, соответствующая числу h
, будет представлять прямую с уравнением
c1
x1
+
c2
x2
=
h
(1.6)
При изменении числа h
будем получать семейство линий уровня (параллельных прямых) с одним и тем же направляющим вектором c = =(c1
, c2)
, перпендикулярным всем прямым. Известно, что вектор c = (c1
, c2
)
для линейной функции f(x) = c1
x1
+c2
x2
указывает направление ее возрастания. Геометрически это означает, что при параллельном перемещении прямой (1.6) в направлении целевого вектора c
значение целевой функции возрастает.
Построим линии уровня целевой функции f(x) = 3x1
+ 2 x2
в нашей задаче. Их уравнения будут иметь вид 3x1
+ 2 x2
= h.
Они задают семейство параллельных прямых, зависящих от параметра h
. Все прямые перпендикулярны целевому вектору c = (3, 2)
, составленному из коэффициентов целевой функции, поэтому для построения семейства линий уровня целевой функции достаточно построить ее целевой вектор, и провести несколько прямых, перпендикулярных этому вектору. Линии уровня будем проводить на множестве планов X
, помня при этом, что при параллельном перемещении прямых в направлении целевого вектора c = (3, 2)
значение функции f(x)= 3x1
+ 2x2
будет возрастать. Поскольку в задаче оптимальный план должен доставлять целевой функции максимально возможное значение, то для решения задачи графически надо среди всех точек x = (x1,
x2
)
множества планов X
найти такую точку x* = (x1
*,
x2
*)
, через которую пройдет последняя линия уровня в направлении целевого вектора c = (3,2)
. Из рисунка 1.2 видно, что искомой точкой будет точка, лежащая в вершине множества X
, образованной пересечением прямых p1
и p2
. Решая систему уравнений, описывающих эти прямые найдем оптимальный план
x1
* = 3 1
/3
, x2
* = 1 1
/3
. При этом максимальное значение целевой функции будет равно f(x*) = 12 2
/3
.
Таким образом, ежесуточно фабрика должна производить 3 1
/3
тонн краски INT
и 1 1
/3
тонн краски EXT
, получая при этом доход 12 2
/3
тыс. долларов.
x1
+ 2 x2
= 6,
2 x1
+ x2
= 8,
Пример 1.2.
Лечебное предприятие закупает два вида мультивитаминных комплексов «Здоровье» и «Долголетие» с содержанием витаминов трех видов. Количество единиц этих витаминов в одном грамме мультикомплексов, необходимая их норма при профилактическом приеме и стоимость одного грамма комплексов «Здоровье» и «Долголетие» отражены в таблице
| Витамины |
Кол-во единиц витаминов в 1
гр. комплекса |
Норма единиц витаминов |
| Здоровье |
Долголетие |
| V
1
|
3 |
1 |
9 |
| V
2
|
1 |
2 |
8 |
| V
3
|
1 |
6 |
12 |
| Стоимость 1
грамма комплекса |
5 руб. |
4 руб. |
Сколько граммов мультивитаминных комплексов каждого вида требуется на один профилактический прием, чтобы были получены все витамины не меньше требуемой нормы, и при этом их суммарная стоимость была минимальной.
Составим математическую модель задачи. Для этого введем переменные: x1
– количество комплекса «Здоровье» (гр.)
, x2
– количество комплекса «Долголетие» (гр.)
, необходимое для профилактического приема. Целевая функция выражает суммарную стоимость витаминных комплексов, которая должна быть минимально возможной
f(
x)= 5
x1
+ 4
x2
®
min
(1.7)
Ограничения, описывающие выполнение норм по витаминам, имеют вид:
По витамину V1
: 3x1
+ x2
³9
, (1.8)
По витамину V2
: x1
+ 2x2
³ 8,
(1.9)
По витамину V3
: x1
+ 6x2
³12
. (1.10)
При этом переменные должны быть неотрицательны: xj
³0, j = 1, 2.
Снова начнем решение с построения множества планов X
, для чего проведем граничные прямые, уравнения которых получаются при замене в ограничениях знаков неравенств на равенства
p1
: 3
x1
+
x2
= 9,
p2
: x1
+ 2
x2
= 8,
p3
: x1
+ 6
x2
= 12.
Подставляя координаты точки (0,0)
в неравенства (1.8)-(1.10) видим, что начало координат им не удовлетворяет и, следовательно, не входит в множество планов Х
. Поэтому штриховки направлены выше и правее граничных прямых. Выделяя точки, удовлетворяющие всем неравенствам и условиям неотрицательности, получаем множество планов, изображенное на рис. 1.2. В данном примере оно не ограничено.
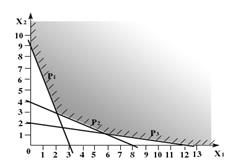
Рис. 1.2
Изобразим целевую функцию (1.7) с помощью линий уровня. Для этого достаточно построить целевой вектор c = (5, 4)
и перпендикулярно ему провести несколько прямых на множестве Х.
Поскольку целевой вектор указывает направление возрастания целевой функции, а в задаче о рационе требуется найти ее минимум, то для нахождения оптимального решения будем перемещать линию уровня параллельно самой себе по множеству Х
в направлении, противоположном целевому вектору.
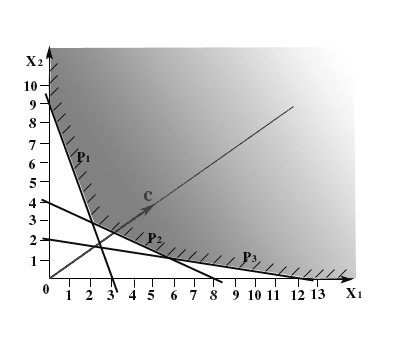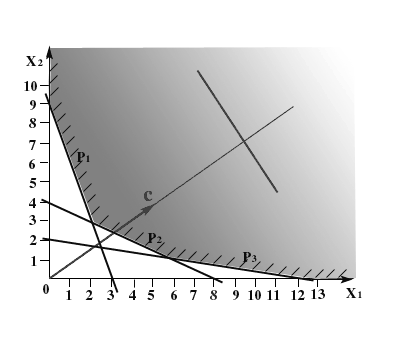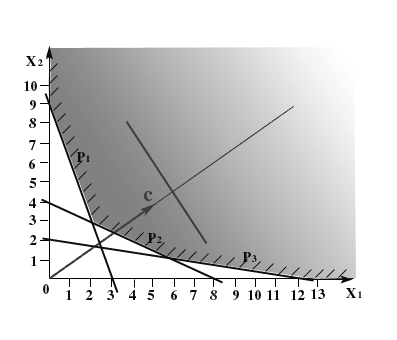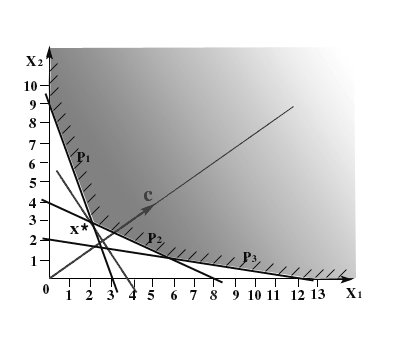 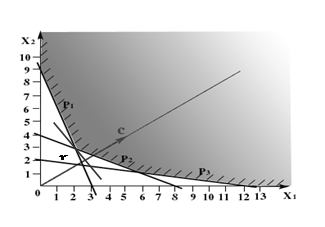
Рис. 1.3
Последней точкой множества планов, через которую еще проходит линия уровня будет точка пересечения прямых p1
и p2
. Решая систему уранений (рис. 1.3).
3 x1
+ x2
= 9
x1
+ 2 x2
= 8
получим оптимальный план x1
* = 2, x2
* = 3.
Минимальное значение целевой функции при этом будет равно
f(x*) = 5∙2 + 4∙3 = 22.
Следовательно, самый дешевый набор для профилактического приема состоит из 2 гр
. комплекса А и 3 гр
. комплекса В
, и его стоимость равна 22
руб.
Теперь несложно сформулировать геометрический способ решения стандартных задач ЛП с двумя переменными:
· изображается допустимый многоугольник 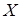 – пересечение полуплоскостей, являющихся решениями соответствующих неравенств; – пересечение полуплоскостей, являющихся решениями соответствующих неравенств;
· изображается целевой вектор 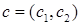 ; ;
· через допустимое множество проводится перпендикуляр к целевому вектору – это линия уровня целевой функции;
· путем перемещения линии уровня параллельно самой себе в направлении целевого вектора до тех пор, пока 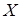 не окажется по одну сторону от перемещаемой прямой, визуально определяется точка (или точки) максимума; не окажется по одну сторону от перемещаемой прямой, визуально определяется точка (или точки) максимума;
· вычисляются координаты точки максимума (решением соответствующей системы уравнений, задающих прямые, точка пересечения которых и есть искомая точка) и максимальное значение целевой функции.
Замечание.
Для определения точки минимума следует перемещать изолинию против направления целевого вектора.
В разобранных примерах оптимальный план находился в единственной вершине многоугольника допустимых планов. Однако при решении задач ЛП могут встретиться и другие случаи.
Бесконечное множество оптимальных планов.
На рис.1.4
целевая функция принимает одно и то же максимальное значение в любой точке отрезка AB
, соединяющего две вершины множества планов Х
. Такая ситуация возникает, если линии уровня параллельны граничной прямой.
Отсутствие ограниченного решения
. На рис.1.5
изображен случай, когда целевая функция не ограничена сверху на множестве планов и решение задачи на максимум не существует. При этом решение задачи на минимум может существовать, (как в задаче о витаминах).
Отсутствие допустимых планов.
На рис.1.6
области, допустимые по каждому из ограничений, не имеют общих точек. В этом случае говорят, что ограничения несовместны, множество планов пусто и задача ЛП решения не имеет.
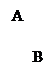  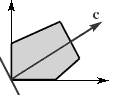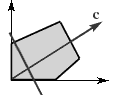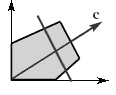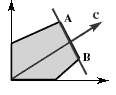 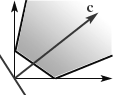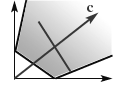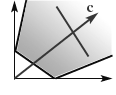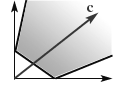 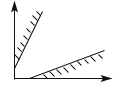
Рис. 1.4 Рис. 1.5 Рис. 1.6
2.1 Идея симплекс-метода
Рассмотрим универсальный метод решения канонической задачи линейного программирования
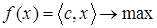 , , 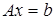 , , 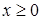 , ,
с n
переменными и m
ограничениями-равенствами, известный как симплекс-метод.
Множество планов канонической задачи – выпуклое многогранное множество, имеющее конечное число угловых точек. И если эта задача имеет оптимальное решение, то оно достигается хотя бы в одной угловой точке.
С любой угловой точкой связан базисный план задачи, в котором 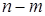 переменных равны нулю, а оставшимся переменным соответствуют линейно независимые столбцы матрицы условий переменных равны нулю, а оставшимся переменным соответствуют линейно независимые столбцы матрицы условий 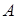 . Эти линейно независимые столбцы образуют невырожденную базисную матрицу . Эти линейно независимые столбцы образуют невырожденную базисную матрицу 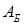 . .
Перебор всех угловых точек сопряжен с большими вычислительными затратами и поэтому не эффективен. В 1947 году Дж. Данциг предложил упорядоченную процедуру перебора угловых точек, при которой для нахождения оптимального решения достаточно исследовать лишь небольшую их часть. Эта процедура называется симплекс-методом
.
Дж. Данциг предложил при переходе от одной крайней точки к другой заменять в базисной матрице всего один вектор. Это означает, что при таком переходе мы должны одну из базисных переменных исключить – сделать ее небазисной (равной нулю), а на ее место ввести новую переменную из числа небазисных (нулевых) – сделать ее базисной (положительной).
Оказывается, геометрически такая замена приводит к переходу от одной угловой точки к смежной (соседней), связанной с предыдущей точкой общим ребром.
Из всех соседних точек выбирается та, в которой целевая функция возрастает более всего. Поскольку число угловых точек конечно, через конечное число переходов будет найдена вершина с наибольшим значением целевой функции, либо будет установлена неограниченность целевой функции на неограниченном множестве планов.
Общая схема симплекс-метода состоит из следующих основных шагов.
· шаг 0
. Определение начального базиса 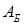 и соответствующей ему начальной угловой точки (базисного плана) и соответствующей ему начальной угловой точки (базисного плана) 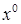 . .
· шаг 1
. Проверка текущего базисного плана на оптимальность.
Если критерий оптимальности выполнен,топлан оптимален и решение закончено. Иначе
переход на шаг 2.
· шаг 2
. Нахождение переменной, вводимой в состав базисных. (Из условия увеличения целевой функции).
· шаг 3
. Нахождение переменной, исключаемой из состава базисных переменных (Из условия сохранения ограничений задачи).
· шаг
4
. Нахождение координат нового базисного плана (смежной угловой точки). Переход на шаг 1.
Повторяющиеся шаги 1–4 образуют одну итерацию симплекс-метода.
Из этой схемы следует, что во-первых, для начала работы симплекс-метода надо иметь какую-то угловую точку – начальный базисный план, а во-вторых, надо уметь исследовать текущую угловую точку на оптимальность, не вычисляя всех смежных вершин. Эти проблемы легко решаются, если каноническая задача ЛП имеет некий специальный вид.
Определение
. Будем говорить, что каноническая задача ЛП имеет "предпочтительный вид", если
1. правые части уравнений 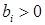 , , 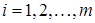 . .
2. матрица условий 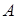 содержит единичную подматрицу размера содержит единичную подматрицу размера 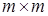
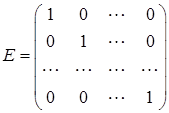 . .
Другими словами, в любом уравнении есть переменная с коэффициентом равным единице, отсутствующая в остальных уравнениях. Первое условие не является обременительным, так как в случае отрицательной правой части некоторого уравнения, достаточно умножить его на (–1). В задаче предпочтительного вида начальный базисный план находится очень просто.
Пример 2.1.
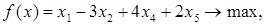
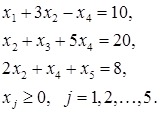
Матрица условий A
и вектор правых частей ограничений b
имеют вид
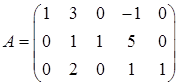 , , 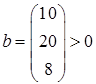 , ,
а целевой вектор с = (1, -3, 0, 4, 2).
Сразу очевидна одна базисная матрица: 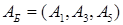 с единичными векторами условий. с единичными векторами условий.
Следовательно, выбирая в качестве базисных переменных x1
, x3
,x5
,
и полагая в системе уравнений x2
=
x4
=
0 (небазисные переменные),
немедленно находим x1
=
10,x3
=
20,x5
=
8, так что начальный базисный план x0
= (10, 0, 20, 0, 8).Видим, что значения базисных переменных равны правым частям ограничений. Из этого понятно требование положительности правых частей bi
.
В дальнейшем, базисные переменные будем объединять в вектор xБ.
Таким образом, в канонической задаче предпочтительного вида в качестве начальной базисной матрицы берется единичная подматрица AБ
= E
, а соответствующие ей базисные переменные равны правым частям ограничений:
xБ
= b
.
Для базисного плана такого вида может быть сформулирован достаточно простой для проверки критерий оптимальности. Введем величины
∆j
= < сБ
, Aj
> – cj
, j = 1,...,n,
(2.1)
где сБ
– вектор из коэффициентов целевой функции при базисных переменных xБ
, Aj
–
j-
йстолбец матрицы условий, cj
–
j-
й коэффициент целевой функции. Разности ∆j
называются симплексными разностями или симплексными оценками.
Критерий оптимальности базисного плана
. Если для базисного плана с единичной базисной матрицей все симплексные оценки неотрицательны, то этот план оптимален.
Применим данный критерий для проверки на оптимальность базисного плана x0
= (10, 0, 20, 0, 8) из примера 2.1.
Так как в этом плане вектор базисных переменных xБ
=(x1
, x3
,x5
), то сБ
= (c1
, c3
,c5
) = (1, 0, 2).
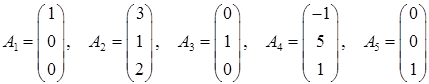 . .
Следовательно,
∆1
= < сБ
, A1
> – c1
=1∙1 + 0∙0 + 2∙0 – 1= 0,
∆2
= < сБ
, A2
> – c2
=1∙3 + 0∙1 + 2∙2 – (-3) = 10,
∆3
= < сБ
, A3
> – c3
=1∙0 + 0∙1 + 2∙0 – 0= 0,
∆4
= < сБ
, A4
> – c4
=1∙(-1) + 0∙5 + 2∙1 – 4= -3,
∆5
= < сБ
, A5
> – c5
=1∙0 + 0∙0 + 2∙1 – 2= 0.
Так как оценка ∆4
< 0, то базисный план x0
не оптимален. Заметим, что симплексные оценки, соответствующие базисным переменным, всегда равны нулю, так что достаточно проверять только небазисные оценки.
2.2 Реализация симплекс-метода на примере
Продемонстрируем применение симплекс-метода на примере. Рассмотрим каноническую задачу ЛП
| f(x)
= x
1
+
2x
2
+
0 x
3
+
0 x
4
→max |
(2.2) |
| –x
1
+
2x
2
+ x
3
=
4, |
(2.3) |
| 3 x
1
+
2x
2
+ x
4
=
12, |
(2.4) |
| xj
≥ 0, j =
1,2,3,4. |
(2.5) |
Матрица условий A
= (A
1
, A
2
, A
3
, A
4
), где
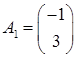 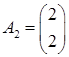 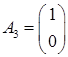 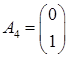
Целевой вектор c
=(c1
,
c2
,
c3
,
c4
) = (1, 2, 0, 0); вектор правых частей b
=(b
1
,
b
2
) = (4, 12).
Шаг 0.
Нахождение начальной угловой точки (базисного плана).
Задача имеет предпочтительный вид, так как правые части уравнений положительны, а столбцы матрицы условий A
3,
A
4
образуют единичную подматрицу. Значит начальная базисная матрица 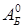 =
(A
3
, A4
);
x
3
иx
4
–
базисные переменные,x
1
иx
2
-
небазисные переменные, cБ
= (c
3,
c
4)
= = (0,
0). =
(A
3
, A4
);
x
3
иx
4
–
базисные переменные,x
1
иx
2
-
небазисные переменные, cБ
= (c
3,
c
4)
= = (0,
0).
Начальный базисный план имеет вид x0
=
(0, 0, x
3
, x
4)
= (0, 0, 4, 12); f(
xo
)= 0.
Шаг 1.
Проверка базисного плана на оптимальность.
Подсчитаем симплексные оценки для небазисных переменных по формуле (5.1)
1
= <
cБ
,
A
1
> –
c
1
=
0 ·(–1) +
0 ·3 – 1 = –1.
2
= <
cБ
,
A
2
> –
c
2
=
0 ·2 + 0 · 2 – 2 = –2.
Так как оценки отрицательны, то план x –
не оптимален. Будем искать новый базисный план (смежную угловую точку) с большим значением целевой функции.
Шаг 2
. Нахождение переменной вводимой в базис.
Целевую функцию можно увеличить, если ввести в состав базисных переменных (сделать положительной) одну из небазисных переменных x
1
илиx
2
, поскольку обе оценки j
< 0. Обычно в состав базисных вводят небазисную переменную с наибольшей по модулю отрицательной оценкой, поэтому будем вводить в базис переменную x
2.
Шаг 3.
Определение переменной выводимой из базиса.
После ввода в базис переменной x2
новый план будет иметь вид
x' =
(0, x
2,
x
3
, x
4
).
Этот план не является базисным, так как он содержит только одну нулевую координату, значит надо сделать нулевой (исключить из базиса) одну из переменных x
3
или x
4
. Подставим координаты плана x' =
(0, x
2,
x
3
, x
4
) в ограничения задачи. Получим
2x
2
+
x
3
=
4,
2x
2
+ x
4
= 12.
Выразим отсюда базисные переменные x
3
и x
4
через переменную x
2
,
вводимую в базис.
| x
3
= 4 – 2x
2,
|
(2.6) |
| x
4
= 12 – 2x
2
. |
(2.7) |
Так переменные x
3
и x
4
должны быть неотрицательны, получим систему неравенств
| 4 – 2x
2
≥0, |
(2.8) |
| 12 – 2x
2
≥ 0. |
(2.9) |
Чем больше значение x
2
,
тем больше возрастает целевая функция. Найдем максимальное значение новой базисной переменной, не нарушающее ограничения задачи, то есть удовлетворяющее условиям (2.8), (2.9).
Перепишем последние неравенства в виде
2x
2
≤ 4,
2x
2
≤ 12,
откуда максимальное значение x
2
= min { 4/2, 12/2 } = 2. Подставляя это значение в выражения (2.6), (2.7) для x
3
и x
4
,получаем x
3
= 0.Следовательно x3
выводится из базиса.
Шаг 4.
Определение координат нового базисного плана.
Новый базисный план (смежная угловая точка) имеет вид
x'
= (0, x
2,
0, x
4
)
Базис этой точки состоит из столбцов A
2
и A
4
,
так что 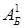 = (A
2,
A
4
). Этот базис не является единичным, так как вектор A
2
= (2,2),и следовательно задача (2.2)–(2.5) не имеет предпочтительного вида относительно нового базиса. Преобразуем условия задачи (2.3), (2.4) таким образом, чтобы она приняла предпочтительный вид относительно новых базисных переменных x
2,
x
4,
то есть чтобы переменная x
2
входила в первое уравнение с коэффициентом, равным единице, и не присутствовала во втором уравнении. Перепишем уравнения задачи = (A
2,
A
4
). Этот базис не является единичным, так как вектор A
2
= (2,2),и следовательно задача (2.2)–(2.5) не имеет предпочтительного вида относительно нового базиса. Преобразуем условия задачи (2.3), (2.4) таким образом, чтобы она приняла предпочтительный вид относительно новых базисных переменных x
2,
x
4,
то есть чтобы переменная x
2
входила в первое уравнение с коэффициентом, равным единице, и не присутствовала во втором уравнении. Перепишем уравнения задачи
– x
1
+ 2 x
2
+ x
3
= 4, (p
1)
3x
1
+2 x
2
+ x
4
= 12. (p
2)
Поделим первое уравнение на коэффициент при x
2
.Получим новое уравнение 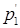 = p
1
/ 2, эквивалентное исходному = p
1
/ 2, эквивалентное исходному
– 1/2 x
1
+ x
2
+ 1/2 x
3
= 2. (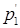 )
)
Используем это уравнение, которое назовем разрешающим, для исключения переменной x
2
из второго уравнения. Для этого надо уравнение 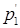 умножить на 2 и вычесть из p
2
.
Получим
умножить на 2 и вычесть из p
2
.
Получим 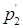 = p
2
–
2 = p
2
–
2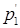 = p
2
– p
1
: = p
2
– p
1
:
4 x
1
– x
3
+ x
4
= 8. (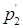 )
)
В итоге получили новое "предпочтительное" представление исходной задачи относительно новых базисных переменных x
2
, x
4
:
f
(x
) = x
1
+ 2 x
2
+ 0 x
3
+ 0 x
4
max
– 1/2 x
1
+ x2
+ 1/2 x
3
= 2 (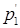 )
)
4 x
1
– x
3
+ x
4
= 8 (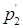 )
)
xj
0, j
=
1,2,3,4
Подставляя сюда представление нового базисного плана x
1
=
(0, x
2,
0, x
4
), сразу найдем его координаты, так как значения базисных переменных равны правым частям уравнений
x'
= (0, 2, 0, 8); f
(x
1
)=4.
На этом завершается первая итерация простого симплекс-метода. Далее процесс решения задачи продолжается с шага 1, состоящем в проверке найденного плана на оптимальность. Решение заканчивается тогда, когда все симплексные оценки текущего базисного плана окажутся неотрицательными.
Мы не будем проводить вторую итерацию по схеме первой, поскольку все вычисления симплекс-метода удобнее проводить в табличном виде.
2.3 Табличная реализация простого симплекс-метода
Табличную реализацию продемонстрируем на том же примере (2.2)–(2.5).
Шаг 0
. Решение начинается с построения начальной симплекс-таблицы. Сначала заполняется правая часть таблицы с третьей колонки. В двух верхних строках записываются имена переменных задачи (x
1,
...,x
4
) и коэффициенты целевой функции при этих переменных. Ниже записываются коэффициенты уравнений – элементы матрицы условий А
, так что под переменной x
1
располагаетсястолбец A
1
, под переменной x
2
–
столбец A
2
и т.д. В правый столбец заносятся правые части ограничений (числа bi
> 0).
Затем находим столбцы матрицы условий, образующие единичный базис – в нашем примере это A
3
и A
4
и соответствующие им базисные переменные x
3,
x
4
записываем во вторую колонку. Наконец, в первом столбце записываем коэффициенты целевой функции при базисных переменных.
Таблица 1 - Начальная симплекс-таблица
| СБ
|
Базисные переменные |
с1
=1
|
с2
=2
|
с3
=0
|
с4
=0
|
Значения базисных перем. (x
Б
=
b
) |
| x1
|
x2
|
x3
|
x 4
|
| c3
=0
|
x3
|
a11
=-1
|
a12
=2
|
a13
=1
|
a14
=0
|
b1
=4
|
| c4
=0
|
x4
|
a21
=3
|
a22
=2
|
a23
=0
|
a24
=1
|
b2
=12
|
| Строка оценок j
|
1
= -1
|
2
= -2
|
3
= 0
|
4
= 0
|
f(x)= 0
|
Так как задача имеет предпочтительный вид, то значения базисных переменных равны правым частям уравнений, расположенным в последнем столбце. Поскольку небазисные переменные равны нулю, то начальный базисный план равен
x
o
= (0, 0, x
3
, x
4)
= (0, 0, 4, 12).
Шаг 1.
Для проверки плана x
o
на оптимальность подсчитаем симплексные оценки для небазисных переменных x
1
и x
2
по формуле
j
=< cБ
, Aj
> – cj
.
1
= < cБ
, A
1
> – c
1
=
0 ·(–1) +
0 ·3 – 1 = –1.
При табличной реализации для подсчета оценки 1
надо найти сумму произведений элементов первого столбца (cБ)
на соответствующие элементы столбца A
1
при небазисной переменной x
1
. Аналогично подсчитывается оценка 2
,
как скалярное произведение первого столбца (cБ)
на столбец при переменной x2
.
2
= <
cБ
,
A
2
> –
c
2
=
0 ·2 + 0 · 2 – 2 = –2.
Симплексные оценки записываются в последней строке симплекс-таблицы, которая называется дельта-строкой. При этом заполняются не только клетки при небазисных переменных, но и базисные клетки. Легко проверить, что для базисных единичных столбцов матрицы условий симплексные оценки равны нулю. В последней клетке строки оценок записываем значение целевой функции в точке xo
.
Заметим, что, так как небазисные координаты базисного плана равны нулю, то подсчет целевой функции удобно производить по формуле
f
(x
)= < cБ
, xБ
>,
перемножая скалярно первый и последний столбцы таблицы.
Так как среди оценок j
естьотрицательные,
то план x
o
– не оптимальный, и надо найти новый базисный план, заменив одну из базисных переменных на новую из числа небазисных.
Шаг 2.
Поскольку обе оценки
1
и
2
< 0,то в базис можно включить любую из переменных x
1,
x2
. Введем в базис переменную с наибольшей по модулю отрицательной оценкой, то есть x
2
.
Столбец симплекс-таблицы, в котором находится вводимая в базис переменная называется ведущим столбцом
.
В примере ведущим будет столбец при x2
.
Шаг 3.
Если в ведущем столбце все элементы отрицательны, то решения задачи не существует и max f
(x
) . В примере все элементы ведущего столбца положительны, следовательно, можно найти максимальное значение x
2
,
при котором одна из старых базисных переменных обратится в ноль. Напомним, что максимальное значение x2
=
min{4/2, 12/2}=2.
По таблице это значение вычисляется как наименьшее из отношений компонент базисного плана (из последнего столбца) к соответствующим положительным
элементам ведущего столбца.
Наименьшее отношение находится в строке с базисной переменной x3.
Значит переменная x3
исключается из состава базисных переменных (x
3
= 0).
Строка, содержащая переменную, исключаемую из базиса, называется ведущей строкой.
В примере ведущей строкой будет первая строка.
Элемент, находящийся на пересечение ведущей строки и ведущего столбца, называется ведущим элементом.
В нашем случае ведущий элемент a
12
= 2.
Табл. 2 - Начальная симплекс-таблица с ведущими строкой и столбцом
| cБ
|
Базисные перемен. |
с1
=1
|
с2
=2
|
с3
=0
|
С4
=0
|
Значения базисных перем. |
Уравнения |
| x1
|
x2
|
x3
|
x 4
|
| c3
=0
|
x
3
|
–1
|
2
|
1
|
0
|
4
|
p1
|
| c4
=0
|
x4
|
3
|
2
|
0
|
1
|
12
|
p2
|
| Строка оценок j
|
1
= –1
|
2
= –2
|
3
= 0
|
4
= 0
|
f(x)= 0
|
Шаг 4
. Для получения нового базисного плана приведем задачу к новому предпочтительному виду относительно новых базисных переменных.
Для этого построим новую симплекс-таблицу, во втором столбце которой вместо исключаемой переменной x3
запишем новую базисную переменную x2
, а в первом столбце (сБ
) вместо с3
запишем коэффициент целевой функции при x2
: c2
=2
. В новой симплекс таблице столбец при x2
долженстать единичным (ведущий элемент должен равняться единице, а все остальные элементы должны обратиться в ноль). Это достигается следующими преобразованиями строк таблицы.
a. Все элементы ведущей строки делим на ведущий элемент и записываем в той же строке новой симплекс- таблицы.
Полученную строку p1
'
назовем разрешающей.
b. К оставшейся второй строке прибавим разрешающую строку, умноженную на такое число, чтобы элемент, стоящий в ведущем столбце обратился в ноль.
p2
'= p2
+ (- 2) p1
'= p2
- p1.
c. Заполним последнюю строку, вычислив оценки j
' = < cБ
', Aj
' > - - cj
,где cБ
', Aj
' -
соответствующие столбцы новой симплекс-таблицы, и значение целевой функции f(x)= < cБ
', xБ
' >.
Получим вторую симплекс-таблицу с новым базисом.
Таблица 3 - Результат первой итерации
| cБ
'
|
Базисные перемен. |
с1
=1
|
с2
=2
|
с3
=0
|
с4
=0
|
Значения базисных перем. |
Уравнения |
| x1
|
x2
|
x3
|
x 4
|
| c2
=2
|
x
2
|
–1/2
|
1
|
1/2
|
0
|
2
|
p1
' =p1
/2 |
| c4
=0
|
x4
|
4
|
0
|
-1
|
1
|
8
|
p2
' =p2
- p1
|
| оценки j
'
|
–2
|
0
|
1
|
0
|
f(x')=4
|
Новый базисный план x
' =
(0, x2
,
0, x4)
= (0, 2, 0, 8
).
Поскольку оценка 1
= -2 < 0,
то план x
'
не оптимален. Для перехода к новому базисному плану (соседней угловой точки) проведем еще одну итерацию симплекс - метода.
Так как
1
< 0,
то в базис вводится переменная x1
.
Первый столбец, содержащий x1
-
ведущий.
Находим отношения компонент базисного плана к соответствующим положительным
элементам ведущего столбца и в качестве ведущей строки берем строку с наименьшим отношением. В таблице 2 в ведущем столбце только второй элемент больше нуля (= 4), следовательно, вторая строка будет ведущей
, а расположенная в ней базисная переменная x4
подлежит исключению из базиса
.
Выделяем ведущий столбец и ведущую строку и на их пересечении находим ведущий элемент (= 4)
.
Строим новую (третью) симплекс-таблицу, заменяя в ней базисную переменную x4
на x1
,
и снова преобразуя строки таблицы таким образом, чтобы ведущий элемент стал равным единице, а остальные элементы ведущего столбца обратились в ноль. Для этого ведущую (вторую) строку делим на 4, а к первой строке прибавляем полученную вторую строку, деленную на 2. Последнюю строку вычисляем по формулам для симплексных оценок j
'' = < cБ
'', Aj
'' > - cj
,где cБ
'', Aj
'' -
соответствующие столбцы новой симплекс-таблицы. Значение целевой функции на новом базисном плане находим по формуле f(x
'')= < cБ
'', xБ
'' >.
Таблица 4 - Результат второй итерации
| cБ
''
|
Базисн. перемен. |
с1
=1
|
с2
=2
|
с3
=0
|
с4
=0
|
Значения базисных перем. |
уравнения |
| x1
|
x2
|
x3
|
x 4
|
| c2
=2
|
x2
|
0
|
1
|
3/8
|
1/8
|
3
|
p1
''=
p1
'+p2
''/2 |
| c1
=1
|
x1
|
1
|
0
|
-1/4
|
1/4
|
2
|
p2
'' = p2
'/4 |
| оценки j
''
|
0
|
0
|
1/2
|
1/2
|
f(x
'')= 8
|
Новый базисный план x
'' =
(x1
, x2
,
0, 0)
= (2, 3, 0, 0
).
Поскольку все оценки неотрицательны, то план x
'' - оптимальный план.
Таким образом, x*
= (2, 3, 0, 0
), f(x*) = 8.
Рассмотренные способы решения задач линейного программирования широко используются на практике. Однако следует отметить, что математическая модель всегда беднее реальной экономической системы. Она описывает эту систему лишь приблизительно, выделяя одни свойства и пренебрегая другими. Для компенсации указанного недостатка в математической экономике разрабатывается несколько типов моделей, каждый из которых призван отразить какую-то одну определённую сторону экономической действительности с тем, чтобы при решении конкретной экономической задачи можно было подобрать такую модель, которая лучше всего к ней подходит.
1. Ашманов С.А. Линейное программирование. – М.: Наука, 1981.
2. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. – М.: Высшая школа, 1980.
3. Калихман И.Л. Линейная алгебра и программирование. – М.: Высшая школа, 1967.
4. Нит И.В. Линейное программирование. – М.: Изд-во МГУ, 1978.
5. Юдин Д.Б., Гольштейн Е.Г. Линейное программирование. Теория и конечные методы. – М.: Физматиз, 1963.
6. Тарасенко Н.В. Математика-2. Линейное программирование: курс лекций. – Иркутск: изд-во БГУЭП, 2003.
7. Математическое программирование в примерах и задачах: Учеб. пособие. – 2-е изд., испр. и доп. – М.: Высш. шк., 1993. – 336 с.
8. www.yandex.ru
9. www.mathematica.ru
10. www.monax.ru
|