Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Санкт-Петербургский государственный политехнический университет»
Факультет экономики и менеджмента
Кафедра «Предпринимательство и коммерция»
ЛАБОРАТОРНАЯ РАБОТА №1
По дисциплине «Статистика»
На тему «Анализ эмпирического распределения»
Санкт-Петербург 2008
Введение
Ряд распределения – это распределение единиц совокупности по значению того или иного признака. Комплексный анализ ряда распределения включает:
- Табличное и графическое представление ряда распределения;
- Расчёт и анализ показателей центра и структуры распределения;
- Расчёт и анализ показателей вариации;
- Характеристику формы распределения;
- Выбор теоретического распределения, которому соответствует изучаемое эмпирическое [1].
Ряды распределения могут быть:
1) Вариационными;
2) Атрибутивными.
Одна из важнейших целей изучения рядов распределения состоит в том, чтобы выявить закономерность распределения и определить ее характер. Закономерности распределения наиболее отчетливо проявляются только при большом количестве наблюдений (т.н. закон больших чисел).
Исходными данными для анализа служит информация, полученная из сборника Росстата Регионы России [2], а именно статистическая информация о числе собственных легковых автомобилей на 1000 человек населения в различных регионах России в 1990 году. Объём исходной совокупности – 87 единиц.
Анализ распределений направлен на выявление закономерности изменения частот в зависимости от значений варьирующего признака и анализ различных характеристик изучаемого распределения. Прежде, чем приступить к вычислению специальных статистических показателей, необходимо из исходной совокупности исключить единицы, не подчиняющиеся общей закономерности распределения, так называемые выбросы. Выбросы – это значения признака, резко отличающиеся как в большую, так и в меньшую сторону, от значений признака основной части единиц совокупности [3].
Для локализации и устранения выбросов необходимо, прежде всего, ранжировать исходные данные. Затем, в ППП Statistica строится график Boxplot на основании ранжированной совокупности. Единицы совокупности, обозначенные на графике звёздочками (*), являются выбросами, которые необходимо исключить из изучаемой совокупности.
Реклама

Вариационным называется ряд распределения, построенный по количественному признаку. Он может быть представлен в виде таблицы и графически. Табличное представление позволяет не только выявить ту или иную закономерность распределения, но и подробно охарактеризовать структуру изучаемой совокупности.
Таблицы вариационных рядов строятся по принципам группировки. Известные проблемы возникают при определении числа групп, поскольку формула Стерджеса (1.1), рекомендуемая для этих целей, дает приемлемые результаты только в условиях больших статистических совокупностей. Процесс определения числа выделяемых групп, в значительной степени, носит творческий характер и требует от исследователя применения не только теоретических знаний, но и практического опыта и интуиции.
Формула Стерджеса:
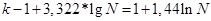 , (1.1) , (1.1)
где k– число групп; N –
объем совокупности.
Использование ППП значительно упрощает задачу табличного представления вариационного ряда, поскольку позволяет с малыми временными затратами просмотреть несколько таблиц с разным числом групп и размером группировочного интервала. Конечный вариант таблицы должен отвечать следующим требованиям: в таблице не должно быть малонаполненных и нулевых групп; нужно стремиться к получению мономодального распределения (т.е. по обе стороны от максимальной частоты должно наблюдаться закономерное убывание частот). Если не удается избавиться от многовершинности в распределении, это, как правило, означает, что изучаемая статистическая совокупность неоднородна и требует более детального изучения. В этих условиях следует либо работать с выбросами, либо, если единицы совокупности не подчиняются единой закономерности распределения, разбить совокупность на объективно существующие группы, и анализировать их раздельно [3].
Далее представлены таблицы вариационного ряда, построенные с использованием разного числа интервалов.
Таблица 1.1. Распределение регионов России по числу собственных легковых автомобилей на 1000 человек населения в 1990 году. k=8
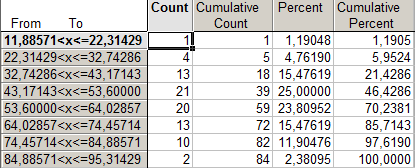
Таблица 1.2. Распределение регионов России по числу собственных легковых автомобилей на 1000 человек населения в 1990 году. k=6
При k=8 получено много малонаполненных групп, что является нежелательным для анализа ряда распределения. Выбирая окончательный вариант табличного представления вариационного ряда в работе, следует остановиться на группировке с использованием 6 групп. Тогда величина группировочного интервала составит 14,6.
Реклама

Необходимо подвести предварительные итоги (на примере третьей строки): только в тридцати регионах России, что составляет 35,71% от общего числа регионов, количество автомобилей на 1000 человек населения в 1990 году составляло от 46,3 до 60,9 штук. В пятидесяти пяти регионах России (65,47% от всех регионов) количество автомобилей на 1000 человек населения в 1990 году составляло менее 60,9 штук.
Табличное представление вариационного ряда позволяет получить подробную информацию о составе и структуре изучаемой совокупности, т.е. определить какое количество единиц изучаемой совокупности обладает тем или иным значением признака и какова доля этой группы единиц в общем объеме совокупности, а также выявить закономерность изменения частот.
На основе таблиц строятся графики, наглядно представляющие закономерность распределения анализируемой статистической совокупности. Графическое представление может быть осуществлено как использованием абсолютных, так и относительных частот [3].
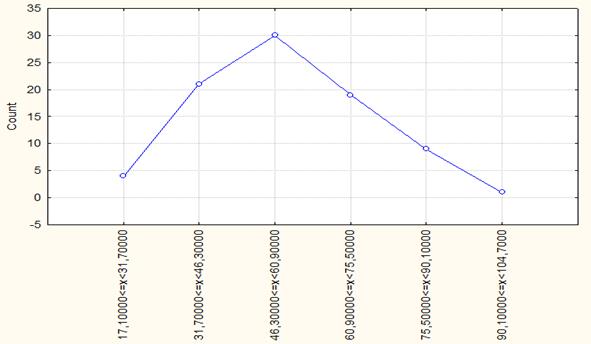
Рис. 1.1. Полигон распределения регионов России по числу собственных легковых автомобилей на 1000 человек населения в 1990 году
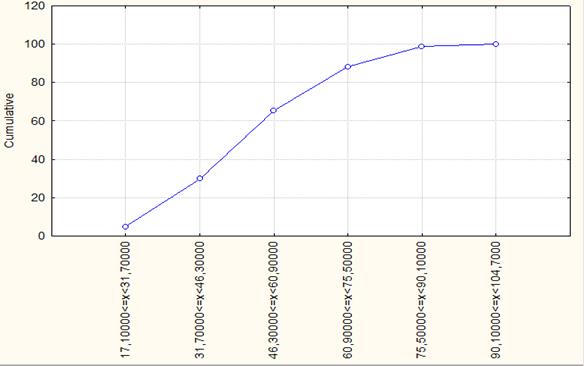
Рис. 1.2. Кумулята распределения регионов России по числу собственных легковых автомобилей на 1000 человек населения в 1990 году
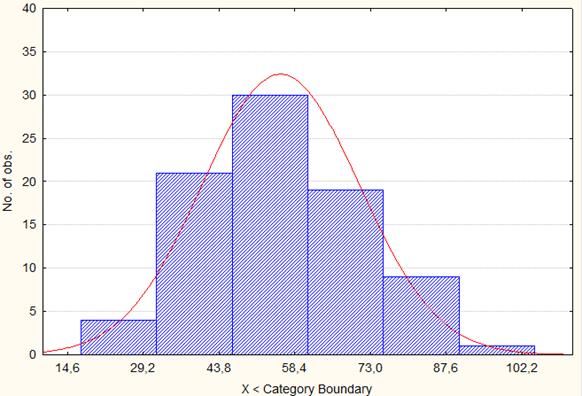
Рис. 1.3 Гистограмма распределения регионов России по числу собственных легковых автомобилей на 1000 человек населения в 1990 году
Среднее значение признаков совокупности, мода и медиана характеризуют центральную тенденцию распределения, указывают тот уровень признака, который является типичным, характерным для данной совокупности. Использование того или иного показателя распределения зависит от типа исходных данных и цели исследования. Поскольку средняя величина рассчитывается на единицу совокупности, но с использованием всех индивидуальных значений признака, она является обобщённой характеристикой всей совокупности [1].
Формулы расчёта.
Средняя арифметическая простая:
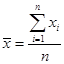 , ,
где 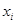 – значение признака у i‑ой единицы совокупности, n – объём совокупности. – значение признака у i‑ой единицы совокупности, n – объём совокупности.
Медиана:
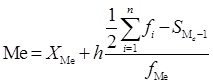 , ,
где 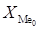 – нижняя граница медианного интервала, – нижняя граница медианного интервала, 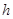 – величина группировочного интервала, – величина группировочного интервала, 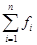 – сумма частот ( – сумма частот (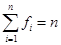 ), ), 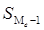 – накопленная частота интервала, предшествующего медианному; – накопленная частота интервала, предшествующего медианному; 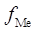 – частота медианного интервала. – частота медианного интервала.
Мода:
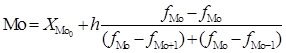 , ,
где 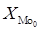 - нижняя граница модального интервала, - нижняя граница модального интервала, 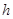 - величина группировочного интервала, - величина группировочного интервала, 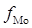 – частота модального интервала, – частота модального интервала,
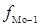 / / 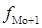 – частота интервала, предшествующего / следующего за модальным. – частота интервала, предшествующего / следующего за модальным.
Таблица 2.1. Показатели центра и структуры распределения
| Показатель центра |
Значение |
| Среднее значение |
55,70595 |
| Медиана |
56,15000 |
| Мода |
52,87000 |
В среднем в регионах России количество автомобилей на 1000 человек населения в 1990 году составляло 55,71 штуку. В 50% регионов России количество автомобилей на 1000 человек населения в 1990 году было меньше 56,15 штук, а в другой половине – больше.
Вариация – различия у индивидуального значения признака изучаемой совокупности. Расчёт показателей центра сопровождается расчётом показателей вариации. Показатели вариации бывают:
- Абсолютные (размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение);
- Относительные (коэффициент осцилляции, относительное линейное отклонение, коэффициент вариации) [1].
Формулы расчёта.
Размах вариации:
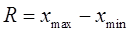 , ,
где 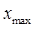 и и 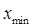 – максимальное и минимальное значение признака совокупности. – максимальное и минимальное значение признака совокупности.
Дисперсия:
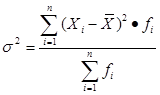 , ,
где 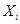 – значение признака у i‑ой единицы совокупности, – значение признака у i‑ой единицы совокупности, 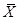 – средняя арифметическая, – средняя арифметическая, 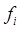 – частота у i‑ой единицы совокупности, – частота у i‑ой единицы совокупности, 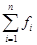 – сумма частот ( – сумма частот (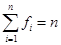 ). ).
Среднее квадратическое (стандартное) отклонение:
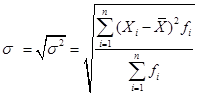 . .
Коэффициент вариации:
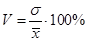
Таблица 3.1. Показатели вариации
| Показатель вариации |
Значение |
| Размах вариации R |
73 |
| Дисперсия s2
|
227,8647 |
| Среднее квадратическое отклонениеs |
15,0952 |
| Коэффициент вариации V |
27,0980% |
Размах вариации, разность между максимальным и минимальным значениями совокупности, составляет 73 единицы. Дисперсия содержательно не интерпретируется, однако является важнейшим показателем вариации, на основе которого рассчитывается ряд статистических показателей, в том числе и коэффициент вариации, в данном случае равный 27,0980%. Коэффициент вариации оценивает степень количественной однородности изучаемой совокупности. В данном случае совокупность можно признать однородной, т.к. коэффициент вариации меньше 33%.
В 1990 году в регионах России число автомобилей на 1000 человек населения отличалось от среднего по стране на 15,0952 штук.
К показателям структуры, кроме медианы, также относят квартили, которые делят совокупность на четыре части, децили (10 частей) и прочие показатели. Использование тех или иных характеристик зависит от цели исследования и от объёма изучаемой совокупности (с увеличением объёма растёт число групп). В данной работе необходимо подсчитать только медиану и квартили [1].
Формулы расчёта.
Нижний квартиль:
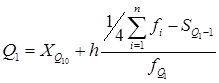 . .
Верхний квартиль:
 . .
Таблица 4.1. Показатели структуры
| Показатель структуры |
Значение |
| Нижний квартиль |
44,80 |
| Медиана |
56,15 |
| Верхний квартиль |
65,80 |
В 50% регионов России количество автомобилей на 1000 человек населения в 1990 году составляло от 44,80 до 65,80 штук.
Форма распределения имеет следующие характеристики:
- Асимметрия;
- Эксцесс (куртозис).
Соответственно существуют коэффициенты асимметрии и эксцесса и стандартные ошибки для этих коэффициентов. Коэффициент асимметрии оценивает, насколько распределение симметрично относительно центра. Коэффициент эксцесса оценивает крутизну распределения, т.е. степень выпада вершины распределения относительно кривой нормального распределения. Эксцесс имеет смысл оценивать только тогда, когда в эмпирическом распределении присутствует несущественная асимметрия.
Формулы расчёта.
Коэффициент асимметрии:
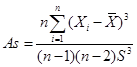 . .
Стандартная ошибка:
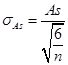 . .
Коэффициент эксцесса:
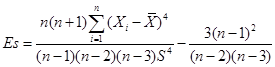 . .
Стандартная ошибка:
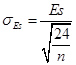 . .
Таблица 5.1. Показатели формы
| Показатель формы |
Значение |
| Коэффициент асимметрии As |
0,032687 |
| Стандартная ошибка sAs
|
0,262651 |
| Коэффициент эксцесса Es |
-0,377168 |
| Стандартная ошибкаsEs
|
0,519660 |
По результатам подсчётов делаются следующие выводы: распределение имеет очень незначительную правостороннюю асимметрию, кроме того есть незначительный отрицательный эксцесс, это значит, что в совокупности не сформировалось «ядро» распределения.
Процедура выравнивания, сглаживания анализируемого распределения заключается в замене эмпирических частот теоретическими, определяемыми по формуле теоретического распределения, но с учетом фактических значений переменной. На основе сопоставления эмпирических и теоретических частот рассчитываются критерии согласия, которые используются для проверки гипотезы о соответствии исследуемого распределения тому или иному типу теоретических распределении.
Выбор конкретного типа модельного распределения осуществляется исходя из самых общих соображений, опирающихся на визуальный анализ построенных графиков распределения. В практическом анализе обязательной является проверка соответствия изучаемого распределения нормальному закону распределения. Необходимость этого связана с тем, что условием применения значительного числа статистических характеристик и оценок является наличие нормального распределения.
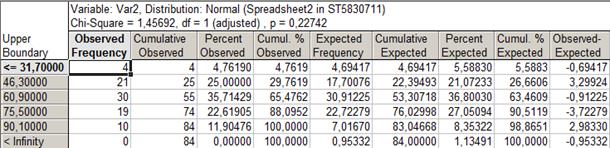
Проверка гипотезы о нормальном распределении регионов России по числу автомобилей на душу населения в 1990 году основывается на расчёте критерия
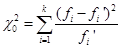 , ,
где 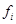 – эмпирические абсолютные частоты, – эмпирические абсолютные частоты, 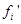 – абсолютные частоты теоретического распределения, k – число интервалов. – абсолютные частоты теоретического распределения, k – число интервалов.
Таблица 6.1. Проверка гипотезы о нормальном распределении регионов России по числу автомобилей на душу населения в 1990 году
Формулы, по которым рассчитывается плотность модельного распределения, а также формулы для расчета теоретических частот распределения могут быть легко найдены в общедоступной справочной и учебной литературе. В данной лабораторной работе используются формулы для нормального распределения.
Функция нормального распределения: 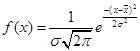 , плотность нормального распределения: , плотность нормального распределения:
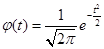 , ,
где 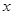 – значение изучаемого признака, – значение изучаемого признака, 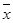 - средняя арифметическая величина, - средняя арифметическая величина, 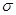 - среднее квадратическое отклонение изучаемого признака, e, π – математические константы, - среднее квадратическое отклонение изучаемого признака, e, π – математические константы, 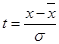 – нормированное отклонение. – нормированное отклонение.
Теоретические частоты нормального отклонения рассчитываются по следующей формуле:
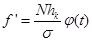 , ,
где N – объём совокупности, hk
– величина интервала. В моём случае вариационный ряд построен с использованием равных интервалов, следовательно: 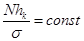 . .
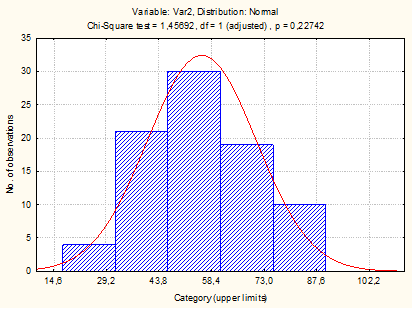
Рис. 6.1. Гистограмма и расчётная кривая распределения регионов России по числу собственных легковых автомобилей на 1000 человек населения в 1990 г.
В шапке таблицы находятся следующие показатели: 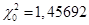 , , 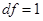 (уточнённое значение числа степеней свободы, (уточнённое значение числа степеней свободы,
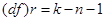 , ,
где k – число интервалов вариационного ряда, n – число параметров теоретического распределения, определяемых по опытным данным, для нормального закона n=2, p – расчётный уровень значимости).
Принятие решения о справедливости гипотезы о законе распределения можно осуществить, ориентируясь на эмпирическое значение критерия 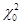 , который сравнивается с табличным значением , который сравнивается с табличным значением 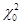 . Окончательные выводы по проверке гипотезы о законе распределения: так как . Окончательные выводы по проверке гипотезы о законе распределения: так как 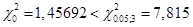 , то гипотеза о нормальном распределении регионов России по числу собственных легковых автомобилей на 1000 человек населения в 1990 г. не противоречит истине. , то гипотеза о нормальном распределении регионов России по числу собственных легковых автомобилей на 1000 человек населения в 1990 г. не противоречит истине.
Только в тридцати регионах России, что составляет 35,71% от общего числа регионов, количество автомобилей на 1000 человек населения в 1990 году составляло от 46,3 до 60,9 штук. В пятидесяти пяти регионах России (65,47% от всех регионов) количество автомобилей на 1000 человек населения в 1990 году составляло менее 60,9 штук.
В среднем в регионах России количество автомобилей на 1000 человек населения в 1990 году составляло 55,71 штуку. В 50% регионов России количество автомобилей на 1000 человек населения в 1990 году было меньше 56,15 штук, а в другой половине – больше.
Размах вариации, разность между максимальным и минимальным значениями совокупности, составляет 73 единицы. В 1990 году в регионах России число автомобилей на 1000 человек населения отличалось от среднего по стране на 15,0952 штук. Коэффициент вариации оценивает степень количественной однородности изучаемой совокупности. В данном случае совокупность можно признать однородной, т. к. коэффициент вариации меньше 33% (V=27,098%).
В 50% регионов России количество автомобилей на 1000 человек населения в 1990 году составляло от 44,80 до 65,80 штук.
Распределение имеет очень незначительную правостороннюю асимметрию, кроме того есть незначительный отрицательный эксцесс, это значит, что в совокупности не сформировалось «ядро» распределения.
Данное распределение соответствует нормальному закону распределения по критерию Пирсона.
1. Лекции по дисциплине статистика. Лектор – доц. О.А. Пономарёва, 2008.
2. Сборник Росстата Регионы России. Социально-экономические показатели. 2006.
3. Учебное пособие. Статистика. Методы анализа распределений. Выборочное наблюдение. Н.В. Куприенко, О.А. Пономарёва, Д.В. Тихонов. 132 с. – 2008.
|