Міністерство освіти і науки України
Національний університет водного господарства та природокористування
Кафедра електротехніки і автоматики
Курсова робота
"Аналіз типової системи автоматичного регулювання температури в печі"
з курсу:
"Теорія автоматичного управління лінійними системами"
Виконав:
Студент III курсу
ФПМіКІС
групи АУТП-31
Реут Д.Т.
Керівник:
ас. Кінчур О.Ф.
Рівне-2009
Зміст
1. Принцип дії cистеми
2. Поведінка системи при зміні задаючої і збурюючої величин
3. Визначення передаточних функцій елементів системи
4. Структурна схема, передаточні функції і рівняння динаміки та статики системи
5. Аналіз стійкості системи та визначення критичного значення коефіцієнта передачі регулятора
6. Побудова годографа амплітудно-фазової частотної характеристики розімкнутої системи і визначення запасу стійкості
7. Розрахувати та побудувати перехідну характеристику системи автоматичного регулювання за каналом задаючої дії при нульових початкових умовах
8. Моделювання перехідних процесів за допомогою комп’ютерної програми SIAM
9. Оцінка якості регулювання
10. Шляхом моделювання процесів на ЕОМ побудувати перехідну характеристику системи за каналом збурюючої дії
11. Зробити висновок про статичні та динамічні властивості досліджуваної системи і, при необхідності, провести її коригування
Висновок
Список використаної літератури
Клапан регулює подачу палива в об’єкт регулювання залежно від положення. Зміна положення проводиться двигуном через редуктор. Отже, вхідною величною є переміщення клапана, а вихідною - витрата палива.
Об’єкт регулювання представляє собою піч, у якій подане паливо спалюється й утворюється пропорційна масі палива кількість теплоти, що спричиняє підвищення температури в печі. Отримана теплота розсіюється у навколишнє середовище та йде на зміну структури та/або агрегатного стану речовин у печі. Усталений режим об’єкта регулювання характеризується рівністю кількості тепла, що утворюється в печі внаслідок згоряння палива, і розсіюваної у навколишнє середовище. Вхідною величиною є витрата палива, а вихідною - температура в печі.
Електричний міст, одним з опорів якого є металевий терморезистор (термометр опору), який змінює свій опір залежно від температури Rt
=R0
(1+αt). За допомогою зміни опору R1
задають бажану температуру в печі. Якщо температура в печі (вхідна величина) рівна заданій 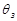 , то опори терморезистора і потенціометра-задавача рівні, міст збалансований (напруга на вимірювальній діагоналі моста рівна нулю). Зміна температури призводить до зміни опору терморезистора, а отже розбалансу моста і появі напруги на вимірювальній діагоналі , то опори терморезистора і потенціометра-задавача рівні, міст збалансований (напруга на вимірювальній діагоналі моста рівна нулю). Зміна температури призводить до зміни опору терморезистора, а отже розбалансу моста і появі напруги на вимірювальній діагоналі 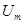 - вихідної величини, полярність якої залежить від знаку різниці (Rt
-R1
), який визначає напрямок переміщення клапана. - вихідної величини, полярність якої залежить від знаку різниці (Rt
-R1
), який визначає напрямок переміщення клапана.
Реклама

Підсилювач збільшує вхідну величину (напругу на діагоналі моста 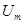 ) в kп
разів, формуючи вихідний сигнал ) в kп
разів, формуючи вихідний сигнал 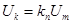 . .
Напруга Uk,
що подається на якір двигуна постійного струму з незалежним збудженням Uзб
, приводить в обертання вал, з’єднаний через редуктор, який зменшує кутову швидкість та збільшує обертовий момент, з клапаном. Залежно від полярності напруги Uk
вал двигуна переміщуватиме клапан в одну чи іншу сторону, збільшуючи або зменшуючи подачу палива. Таким чином вхідною величною системи "двигун-редуктор" є напруга з виходу підсилювача 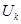 , а вихідною - переміщення клапана. , а вихідною - переміщення клапана.
Зміна задаючої величини R1
призводить до появи напруги 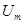 , яка підсилюється підсилювачем до напруги , яка підсилюється підсилювачем до напруги 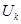 , що подається на двигун, який через редуктор переміщує клапан так, щоб витрата палива змінювалась в таку сторону, щоб компенсувати зміну температури в печі. , що подається на двигун, який через редуктор переміщує клапан так, щоб витрата палива змінювалась в таку сторону, щоб компенсувати зміну температури в печі.
Збурюючою величиною може бути зміна температури навколишнього середовища, теплоємність оточуючого повітря (а значить атмосферного тиску і вологості) та ін. Отже, збурення призводить до порушення теплової рівнноваги й зміні температури в печі. Ця зміна температури приводить до зміни опору терморезистора й розбалансу мосту, який усувається шляхом, аналогічним до випадку зміни задаючої величини.

Рис. 2. Функціональна схема системи автоматичного регулювання температури в печі.
Дана система автоматичного регулювання є звичайною аналоговою лінійною замкнутою стабілізуючою САР з повною початковою інформацією.
У випадку, коли задано диференціальне рівняння елемента системи, його передаточна функція визначається на основі перетворення Лапласа. Для цього вихідне диференціальне рівняння записують у операторній формі та знаходять відношення зображення вихідної величини до зображення вхідної величини при нульових початкових умовах. Якщо елемент системи має дві вхідні величини необхідно визначати дві передаточні функції за кожним із входів. [5, c.6]
Реклама

Нехай диференціальне рівняння об’єкта керування має вигляд
 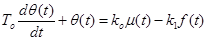 , /2.1/ , /2.1/
де 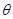 - вихідна величина; - вихідна величина; 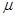 i i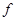 - регулююча і збурююча дії. Знак мінус показує, що зі зростанням навантаження на об’єкт, регульована величина зменшується. - регулююча і збурююча дії. Знак мінус показує, що зі зростанням навантаження на об’єкт, регульована величина зменшується.
Покладемо, що вихідна величина має дві складові
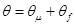 . /2.2/ . /2.2/
Тоді рівняння /1/ розбивається на два рівняння. В операторній формі вони матимуть вигляд
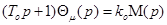 /2.3/ /2.3/
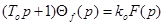 /2.4/ /2.4/
де 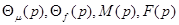 - зображення відповідних величин за Лапласом. - зображення відповідних величин за Лапласом.
Рівнянням /2.3/ і /2.4/ відповідають передаточні функції об’єкта за каналом регулюючої величини
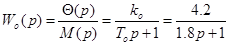 /2.5/ /2.5/
і за каналом збурення
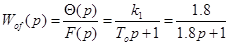 . /2.6/ . /2.6/
Структурна схема об’єкта приведена на рис.3.

Рис.3. Структурна схема об’єкта керування.
Рівняння електричного моста має вигляд
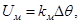 /2.7/ /2.7/
де 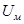 - вихідна величина, напруга на вимірювальній діагоналі моста; - вихідна величина, напруга на вимірювальній діагоналі моста;
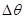 - вхідна величина, відхилення температури в печі від заданого значення. - вхідна величина, відхилення температури в печі від заданого значення.
Тоді рівняння /2.7/ в операторній формі матиме вигляд:
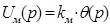 /2.8/ /2.8/
Передаточна функція моста
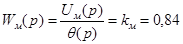 . /2.9/ . /2.9/
Рівняння, що описує роботу підсилювача, має вигляд
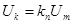 ,/2.10/ ,/2.10/
де 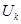 - вихідна величина, - вихідна величина,
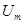 - вхідна величина, - вхідна величина,
kп
- коефіцієнт підсилення.
В операторній формі рівняння /2.10/ запишеться
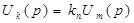 /2.11/ /2.11/
Передаточна функція підсилювача
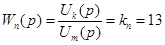 /2.12/ /2.12/
Рівняння, що описує роботу двигуна з редуктором:
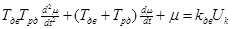 ,/2.13/ ,/2.13/
де 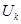 - вхідна величина, - вхідна величина,
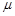 - вихідна величина. - вихідна величина.
Операторна форма рівняння /2.13/:
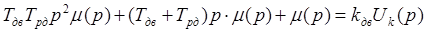 /2.14/ /2.14/
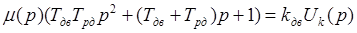 . .
Передаточна функція двигуна з редуктором матиме вигляд
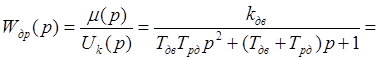
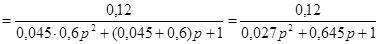 /2.15/ /2.15/
Cтруктурна схема системи автоматичного керування зображена на рис. 4.
 Рис. 4. Структурна схема системи автоматичного регулювання температури в печі.
Для знаходження передаточних функцій системи за каналами задаючої і збурюючої дії користуються правилами еквівалентних перетворень структурних схем. Спочатку, знаходять передаточну функцію розімкнутої системи. Так, як ланки ввімкнені послідовно, то передаточна функція розімкнутої системи знаходиться за формулою
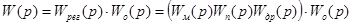 /3.1/ /3.1/
де 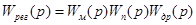 і і 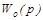 - відповідно предаточні функції регулятора і об’єкта регулювання. - відповідно предаточні функції регулятора і об’єкта регулювання.
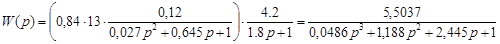 /3.2/ /3.2/
Передаточна функція замкнутої системи за каналом задаючої величини при одиничному зворотному звязку знаходиться через передаточну функцію розімкнутої системи за відомою формулою [3, c.58]
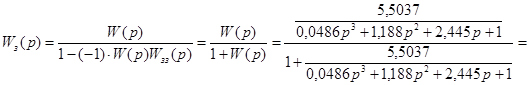
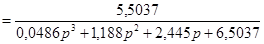 /3.3/ /3.3/
Передаточна функція системи за каналом збурення

 /3.4/ /3.4/
де  - передаточна функція каналу збурення об’єкта. - передаточна функція каналу збурення об’єкта.
Диференціальні рівняння руху системи знаходимо, виходячи із означення передаточної функції системи:
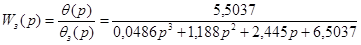 ; ;
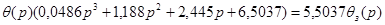 ; ;
Диференціальне рівняння руху системи за каналом завдання-вихід матиме вигляд:
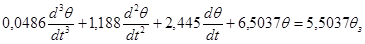 /3.5/ /3.5/
А відповідне рівняння статики:
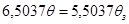 /3.6/ /3.6/
З виразу /3.4/ знаходимо операторну форму диференційного рівняння, яке описує рух системи за каналом збурення-вихід:
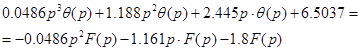 
Виконавши обернене перетворення Лапласа, одержимо:
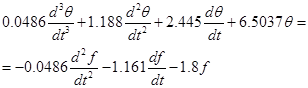 /3.7/ /3.7/
Рівняння статики системи за каналом збурення:
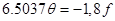 /3.8/ /3.8/
При розробці і настроюванні систем автоматичного керування важливо встановити вплив окремих параметрів на їх стійкість. Для визначення областей допустимих значень параметрів можуть бути використані критерії стійкості та загальний метод D-розбиття.
Зокрема, критичне значення параметру (коефіцієнта передачі 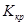 чи постійної часу чи постійної часу 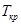 ) при якому система знаходиться на межі області стійкості можна визначити за критерієм Гурвіца. [2, c.131] ) при якому система знаходиться на межі області стійкості можна визначити за критерієм Гурвіца. [2, c.131]
Запишемо характеристичне рівняння системи, передаточна функція якої /3.3/:
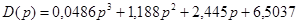 /4.1/ /4.1/
Складемо визначник Гурвіца для даного рівняння:
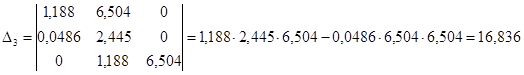 /4.2/ /4.2/
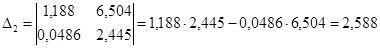 ; ;
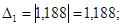
Головний визначник Гурвіца 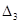 >0 і його мінори >0 і його мінори 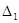 >0, >0, 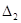 >0, тому система з даними параметрами стійка. >0, тому система з даними параметрами стійка.
Визначення критичного значення коефіцієнта передачі регулятора
Критичне значення коефіцієнта передачі підсилювача знайдемо, прийнявши його за невідомий у виразі /3.2/ та прирівнявши до нуля визначник Гурвіца:
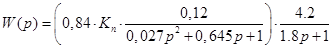 ; ;
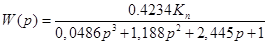 /4.3/ /4.3/
Характеристичне рівняння замкнутої системи
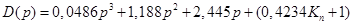 /4.4/ /4.4/
Складемо мінор другого порядку визначника Гурвіца, оскільки він однозначно залежить від значення визначника Гурвіца (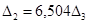 ): ):
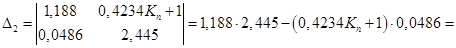
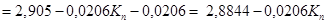 /4.5/ /4.5/
При критичному коефіцієнті передачі 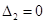 ; ;
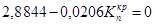 ; ;
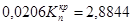 ; ;
 . /4.6/ . /4.6/
Отже, при 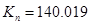 система перебуватиме на межі стійкості. система перебуватиме на межі стійкості.
Для побудови годографа АФЧХ спочатку запишемо передаточну функцію розімкнутої системи /3.2/:
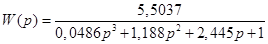 /5.1/ /5.1/
Виконавши заміну p=jω, отримаємо:
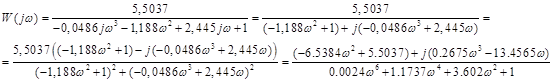
Для побудови годографа в декартовій системі координат виділимо дійсну та уявну частини W (j) =P () +jQ ():
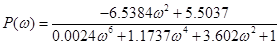 /5.2/ /5.2/
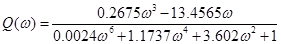 /5.3/ /5.3/
Таблиця значень для побудови годографа АФЧХ
| 0 |
5,5037 |
0 |
| 0,1 |
5,248644 |
-1,29846 |
| 0,2 |
4,574481 |
-2,34665 |
| 0,3 |
3,685451 |
-3,02149 |
| 0,4 |
2,774914 |
-3,34011 |
| 0,5 |
1,960136 |
-3,39168 |
| 0,6 |
1,286218 |
-3,2733 |
| 0,7 |
0,754786 |
-3,06124 |
| 0,8 |
0,348361 |
-2,80676 |
| 0,9 |
0,044273 |
-2,54125 |
| 1 |
-0,17907 |
-2,28258 |
| 1,2 |
-0,45337 |
-1,81802 |
| 1,4 |
-0,58089 |
-1,43841 |
| 1,8 |
-0,6254 |
-0,90382 |
| 2,3 |
-0,54614 |
-0,52005 |
| 3 |
-0,40957 |
-0,25451 |
| 4,5 |
-0,22063 |
-0,0629 |
| 10 |
-0,04472 |
0,009169 |
| 20 |
-0,00761 |
0,005457 |
| 50 |
-0,00036 |
0,000731 |
| 100 |
-2,6E-05 |
0,000106 |

Рис. 5. Годограф амплітудно-фазочастотної характеристики розімкнутої САР.
Запаси стійкості визначимо, виходячи з критерію стійкості Найквіста. [1, с.219] Для визначення запасу стійкості за амплітудою знайдемо частоту, яка відповідає точці перетину годографа АФЧХ з від'ємною дійсною піввіссю (з умови Q (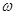 ) =0):
) =0):
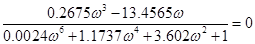 /5.4/ /5.4/
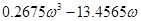 =0 =0
Корені рівняння ω=0; 7.0929; - 7.0929.
Задовольняє умови лише корінь ω=7.0929.
Для даної частоти P (7.0929) =-0,0935.
Запас стійкості по амплітуді Азап
= 1-0,0935=0.9065. /5.5/
Для визначення запасу стійкості за фазою знайдемо критичну частоту ωкр,
при якій А (ω) =1:
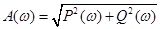
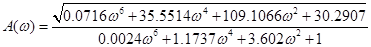 . .
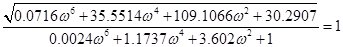 ; ;
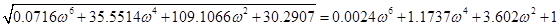 ; ;
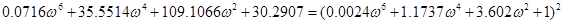 ; ;
Коренями рівняння є:
0 +22.0581j
0 - 22.0581j
0 +22.0295j
0 - 22.0295j
0.0000 + 2.6121j
0.0000 - 2.6121j
1.9187
1.9187
0 + 1.6667j
0 - 1.6667j
0 + 0.5556j
0 - 0.5556j
Серед коренів даного рівняння нас задовольняє лише дійсний додатній корінь, тому ωкр
=1.9187.
P (ωкр
) =Р (1.9187) =-0,613;
Тоді запас стійкості по фазі становить
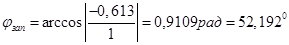 /5.6/ /5.6/
 Рис.6. Графічна ілюстрація запасів стійкості.
Аналітичні методи побудови перехідних характеристик ґрунтуються на розв’язуванні диференціальних рівнянь системи. Найбільш поширеним методом є операторний метод з використанням теореми розкладання.
Зображення вихідної регульованої величини 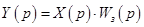
Оскільки перехідна характеристика є реакцією системи на одиничний ступінчастий вхідний сигнал, зображення за Лапласом якого 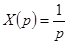 [3, c.29], то [3, c.29], то
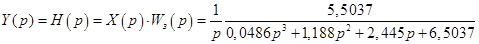 /6.1/ /6.1/
Отже, зображення перехідної функції має вигляд: 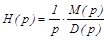 . .
Знайдемо корені характеристичного рівняння замкненої системи D
(p
) = 0:
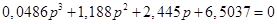 ; /6.2/ ; /6.2/
p1
=-22.4706
p2
=-0.9869 + 2.2319j
p3
=-0.9869 - 2.2319j
У загальному випадку згідно теореми розкладу вираз для перехідної характеристики має вигляд [5, c.12]
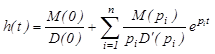 /6.3/ /6.3/
Враховуючи, що при підстановці пари комплексних коренів у вираз /6.3/ значення дробів
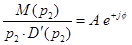 /6.4/ /6.4/
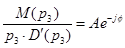
В результаті сума доданків, що відповідають парі комплексно-спряжених коренів може бути зведена, з врахуванням формули Ейлера, до одного виразу:
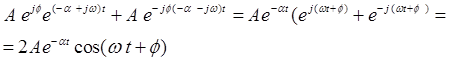 /6.5/ /6.5/
Тоді вираз перехідної функції матиме вигляд
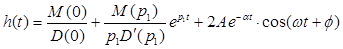 /6.6/ /6.6/
де 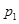 - дійсний корінь характеристичного рівняння /6.2/; - дійсний корінь характеристичного рівняння /6.2/; 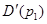 - похідна від полінома знаменника передаточної функції; - похідна від полінома знаменника передаточної функції; 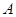 і і 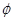 - відповідно дійсна та уявнf частини пари комплексних чисел - відповідно дійсна та уявнf частини пари комплексних чисел 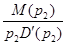 , , 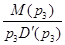 , α і ω - відповідно дійсна та уявна частини пари комплексно-спряжених коренів p2
,p3. , α і ω - відповідно дійсна та уявна частини пари комплексно-спряжених коренів p2
,p3.
M (p) =5.5037;
D (p
) =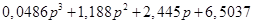 ; ;
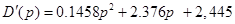 ; ;
Підрахуємо:
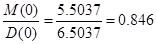 ; /6.7/ ; /6.7/
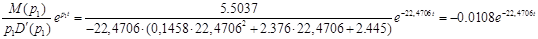
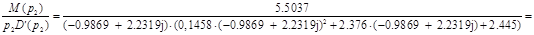 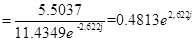 ; /6.8/ ; /6.8/
Відповідно
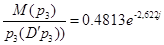 . /6.9/ . /6.9/
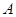 =0,4813; =0,4813;
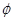 =2,622; =2,622;
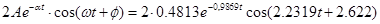 . .
Підставивши у /6.6/, отримаємо рівняння перехідної характеристики:
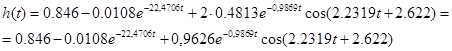 /6.10/ /6.10/
Для графічної побудови перехідної характеристики обчислимо значення h (t) в точках:
| t |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
1,5 |
2 |
| h (t) |
-0,00036 |
0,057818 |
0,242 |
0,482572 |
0,714802 |
0,896603 |
1,054382 |
0,938921 |
| t |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
| h (t) |
0,818175 |
0,79644 |
0,829785 |
0,855775 |
0,857287 |
0,848411 |
| t |
5,5 |
6 |
6,5 |
7 |
| h (t) |
0,843086 |
0,843538 |
0,845765 |
0,846792 |

Рис.7. Перехідна характеристика системи за каналом завдання

Рис. 8. Схема моделювання перехідних процесів системи автоматичного регулювання температури в печі у програмі SIAM.
Для моделювання перехідних процесів у системі автоматичного регулювання була побудована схема (рис.8), у якій задані наступні параметри моделі:
Задані параметри ланок:
K=1
K=0.84
K=13
Перехід від однієї форми передаточної функції коливної ланки
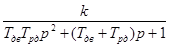
до іншої
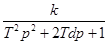
здійснюється за формулами:
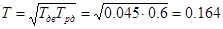 ; ;
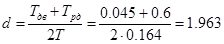 . .
K=0.12
T=0.164
d=1.963
K=4.2
T=1.8
Метод моделювання: Фельберга.
Похибка: 0,001.
Початкове значення часу: 0.
Кінцеве значення часу: 7.
Результати моделювання в СИАМ показані на рис. 9.

Рис. 9. Перехідна характеристика, отримана в результаті моделювання в програмі SIAM.

Порівняємо отримані за допомогою моделювання результати із розрахованими за теоремою розкладу
| t |
0,000 |
0,212 |
0,424 |
0,636 |
0,848 |
1,061 |
| h (t) СИАМ
|
0,0000 |
0,0660 |
0,2690 |
0,5270 |
0,7650 |
0,9380 |
| h (t) розраховане
|
-0,00036 |
0,0660 |
0,2693 |
0,5265 |
0,7641 |
0,9386 |
| δ,% |
- |
0,075 |
0,130 |
0,089 |
0,117 |
0,064 |
| t |
1,414 |
1,626 |
1,980 |
2,404 |
2,616 |
3,040 |
| h (t) СИАМ
|
1,0550 |
1,0390 |
0,9450 |
0,8340 |
0,8050 |
0,7980 |
| h (t) розраховане
|
1,0547 |
1,0393 |
0,9451 |
0,8341 |
0,8045 |
0,7981 |
| δ,% |
0,033 |
0,032 |
0,006 |
0,006 |
0,064 |
0,011 |
| t |
3,535 |
4,030 |
5,020 |
5,515 |
6,505 |
7,000 |
| h (t) СИАМ
|
0,8325 |
0,8567 |
0,8483 |
0,8433 |
0,8460 |
0,8470 |
| h (t) розраховане
|
0,8323 |
0,8565 |
0,8481 |
0,8430 |
0,8458 |
0,8468 |
| δ,% |
0,021 |
0,023 |
0,027 |
0,032 |
0,026 |
0,025 |
Різниця не перевищує 0,13% розрахованого значення h (t), отже результати комп’ютерного моделювання та аналітичного розрахунку практично співпадають.
Іншою комп’ютерною програмою, що дозволяє змоделювати перехідний процес в системі автоматичного регулювання, є система MATLAB, а саме пакет розширення Simulink.
Складена в Simulink модель:

Рис. 10. Схема моделі системи за каналом завдання у програмі Simulink.
В результаті моделювання отримали перехідну характеристику, зображену на рис.11.

Рис. 11. Перехідна характеристика за каналом завдання-вихід, побудована в Simulink.
Якість регулювання оцінюють за допомогою прямих показників якості, котрі визначаються за побудованою перехідною характеристикою досліджуваної системи.
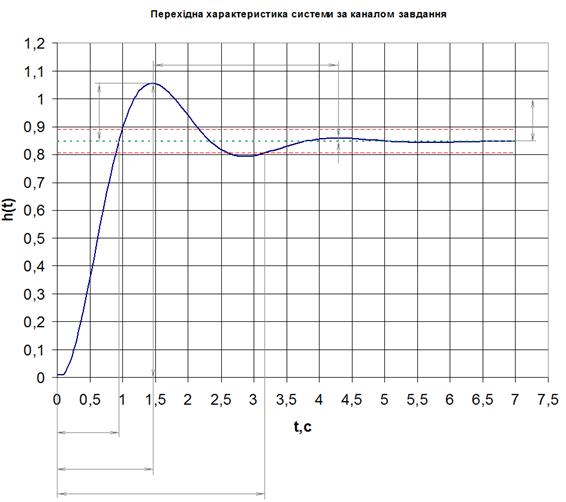 Рис. 12. Знаходження прямих показників якості
tр
=3,2 с - час регулювання
tпу
=0,9 с - час першого досягнення рівня усталеного режиму
tм
=1,4 с - час першого максимуму
δуст
= 0,15 - усталена похибка
hmax
= 1,054 - максимальне значення регульованої величини
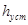 = 0,846 - усталене значення вихідної регульованої величини = 0,846 - усталене значення вихідної регульованої величини
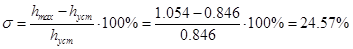 - перерегулювання - перерегулювання
T0
=4.3 c - період коливань
A1
=0, 208
A2
=0,013
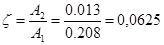 - коливальність - коливальність
Кількість коливань на протязі часу регулювання: N=1
При побудові перехідної характеристики за каналом збурюючої дії приймають задаючий сигнал  =0. Тоді структурну схему системи автоматичного регулювання температури в печі можна предаставити як: =0. Тоді структурну схему системи автоматичного регулювання температури в печі можна предаставити як:
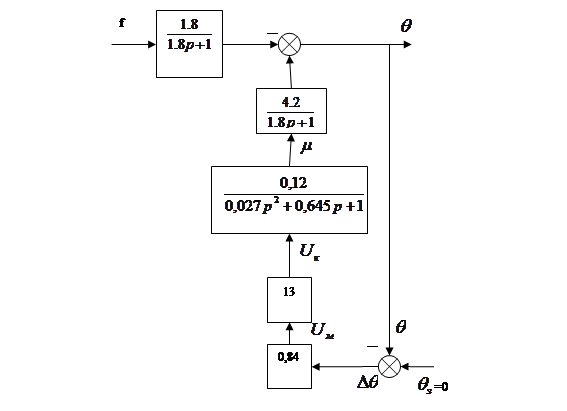
Рис. 13. Структурна схема системи автоматичного регулювання температури в печі.
Для побудови перехідної характеристики за каналом збурення-вихід у Simulink побудована наступна модель:
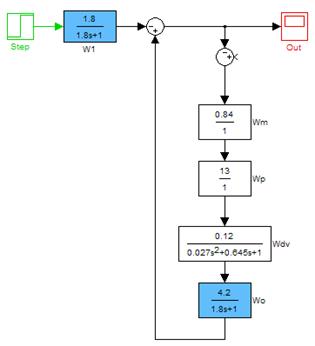
Рис. 14. Схема моделі системи за каналом збурення-вихід у програмі Simulink
В результаті моделювання отримана перехідна характеристика, зображена на рис. 15.
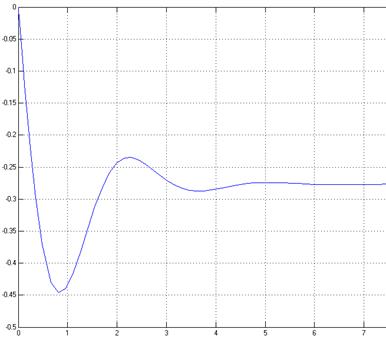
Рис.15. Перехідна характеристика системи за каналом збурюючої дії.
Деякі показники якості системи автоматичного регулювання температури в печі не задовольняють вимогам, що висуваються до якості регулювання такого роду об’єктів, а саме значне перерегулювання та наявність усталеної помилки. Для корекції системи автоматичного регулювання введемо послідовну коректуючу ланку, скористаємось методом Солодовнікова, попередньо задавшись максимально допустимими значеннями:
Бажані показники якості
Час регулювання 2 с
Перерегулювання 5 %
Передаточна функція розімкнутої системи
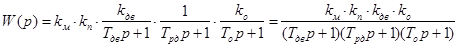 /10.1/ /10.1/
T1
=Tо
=1,8 с;
T2
=Tрд
=0,6 с;
T3
=Tдв
=0,045 с;
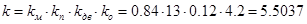 . .
Отже, передаточна функція розімкнутої системи має вигляд
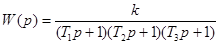 /10.2/ /10.2/
Комплексна передаточна функція розімкнутої системи
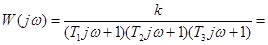 A (ω) ejφ (ω),
де A (ω) ejφ (ω),
де
A (ω) =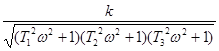 - вираз АЧХ системи. - вираз АЧХ системи.
Логарифмічна частотна характеристика системи описуватиметься виразом
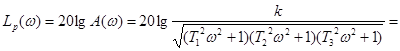
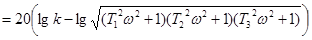 . /10.3/ . /10.3/
Підставивши числові значення, отримаємо:
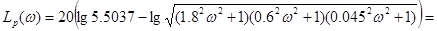
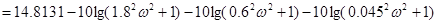 . /10.4/ . /10.4/
Мінімальна величина частоти зрізу:
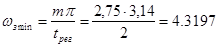 Гц, Гц,
де m=2.75 - знаходимо за номограмою;
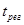 - бажаний час регулювання. - бажаний час регулювання.
Приймаємо частоту зрізу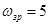 Гц. Гц.
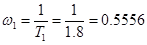 Гц; Гц;
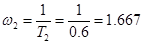 Гц; Гц;
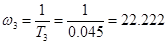 Гц. Гц.
Низькочастотна ділянка бажаної ЛАЧХ характеризує точність роботи в усталеному режимі й визначається порядком астатизму системи та коефіцієнтом передачі системи [1, c.330] та для статичної системи є горизональним променем, що починається при 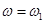 та прямує в напрямку та прямує в напрямку 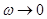 , із ординатою , із ординатою
Lб
=20lg k,/10.5/
де k-коефіцієнт передачі розімкнутої системи.
Для задовільної якості перехідного процесу нахил середньочастотної ділянки бажаної ЛАЧХ повинен бути - 20 дб/дек [1, c.331]. Тому її рівняння повинне мати вигляд
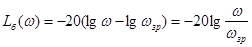 , де , де 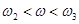 /10.6/ /10.6/
Низькочастотну та середньочастотну ділянки бажаної ЛАЧХ з’єднуємо прямою, що проходить через дві точки: (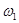 ; 20lg k) та ( ; 20lg k) та (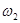 ; ; 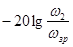 ). Її рівняння матиме вигляд: ). Її рівняння матиме вигляд:
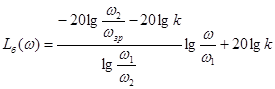 , де , де 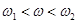 /10.7/ /10.7/
Високочастотна ділянка ЛАЧХ визначає поведінку системи в зоні від’ємних децибелів, а тому впливає тільки на початок перехідного процесу. Щоб збільшити стійкість системи до високочастотних завад, необхідно мати якомога більший (по модулю) нахил ЛАЧХ. [1, c.331] Приймаємо нахил бажаної ЛАЧХ на цій ділянці рівним - 40 дб/дек. Рівняння високочастотної частини ЛАЧХ запишеться
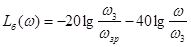 , де , де 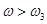 /10.8/ /10.8/
За рівняннями для дійсної /10.4/ та бажаної ЛАЧХ /10.5/, /10.6/, /10.7/, /10.8/ будуємо згадані логарифмічні амплітудно-частотні характеристики в одній системі координат (рис. 15).
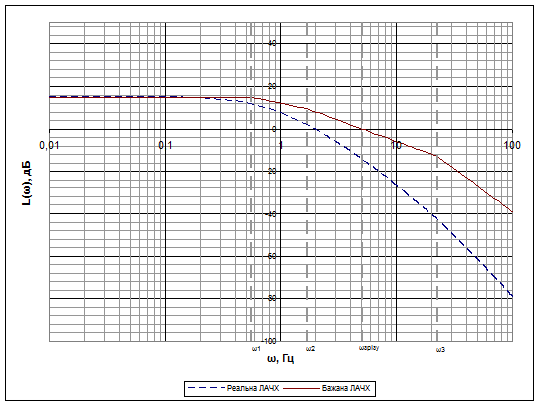
Рис. 15. Реальна та бажана логарифмічні ампілтудо-частотні характеристики.
При послідовному з'єднанні ланок зв'язок між ЛАЧХ ланок наступний:
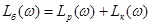 . .
Тоді 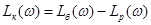 і отримаємо ЛАЧХ коректуючої ланки, представлену на рис. 16. і отримаємо ЛАЧХ коректуючої ланки, представлену на рис. 16.
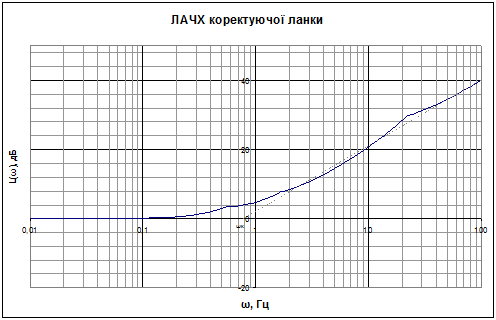
Рис.16. ЛАЧХ коректуючої ланки.
У першому наближенні таку ЛАЧХ має ланка з передаточною функцією
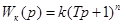 /10.9/ /10.9/
Апроксимуючи отриману ЛАЧХ коректуючої ланки відрізками прямих, знаходимо частоту спряження ωк
=0,7815 Гц; тоді стала часу
Тк
= (ωк
) - 1
=1,2796 с.
Нахил ЛАЧХ коректуючої ланки близький до 20 дб/дек, тому показник степеня /10.9/ дорівнює n=1.
Отже, передаточна функція коректуючої ланки
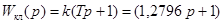 /10.10/ /10.10/
Передаточна функція розімкнутої системи із послідовною коректуючою ланкою
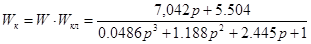 . .
Передаточна функція замкнутої системи із послідовною коректуючою ланкою
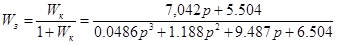 . .
Перехідна характеристика замкнутої системи зображена на рис.17, а годограф АФЧХ розімкнутої системи - на рис. 18.
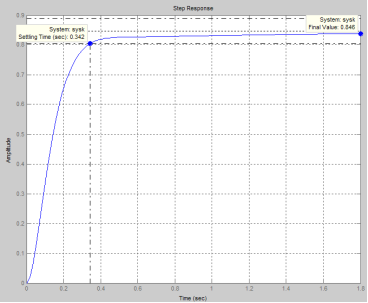
Рис. 17. Перехідна характеристика замкненої системи з послідовною коректуючою ланкою за каналом завдання.
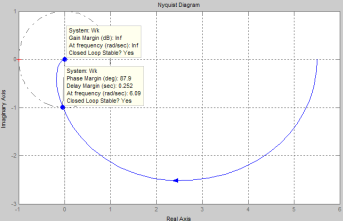
Рис. 18. Годограф АФЧХ розімкнутої системи з послідовною коректуючою ланкою
Отже, введення послідовної коректуючої ланки дозволило зменшити час регулювання з 3,2 с до 0,342 с, усунути перерегулювання, збільшити запас стійкості системи по фазі з 52,20 до 87,90
, проте усталена помилка залишилась на рівні δуст
= 0,15.
Щоб усунути усталену помилку, ввдемо неодиничний зворотній зв’язок із коефіцієнтом передачі kзз
=1-1/kр [
1, с.313], де kр
- коефіцієнт передачі розімкнутої системи.
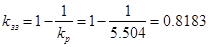 . /10.11/ . /10.11/
Тоді структурна схема системи автоматичного регулювання температури в печі матиме вигляд (рис. 19):

Рис. 19. Структурна схема системи автоматичного регулювання температури в печі після проведення коригування.
Тоді передаточна функція замкнутої системи за каналом завдання матиме вигляд
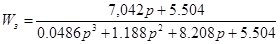 /10.12/ /10.12/
Перехідна характеристика скоректованої системи автоматичного регулювання температури в печі має вигляд, зображений на рис. 20.
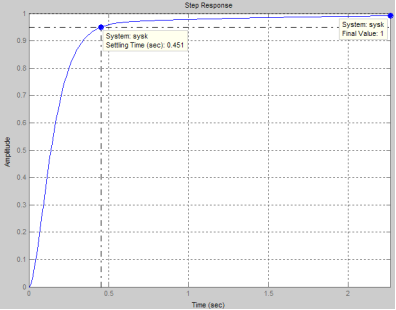
Рис. 20. Перехідна характеристика скоректованої системи за каналом завдання.
Отже, в результаті коригування досягли покращення статичних та динамічних показників якості системи:
| Властивості системи автоматичного регулювання температури в печі |
| Параметр |
Система |
| до коригування |
скорегована |
| Статичні властивості системи |
| Усталена помилка |
0,15 |
0 |
| Динамічні властивості системи |
| Час регулювання |
3,2 с |
0,451 с |
| Перерегулювання |
24.57% |
0 |
| Кількість коливань на протязі часу регулювання |
N=1 |
0 |
| Коливальність |
 |
- |
| Запас стійкості за фазою |
52, 20 |
87,90
|
В ході виконання курсової роботи повели аналіз системи автоматичного регулювання температури в печі: виходячи з рівнянь, що описують динаміку системи та є аналітичними математичними моделями елементів системи, записали передаточні функції елементів системи, розімкнутої системи та замкнутої системи (за каналами завдання-вихід та збурення-вихід). На основі отриманої моделі системи автоматичного регулювання визначили стійкість системи, запаси стійкості, критичне значення коефіцієнта підсилення підсилювача, при якому система перебуватиме на межі стійкості, дослідили реакцію системи на одиничну ступінчасту зміну завдання аналітично за теоремою розкладу, а також шляхом комп’ютерного моделювання, що дозволило оцінити прямі показники якості роботи досліджуваної системи автоматичного регулювання. В результаті дійшли висновку, що дана система автоматичного регулювання температури в печі не задовольняє вимогам, що ставляться до систем того роду, тому була проведена корекція системи шляхом введення послідовної коректуючої ланки та неодиничного зворотного зв’язку. Скорегована система задовольняє нас за своїми якісними показниками та придатна до експлуатації.
1. М.Г. Попович, О.В. Ковальчук. Теорія автоматичного керування: Підручник. - 2-ге вид. - К.: Либідь, 2007. - 656 с.
2. Воронов А.А. Основы теории автоматического управления: Автоматическое регулирование непрерывных линейных систем. - 2-е изд., - М.: Энергия, 1980. - 312 с.
3. Ким Д.П. Теория автоматического управления. Т1. Линейные системы. - М.: ФИЗМАТЛИТ, 2003. - 288 с.
4. Я.З. Цыпкин. Основы теории автоматических систем. Главная редакция физико-математической литературы изд-ва "Наука", М., 1977. - 560 с.
5. Методичні вказівки та завдання на курсову роботу з курсу “Теорія автоматичного керування" для студентів спеціальності 6.092500 “Автоматизоване управління технологічними процесами" /, М.І. Клепач - Рівне: РДТУ, 2002, - 19с.
|