Абсолютная система измерения физических величин
В последние два столетия в науке происходила бурная дифференциация научных дисциплин. В физике помимо классической динамики Ньютона появились электродинамика, аэродинамика, гидродинамика, термодинамика, физика различных агрегатных состояний, специальная и общая теории относительности, квантовая механика и многое другое. Произошла узкая специализация. Физики перестали понимать друг друга. Теорию суперструн, например, понимают лишь насколько сот человек во всем мире. Чтобы профессионально разбираться в теории суперструн, нужно заниматься только теорией суперструн, на остальное просто не хватит времени.
Но не следует забывать, что столь разные научные дисциплины изучают одну и ту же физическую реальность – материю. Наука, а особенно физика, вплотную подошла к тому рубежу, когда дальнейшее развитие возможно только путем интегрирования (синтеза) различных научных направлений. Рассматриваемая абсолютная система измерения физических величин – первый шаг в этом направлении.
В отличие от международной системы единиц СИ, имеющей 7 основных и 2 дополнительные единицы измерения, в абсолютной системе единиц измерения используется одна единица – метр (см. табл.). Переход к размерностям абсолютной системы измерения осуществляется по правилам:
 (1.1)
 (1.2)
Где: L, T и М – размерности длины, времени и массы соответственно в системе СИ.
Физическая сущность преобразований (1.1) и (1.2) состоит в том, что (1.1) отражает диалектическое единство пространства и времени, а из (1.2) следует, что массу можно измерять в квадратных метрах. Правда,  в (1.2) – это не квадратные метры нашего трехмерного пространства, а квадратные метры двумерного пространства. Двумерное пространство получается из трехмерного, если трехмерное пространство разогнать до скорости, близкой к скорости света. Согласно специальной теории относительности, из-за сокращения линейных размеров в направлении движения, куб превратится в плоскость.
Размерности всех остальных физических величин установлены на основании так называемой «пи-теоремы», утверждающей, что любая верная зависимость между физическими величинами с точностью до постоянного безразмерного множителя соответствует какому-либо физическому закону.
Чтобы ввести новую размерность какой-либо физической величины, нужно:
• подобрать формулу, содержащую эту величину, в которой размерности всех других величин известны;
• алгебраически найти из формулы выражение этой величины;
• в полученное выражение подставить известные размерности физических величин;
• выполнить требуемые алгебраические действия над размерностями;
• принять полученный результат как искомую размерность.
«Пи-теорема» позволяет не только устанавливать размерности физических величин, но и выводить физические законы. Рассмотрим для примера задачу о гравитационной неустойчивости среды.
Известно, что как только длина волны звукового возмущения оказывается больше некоторого критического значения, силы упругости (давление газа) не в состоянии вернуть частицы среды в первоначальное состояние. Требуется установить зависимость между физическими величинами.
Имеем физические величины:
•  - длина фрагментов, на которые распадается однородная бесконечно протяженная среда;
•  - плотность среды;
• a - скорость звука в среде;
• G - гравитационная постоянная.
В системе СИ физические величины будут иметь размерность:
~ L ; ~  ; a~ ; G ~ 
Из   , и  составляем безразмерный комплекс:
 ,
где:  и  - неизвестные показатели степеней.
Таким образом:
Так как П по определению величина безразмерная, то получаем систему уравнений:
Решением системы будет:
 ;  ,
следовательно,
Откуда находим:
 (1.3)
Формула (1.3) с точностью до постоянного безразмерного множителя описывает известный критерий Джинса. В точной формуле  .
Формула (1.3) удовлетворяет размерностям абсолютной системы измерения физических величин. Действительно, входящие в (1.3) физические величины имеют размерности:
~  ; ~  ; ~ ; ~ 
Подставив размерности абсолютной системы в (1.3), получим:
Анализ абсолютной системы измерения физических величин показывает, что механическая сила, постоянная Планка, электрическое напряжение и энтропия имеют одинаковую размерность:  . Это означает, что законы механики, квантовой механики, электродинамики и термодинамики – инвариантны.
Например, второй закон Ньютона и закон Ома для участка электрической цепи имеют одинаковую формальную запись:
 ~  (1.4)
 ~ (1.5)
При больших скоростях движения во второй закон Ньютона (1.4) вводится переменный безразмерный множитель специальной теории относительности:
Если такой же множитель ввести в закон Ома (1.5) , то получим:
 (1.6)
Согласно (1,6) закон Ома допускает появление сверхпроводимости, так как 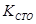 при низких температурах может принимать значение, близкое к нулю. Если бы физика с самого начала применяла абсолютную систему измерения физических величин, то явление сверхпроводимости было бы предсказано вначале теоретически, а уже потом обнаружено экспериментально, а не наоборот.
Много разговоров ведется об ускоренном расширении Вселенной. Замерить ускорение расширения современные технические средства не могут. Применим для решения этой задачи абсолютную систему измерения физических величин.
Вполне естественно предположить, что ускорение расширения Вселенной зависит от расстояния между космическими объектами  и от скорости расширения Вселенной  . Решение задачи изложенным выше методом дает формулу:
 (1.7)
Анализ физического смысла формулы (1.7) выходит за рамки обсуждаемой проблемы. Скажем лишь, что в точной формуле  .
Инвариантность физических законов позволяет уточнить физическую сущность многих физических понятий. Одно из таких «темных» понятий – понятие энтропия. В термодинамике механическому ускорению ~ соответствует массовая плотность энтропии
 ~ ,
где: S – энтропия;
m – масса системы.
Полученное выражение свидетельствует о том, что энтропию, вопреки существующему заблуждению, можно не только вычислить, но и измерить. Рассмотрим для примера металлическую спиральную пружину, которую можно считать механической системой атомов кристаллической решетки металла. Если сжать пружину, то кристаллическая решетка деформируется и создаст силы упругости, которые всегда можно измерить. Сила упругости пружины будет той самой механической энтропией. Если энтропию разделить на массу пружины, то получим массовую плотность энтропии пружины, как системы атомов кристаллической решетки.
Пружину можно представить и одним из элементов гравитационной системы, вторым элементом которой является наша Земля. Гравитационной энтропией такой системы будет сила притяжения, которую можно измерить несколькими способами. Разделив силу притяжения на массу пружины, получим гравитационную плотность энтропии. Гравитационная плотность энтропии – это ускорение свободного падения.
Наконец, в соответствии с размерностями физических величин в абсолютной системе измерения, энтропия газа – это сила, с которой газ давит на стенки сосуда, в который он заключен. Удельная газовая энтропия – это просто давление газа.
Важные сведения о внутреннем устройстве элементарных частиц можно получить, исходя из инвариантности законов электродинамики и аэро-гидродинамики, а инвариантность законов термодинамики и теории информации позволяет наполнить физическим содержанием уравнения теории информации.
Абсолютная система измерения физических величин опровергает широко распространенное заблуждение об инвариантности закона Кулона и закона всемирного тяготения. Размерность массы  ~ не совпадает с размерностью электрического заряда q ~ , поэтому закон всемирного притяжения описывает взаимодействие двух сфер, или материальных точек, а закон кулона описывает взаимодействие двух проводников с током, или окружностей.
Используя абсолютную систему измерения физических величин, мы можем чисто формально вывести знаменитую формулу Эйнштейна:
 ~  (1.8)
Между специальной теорией относительности и квантовой теорией нет непреодолимой пропасти. Формулу Планка можно получить тоже чисто формально:
 ~ (1.9)
Можно и далее демонстрировать инвариантность законов механики, электродинамики, термодинамики и квантовой механики, но рассмотренных примеров достаточно для того, чтобы понять, что все физические законы являются частными случаями некоторых общих законов пространственно-временных преобразований. Интересующиеся этими законами найдут их в книге автора « Теория многомерных пространств ». – М.: Ком Книга, 2007.
Таблица
Переход от размерностей международной системы (СИ) к размерностям абсолютной системы (АС) измерения физических величин
1. Основные единицы
| Наименование физической величины |
Размерность в системе |
Название физической величины |
| СИ |
АС |
| 1 |
2 |
3 |
4 |
| Длина |
 |
|
Метр |
| Масса |
|
|
Килограмм |
| Время |
 |
|
Секунда |
| Сила электрического тока |
 |
|
Ампер |
| Термодинамическая температура |
θ |
|
Кельвин |
| Количество вещества |
 |
|
Моль |
| Сила света |
 |
|
Кандела |
2. Дополнительные единицы
| Плоский угол |
 |
 |
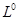Радиан |
| Телесный угол |
|
|
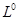Стерадиан |
3. Производные единицы
3.1 Пространственно-временные единицы
| Площадь |
|
|
Квадратный метр |
| Объем |
|
|
Кубический метр |
| Скорость |
 |
|
Метр в секунду |
| Ускорение |
 |
|
Метр на секунду в квадрате |
| Частота |
 |
|
Герц |
| Частота вращения |
|
|
Секунда в минус первой степени |
| Угловая скорость |
|
|
Радиан в секунду |
| Угловое ускорение |
 |
|
Радиан на секунду в квадрате |
3.2 Механические величины
| Плотность |
 |
|
Килограмм на кубический метр |
| Момент инерции |
 |
 |
Килограмм/метр в квадрате |
| Импульс |
 |
|
Килограмм/метр в секунду |
| Момент импульса |
 |
|
Килограмм/метр в квадрате в секунду |
| Сила |
 |
|
Ньютон |
| Момент силы |
 |
 |
Ньютон-метр |
| Импульс силы |
|
|
Ньютон-секунда |
| Давление |
 |
|
Паскаль |
| Поверхностное натяжение |
 |
|
Ньютон на метр |
| Работа, энергия |
|
|
Джоуль |
| Мощность |
 |
 |
Ватт |
| Динамическая вязкость |
 |
|
Паскаль-секунда |
| Кинематическая вязкость |
 |
|
Квадратный метр на секунду |
3.3 Тепловые единицы
| Количество теплоты |
|
|
Джоуль |
| Удельное количество теплоты |
 |
|
Джоуль на килограмм |
| Энтропия и теплоемкость |
 θ -1 |
|
Джоуль на кельвин |
| Теплоемкость удельная |
 θ -1 |
|
Джоуль на килограмм - кельвин |
| Теплоемкость молярная |
L2MT-2N-1θ-1 |
L3 |
Джоуль на моль-кельвин |
| Теплопроводность |
LMT-3N-1θ-1 |
|
Ватт на моль-кельвин |
3.4 Электрические величины
| Плотность электрического тока |
 |
|
Ампер на квадратный метр |
| Электрический заряд |
 |
|
Кулон |
| Плотность электрического заряда линейная |
 |
|
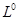Кулон на метр |
| Плотность электрического заряда поверхостная |
 |
|
Кулон на метр квадратный |
| Магнитодвижущая сила |
I |
|
Ампер |
| Напряженность магнитного поля |
L-1 I |
L |
Ампер на метр |
| Индуктивность |
L2 M T -2 I -2 |
L2 |
Генри |
| Магнитная постоянная |
L M T -2 I -2 |
L |
Генри на метр |
| Магнитный момент электрического тока |
L2 I |
L4 |
Ампер – квадратный метр |
| Намагниченность |
L-1 I |
L |
Ампер на метр |
| Магнитное сопротивление |
L-2 M -1T 2 I 2 |
L -2 |
Ампер на вебер |
3.5 Энергетическая фотометрия
| Световой поток |
J |
 |
Люмен |
| Освешенность |
L-2 J |
|
Люкс |
| Поток излучения |
L2 M T-3 |
|
Ватт |
| Энергетическая освещенность и светимость |
M T -3 |
|
Ватт на квадратный метр |
| Энергетическая яркость |
M T -3 |
|
Ватт на стерадиан квадратный метр |
Спектральная плотность энергетической светимости:
• по длине волны
• по частоте
|
L-1 M T -3
M T- -2
|
|
Ватт на м3
Джоуль на м2
|
|
