Об одной общей краевой задаче со смещением для нагруженного уравнения третьего порядка с кратными характеристиками
Кодзодков А.Х.
Кафедра математического анализа.
Кабардино-Балкарский государственный университет
Рассмотрим линейное нагруженное уравнение третьего порядка:
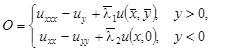 (1) (1)
в – области 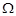 , ограниченной отрезками , ограниченной отрезками 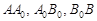 прямых прямых 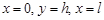 соответственно при соответственно при 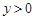 и характеристиками и характеристиками 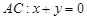 , , 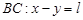 уравнения (1) при уравнения (1) при 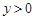 ; ; 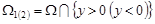 ; ; 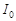 – интервал – интервал 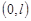 , , 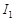 – интервал – интервал 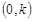 . .
Здесь положено, что:
1) 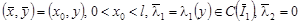
или 2) 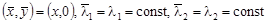 . .
Пусть имеет место случай (1).
Задача 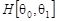 . Найти функцию . Найти функцию 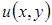 со следующими свойствами: 1) со следующими свойствами: 1) 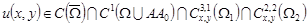 ; ;
2) 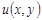 – регулярное решение уравнения (1) при – регулярное решение уравнения (1) при 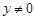 ; ;
3) 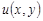 удовлетворяет краевым условиям удовлетворяет краевым условиям
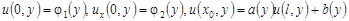 , , 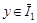 ; (2) ; (2)
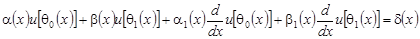 , ,
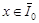 , (3) , (3)
где 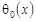 , , 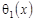 – аффиксы точек пересечения характеристик уравнения (1) при y < 0, выходящих из точки – аффиксы точек пересечения характеристик уравнения (1) при y < 0, выходящих из точки 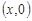 с характеристиками АС и ВС соответственно; с характеристиками АС и ВС соответственно; 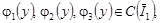 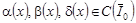 , , 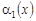 , , 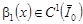 . .
Опираясь на однозначную разрешимость задачи Коши для уравнения (1) при y < 0 с начальными данными 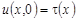 , , 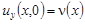 , легко видеть, что если существует решение задачи , легко видеть, что если существует решение задачи 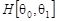 , то оно представимо в виде: , то оно представимо в виде:
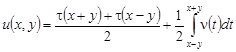 . (4) . (4)
Учитывая (4) в краевом условии (3), получаем:
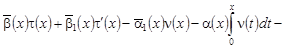
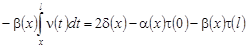 , (5) , (5)
где 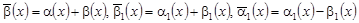 . .
Следуя [1], обозначим через 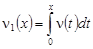 первообразную функции первообразную функции 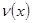 . Тогда уравнение (5) примет вид: . Тогда уравнение (5) примет вид:
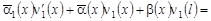
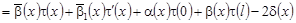 , (6) , (6)
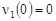 , (7) , (7)
где 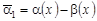 . .
Относительно коэффициентов уравнения (6) будем рассматривать аналогичные ситуации, приведенные в работе [1]:
1) 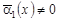 , т.е. , т.е. 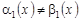 ; ;
2) 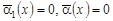 , , т.е. , , т.е. 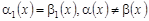 ; ;
3)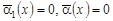 , т.е. , т.е. 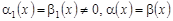 ; ;
4) 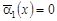 , , 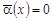 , т.е. , т.е. 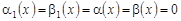 . .
Пусть имеет место случай (1) и функции 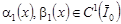 . Решение задачи (6), (7) в этом случае имеет вид: . Решение задачи (6), (7) в этом случае имеет вид:
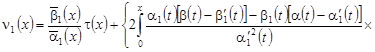
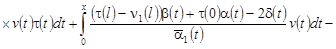
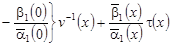 , (8) , (8)
где 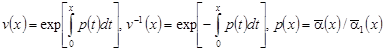 . .
Дифференцируя равенство (8) и делая несложные преобразования, получаем:
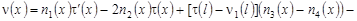
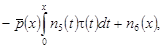 (9) (9)
где 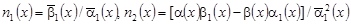 , ,
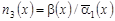 , , 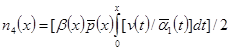 , ,
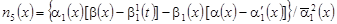 , ,
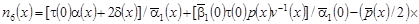
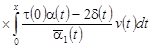 , , 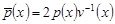 . .
Переходя к пределу в уравнении (1) при 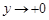 , получаем функциональное соотношение между , получаем функциональное соотношение между 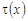 и и 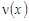 , принесенное из области , принесенное из области 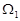 , на линию , на линию 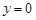 : :
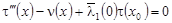 . (10) . (10)
В силу граничных условий (2) и равенства (9) получим нелокальную задачу для нагруженного неоднородного интегро-дифференциального уравнения третьего порядка с переменными коэффициентами:
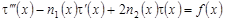 , (11) , (11)
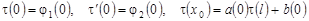 , (12) , (12)
где 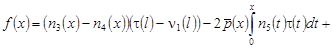
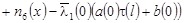 . .
В начале положим, что 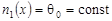 , т.е. , т.е.
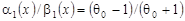 , , 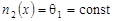 , т.е. , т.е.
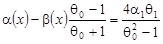 . .
В зависимости от значений корней характеристического уравнения
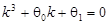 , (13) , (13)
соответствующего однородному уравнению (11) ( ), будем исследовать разрешимость задачи (11), (12). ), будем исследовать разрешимость задачи (11), (12).
Введем обозначение 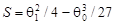 . Логически возможны три различных случая: 1) S>0, 2) S=0, 3) S<0. . Логически возможны три различных случая: 1) S>0, 2) S=0, 3) S<0.
Известно, что [2]: 1) если S>0, то уравнение (13) имеет только один действительный корень, а два остальных корня будут сопряженными чисто комплексными числами; 2) если S=0, то все три корня уравнения (13) действительны, причем два из них равны; 3) если S<0, то все три корня уравнения (13) действительны, причем все они различны.
Реклама

Пусть S=0, т.е. 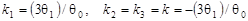 . .
Общее решение уравнения (11) в этом случае имеет вид:
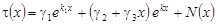 , (14) , (14)
где 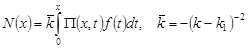 , ,
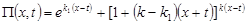 . .
Удовлетворяя (14) граничным условиям (12), получим линейную алгебраическую систему трех уравнений относительно 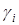 с определителем: с определителем:
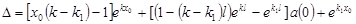 . .
Положим, что 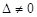 . Тогда . Тогда 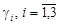 находят по формулам: находят по формулам:
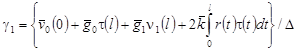 , (15) , (15)
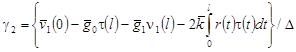 , (16) , (16)
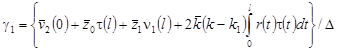 , (17) , (17)
где 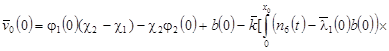
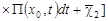 , ,
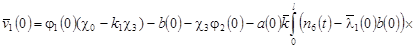
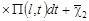 , ,
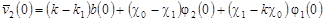 , ,
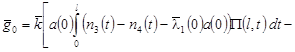
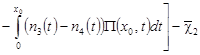 , ,
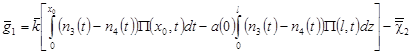 , ,
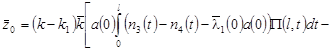
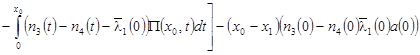 , ,
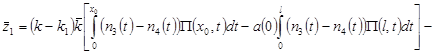 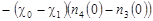 , ,
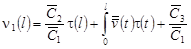 , ,
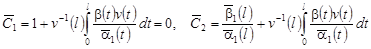 , ,
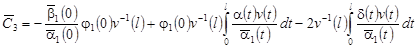 , ,
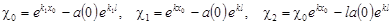 , ,
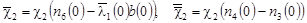 , ,
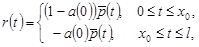
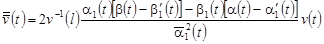 . .
Учитывая (15) – (17) в (14), получаем:
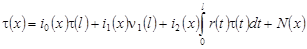 , ,
где 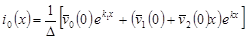 , ,
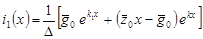 , ,
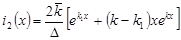 , ,
или
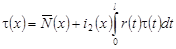 , (18) , (18)
где 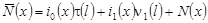 . .
Если считать функцию 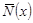 известной, то (18) представляет собой интегральное уравнение Фредгольма второго рода с вырожденным ядром относительно известной, то (18) представляет собой интегральное уравнение Фредгольма второго рода с вырожденным ядром относительно 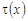 . Обозначив . Обозначив
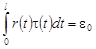 , ,
решение уравнения (18) будем искать в виде:
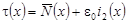 . (19) . (19)
После подстановки (19) в (18) имеем выражение:
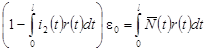 . .
Если 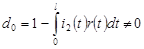 , то , то 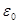 определяется по формуле: определяется по формуле:
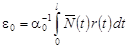 . (20) . (20)
Учитывая (19), (20) в (18), получаем:
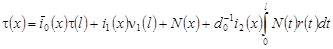 , (21) , (21)
где 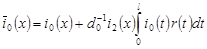 , ,
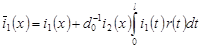 . .
В равенстве (21) учтем значение 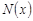 . В результате будем иметь: . В результате будем иметь:

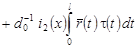 , (22) , (22)
где 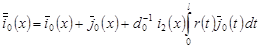 , ,
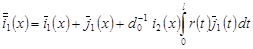 , ,
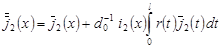 , ,
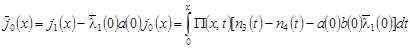 , ,
 , ,
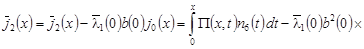
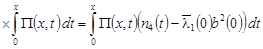
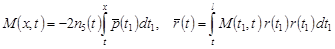 . .
Перепишем уравнение (22) в виде:
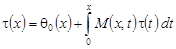 , (23) , (23)
где 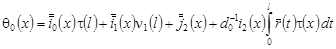 . .
В силу условий, наложенных на заданные функции 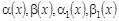 , можем заключить, что , можем заключить, что 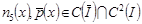 , следовательно , следовательно 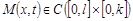 . .
Обращая интегральное уравнение Вольтерра второго рода (23), получаем:
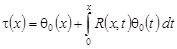 , (24) , (24)
где 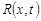 – резольвента ядра – резольвента ядра 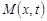 . Заметим, что резольвента . Заметим, что резольвента 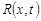 обладает такими же свойствами, что и ядро обладает такими же свойствами, что и ядро 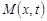 [3]. [3].
Заменяя в равенстве (24) функцию 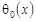 ее значением, получаем: ее значением, получаем:
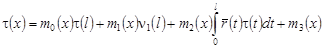 , (25) , (25)
где 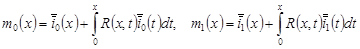 , ,
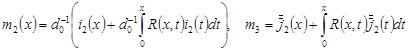 . .
Перепишем уравнение (25) в виде:
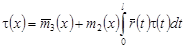 , (26) , (26)
где 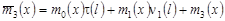 . .
Решение уравнения (26) будем искать в виде:
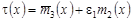 , (27) , (27)
где 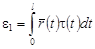 . .
Поступая аналогично предыдущему случаю, получим
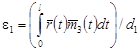 , если , если 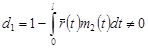 . .
Таким образом, имеем:
| 3 Труды молодых ученых № 3, 2007 |
|
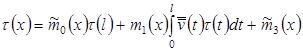 , (28) , (28)где 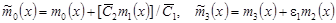 . .
Уравнение (28) перепишем в виде:
 , (29) , (29)
где  . .
Решение уравнения (29) ищем в виде:
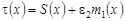 , (30) , (30)
где 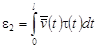 . .
Подберем теперь постоянную 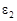 так, чтобы определенная формулой (30) функция так, чтобы определенная формулой (30) функция 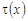 была решением интегрального уравнения (29). С этой целью внесем выражение (30) для была решением интегрального уравнения (29). С этой целью внесем выражение (30) для 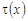 в левую часть (29). После простых вычислений получаем: в левую часть (29). После простых вычислений получаем:
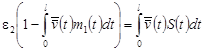 , ,
откуда
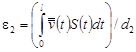 , ,
где положено, что
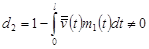 . .
Таким образом, имеем:
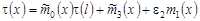 . (31) . (31)
Полагая в равенстве 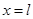 , находим , находим
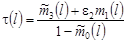 , ,
если 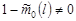 , т.е. , т.е.
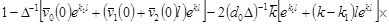
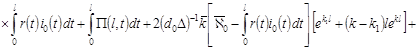
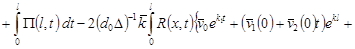
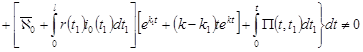 . .
Пусть теперь имеет место случай 2), причем :
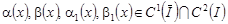 . .
В этом случае уравнение (6) принимает вид:
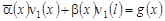 , (32) , (32)
где 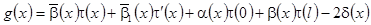 . .
Учитывая условие (7), из (32) получаем соотношение 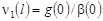 , , 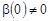 . Подставляя это значение в (32), находим . Подставляя это значение в (32), находим
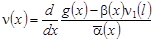 . (33) . (33)
Подставляя (33) в (10), получаем нагруженное уравнение:
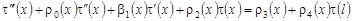 , (34) , (34)
где 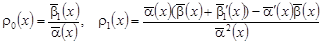 , ,
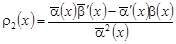 , ,
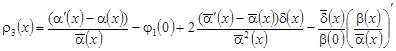 , ,
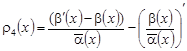
с внутренне-краевыми условиями (12).
Рассмотрим частный случай, когда 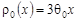 , т.е. , т.е.
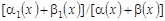 = =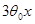 ; ; 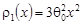 , т.е. , т.е.
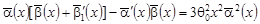 ; ; 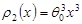 , т.е. , т.е.
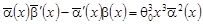 . .
Тогда общее решение однородного уравнения
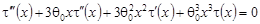 имеет вид [4]: имеет вид [4]:
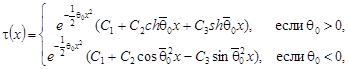
где 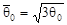 . .
Пусть 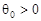 . Методом вариации постоянных находим общее решение неоднородного уравнения (34) в виде: . Методом вариации постоянных находим общее решение неоднородного уравнения (34) в виде:
Реклама

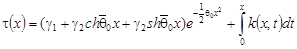 , (35) , (35)
где 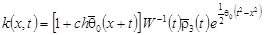 , ,
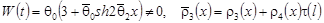 . .
Удовлетворяя (35) условиям (12), получаем:
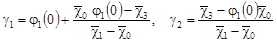 , ,
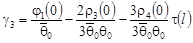 , ,
где
 , ,
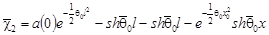 , ,
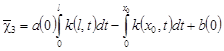 , причем выполняется условие , причем выполняется условие
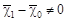 , т.е. , т.е. 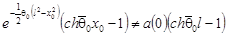 . .
Равенство (35) перепишем в виде:
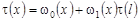 , (36) , (36)
где 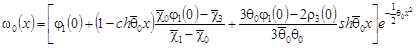 , , 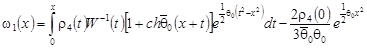 . .
Из (36) при 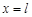 , имеем , имеем
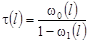 , ,
если выполняется условие 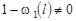 , т.е. , т.е.
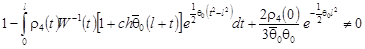 . .
Пусть имеет место случай 3), причем 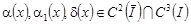 , , 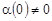 . Тогда уравнение (6) принимает вид [1]: . Тогда уравнение (6) принимает вид [1]:
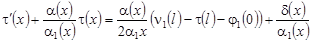 . (37) . (37)
Полагая в равенстве (37) 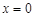 и, учитывая условия и, учитывая условия 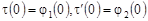 , получим: , получим:
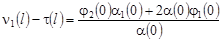 . .
Следовательно, для 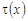 имеем представление имеем представление
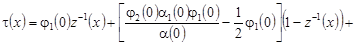
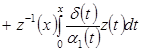 , (38) , (38)
где 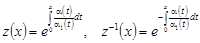 . .
Если выполняется условие 4) и функции 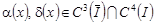 , причем , причем 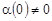 , то имеем равенство , то имеем равенство
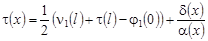 . (39) . (39)
Полагая в равенстве (39) 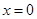 и, учитывая условие и, учитывая условие 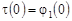 , находим , находим
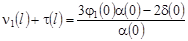 . .
Таким образом, имеем, что
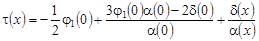 . (40) . (40)
Полагая в равенствах (38), (40) 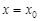 , найдем , найдем 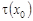 , а затем, подставляя их в равенство (10), однозначно найдем неизвестную функцию , а затем, подставляя их в равенство (10), однозначно найдем неизвестную функцию 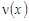 . .
Случай 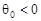 исследуется аналогично. исследуется аналогично.
После определения функций 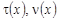 решение задачи решение задачи 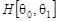 в области в области 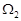 задается формулой (4), а в области задается формулой (4), а в области 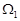 приходим к задаче (1), (2), приходим к задаче (1), (2), 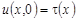 . .
Решение этой задачи дается формулой [5]:
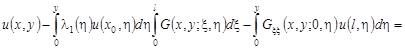
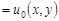 , (41) , (41)
где 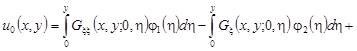
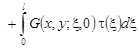 . .
Отсюда, полагая в равенстве (41) 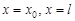 , получаем систему интегральных уравнений типа Вольтерра второго рода: , получаем систему интегральных уравнений типа Вольтерра второго рода:
 (42) (42)
где 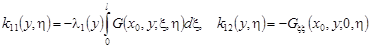 , ,
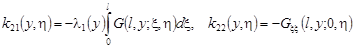 . .
В силу свойств функции 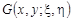 и ядер системы (42), нетрудно убедиться, что система уравнений (42) допускает единственное решение в пространстве и ядер системы (42), нетрудно убедиться, что система уравнений (42) допускает единственное решение в пространстве  [3]. [3].
Список литературы
Наджафов Х.М. Об одной общей краевой задаче со смещением для уравнения Лаврентьева-Бицадзе // Известия КБНЦ РАН. Нальчик, №1(8), 2002.
Фадеев Д.К. Лекции по алгебре. М.1984.
Мюнтц Г. Интегральные уравнения. Л.-М., Т.1, 1934.
Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1971.
Джураев Т.Б. Краевые задачи для уравнений смешанного и смешанно-составного типов. Ташкент: Фан, 1979.
|